中考复习专题——折叠结构问题教案
图片预览


文档简介
折叠结构
【轴对称(折叠)思考层次全貌】
全等变换:对应边相等、对应角相等.
对称轴性质:对称轴上的点到对应点的距离相等,对应点所连线段被对称轴垂直平分.
组合搭配:矩形背景下常出现等腰三角形、两次折叠常出现直角,60°角、折叠会出现圆弧等.
作图:核心是找到对应点,作对应点连线的垂直平分线(折痕),补全图形.
【要求】
①读一读操作要领,按照操作要领去做题,思路受阻时回头再看操作要领,做完题对照操作要领思考一步步是如何进行操作的;
②做题时,需要执行读题标注(如目标、条件),观察特征,验证取舍等动作.
【第一次训练】
操作要领:
遇折叠,考虑全等变换;找折痕(对称轴),利用对应边相等,对应角相等转移条件,表达线段长,利用勾股定理(或相似、三角函数)建方程;做题时常借助背景图形提供的角度、线段长,对条件进行转移、表达.
【例题1】如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则线段CN的长为__________cm.
分析思路:
读题标注、转化;
正方形,折叠,中点,目标,如右图所示
背景图形;
边长为8的正方形;
分析条件,组合特征;
折叠是全等变换----对应边相等,对应角相等;
EN=DN;______+NC=DN+NC=8,
转移,表达----设CN=x,则EN=DN=_____
求解目标:勾股定理列方程
在Rt△______中,勾股定理列方程为_______________,解得x=_______即CN=_____cm.
【配套小练习】
练习1:如图,有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,点D在BC边上,将直角边AC沿直线AD折叠,点C恰好落在斜边AB上的点E处,则线段CD的长为__________.
练习2:如图,折叠长方形的一边AD,使点D落在BC边上的点F处,若AB=4cm,BC=5cm,则EF的长为________.
【第二次训练】
操作要领:
①折叠属于全等变换,找折痕,利用对应边相等,对应角相等转移条件,表达线段长,利用勾股定理建方程;
②上述思路进行不下去时,从“对称轴上的点到对应点的连线距离相等”,从折痕与背景图形的交点处入手,结合所求目标,连接对应线段,表达求解;或者考虑“折痕”为对称轴,“对应点所连线段被对称轴垂直平分”,利用垂直平分(题目中会出现全等或相似)解题.(这两条性质可以逐一尝试)
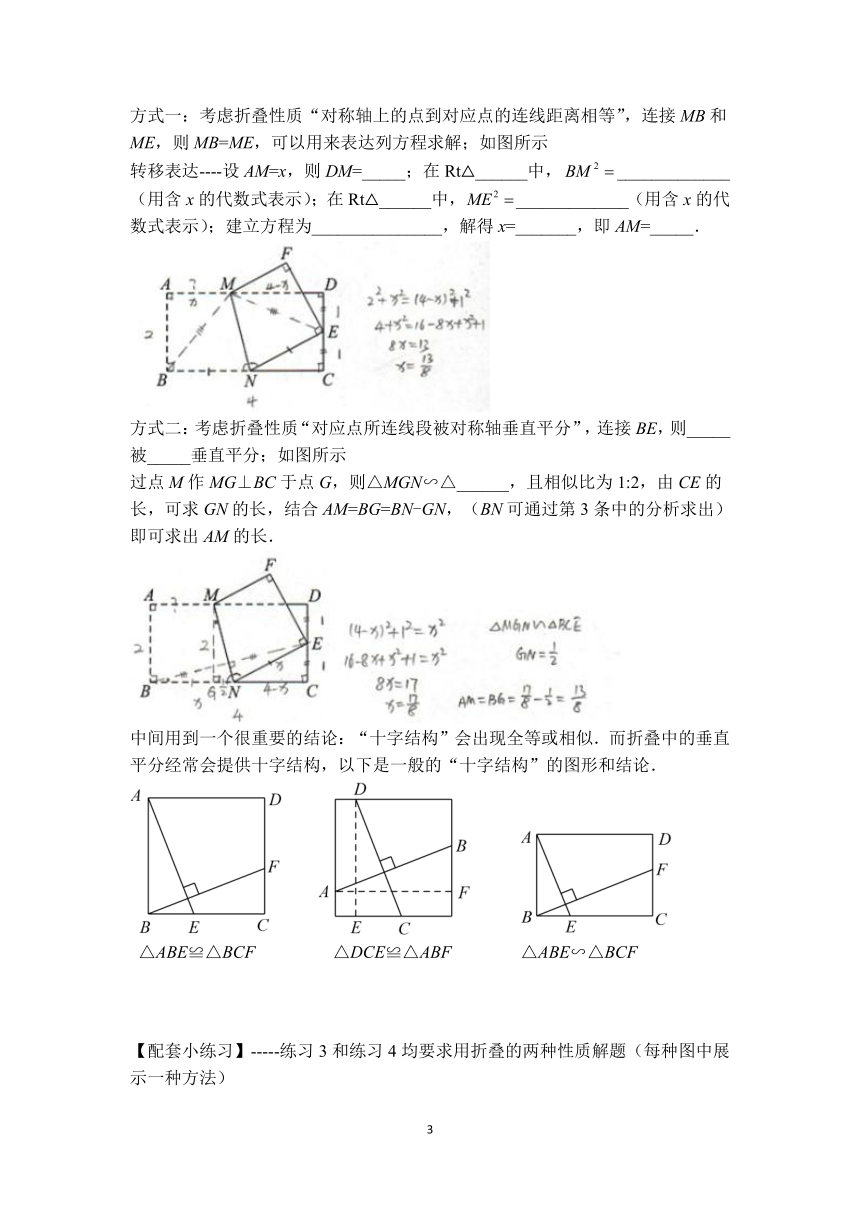
【例题2】如图,将长为4cm,宽为2cm的长方形纸片ABCD折叠,使点B落在CD边的中点E处,压平后得到折痕MN,则线段AM的长为__________.
分析思路:
读题标注、转化;
长方形,折叠,中点,目标,如右图所示
背景图形;
长为4,宽为2的长方形,DE=EC=1,E是定点;
分析条件,组合特征;
折叠是全等变换----对应边相等,对应角相等;
上方:AM=MF,但MF所在的直角三角形无相关线段长信息,求解不出来;
下方:BN=EN;______+NC=BN+NC=4,在Rt△______中,勾股定理能够求BN(NE,NC等),但跟目标无关,先不进行计算;
求解目标;
方式一:考虑折叠性质“对称轴上的点到对应点的连线距离相等”,连接MB和ME,则MB=ME,可以用来表达列方程求解;如图所示
转移表达----设AM=x,则DM=_____;在Rt△______中,_____________(用含x的代数式表示);在Rt△______中,_____________(用含x的代数式表示);建立方程为_______________,解得x=_______,即AM=_____.
方式二:考虑折叠性质“对应点所连线段被对称轴垂直平分”,连接BE,则_____被_____垂直平分;如图所示
过点M作MG⊥BC于点G,则△MGN∽△______,且相似比为1:2,由CE的长,可求GN的长,结合AM=BG=BN-GN,(BN可通过第3条中的分析求出)即可求出AM的长.
中间用到一个很重要的结论:“十字结构”会出现全等或相似.而折叠中的垂直平分经常会提供十字结构,以下是一般的“十字结构”的图形和结论.
△ABE≌△BCF
△DCE≌△ABF
△ABE∽△BCF
【配套小练习】-----练习3和练习4均要求用折叠的两种性质解题(每种图中展示一种方法)
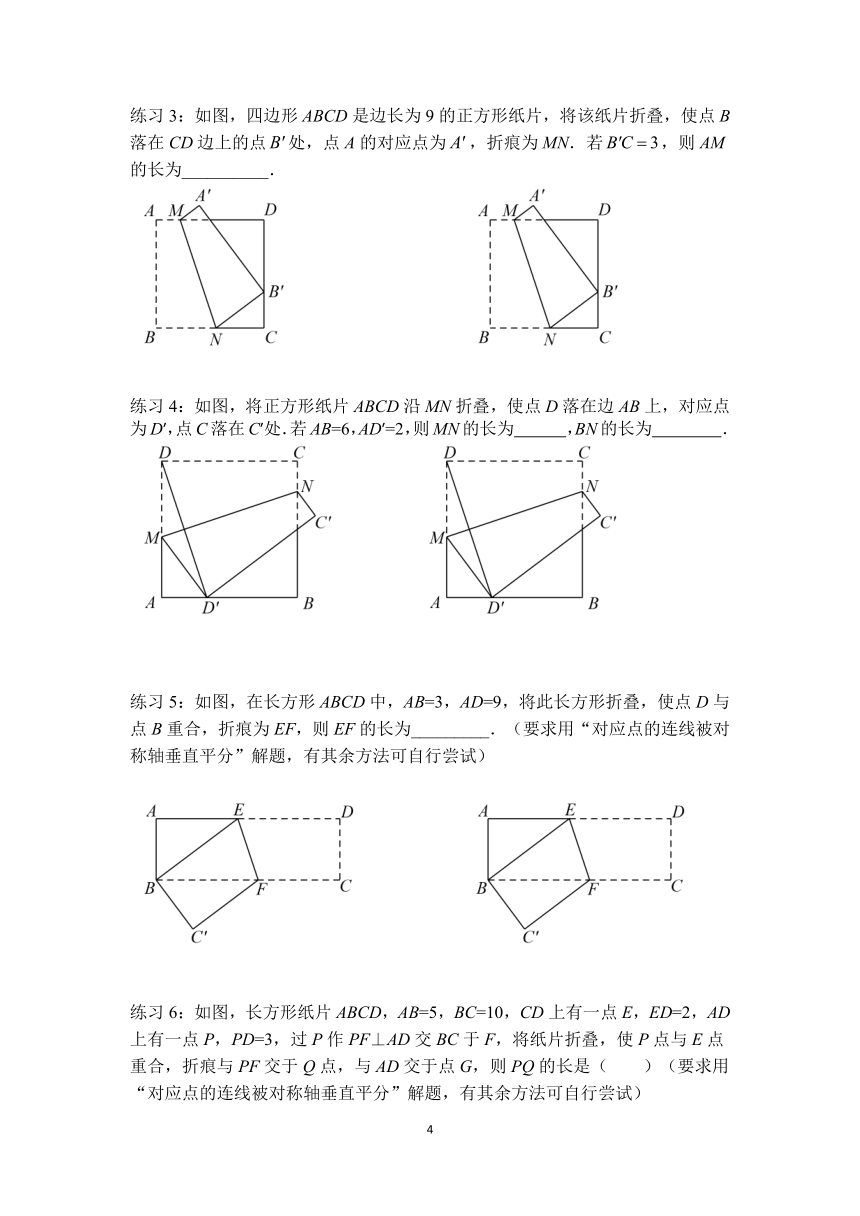
练习3:如图,四边形ABCD是边长为9的正方形纸片,将该纸片折叠,使点B落在CD边上的点处,点A的对应点为,折痕为MN.若,则AM的长为__________.
练习4:如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则MN的长为 ,BN的长为 .
练习5:如图,在长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点D与点B重合,折痕为EF,则EF的长为_________.(要求用“对应点的连线被对称轴垂直平分”解题,有其余方法可自行尝试)
练习6:如图,长方形纸片ABCD,AB=5,BC=10,CD上有一点E,ED=2,AD上有一点P,PD=3,过P作PF⊥AD交BC于F,将纸片折叠,使P点与E点重合,折痕与PF交于Q点,与AD交于点G,则PQ的长是(
)(要求用“对应点的连线被对称轴垂直平分”解题,有其余方法可自行尝试)
A.
B.3
C.
D.
练习7:如图,将边长为12cm的正方形ABCD折叠,使得A点落在边CD上的E点,然后压平得折痕FG,若GF的长为13cm,则线段CE的长为_____________.
【第三次训练】
操作要领:
当上述两种思路都进行不下去的时候考虑背景提供的条件,如长方形中折叠会出现等腰三角形(以折痕为底);(原理是:平行+角平分线出现等腰三角形)
【例题3】用长方形下的折叠会出现等腰三角形,快速求BF的长
如图,在长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点D与点B重合,折痕为EF,则BF的长为_________.
拓展:请在右上图中补全(例题2)长方形下的折叠出现的等腰三角形,在图上进行体现,并用此思路尝试求AM的长;
如图,将长为4cm,宽为2cm的长方形纸片ABCD折叠,使点B落在CD边的中点E处,压平后得到折痕MN,则线段AM的长为__________.
【配套小练习】
练习8:如图,长方形ABCD中,AB=15cm,点E在AD上,且AE=9cm,连接EC,将长方形ABCD沿直线BE翻折,点A恰好落在EC上的点A'处,则A'C=_______cm.
练习9:已知一个长方形纸片OABC,OA=6,点P为AB边上一点,AP=2,将△OAP沿OP折叠,点A落在点A′处,延长PA′交边OC与点D,经过点P再次折叠纸片,使点B落在边OC上的点D处,则AB的长为____________.
练习10:如图,四边形ABCD是边长为9的正方形纸片,将该纸片折叠,使点B落在CD边上的点处,点A的对应点为,折痕为MN.若,则AM的长为__________.(请用长方形下的折叠会出现等腰三角形,解题)
【第四次训练】折叠作图训练及计算求解
题目中给出已知的对应点,直接作垂直平分线,找折痕;
题目中没有直接给出的对应点,而是给出对应点满足的条件;
此时往往“折痕过定点”,题目往往会产生圆(圆弧),通过作圆弧找到对应点的位置,再作垂直平分线找折痕.
练习11:如图,在矩形ABCD中,已知AB=12,AD=8,如果将矩形沿直线l翻折后,点A落在边CD的中点E处,直线l分别与边AB,AD交于点M,N,那么MN的长为_________.
练习12:在矩形ABCD中,AB=4,BC=3,点P在线段AB上.若将△DAP沿DP折叠,使点A落在对角线AC上的A′处,则AP的长为_____________.
练习13:如图,矩形ABCD中,AB=2,AD=6,AF=BE=2,点G是线段AD上的动点,将矩形ABCD沿直线EG折叠.当点C的对应点C′落在四边形ABEF对角线所在直线上时,求AC′的长为_____________.
练习14:如图,矩形纸片ABCD中,AB=8cm,BC=20cm,O是BC的中点,沿过O的直线翻折.若点B恰好落在AD上,那么折痕的长度为________.
练习15:在矩形ABCD中,BC=6,CD=8,点P在线段AB上(不含端点A,B)任意一点.若将△PBC沿PC折叠,使点B的对应点B′落在矩形ABCD对角线上时,BP的长为_____________.
用你学到的内容,尝试用多种方法解题。
如图,矩形ABCD中,AB=12,BC=10,点E是BC上一点且BE=2,点F是CD上一点且CF=4,将矩形ABCD折叠,使点E和点F重合,折痕分别与AD、BC交于点HG,则AH的长为__________.
如图,在矩形ABCD中,AB=10,AD=6,沿过点A的直线折叠矩形ABCD,使得点B落在线段CD上,折痕交CB于点F,则AF=________.
8
【轴对称(折叠)思考层次全貌】
全等变换:对应边相等、对应角相等.
对称轴性质:对称轴上的点到对应点的距离相等,对应点所连线段被对称轴垂直平分.
组合搭配:矩形背景下常出现等腰三角形、两次折叠常出现直角,60°角、折叠会出现圆弧等.
作图:核心是找到对应点,作对应点连线的垂直平分线(折痕),补全图形.
【要求】
①读一读操作要领,按照操作要领去做题,思路受阻时回头再看操作要领,做完题对照操作要领思考一步步是如何进行操作的;
②做题时,需要执行读题标注(如目标、条件),观察特征,验证取舍等动作.
【第一次训练】
操作要领:
遇折叠,考虑全等变换;找折痕(对称轴),利用对应边相等,对应角相等转移条件,表达线段长,利用勾股定理(或相似、三角函数)建方程;做题时常借助背景图形提供的角度、线段长,对条件进行转移、表达.
【例题1】如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在点F处,折痕为MN,则线段CN的长为__________cm.
分析思路:
读题标注、转化;
正方形,折叠,中点,目标,如右图所示
背景图形;
边长为8的正方形;
分析条件,组合特征;
折叠是全等变换----对应边相等,对应角相等;
EN=DN;______+NC=DN+NC=8,
转移,表达----设CN=x,则EN=DN=_____
求解目标:勾股定理列方程
在Rt△______中,勾股定理列方程为_______________,解得x=_______即CN=_____cm.
【配套小练习】
练习1:如图,有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,点D在BC边上,将直角边AC沿直线AD折叠,点C恰好落在斜边AB上的点E处,则线段CD的长为__________.
练习2:如图,折叠长方形的一边AD,使点D落在BC边上的点F处,若AB=4cm,BC=5cm,则EF的长为________.
【第二次训练】
操作要领:
①折叠属于全等变换,找折痕,利用对应边相等,对应角相等转移条件,表达线段长,利用勾股定理建方程;
②上述思路进行不下去时,从“对称轴上的点到对应点的连线距离相等”,从折痕与背景图形的交点处入手,结合所求目标,连接对应线段,表达求解;或者考虑“折痕”为对称轴,“对应点所连线段被对称轴垂直平分”,利用垂直平分(题目中会出现全等或相似)解题.(这两条性质可以逐一尝试)
【例题2】如图,将长为4cm,宽为2cm的长方形纸片ABCD折叠,使点B落在CD边的中点E处,压平后得到折痕MN,则线段AM的长为__________.
分析思路:
读题标注、转化;
长方形,折叠,中点,目标,如右图所示
背景图形;
长为4,宽为2的长方形,DE=EC=1,E是定点;
分析条件,组合特征;
折叠是全等变换----对应边相等,对应角相等;
上方:AM=MF,但MF所在的直角三角形无相关线段长信息,求解不出来;
下方:BN=EN;______+NC=BN+NC=4,在Rt△______中,勾股定理能够求BN(NE,NC等),但跟目标无关,先不进行计算;
求解目标;
方式一:考虑折叠性质“对称轴上的点到对应点的连线距离相等”,连接MB和ME,则MB=ME,可以用来表达列方程求解;如图所示
转移表达----设AM=x,则DM=_____;在Rt△______中,_____________(用含x的代数式表示);在Rt△______中,_____________(用含x的代数式表示);建立方程为_______________,解得x=_______,即AM=_____.
方式二:考虑折叠性质“对应点所连线段被对称轴垂直平分”,连接BE,则_____被_____垂直平分;如图所示
过点M作MG⊥BC于点G,则△MGN∽△______,且相似比为1:2,由CE的长,可求GN的长,结合AM=BG=BN-GN,(BN可通过第3条中的分析求出)即可求出AM的长.
中间用到一个很重要的结论:“十字结构”会出现全等或相似.而折叠中的垂直平分经常会提供十字结构,以下是一般的“十字结构”的图形和结论.
△ABE≌△BCF
△DCE≌△ABF
△ABE∽△BCF
【配套小练习】-----练习3和练习4均要求用折叠的两种性质解题(每种图中展示一种方法)
练习3:如图,四边形ABCD是边长为9的正方形纸片,将该纸片折叠,使点B落在CD边上的点处,点A的对应点为,折痕为MN.若,则AM的长为__________.
练习4:如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则MN的长为 ,BN的长为 .
练习5:如图,在长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点D与点B重合,折痕为EF,则EF的长为_________.(要求用“对应点的连线被对称轴垂直平分”解题,有其余方法可自行尝试)
练习6:如图,长方形纸片ABCD,AB=5,BC=10,CD上有一点E,ED=2,AD上有一点P,PD=3,过P作PF⊥AD交BC于F,将纸片折叠,使P点与E点重合,折痕与PF交于Q点,与AD交于点G,则PQ的长是(
)(要求用“对应点的连线被对称轴垂直平分”解题,有其余方法可自行尝试)
A.
B.3
C.
D.
练习7:如图,将边长为12cm的正方形ABCD折叠,使得A点落在边CD上的E点,然后压平得折痕FG,若GF的长为13cm,则线段CE的长为_____________.
【第三次训练】
操作要领:
当上述两种思路都进行不下去的时候考虑背景提供的条件,如长方形中折叠会出现等腰三角形(以折痕为底);(原理是:平行+角平分线出现等腰三角形)
【例题3】用长方形下的折叠会出现等腰三角形,快速求BF的长
如图,在长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点D与点B重合,折痕为EF,则BF的长为_________.
拓展:请在右上图中补全(例题2)长方形下的折叠出现的等腰三角形,在图上进行体现,并用此思路尝试求AM的长;
如图,将长为4cm,宽为2cm的长方形纸片ABCD折叠,使点B落在CD边的中点E处,压平后得到折痕MN,则线段AM的长为__________.
【配套小练习】
练习8:如图,长方形ABCD中,AB=15cm,点E在AD上,且AE=9cm,连接EC,将长方形ABCD沿直线BE翻折,点A恰好落在EC上的点A'处,则A'C=_______cm.
练习9:已知一个长方形纸片OABC,OA=6,点P为AB边上一点,AP=2,将△OAP沿OP折叠,点A落在点A′处,延长PA′交边OC与点D,经过点P再次折叠纸片,使点B落在边OC上的点D处,则AB的长为____________.
练习10:如图,四边形ABCD是边长为9的正方形纸片,将该纸片折叠,使点B落在CD边上的点处,点A的对应点为,折痕为MN.若,则AM的长为__________.(请用长方形下的折叠会出现等腰三角形,解题)
【第四次训练】折叠作图训练及计算求解
题目中给出已知的对应点,直接作垂直平分线,找折痕;
题目中没有直接给出的对应点,而是给出对应点满足的条件;
此时往往“折痕过定点”,题目往往会产生圆(圆弧),通过作圆弧找到对应点的位置,再作垂直平分线找折痕.
练习11:如图,在矩形ABCD中,已知AB=12,AD=8,如果将矩形沿直线l翻折后,点A落在边CD的中点E处,直线l分别与边AB,AD交于点M,N,那么MN的长为_________.
练习12:在矩形ABCD中,AB=4,BC=3,点P在线段AB上.若将△DAP沿DP折叠,使点A落在对角线AC上的A′处,则AP的长为_____________.
练习13:如图,矩形ABCD中,AB=2,AD=6,AF=BE=2,点G是线段AD上的动点,将矩形ABCD沿直线EG折叠.当点C的对应点C′落在四边形ABEF对角线所在直线上时,求AC′的长为_____________.
练习14:如图,矩形纸片ABCD中,AB=8cm,BC=20cm,O是BC的中点,沿过O的直线翻折.若点B恰好落在AD上,那么折痕的长度为________.
练习15:在矩形ABCD中,BC=6,CD=8,点P在线段AB上(不含端点A,B)任意一点.若将△PBC沿PC折叠,使点B的对应点B′落在矩形ABCD对角线上时,BP的长为_____________.
用你学到的内容,尝试用多种方法解题。
如图,矩形ABCD中,AB=12,BC=10,点E是BC上一点且BE=2,点F是CD上一点且CF=4,将矩形ABCD折叠,使点E和点F重合,折痕分别与AD、BC交于点HG,则AH的长为__________.
如图,在矩形ABCD中,AB=10,AD=6,沿过点A的直线折叠矩形ABCD,使得点B落在线段CD上,折痕交CB于点F,则AF=________.
8
同课章节目录
