第11章 图形的运动 单元测试-沪教版(上海)七年级上册数学同步练习(Word版 含答案)
文档属性
| 名称 | 第11章 图形的运动 单元测试-沪教版(上海)七年级上册数学同步练习(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 320.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 11:33:38 | ||
图片预览



文档简介
第十一章
图形的运动
单元测试
一、单选题
1.下面的图形中,是中心对称图形的是(
).
A.
B.
C.
D.
2.经过轴对称变换后所得的图形,与原图形相比(
)
A.形状没有改变,大小没有改变
B.形状没有改变,大小有改变
C.形状有改变,大小没有改变
D.形状有改变,大小有改变
3.如图,将△AOB绕点O按顺时针方向旋转45°后得到△COD,若∠AOB=27°,则∠BOC的度数是( )
A.18°
B.27°
C.45°
D.72°
4.如图所示的两个三角形是经过何种变换得到的( )
A.旋转
B.旋转和平移
C.轴对称
D.平移和轴对称
5.将正六边形绕其对称中心旋转后,恰好能与原来的正六边形重合,那么旋转的角度至少是?( )
A.120°
B.60°
C.45°
D.30°
6.由图所示的地板砖各两块所铺成的下列图案中,既是轴对称图形,又是中心对称图形的是(
)
A.
B.
C.
D.
7.如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
A.
B.
C.
D.
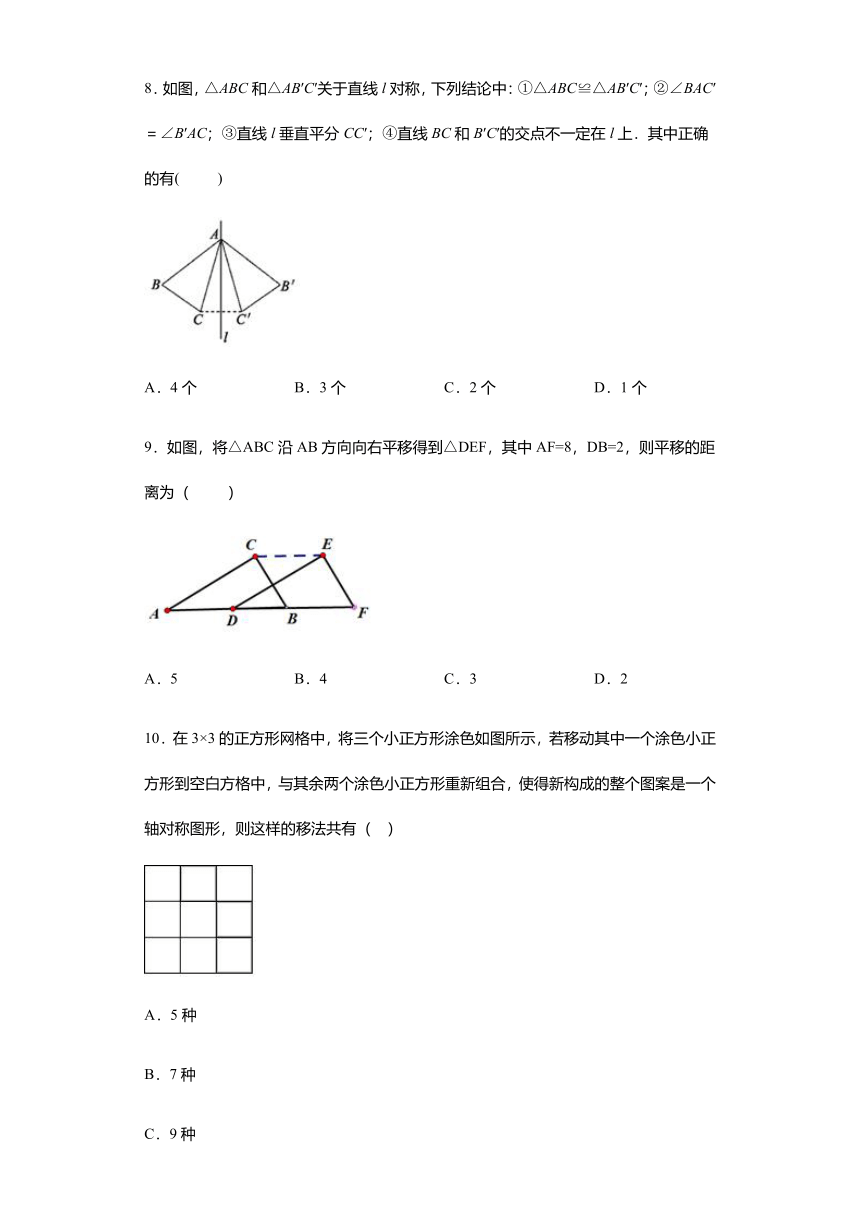
8.如图,△ABC和△AB′C′关于直线l对称,下列结论中:①△ABC≌△AB′C′;②∠BAC′=∠B′AC;③直线l垂直平分CC′;④直线BC和B′C′的交点不一定在l上.其中正确的有(
)
A.4个
B.3个
C.2个
D.1个
9.如图,将△ABC沿AB方向向右平移得到△DEF,其中AF=8,DB=2,则平移的距离为(
)
A.5
B.4
C.3
D.2
10.在3×3的正方形网格中,将三个小正方形涂色如图所示,若移动其中一个涂色小正方形到空白方格中,与其余两个涂色小正方形重新组合,使得新构成的整个图案是一个轴对称图形,则这样的移法共有(??
)
A.5种
B.7种
C.9种
D.10种
二、填空题
11.黑板上写着在正对着黑板的镜子里的像是__________.
12.平移改变的是图形的______
.
13.如图的雪花有______条对称轴
14.一个正三角形至少绕其中心旋转_________度,就能与其自身重合.
15.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形
荷塘上架设小桥.若荷塘周长为280m,且桥宽忽略不计,则小桥总长为
m.
16.如图,一块含有角()的直角三角板,在水平的桌面上绕点按顺时针方向旋转到的位置,点、、在一直线上,那么旋转角是______.
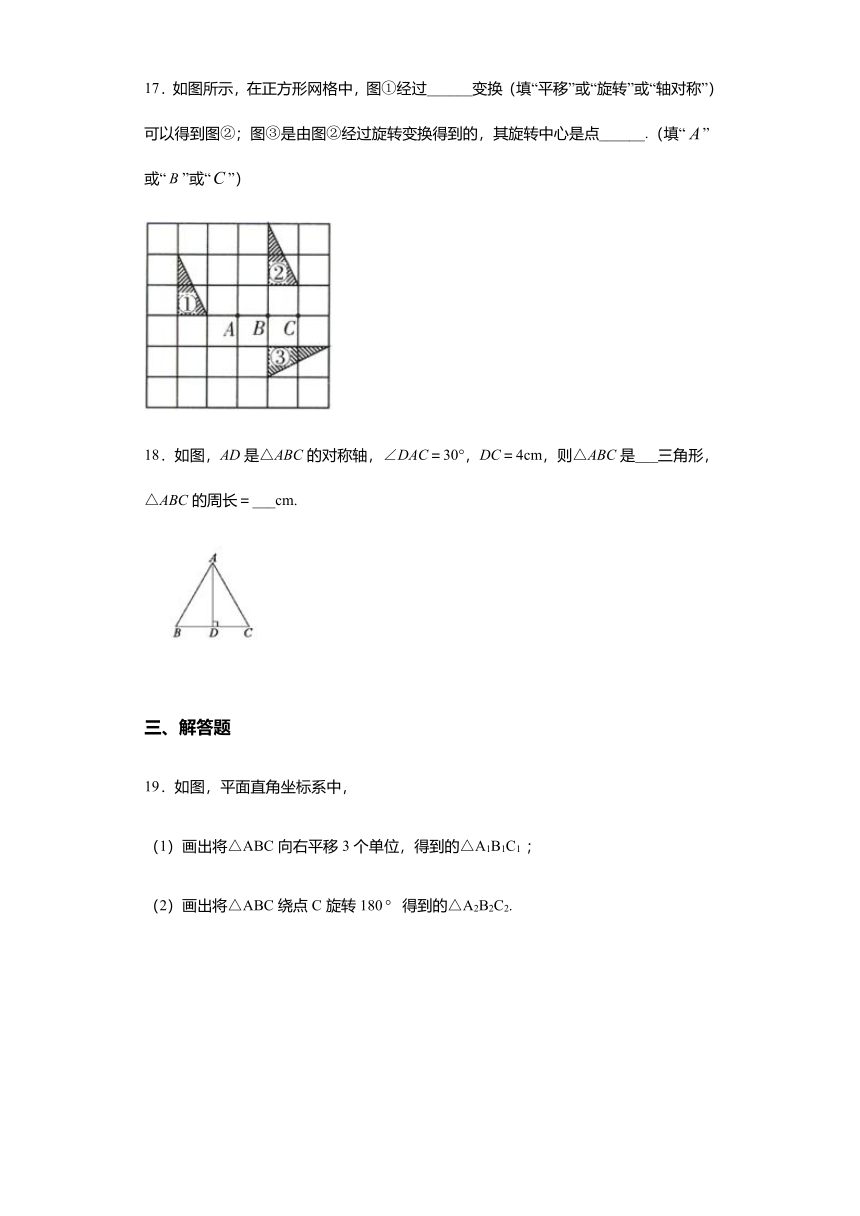
17.如图所示,在正方形网格中,图①经过______变换(填“平移”或“旋转”或“轴对称”)可以得到图②;图③是由图②经过旋转变换得到的,其旋转中心是点______.(填“”或“”或“”)
18.如图,AD是△ABC的对称轴,∠DAC=30°,DC=4cm,则△ABC是___三角形,△ABC的周长=___cm.
三、解答题
19.如图,平面直角坐标系中,
(1)画出将△ABC向右平移3个单位,得到的△A1B1C1
;
(2)画出将△ABC绕点C旋转180
得到的△A2B2C2.
20.如图所示的图形是不是轴对称图形?如果是轴对称图形,它有几条对称轴?
21.如图所示,在图形中标出点A、B、C关于直线l的对称点D、E、F.若M为AB的中点,在图中标出它的对称点N.若AB=10,AB边上的高为4,则△DEF的面积为多少?
22.如图,在4个大小相同的正方形组成的图形中,请你再添加一个正方形,使整个图形是轴对称图形(最少画三个).
23.如图,和都是等边三角形.
(1)沿着______所在的直线翻折能与重合;
(2)如果旋转后能与重合,则在图形所在的平面上可以作为旋转中心的点是______;
(3)请说出2中一种旋转的旋转角的度数______.
24.如图所示,张三打算在院落种上蔬菜.已知院落为东西长为32米,南北宽为20米的长方形,为了行走方便,要修筑同样宽度的三条小路,东西两条,南北一条,余下的部分种上各类蔬菜.若每条小路的宽均为1米.
(1)求蔬菜的种植面积;
(2)若每平方米的每季蔬菜的值为3元,成本为1元,这个院落每季的产值是多少?
参考答案
1.A
2.A
3.A
4.D
5.B
6.A
7.A
8.B
9.C
10.C
11.
12.位置
13.3
14.120°
15.140m.
16.
17.平移
18.等边,
24
19.解:
(1)由图可得:A(-3,3),B(-5,1),C(-2,0),将△ABC向右平移3个单位,点A、B、C的对应点A1(0,3)、B1(-2,1)、C1(1,0),如图所示:
(2)△ABC绕点C旋转180
得到的△A2B2C2的坐标A2(-1,3),B2(1,-1),C2(-2,0),如图所示:
20.是轴对称图形,有4条对称轴
21.如图所示,
∵AB=10,∴DE=AB=10,
∴.
答:△DEF的面积是20.
22.如图所示,
23.
(1)∵和都是等边三角形,
∴和是全等三角形,
∴△ABC沿着AC所在的直线翻折能与△ADC重合.
故填AC;
(2)将△ABC旋转后与重合,则可以以点A为旋转中心逆时针旋转60或以点C为旋转中心顺时针旋转60,或以AC的中点为旋转中心旋转180即可;
(3)以点A
、点C为旋转中心时都旋转,以AC中点旋转时旋转180.
24.解:(1)由题意可得:
蔬菜的种植面积为:(32-1)×(20-2)=558(平方米);
(2)根据题意可得:
这个院落每季的产值是:558×(3-1)=1116(元),
答:这个院落每季的产值是1116元.
图形的运动
单元测试
一、单选题
1.下面的图形中,是中心对称图形的是(
).
A.
B.
C.
D.
2.经过轴对称变换后所得的图形,与原图形相比(
)
A.形状没有改变,大小没有改变
B.形状没有改变,大小有改变
C.形状有改变,大小没有改变
D.形状有改变,大小有改变
3.如图,将△AOB绕点O按顺时针方向旋转45°后得到△COD,若∠AOB=27°,则∠BOC的度数是( )
A.18°
B.27°
C.45°
D.72°
4.如图所示的两个三角形是经过何种变换得到的( )
A.旋转
B.旋转和平移
C.轴对称
D.平移和轴对称
5.将正六边形绕其对称中心旋转后,恰好能与原来的正六边形重合,那么旋转的角度至少是?( )
A.120°
B.60°
C.45°
D.30°
6.由图所示的地板砖各两块所铺成的下列图案中,既是轴对称图形,又是中心对称图形的是(
)
A.
B.
C.
D.
7.如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
A.
B.
C.
D.
8.如图,△ABC和△AB′C′关于直线l对称,下列结论中:①△ABC≌△AB′C′;②∠BAC′=∠B′AC;③直线l垂直平分CC′;④直线BC和B′C′的交点不一定在l上.其中正确的有(
)
A.4个
B.3个
C.2个
D.1个
9.如图,将△ABC沿AB方向向右平移得到△DEF,其中AF=8,DB=2,则平移的距离为(
)
A.5
B.4
C.3
D.2
10.在3×3的正方形网格中,将三个小正方形涂色如图所示,若移动其中一个涂色小正方形到空白方格中,与其余两个涂色小正方形重新组合,使得新构成的整个图案是一个轴对称图形,则这样的移法共有(??
)
A.5种
B.7种
C.9种
D.10种
二、填空题
11.黑板上写着在正对着黑板的镜子里的像是__________.
12.平移改变的是图形的______
.
13.如图的雪花有______条对称轴
14.一个正三角形至少绕其中心旋转_________度,就能与其自身重合.
15.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形
荷塘上架设小桥.若荷塘周长为280m,且桥宽忽略不计,则小桥总长为
m.
16.如图,一块含有角()的直角三角板,在水平的桌面上绕点按顺时针方向旋转到的位置,点、、在一直线上,那么旋转角是______.
17.如图所示,在正方形网格中,图①经过______变换(填“平移”或“旋转”或“轴对称”)可以得到图②;图③是由图②经过旋转变换得到的,其旋转中心是点______.(填“”或“”或“”)
18.如图,AD是△ABC的对称轴,∠DAC=30°,DC=4cm,则△ABC是___三角形,△ABC的周长=___cm.
三、解答题
19.如图,平面直角坐标系中,
(1)画出将△ABC向右平移3个单位,得到的△A1B1C1
;
(2)画出将△ABC绕点C旋转180
得到的△A2B2C2.
20.如图所示的图形是不是轴对称图形?如果是轴对称图形,它有几条对称轴?
21.如图所示,在图形中标出点A、B、C关于直线l的对称点D、E、F.若M为AB的中点,在图中标出它的对称点N.若AB=10,AB边上的高为4,则△DEF的面积为多少?
22.如图,在4个大小相同的正方形组成的图形中,请你再添加一个正方形,使整个图形是轴对称图形(最少画三个).
23.如图,和都是等边三角形.
(1)沿着______所在的直线翻折能与重合;
(2)如果旋转后能与重合,则在图形所在的平面上可以作为旋转中心的点是______;
(3)请说出2中一种旋转的旋转角的度数______.
24.如图所示,张三打算在院落种上蔬菜.已知院落为东西长为32米,南北宽为20米的长方形,为了行走方便,要修筑同样宽度的三条小路,东西两条,南北一条,余下的部分种上各类蔬菜.若每条小路的宽均为1米.
(1)求蔬菜的种植面积;
(2)若每平方米的每季蔬菜的值为3元,成本为1元,这个院落每季的产值是多少?
参考答案
1.A
2.A
3.A
4.D
5.B
6.A
7.A
8.B
9.C
10.C
11.
12.位置
13.3
14.120°
15.140m.
16.
17.平移
18.等边,
24
19.解:
(1)由图可得:A(-3,3),B(-5,1),C(-2,0),将△ABC向右平移3个单位,点A、B、C的对应点A1(0,3)、B1(-2,1)、C1(1,0),如图所示:
(2)△ABC绕点C旋转180
得到的△A2B2C2的坐标A2(-1,3),B2(1,-1),C2(-2,0),如图所示:
20.是轴对称图形,有4条对称轴
21.如图所示,
∵AB=10,∴DE=AB=10,
∴.
答:△DEF的面积是20.
22.如图所示,
23.
(1)∵和都是等边三角形,
∴和是全等三角形,
∴△ABC沿着AC所在的直线翻折能与△ADC重合.
故填AC;
(2)将△ABC旋转后与重合,则可以以点A为旋转中心逆时针旋转60或以点C为旋转中心顺时针旋转60,或以AC的中点为旋转中心旋转180即可;
(3)以点A
、点C为旋转中心时都旋转,以AC中点旋转时旋转180.
24.解:(1)由题意可得:
蔬菜的种植面积为:(32-1)×(20-2)=558(平方米);
(2)根据题意可得:
这个院落每季的产值是:558×(3-1)=1116(元),
答:这个院落每季的产值是1116元.
