人教七年级上 4.3.3余角和补角
文档属性
| 名称 | 人教七年级上 4.3.3余角和补角 |  | |
| 格式 | rar | ||
| 文件大小 | 208.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-09-15 22:08:06 | ||
图片预览


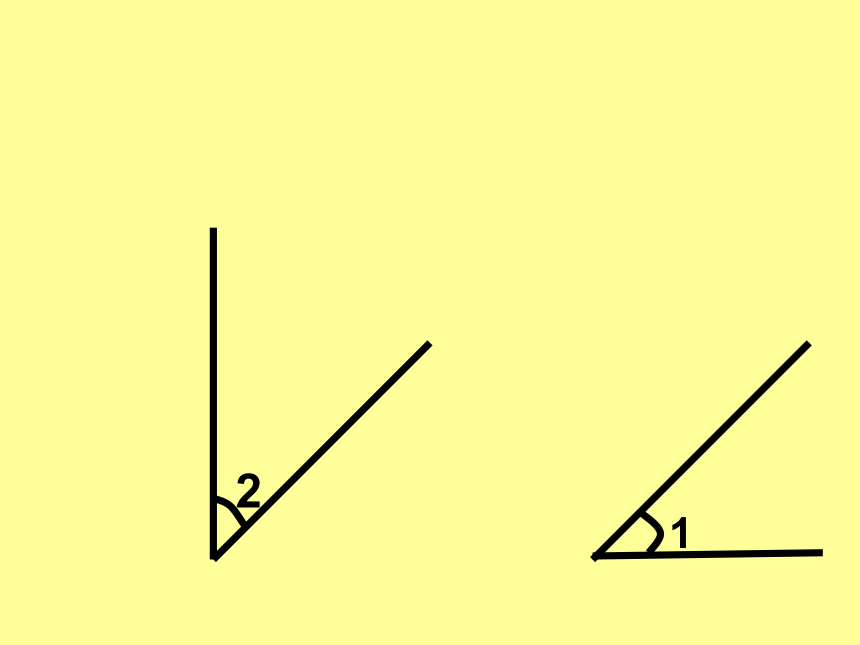



文档简介
(共36张PPT)
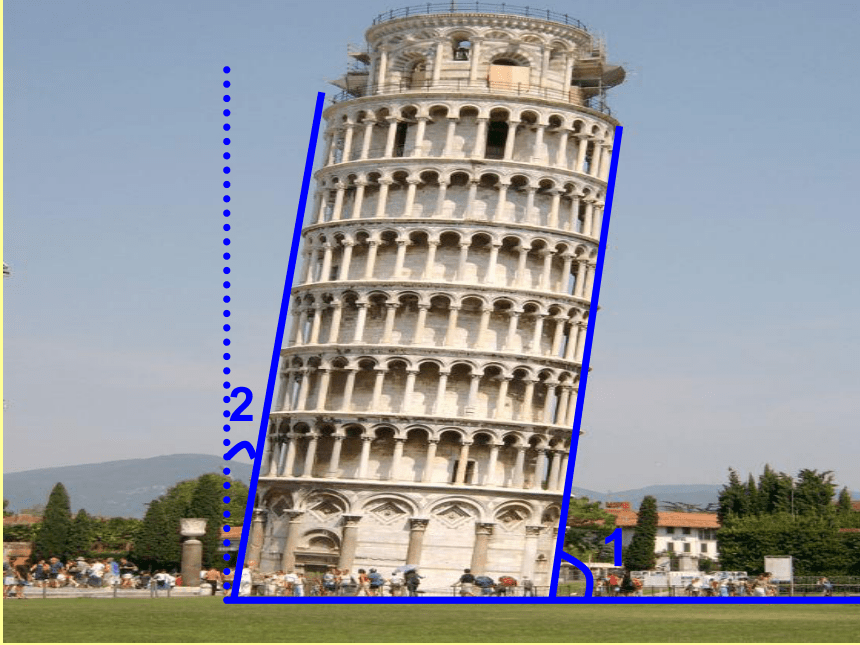
1
2
2
1
1
2
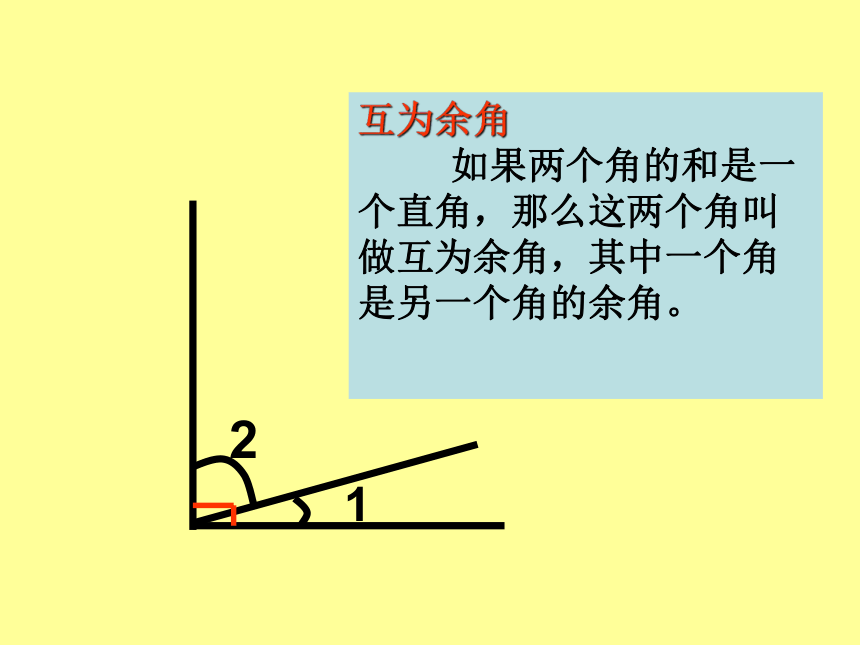
互为余角
如果两个角的和是一个直角,那么这两个角叫做互为余角,其中一个角是另一个角的余角。
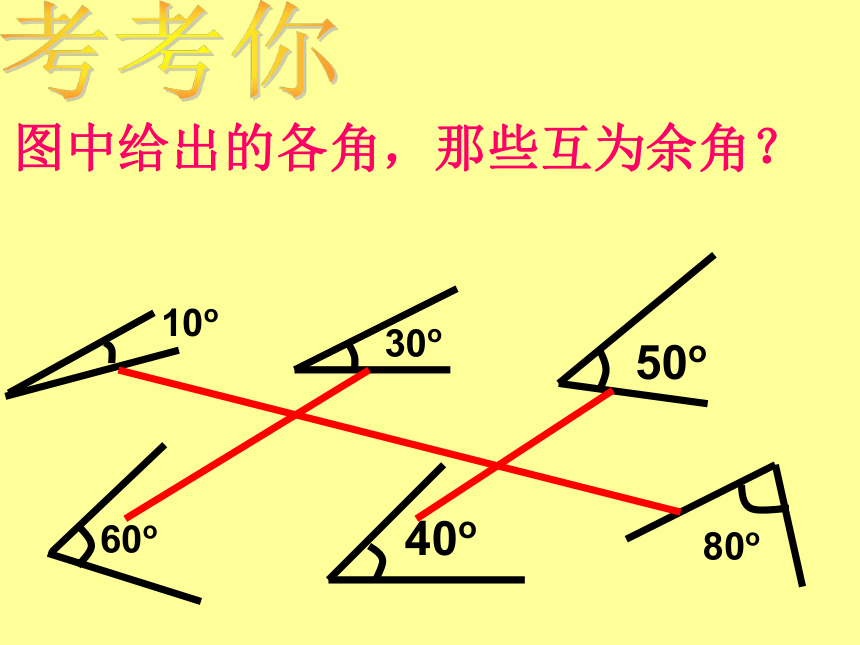
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
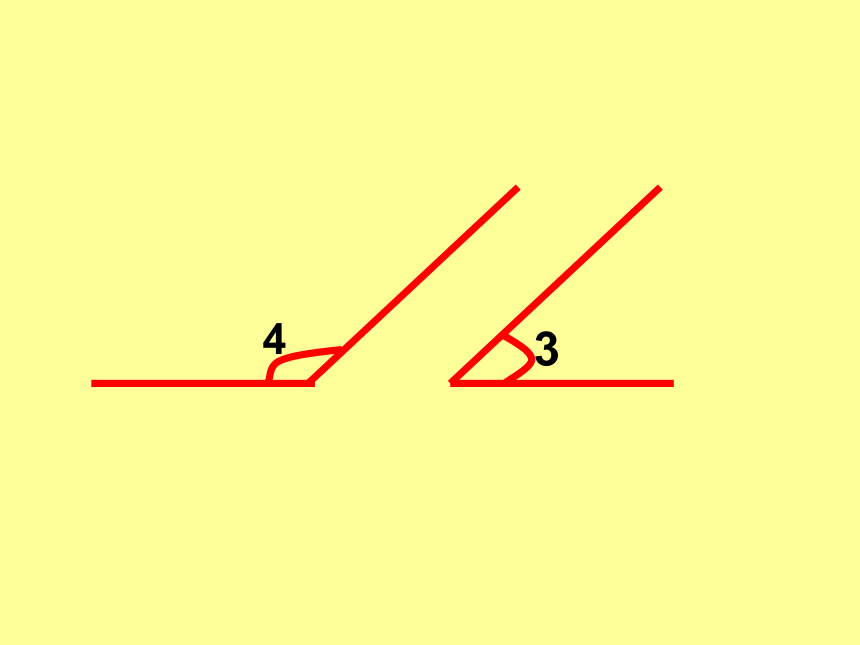
3
4
3
4
3
4
互为补角
如果两个角的和是一个平角,那么这两个角叫做互为补角,其中一个角是另一个角的补角。
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
我来试一试:
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
x
90° x
180° x
练习
一、填空
1、70°的余角是 ,补角是 。
2、 ∠ ( ∠ <90 ° )的余角是 ,它的补角是 。
110 °
20°
90°- ∠
180°- ∠
重要提醒:(如何表示一个角的余角和补角)
锐角∠ 的余角是(90 °—∠ )
∠ 的补角是(180 °—∠ )
例1 若一个角的补角等于它的余角的
4 倍,求这个角的度数。
解: 设这个角是x °,则它的补角是 ( 180°-x°),余角是(90°-x°) 。
根据题意得:
(180°-x°)= 4 (90°-x°)
解得: x =60
答:这个角的度数是60 °。
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
2
1
4
3
探究:余角和补角的性质
补角性质:
同角或等角的补角相等
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
探究:余角和补角的性质
余角性质:
同角或等角的余角相等
如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?
答: ∠1 = ∠2
因为∠1+ ∠BOD = 90 °
∠2+ ∠BOD = 90 °
所以∠1 = ∠2
A
O
B
C
D
(同角的余角相等)
1
2
1
2
2
1
∠1+∠2=90°
∠1+∠2=180°
等角的余角相等
等角的补角相等.
互 余 互 补
数量
关系
对
应
图
形
性
质
如图,已知AB是一直线,O是直线AB上的一点。OC是∠ AOB的平分线, ∠ DOE是直角,图中哪些角互余?哪些角互补?哪些角相等?
A
O
B
E
C
D
1
2
3
4
探索研究
A
B
C
D
E
F
G
如图,E、F是直线DG上两点
∠BEF = ∠BFE
∠AED = ∠CFG = 90 °
找出图中相等的角并说明理由。
东
南
西
北
东南
西南
西北
东北
你知道方位角吗?
例1 如图,OA是表示北偏东300方向的一条射线,仿照
这条射线,画出表示下列方向的角:
(1)南偏东250 (2)北偏西600
A
东
南
西
北
300
25°
60°
例2 如图,货轮O在航行过程中,发现灯塔A在南偏东60°的方向上。同时,在它北偏东40°、南偏西10°、西北方向上又分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D的射线。
60°
O
A
东
南
西
北
B
40°
60°
O
A
东
南
西
北
D
C
2、如图,OA表示北偏东32°方向线, OB表示南偏东43°方向线,则∠AOB等于————。
3、A看B的方向是北偏东30°,那么B看A的方向是( )
(A)南偏东60°(B)南偏西60°
(C)南偏东30° (D)南偏西30°
A
东
北
东
北
1
2
B
4、 小明从点A出发向北偏西50°方向走了3米,到达点B,小林从点A出发向南偏西40°方向走了4米,试画图确定出A、B、C三点的位置(用1厘米表示3米),并从图上求出B点到C点的实际距离。
东
南
西
北
A
500
400
B
C
互为余角
如果 的和是一个 ,那么这两个角叫做 余角,其中一个角是 的余角。
互为补角
如果 的和是一个 ,那么这两个角叫做 补角,其中一个角是 的补角。
两个角
直角
互为
另一个角
两个角
互为
另一个角
平角
若∠1 + ∠2 =180 °,
则 .( )
若∠1和∠2互补,
则 .( )
若∠3 + ∠4 =90 °,则 .( )
若∠3和∠4互余,
则 .( )
3
4
1
2
∠1和∠2互补
互补定义
∠1 + ∠2 =180 °
互补定义
∠3和∠4互余
互余定义
∠3 + ∠4 =90 °
互余定义
∠1和∠2互余,∠3和∠4互余,如果∠1=∠3,那么, ∠2和∠4相等吗?为什么?
1
2
3
4
3
3
3
补角性质:
同角或等角的补角相等。
余角性质:
同角或等角的余角相等。
如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?
答: ∠1 = ∠2
因为∠1+ ∠BOD = 90 °
∠2+ ∠BOD = 90 °
所以∠1 = ∠2
A
O
B
C
D
(同角的余角相等)
1
2
互为余角 互为补角
对应图形
数量关系
性 质
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等。
同角或等角的补角相等。
1
2
1
2
A
O
B
E
D
C
∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
2.O为直线AB上的一点,OD平分∠AOB,
∠COE = 90 °
则∠BOC = ,
∠COD = 。
检测
∠DOE
∠AOE
30 °
同角或等角的补角相等
同角或等角的余角相等.
如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?
1
2
2
1
1
2
互为余角
如果两个角的和是一个直角,那么这两个角叫做互为余角,其中一个角是另一个角的余角。
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
3
4
3
4
3
4
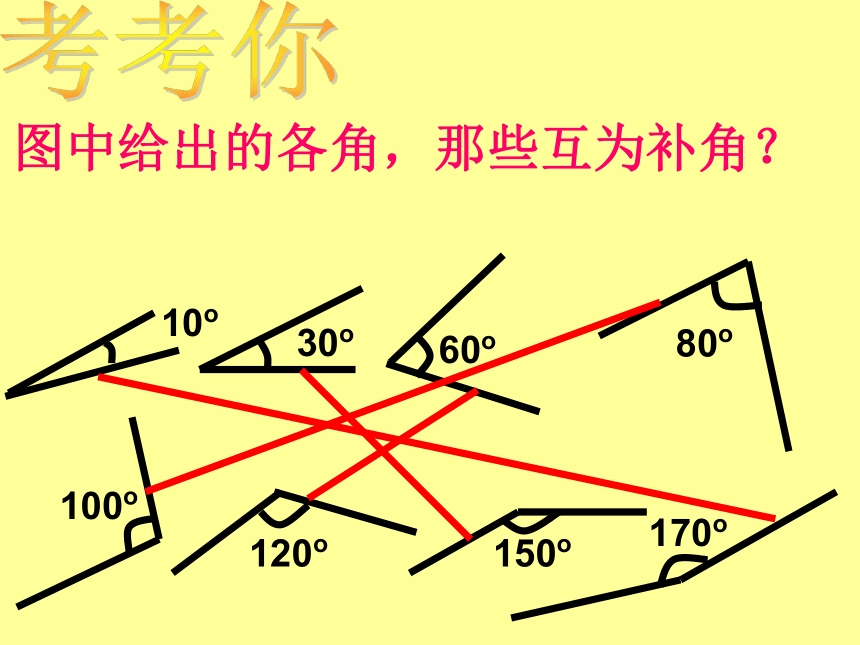
互为补角
如果两个角的和是一个平角,那么这两个角叫做互为补角,其中一个角是另一个角的补角。
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
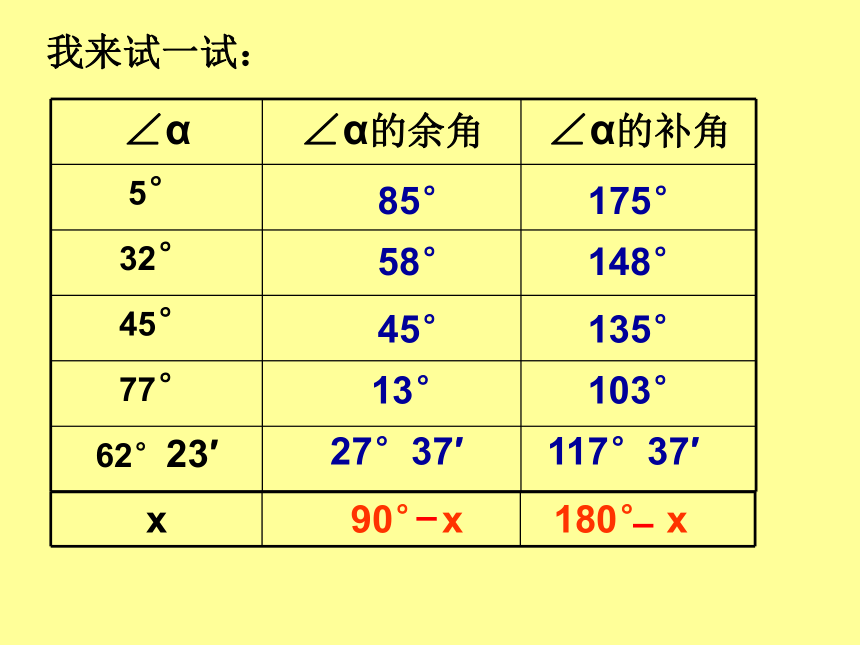
我来试一试:
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
x
90° x
180° x
练习
一、填空
1、70°的余角是 ,补角是 。
2、 ∠ ( ∠ <90 ° )的余角是 ,它的补角是 。
110 °
20°
90°- ∠
180°- ∠
重要提醒:(如何表示一个角的余角和补角)
锐角∠ 的余角是(90 °—∠ )
∠ 的补角是(180 °—∠ )
例1 若一个角的补角等于它的余角的
4 倍,求这个角的度数。
解: 设这个角是x °,则它的补角是 ( 180°-x°),余角是(90°-x°) 。
根据题意得:
(180°-x°)= 4 (90°-x°)
解得: x =60
答:这个角的度数是60 °。
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
2
1
4
3
探究:余角和补角的性质
补角性质:
同角或等角的补角相等
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
探究:余角和补角的性质
余角性质:
同角或等角的余角相等
如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?
答: ∠1 = ∠2
因为∠1+ ∠BOD = 90 °
∠2+ ∠BOD = 90 °
所以∠1 = ∠2
A
O
B
C
D
(同角的余角相等)
1
2
1
2
2
1
∠1+∠2=90°
∠1+∠2=180°
等角的余角相等
等角的补角相等.
互 余 互 补
数量
关系
对
应
图
形
性
质
如图,已知AB是一直线,O是直线AB上的一点。OC是∠ AOB的平分线, ∠ DOE是直角,图中哪些角互余?哪些角互补?哪些角相等?
A
O
B
E
C
D
1
2
3
4
探索研究
A
B
C
D
E
F
G
如图,E、F是直线DG上两点
∠BEF = ∠BFE
∠AED = ∠CFG = 90 °
找出图中相等的角并说明理由。
东
南
西
北
东南
西南
西北
东北
你知道方位角吗?
例1 如图,OA是表示北偏东300方向的一条射线,仿照
这条射线,画出表示下列方向的角:
(1)南偏东250 (2)北偏西600
A
东
南
西
北
300
25°
60°
例2 如图,货轮O在航行过程中,发现灯塔A在南偏东60°的方向上。同时,在它北偏东40°、南偏西10°、西北方向上又分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D的射线。
60°
O
A
东
南
西
北
B
40°
60°
O
A
东
南
西
北
D
C
2、如图,OA表示北偏东32°方向线, OB表示南偏东43°方向线,则∠AOB等于————。
3、A看B的方向是北偏东30°,那么B看A的方向是( )
(A)南偏东60°(B)南偏西60°
(C)南偏东30° (D)南偏西30°
A
东
北
东
北
1
2
B
4、 小明从点A出发向北偏西50°方向走了3米,到达点B,小林从点A出发向南偏西40°方向走了4米,试画图确定出A、B、C三点的位置(用1厘米表示3米),并从图上求出B点到C点的实际距离。
东
南
西
北
A
500
400
B
C
互为余角
如果 的和是一个 ,那么这两个角叫做 余角,其中一个角是 的余角。
互为补角
如果 的和是一个 ,那么这两个角叫做 补角,其中一个角是 的补角。
两个角
直角
互为
另一个角
两个角
互为
另一个角
平角
若∠1 + ∠2 =180 °,
则 .( )
若∠1和∠2互补,
则 .( )
若∠3 + ∠4 =90 °,则 .( )
若∠3和∠4互余,
则 .( )
3
4
1
2
∠1和∠2互补
互补定义
∠1 + ∠2 =180 °
互补定义
∠3和∠4互余
互余定义
∠3 + ∠4 =90 °
互余定义
∠1和∠2互余,∠3和∠4互余,如果∠1=∠3,那么, ∠2和∠4相等吗?为什么?
1
2
3
4
3
3
3
补角性质:
同角或等角的补角相等。
余角性质:
同角或等角的余角相等。
如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?
答: ∠1 = ∠2
因为∠1+ ∠BOD = 90 °
∠2+ ∠BOD = 90 °
所以∠1 = ∠2
A
O
B
C
D
(同角的余角相等)
1
2
互为余角 互为补角
对应图形
数量关系
性 质
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等。
同角或等角的补角相等。
1
2
1
2
A
O
B
E
D
C
∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
2.O为直线AB上的一点,OD平分∠AOB,
∠COE = 90 °
则∠BOC = ,
∠COD = 。
检测
∠DOE
∠AOE
30 °
同角或等角的补角相等
同角或等角的余角相等.
如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?
