3.3.1 二次函数y=ax2的图象和性质(含答案)
文档属性
| 名称 | 3.3.1 二次函数y=ax2的图象和性质(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三章 二次函数
3.3 二次函数的图象于性质
第1课时
知识梳理
知识点1 二次函数y=x2的图象及其性质
作二次函数y=x2图象的步骤:
(1)列表:
x … -3 -2 -1 0 1 2 3 …
y … 9 4 1 0 1 4 9 …
(2)在平面直角坐标系中描点;
(3)连线:用光滑的曲线将这7个点连接起来,便得到y=x2的图象.
2.二次函数y=x2的性质:
二次函数y=x2的图象是一条____________,它的开口_____________,且关于_________对称.
对称轴与抛物线的交点(0,0)是抛物线的_________,它是图象的______________。
当x>0时,y的值随x值的增大而_____________;当x<0时,y的值随x值的增大而__________。
知识点2 二次函数y=-x2的图象及其性质
如图所示,二次函数y=-x2的图象是一条______________,它的开口____________,且关于_________对称。
对称轴与抛物线的交点(0,0)是抛物线的____________,它是图象的_____________。
当x>0时,y的值随x值的增大而___________;当x<0时,y的值随x值的增大而____________。
考点突破
考点1 作二次函数y=ax2的图象
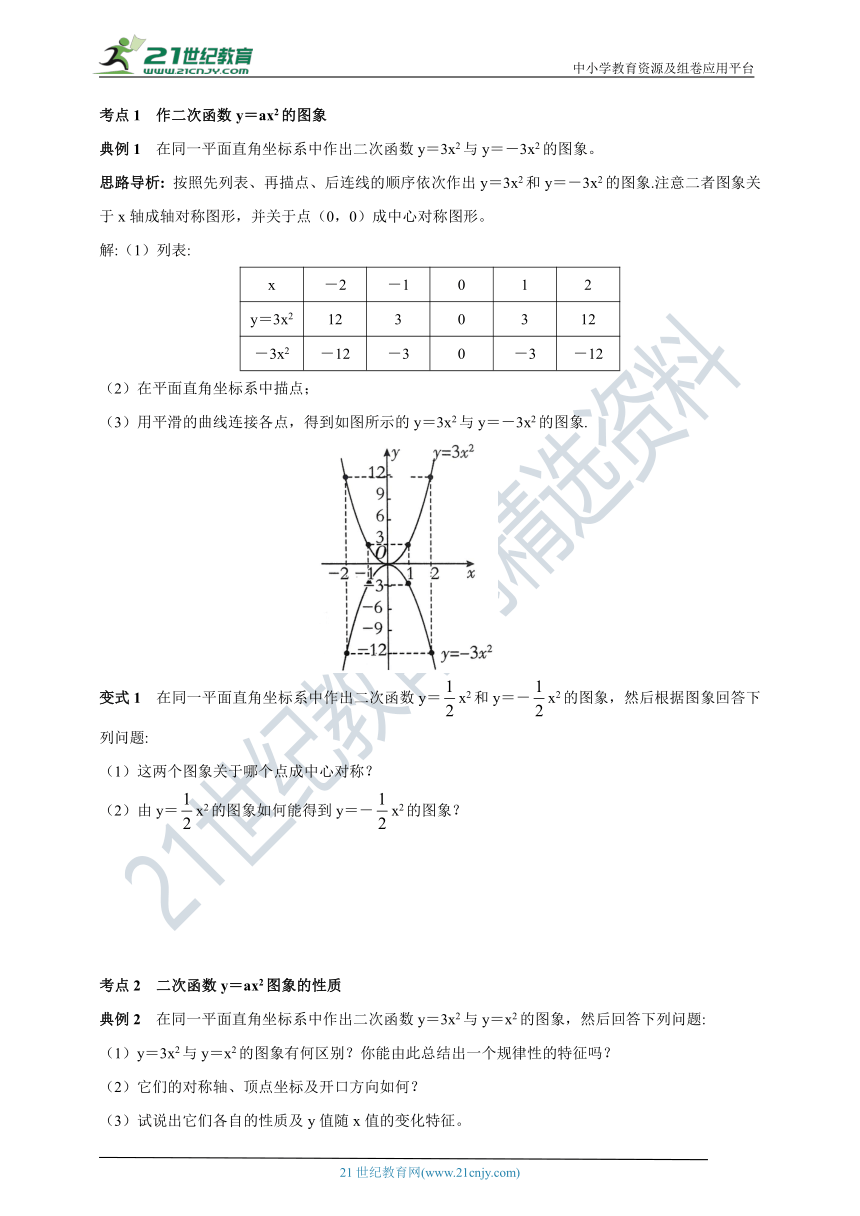
典例1 在同一平面直角坐标系中作出二次函数y=3x2与y=-3x2的图象。
思路导析: 按照先列表、再描点、后连线的顺序依次作出y=3x2和y=-3x2的图象.注意二者图象关于x轴成轴对称图形,并关于点(0,0)成中心对称图形。
解:(1)列表:
x -2 -1 0 1 2
y=3x2 12 3 0 3 12
-3x2 -12 -3 0 -3 -12
(2)在平面直角坐标系中描点;
(3)用平滑的曲线连接各点,得到如图所示的y=3x2与y=-3x2的图象.
变式1 在同一平面直角坐标系中作出二次函数y=x2和y=-x2的图象,然后根据图象回答下列问题:
(1)这两个图象关于哪个点成中心对称?
(2)由y=x2的图象如何能得到y=-x2的图象?
考点2 二次函数y=ax2图象的性质
典例2 在同一平面直角坐标系中作出二次函数y=3x2与y=x2的图象,然后回答下列问题:
(1)y=3x2与y=x2的图象有何区别?你能由此总结出一个规律性的特征吗?
(2)它们的对称轴、顶点坐标及开口方向如何?
(3)试说出它们各自的性质及y值随x值的变化特征。
思路导析: 用列表、描点、连线的方法作出二次函数y=3x2和y=x2的图象,再依据图象回答上述各个问题。
解:列表:
x … -2 -1.5 -1 0 1 1.5 2 …
y=3x2 … 12
3 0 3
12 …
y=x2 … 4
1 0 1
4 …
根据上表描点、连线,作出二次函数y=3x2与y=x2的图象(如图所示).
(1)由图象可以看出,y=3x2与y=x2的图象只有开口的大小不相同,y=x2比y=3x2的开口要大一些.由此我们可以猜想:对于抛物线y=a1x2与y=a2x2,当|a1|>| a2|时,y=a1x2的开口比y=a2x2的开口小一些;
(2)由图象可以看出,y=3x2与y=x2的对称轴均为y轴,顶点坐标均为(0,0),开口方向均向上;
(3)抛物线y=3x2与y=x2都是开口向上,以y轴为对称轴的抛物线,在x<0时,y的值均随x值的增大而减小;在x>0时,y的值均随x值的增大而增大。
友情提示 对于二次函数y=ax2,a的绝对值越大,抛物线的开口反而越小。
变式2 在同一平面直角坐标系中作二次函数y=-x2与y=-x2的图象,然后回答下列问题:
(1)它们的开口方向、对称轴和顶点坐标分别是什么?
(2)请描述一下在对称轴的左侧函数值的变化情况。
巩固提高
1.下列有关抛物线y=x2和y=-x2的关系的说法中,错误的是( )
A.抛物线y=x2与y=-x2有共同的顶点和对称轴
B.抛物线y=x2与y=-x2关于x轴对称
C.抛物线y=x2与y=-x2的形状相同,开口方向相反
D.点A(-2,4)在抛物线y=x2上,也在抛物线y=-x2上
2.已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )
3.如果抛物线y=(m-1)x2的开口向上,那么m的取值范围是________________。
4.抛物线y=-x2的顶点是___________,对称轴是_________,开口向________,顶点是抛物线的最________(填“高”或“低”)点.
5.抛物线y=x2的顶点是___________,对称轴是___________,开口向_________,顶点是抛物线的最
___________(填“高”或“低”)点。
6.若点A(2,m)在抛物线y=x2上,则点A关于y轴对称点的坐标是_____________。
7.作二次函数y=-x2的图象,并解答下列问题:
(1)若A(1,y1),B(2,y2)是抛物线y=-x2上两点,则y1________(填“>”“<”或“=”)y2;
(2)当x_________时,y随x的增大而增大,当x=0时,y取最________值,这个值是_________。
(3)若点C(m,-4)在抛物线y=-x2上,求m的值。
8.画出二次函数y=-x2的图象,并根据图象解答下列问题:
(1)当x=时,y的值是多少?
(2)当y=-2时,x的值是多少?
(3)当x>0时,y随x的增大如何变化?当x<0时,y随x的增大如何变化?
(4)当x取何值时,y有最大值?最大值是多少?
9.已知点A(1,a)在抛物线y=x2上。
(1)求点A的坐标;
(2)在x轴上是否存在点P,使得△OAP是等腰三角形?若存在,求出点P的坐标;若不存在,说明理由。
体验中考
1.(2019·益阳)下列函数中,y总随x的增大而减小的是( )
A. y=4x B. y=-4x C. y=x-4 D.y=x2
2.(2018·广州)已知二次函数y=x2,当x>0时,y随x的增大而_______(填“增大”或“减小”)。
参考答案
知识梳理
知识点1: 2.抛物线 向上 y轴 顶点 最低点 增大 减小
知识点2: 抛物线 向下 y轴 顶点 最高点 减小 增大
考点突破
1,解:图象略
(1)这两个图象关于坐标原点成中心对称;
(2)将二次函数y=x2的图象绕坐标原点旋转180?,或沿x轴翻折,可得到二次函数y=-x2的图象。
2,解:图象略.
(1)它们的开口方向均向下,对称轴均为y轴,顶点坐标均为(0,0);
(2)在对称轴的左侧,它们的函数值均随 值的增大而增大.
巩固提高
1. D 2. C 3. m>1 4. (0,0) y轴 下 高
5. (0,0) у轴 上 低 6. (-2,4)
7图象略. (1)> (2)<0 (3)±2
8,解:图象如图所示:
(1)当 x=时,y=-;
(2)当y=-2时,=±;
(3)当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大;
(4)当x=0时, y有最大值,最大值为0.
9,解:(1)A(1,1);
(2)存在.这样的点P有四个,
即P 1(,0), P2 (-, 0), P3(2, 0),P 4(1,0).
体验中考
1.B
2,增大 解析:∵二次函数y=x2,开口向上,对称轴为y轴,∴当x>0时, y随x的增大而增大.
_21?????????è?????(www.21cnjy.com)_
第三章 二次函数
3.3 二次函数的图象于性质
第1课时
知识梳理
知识点1 二次函数y=x2的图象及其性质
作二次函数y=x2图象的步骤:
(1)列表:
x … -3 -2 -1 0 1 2 3 …
y … 9 4 1 0 1 4 9 …
(2)在平面直角坐标系中描点;
(3)连线:用光滑的曲线将这7个点连接起来,便得到y=x2的图象.
2.二次函数y=x2的性质:
二次函数y=x2的图象是一条____________,它的开口_____________,且关于_________对称.
对称轴与抛物线的交点(0,0)是抛物线的_________,它是图象的______________。
当x>0时,y的值随x值的增大而_____________;当x<0时,y的值随x值的增大而__________。
知识点2 二次函数y=-x2的图象及其性质
如图所示,二次函数y=-x2的图象是一条______________,它的开口____________,且关于_________对称。
对称轴与抛物线的交点(0,0)是抛物线的____________,它是图象的_____________。
当x>0时,y的值随x值的增大而___________;当x<0时,y的值随x值的增大而____________。
考点突破
考点1 作二次函数y=ax2的图象
典例1 在同一平面直角坐标系中作出二次函数y=3x2与y=-3x2的图象。
思路导析: 按照先列表、再描点、后连线的顺序依次作出y=3x2和y=-3x2的图象.注意二者图象关于x轴成轴对称图形,并关于点(0,0)成中心对称图形。
解:(1)列表:
x -2 -1 0 1 2
y=3x2 12 3 0 3 12
-3x2 -12 -3 0 -3 -12
(2)在平面直角坐标系中描点;
(3)用平滑的曲线连接各点,得到如图所示的y=3x2与y=-3x2的图象.
变式1 在同一平面直角坐标系中作出二次函数y=x2和y=-x2的图象,然后根据图象回答下列问题:
(1)这两个图象关于哪个点成中心对称?
(2)由y=x2的图象如何能得到y=-x2的图象?
考点2 二次函数y=ax2图象的性质
典例2 在同一平面直角坐标系中作出二次函数y=3x2与y=x2的图象,然后回答下列问题:
(1)y=3x2与y=x2的图象有何区别?你能由此总结出一个规律性的特征吗?
(2)它们的对称轴、顶点坐标及开口方向如何?
(3)试说出它们各自的性质及y值随x值的变化特征。
思路导析: 用列表、描点、连线的方法作出二次函数y=3x2和y=x2的图象,再依据图象回答上述各个问题。
解:列表:
x … -2 -1.5 -1 0 1 1.5 2 …
y=3x2 … 12
3 0 3
12 …
y=x2 … 4
1 0 1
4 …
根据上表描点、连线,作出二次函数y=3x2与y=x2的图象(如图所示).
(1)由图象可以看出,y=3x2与y=x2的图象只有开口的大小不相同,y=x2比y=3x2的开口要大一些.由此我们可以猜想:对于抛物线y=a1x2与y=a2x2,当|a1|>| a2|时,y=a1x2的开口比y=a2x2的开口小一些;
(2)由图象可以看出,y=3x2与y=x2的对称轴均为y轴,顶点坐标均为(0,0),开口方向均向上;
(3)抛物线y=3x2与y=x2都是开口向上,以y轴为对称轴的抛物线,在x<0时,y的值均随x值的增大而减小;在x>0时,y的值均随x值的增大而增大。
友情提示 对于二次函数y=ax2,a的绝对值越大,抛物线的开口反而越小。
变式2 在同一平面直角坐标系中作二次函数y=-x2与y=-x2的图象,然后回答下列问题:
(1)它们的开口方向、对称轴和顶点坐标分别是什么?
(2)请描述一下在对称轴的左侧函数值的变化情况。
巩固提高
1.下列有关抛物线y=x2和y=-x2的关系的说法中,错误的是( )
A.抛物线y=x2与y=-x2有共同的顶点和对称轴
B.抛物线y=x2与y=-x2关于x轴对称
C.抛物线y=x2与y=-x2的形状相同,开口方向相反
D.点A(-2,4)在抛物线y=x2上,也在抛物线y=-x2上
2.已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )
3.如果抛物线y=(m-1)x2的开口向上,那么m的取值范围是________________。
4.抛物线y=-x2的顶点是___________,对称轴是_________,开口向________,顶点是抛物线的最________(填“高”或“低”)点.
5.抛物线y=x2的顶点是___________,对称轴是___________,开口向_________,顶点是抛物线的最
___________(填“高”或“低”)点。
6.若点A(2,m)在抛物线y=x2上,则点A关于y轴对称点的坐标是_____________。
7.作二次函数y=-x2的图象,并解答下列问题:
(1)若A(1,y1),B(2,y2)是抛物线y=-x2上两点,则y1________(填“>”“<”或“=”)y2;
(2)当x_________时,y随x的增大而增大,当x=0时,y取最________值,这个值是_________。
(3)若点C(m,-4)在抛物线y=-x2上,求m的值。
8.画出二次函数y=-x2的图象,并根据图象解答下列问题:
(1)当x=时,y的值是多少?
(2)当y=-2时,x的值是多少?
(3)当x>0时,y随x的增大如何变化?当x<0时,y随x的增大如何变化?
(4)当x取何值时,y有最大值?最大值是多少?
9.已知点A(1,a)在抛物线y=x2上。
(1)求点A的坐标;
(2)在x轴上是否存在点P,使得△OAP是等腰三角形?若存在,求出点P的坐标;若不存在,说明理由。
体验中考
1.(2019·益阳)下列函数中,y总随x的增大而减小的是( )
A. y=4x B. y=-4x C. y=x-4 D.y=x2
2.(2018·广州)已知二次函数y=x2,当x>0时,y随x的增大而_______(填“增大”或“减小”)。
参考答案
知识梳理
知识点1: 2.抛物线 向上 y轴 顶点 最低点 增大 减小
知识点2: 抛物线 向下 y轴 顶点 最高点 减小 增大
考点突破
1,解:图象略
(1)这两个图象关于坐标原点成中心对称;
(2)将二次函数y=x2的图象绕坐标原点旋转180?,或沿x轴翻折,可得到二次函数y=-x2的图象。
2,解:图象略.
(1)它们的开口方向均向下,对称轴均为y轴,顶点坐标均为(0,0);
(2)在对称轴的左侧,它们的函数值均随 值的增大而增大.
巩固提高
1. D 2. C 3. m>1 4. (0,0) y轴 下 高
5. (0,0) у轴 上 低 6. (-2,4)
7图象略. (1)> (2)<0 (3)±2
8,解:图象如图所示:
(1)当 x=时,y=-;
(2)当y=-2时,=±;
(3)当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大;
(4)当x=0时, y有最大值,最大值为0.
9,解:(1)A(1,1);
(2)存在.这样的点P有四个,
即P 1(,0), P2 (-, 0), P3(2, 0),P 4(1,0).
体验中考
1.B
2,增大 解析:∵二次函数y=x2,开口向上,对称轴为y轴,∴当x>0时, y随x的增大而增大.
_21?????????è?????(www.21cnjy.com)_
