7.3 平行线的判定 课件(29张PPT)
文档属性
| 名称 | 7.3 平行线的判定 课件(29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 14:49:34 | ||
图片预览





文档简介
7.3 平行线的判定
1
2
l2
l1
A
B
装修师傅随身只带了一个量角器,要判断一块破碎的玻璃板的上下两边是否平行,你能帮助他解决这个问题吗?
?
导入新知
2. 能根据“同位角相等,两直线平行”证明“内错角相等,两直线平行”,“同旁内角互补,两直线平行” 并能简单地应用这些结论
1. 初步了解证明的基本步骤和书写格式.
素养目标
3. 能够根据平行线的判定方法进行简单的推理.
●
一、放
二、靠
三、推
四、画
我们已经学习过用三角尺和直尺画平行线的方法.
探究新知
知识点 1
同位角相等两直线平行
b
A
2
1
a
B
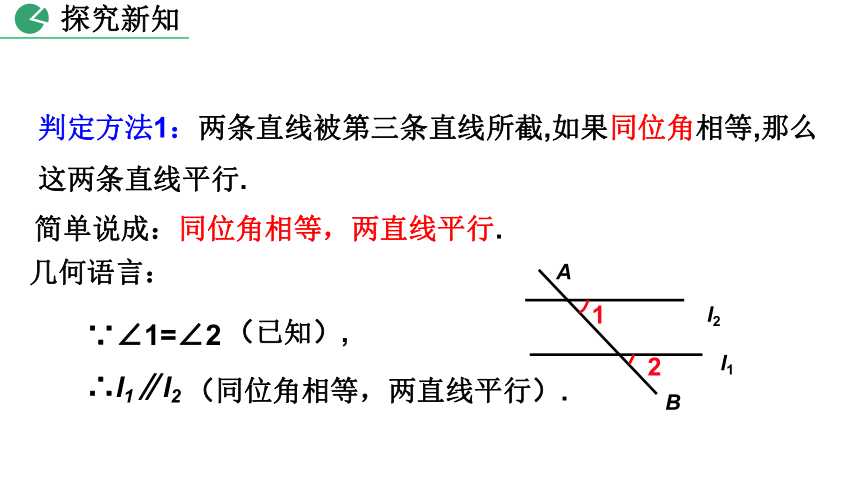
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
探究新知
(3)将其最初和最终的两种特殊位置抽象成几何图形:
1
2
l2
l1
A
B
(4) 由上面的操作过程,你能发现判定两直线平行的方法吗?
探究新知
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
几何语言:
∵∠1=∠2
∴l1∥l2
1
2
l2
l1
A
B
探究新知
(已知),
(同位角相等,两直线平行).
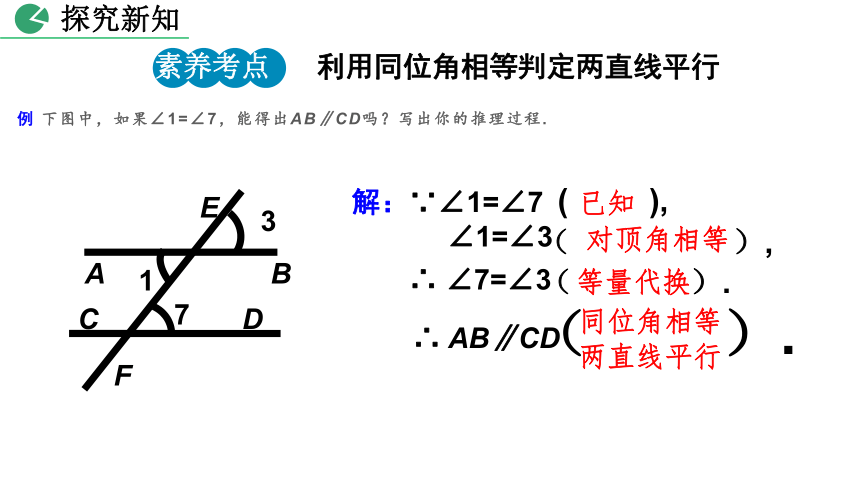
例 下图中,如果∠1=∠7,能得出AB∥CD吗?写出你的推理过程.
解:∵∠1=∠7
∠1=∠3
∴ ∠7=∠3
∴ AB∥CD
B
1
A
C
D
F
3
7
E
( ),
已知
( ),
对顶角相等
( ).
等量代换
( ).
同位角相等
两直线平行
探究新知
素养考点
利用同位角相等判定两直线平行
如图所示,∠1=∠2=35°,则AB与CD的关系是 ,
理由是 .
AB∥CD
同位角相等,两直线平行
巩固练习
变式训练
定理 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
这个定理可以简单说成:内错角相等,两直线平行.
你能运用所学知识来证实它是一个真命题吗?
探究新知
知识点 2
内错角相等两直线平行
已知: 如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.
求证: a∥b.
证明:∵ ∠1=∠2 ,
∠1=∠3 ,
∴∠2=∠3 ,
∴ a∥b .
(已知)
(对顶角相等)
(等量代换)
(同位角相等,两直线平行)
探究新知
判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠3=∠2(已知)
∴a∥b (内错角相等,两直线平行)
几何语言:
探究新知
2
b
a
1
3
例 完成下面证明:如图所示,CB平分∠ACD,∠1=∠3. 求证AB∥CD.
证明:∵CB平分∠ACD,∴∠1=∠2( ).
∵∠1=∠3,∴∠2=∠ .
∴AB∥CD( ).
角平分线的定义
3
内错角相等,两直线平行
探究新知
素养考点
利用内错角相等判定两直线平行
已知∠3=45 °,∠1与∠2互余,试说明AB//CD ?
解:∵∠1=∠2(对顶角相等),
∠1与∠2互余,
∴ ∠1+∠2=90°(已知).
∴∠1=∠2=45°.
∵ ∠3=45°(已知),
∴∠ 2=∠3.
∴ AB∥CD(内错角相等,两直线平行).
1
2
3
A
B
C
D
巩固练习
变式训练
c
a
1
b
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
条件是: ,
结论是: .
同旁内角互补
两直线平行
2
探究新知
知识点 3
利用同旁内角互补判定两直线平行
已知: 如图,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1与∠2互补.
求证: a∥b.
证明: ∵ ∠1与∠2互补
∴∠1+∠2=1800
又∵∠3+∠1=1800
∴∠2=∠3
∴ a∥b
(已知),
(两角互补的定义).
(平角的定义),
(同角的补角相等).
(同位角相等,两直线平行).
探究新知
判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
几何语言:
2
b
a
1
3
∵∠1+∠2=180°(已知),
∴a∥b(同旁内角互补,两直线平行).
探究新知
例 如图:直线AB、CD都和AE相交,且∠1+∠A=180? .求证:AB//CD.
证明:∵∠1+∠A=180?
C
B
A
D
2
1
E
3
∴∠2+∠A=180?
∴
( ),
( ).
( ).
已知
对顶角相等
等量代换
同旁内角互补,两直线平行
∠1=∠2 ( ),
AB∥CD
探究新知
利用同旁内角互补判定两直线平行
素养考点
① ∵ ∠2 = ∠ 6(已知),
∴ ___∥___( ).
② ∵ ∠3 = ∠5(已知),
∴ ___∥___( ).
③∵ ∠4 +___=180o(已知),
∴ ___∥___( ).
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
F
E
根据条件完成填空.
巩固练习
变式训练
蜂房的底部由三个全等的四边形围成,每个四边形的形状如右图所示,其中∠α=109°28′,∠β=70°32′,试确定这三个四边形的对边的位置关系,并说明你的理由.
答:这三个四边形的对边分别平行,因为∠α+∠β=180°,根据同旁内角互补,两直线平行.
巩固练习
变式训练
(2019?南京)结合图,用符号语言表达定理“同旁内角互补,
两直线平行”的推理形式:∵___________________,∴a∥b.
∠1+∠3=180°
连接中考
1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
C
1
2
3
A
E
B
C
D
课堂检测
基础巩固题
2.如图,已知∠1=30°,∠2或∠3满足条件 ,则a//b.
2
1
3
a
b
c
∠2=150°或∠3=30°
基础巩固题
课堂检测
3.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是__________________________.
(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
基础巩固题
课堂检测
(3)从∠ =∠ ,可以推出AD∥BC,理由是 _____________________ .
(4)从∠5=∠ ,可以推出AB∥CD, 理由是____________ .
2
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
基础巩固题
课堂检测
① ∵ ∠1 =____(已知),
∴ AB∥CE( ).
② ∵ ∠1 +_____=180o(已知),
∴CD∥BF( ).
③ ∵ ∠1 +∠5 =180o(已知),
∴ ___∥_____( ).
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB( )
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
4.根据条件完成填空.
基础巩固题
课堂检测
理由如下:
∵ AC平分∠DAB(已知),
∴ ∠1=∠2(角平分线定义).
又∵ ∠1= ∠3(已知),
∴ ∠2=∠3(等量代换).
∴ AB∥CD(内错角相等,两直线平行).
如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
能力提升题
课堂检测
∴ AB∥MN(内错角相等,两直线平行).
解:
∵ ∠MCA= ∠ A(已知),
又 ∵∠ DEC= ∠ B(已知),
∴ AB∥DE(同位角相等,两直线平行).
∴ DE∥MN(如果两条直线都和第三条直线平行,那 么这两条直线也互相平行).
如图,已知∠MCA= ∠ A, ∠ DEC= ∠ B,那么DE∥MN吗?为什么?
A
E
B
C
D
N
M
拓广探索题
课堂检测
DE∥MN.
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定示意图
判定
数量关系
位置关系
课堂小结
1
2
l2
l1
A
B
装修师傅随身只带了一个量角器,要判断一块破碎的玻璃板的上下两边是否平行,你能帮助他解决这个问题吗?
?
导入新知
2. 能根据“同位角相等,两直线平行”证明“内错角相等,两直线平行”,“同旁内角互补,两直线平行” 并能简单地应用这些结论
1. 初步了解证明的基本步骤和书写格式.
素养目标
3. 能够根据平行线的判定方法进行简单的推理.
●
一、放
二、靠
三、推
四、画
我们已经学习过用三角尺和直尺画平行线的方法.
探究新知
知识点 1
同位角相等两直线平行
b
A
2
1
a
B
(1)画图过程中,什么角始终保持相等?
(2)直线a,b位置关系如何?
探究新知
(3)将其最初和最终的两种特殊位置抽象成几何图形:
1
2
l2
l1
A
B
(4) 由上面的操作过程,你能发现判定两直线平行的方法吗?
探究新知
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
几何语言:
∵∠1=∠2
∴l1∥l2
1
2
l2
l1
A
B
探究新知
(已知),
(同位角相等,两直线平行).
例 下图中,如果∠1=∠7,能得出AB∥CD吗?写出你的推理过程.
解:∵∠1=∠7
∠1=∠3
∴ ∠7=∠3
∴ AB∥CD
B
1
A
C
D
F
3
7
E
( ),
已知
( ),
对顶角相等
( ).
等量代换
( ).
同位角相等
两直线平行
探究新知
素养考点
利用同位角相等判定两直线平行
如图所示,∠1=∠2=35°,则AB与CD的关系是 ,
理由是 .
AB∥CD
同位角相等,两直线平行
巩固练习
变式训练
定理 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
这个定理可以简单说成:内错角相等,两直线平行.
你能运用所学知识来证实它是一个真命题吗?
探究新知
知识点 2
内错角相等两直线平行
已知: 如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.
求证: a∥b.
证明:∵ ∠1=∠2 ,
∠1=∠3 ,
∴∠2=∠3 ,
∴ a∥b .
(已知)
(对顶角相等)
(等量代换)
(同位角相等,两直线平行)
探究新知
判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠3=∠2(已知)
∴a∥b (内错角相等,两直线平行)
几何语言:
探究新知
2
b
a
1
3
例 完成下面证明:如图所示,CB平分∠ACD,∠1=∠3. 求证AB∥CD.
证明:∵CB平分∠ACD,∴∠1=∠2( ).
∵∠1=∠3,∴∠2=∠ .
∴AB∥CD( ).
角平分线的定义
3
内错角相等,两直线平行
探究新知
素养考点
利用内错角相等判定两直线平行
已知∠3=45 °,∠1与∠2互余,试说明AB//CD ?
解:∵∠1=∠2(对顶角相等),
∠1与∠2互余,
∴ ∠1+∠2=90°(已知).
∴∠1=∠2=45°.
∵ ∠3=45°(已知),
∴∠ 2=∠3.
∴ AB∥CD(内错角相等,两直线平行).
1
2
3
A
B
C
D
巩固练习
变式训练
c
a
1
b
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
条件是: ,
结论是: .
同旁内角互补
两直线平行
2
探究新知
知识点 3
利用同旁内角互补判定两直线平行
已知: 如图,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1与∠2互补.
求证: a∥b.
证明: ∵ ∠1与∠2互补
∴∠1+∠2=1800
又∵∠3+∠1=1800
∴∠2=∠3
∴ a∥b
(已知),
(两角互补的定义).
(平角的定义),
(同角的补角相等).
(同位角相等,两直线平行).
探究新知
判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
几何语言:
2
b
a
1
3
∵∠1+∠2=180°(已知),
∴a∥b(同旁内角互补,两直线平行).
探究新知
例 如图:直线AB、CD都和AE相交,且∠1+∠A=180? .求证:AB//CD.
证明:∵∠1+∠A=180?
C
B
A
D
2
1
E
3
∴∠2+∠A=180?
∴
( ),
( ).
( ).
已知
对顶角相等
等量代换
同旁内角互补,两直线平行
∠1=∠2 ( ),
AB∥CD
探究新知
利用同旁内角互补判定两直线平行
素养考点
① ∵ ∠2 = ∠ 6(已知),
∴ ___∥___( ).
② ∵ ∠3 = ∠5(已知),
∴ ___∥___( ).
③∵ ∠4 +___=180o(已知),
∴ ___∥___( ).
AB
CD
AB
CD
∠5
AB
CD
A
C
1
4
2
3
5
8
6
7
B
D
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
F
E
根据条件完成填空.
巩固练习
变式训练
蜂房的底部由三个全等的四边形围成,每个四边形的形状如右图所示,其中∠α=109°28′,∠β=70°32′,试确定这三个四边形的对边的位置关系,并说明你的理由.
答:这三个四边形的对边分别平行,因为∠α+∠β=180°,根据同旁内角互补,两直线平行.
巩固练习
变式训练
(2019?南京)结合图,用符号语言表达定理“同旁内角互补,
两直线平行”的推理形式:∵___________________,∴a∥b.
∠1+∠3=180°
连接中考
1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
C
1
2
3
A
E
B
C
D
课堂检测
基础巩固题
2.如图,已知∠1=30°,∠2或∠3满足条件 ,则a//b.
2
1
3
a
b
c
∠2=150°或∠3=30°
基础巩固题
课堂检测
3.如图.(1)从∠1=∠4,可以推出 ∥ ,
理由是__________________________.
(2)从∠ABC +∠ =180°,可以推出AB∥CD ,
理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
基础巩固题
课堂检测
(3)从∠ =∠ ,可以推出AD∥BC,理由是 _____________________ .
(4)从∠5=∠ ,可以推出AB∥CD, 理由是____________ .
2
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
基础巩固题
课堂检测
① ∵ ∠1 =____(已知),
∴ AB∥CE( ).
② ∵ ∠1 +_____=180o(已知),
∴CD∥BF( ).
③ ∵ ∠1 +∠5 =180o(已知),
∴ ___∥_____( ).
AB
CE
∠2
④ ∵ ∠4 +_____=180o(已知)
∴ CE∥AB( )
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
4.根据条件完成填空.
基础巩固题
课堂检测
理由如下:
∵ AC平分∠DAB(已知),
∴ ∠1=∠2(角平分线定义).
又∵ ∠1= ∠3(已知),
∴ ∠2=∠3(等量代换).
∴ AB∥CD(内错角相等,两直线平行).
如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
能力提升题
课堂检测
∴ AB∥MN(内错角相等,两直线平行).
解:
∵ ∠MCA= ∠ A(已知),
又 ∵∠ DEC= ∠ B(已知),
∴ AB∥DE(同位角相等,两直线平行).
∴ DE∥MN(如果两条直线都和第三条直线平行,那 么这两条直线也互相平行).
如图,已知∠MCA= ∠ A, ∠ DEC= ∠ B,那么DE∥MN吗?为什么?
A
E
B
C
D
N
M
拓广探索题
课堂检测
DE∥MN.
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定示意图
判定
数量关系
位置关系
课堂小结
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
