教科2003课标版 必修1-2. 位置变化的描述——位移课件35张PPT
文档属性
| 名称 | 教科2003课标版 必修1-2. 位置变化的描述——位移课件35张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-28 08:03:32 | ||
图片预览










文档简介
第二节
位置变化的描述—位移
塔克拉玛干沙漠,布满了起伏的沙丘,被称为“死亡之海”
我在哪里?我要去的地方在哪里?选哪条路线最佳?
许多穿越塔克拉玛于沙漠的勇士常常迷路,因此而丧生,
20世纪末一位欧州妇女成功地穿越了这个“死亡之海”。
这是因为她携带了GPS接收机,
解决了三个问题:我在哪里?我要去的地方在哪里?选哪条路线最佳?
本节我们学习描述物体运动的物理量:位置、位移和路程。
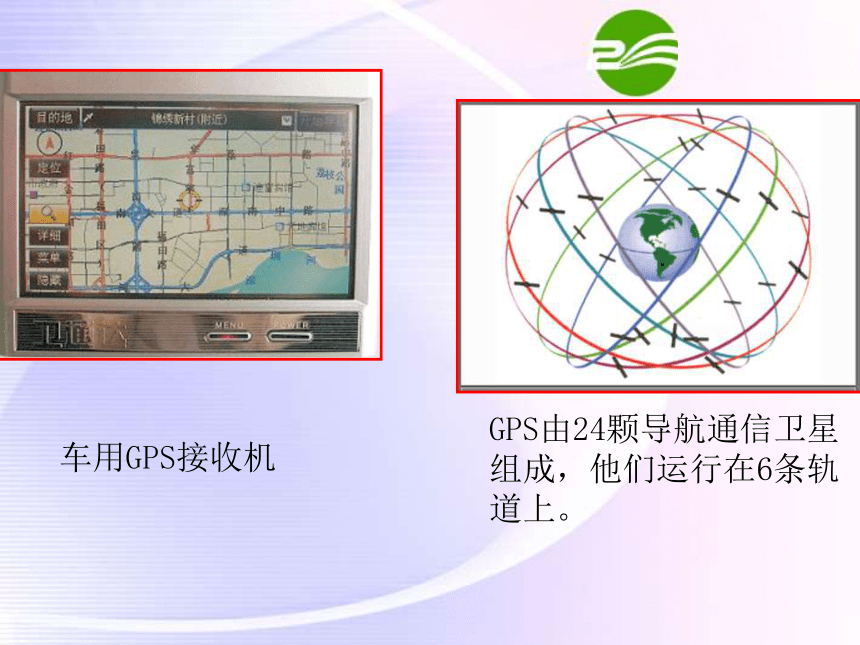
车用GPS接收机
GPS由24颗导航通信卫星组成,他们运行在6条轨道上。
[思考]
某运动员正在百米赛道上自南向北全力奔跑,为准确描述他在不同时刻的位置和位置变化,应建立怎样的坐标系?
提示:百米赛道为直线跑道,可以以赛道起点为原点,选择向北方向为正方向,选取一定的标度,建立一维直线坐标系.
如何确定物体位置 ?
? 文字描述方便吗?能精确吗?
? 有没有简便又准确的方法?
区分:定性与定量
笛卡儿发明坐标系
若物体只在一条直线上运动,如何描述位置变化?
一、坐标系
1、坐标系建立的作用:定量描述质点的位置及位置的变化.
2、坐标系的构成要素:
原点、正方向、标度、 物理量、单位
?思维体操
X1、X2的位置是多少?
X1
X2
? 对于在平面上运动的物体,例如大海中的轮船,要描述它的位置及其位置的变化,你认为应该怎样建立坐标系?
完成P7的“讨论与交流”
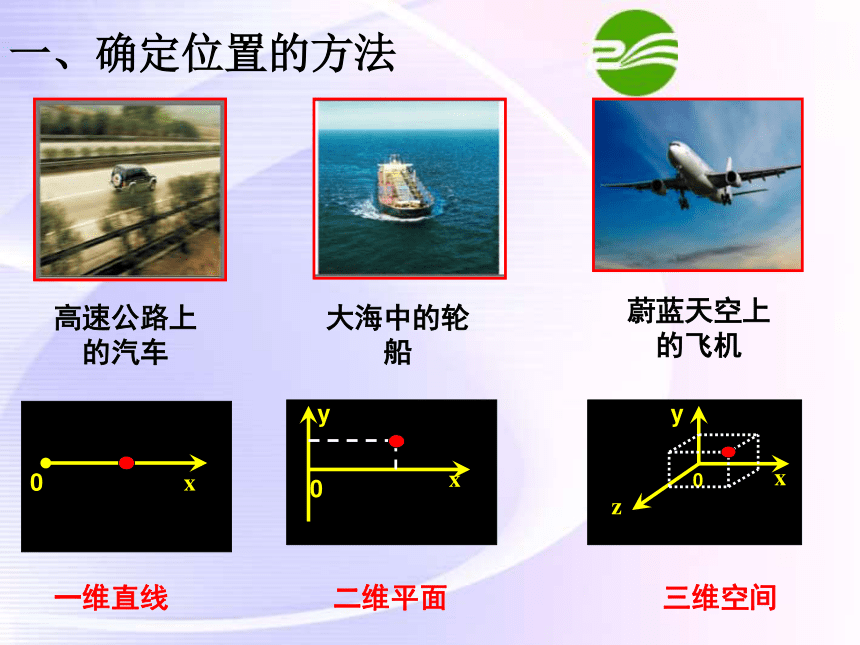
一、确定位置的方法
高速公路上的汽车
大海中的轮船
蔚蓝天空上的飞机
0
x
0
x
y
0
x
y
z
一维直线
二维平面
三维空间
如何在地面定物体位置?
寻找有用信息:经度与纬度(大地坐标系)
生活中的物理
GPS:全球定位系统
( 授时与测距导航系统----全球定位系统)
全球定位系统是美国从20世纪70年代开始研制,历时20年,耗资200亿美元,于1994年全面建成,具有在海、陆、空进行全方位实时三维导航与定位能力的新一代卫星导航与定位系统。
在美国,GPS全球卫星定位技术与“阿波罗”飞船登月、航天飞机升空,同列为20世纪“三大航天工程”。
生活中的物理
GPS:全球定位系统
GPS系统包括三大部分:
(1)GPS卫星(空间部分)
(2)地面支撑系统(地面监控部分)
(3)GPS接收机(用户部分)
定位仪中所示位置:
24颗GPS卫星在离地面1万2千公里的高空上,以12小时的周期环绕地球运行,使得在任意时刻,在地面上的任意一点都可以同时观测到4颗以上的卫星。
由于卫星的位置精确可知,在GPS观测中,我们可得到卫星到接收机的距离,利用三维坐标中的距离公式,利用3颗卫星,就可以组成3个方程式,解出观测点的位置(X,Y,Z)。考虑到卫星的时钟与接收机时钟之间的误差,实际上有4个未知数,X、Y、Z和钟差,因而需要引入第4颗卫星,形成4个方程式进行求解,从而得到观测点的经纬度和高度。
事实上,接收机往往可以锁住4颗以上的卫星,这时,接收机可按卫星的星座分布分成若干组,每组4颗,然后通过算法挑选出误差最小的一组用作定位,从而提高精度。
由于卫星运行轨道、卫星时钟存在误差,大气对流层、电离层对信号的影响,以及人为的SA保护政策,使得民用GPS的定位精度只有100米。为提高定位精度,普遍采用差分GPS(DGPS)技术,建立基准站(差分台)进行GPS观测,利用已知的基准站精确坐标,与观测值进行比较,从而得出一修正数,并对外发布。接收机收到该修正数后,与自身的观测值进行比较,消去大部分误差,得到一个比较准确的位置。实验表明,利用差分GPS,定位精度可提高到5米。
【典例1】小明所在学校的校门口是朝南的,他进入校门后一直向前走120米后,再向东走40米就到了他所在的教室,请你画出他的教室所在的位置.
[解析]选校门口为坐标原点,x轴正方向表示向东,y轴正方向表示向北,以1 cm长的线段表示40 m,建立坐标系如图所示,小明的教室在坐标为(40 m,120 m)处.
[思路点拨]
物体在一段时间内位置变化
平原春色
长城垛口
物体在一段时间内位置变化-----位移
物体从A运动到B,不管沿着什么轨迹,它的位移都是一样的。这个位移可以用一条有方向的(箭头)线段AB表示
y
O
x
A
B
3.特别:直线运动的位置和位移:只需建立直线坐标系.用坐标表示位置,用坐标的变化量表示位移.如图所示,物体在时刻t1处于“位置”x1,在时刻t2运动到“位置”x2.那么,位移为Δx=x2-x1.
二、位移
1.定义:物体在一段时间内位置的变化称为位移
2.表示:从初位置到末位置的一条有向线段
三、矢量和标量
标量:
在物理学中,只有大小而没有方向的物理量叫标量,如:质量、温度、时间、路程
矢量:
在物理学中,既有大小又有方向的物理量叫矢量,如:力、位移、速度
三、矢量和标量
1.矢量的表示方法
(1)图示表示:用带箭头的线段表示,线段的长度表示矢量的大小,箭头的方向表示矢量的方向.
(2)数字表示:先建立坐标系并规定正方向,然后用正负数来表示矢量,“+”号表示与坐标系规定的正方向一致,“-”号表示与坐标系规定的正方向相反;数字的大小表示矢量的大小.
2.矢量和标量的区别
(1)矢量有方向,标量没有方向.
(2)标量的运算法则为算术运算法则,即初中所学的加、减、乘、除等运算方法;矢量的运算法则为以后要学到的平行四边形定则.
(3)矢量大小的比较要看其数值的绝对值大小,绝对值大的矢量大,而“-”只代表方向.
西单
国家大剧院
人民大会堂
天安门
天安门广场
王府井
长安街
N
A
O
B
1.8km
1.2km
解:王府井到西单
△x1=XB-XA=1.8-(-1.2km)=3.0km
方向向西
西单到王府井
△x2=XA-XB=(-1.2km)-1.8=-3.0km
方向向东
注意:负号只表示方向!不表示大小!
课本P7例题:
西单
国家大剧院
人民大会堂
天安门
天安门广场
王府井
长安街
N
A
O
B
1.8km
1.2km
O
x/km
1.8
3.0
解:王府井到西单
△x1==0-3.0km=-3.0km
方向向西
西单到王府井
△x2==3.0km-0=3.0km
方向向东
变
注意:负号只表示方向!不表示大小!
解题规范
[思考]
在400 m运动场上举行的运动会中:一位同学沿着400 m的跑道跑一圈,他的位移和路程是多少呢?
提示:沿着400 m的跑道跑一圈的同学,位移是0,路程是400 m.
2.位移与路程的区别
(1)位移表示质点位置的变化的物理量(精确) 路程则是表示质点通过的实际轨迹长度的物理量(只能粗略描述质点位置的变化)
(3) 位移与质点的运动路径无关,只与初位置、末位置有关. 路程不仅与质点的初末位置有关,还与路径有关
(2)位移是矢量(即有大小又有方向)
大小为有向线段的长度,方向为有向线段的方向
路程是标量(只有大小没有方向)
只有当质点做单向直线运动时,位移的大小才等于路程
思考:什么情况下,质点的位移大小等于路程?
位移和路程
路程
位移
区别
意义
表示运动轨迹的长度
表示位置变化的大小和方向
大小
轨迹的长度
从初位置到末位置的有向线段的长度
方向
无方向
从初位置指向末位置
图示(物体沿曲线由A运动到B)
曲线AB的长度
由A到B的有向线段
联系
(1)两者单位相同,都是米(m)
(2)位移的大小小于等于路程,在单向直线运动中,位移的大小等于路程
练一练:
小球从距地面5m高处落下,碰到地面反 弹后,在距地面2m高处被接住,则小球从高处落下到被接住这一过程中通过的路程和位移的大小分别是( )
A、7m、7m B、5m、2m
C、5m、3m D、7m、3m
D
A
B
C
思考与讨论 :
如图,小华从A点向正北出发,走到B点后转向正东走到达C点,已知A到B的距离为4m,B到C的距离为3m,则小华从A到C的路程和位移各是多少?
【典例2】一个人晨练,按如图所示,走半径为R的中国古代的八卦图运动,中央的S部分是两个直径为R的半圆.他从A点出发沿曲线ABCOADC行进.求:
(1)他从A点第一次走到O点时的位移的大小和方向;
(2)他从A点第一次走到D点时的位移和路程.
[思路点拨] (1)路程是运动轨迹的长度,而位移为始末位置间的有向线段.
(2)求位移时要求出位移的大小和方向.
(1)从A点第一次走到O点时的位移的大小等于线段AO的长度,即x1=R.位移的方向为由北指向南.
(2)从A点第一次走到D点时的位移的大小等于线段AD的长度,即x2= R.位移的方向为东偏南45°.从A点第一次走到D点时的路程等于整个运动轨迹的长度,即s= ×2πR+2π× = πR.
练习:
有一质点在X轴上运动,已知各时刻质点位置如图
X/m
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
t=3s
t=1s
t=2s
t=4s
t=0s
t=5s
S3=17m
①质点在3s 内的路程;
②质点在前3s内的位移
③质点在第3s内的位移
④质点在___s内位移最大
⑤质点在第___s内位移最大
ΔX3=-1m
ΔXⅢ=3m
4
2
ΔX4=-7m
ΔXⅡ=-9m
科学思维——数形结合思想在物理中的应用
在物理学中,表达物理概念和物理规律有其特有的科学思维和科学方法,如表达物体的位置变化.生活中可能更多的是对自然运动的静观、思辨的一种定性的表达,而物理学科则是对运动做定量的数学推演,甚至要设计实验来验证.
为了定量地描述物体的位置及位置的变化,需要运用数形结合思想,如在参考系的基础上建立适当的坐标系,有时候为了描述空间的位置更具体,建立坐标系时,还要借助时刻和时间等.
湖中O点有一观察站,一小船从O点出发向东行驶4 km,又向北行驶3 km.(已知sin 37°=0.6).(1)建立一个适当的坐标系,在坐标系中标出小船的初位置和末位置.(2)在O点的观察员对小船位置的报告最为精确的是( )
A.小船的位置离O点7 km
B.小船向东北方向运动了7 km
C.小船向东北方向运动了5 km
D.小船的位置在东偏北37°方
向距O点5 km处
1、学习了如何利用坐标系来描述物体的位置和位置变化。
课后作业:课时作业(二)
课堂小结
2、知道了位移及位移与路程的区别。
3、知道了什么是标量和矢量。
位置变化的描述—位移
塔克拉玛干沙漠,布满了起伏的沙丘,被称为“死亡之海”
我在哪里?我要去的地方在哪里?选哪条路线最佳?
许多穿越塔克拉玛于沙漠的勇士常常迷路,因此而丧生,
20世纪末一位欧州妇女成功地穿越了这个“死亡之海”。
这是因为她携带了GPS接收机,
解决了三个问题:我在哪里?我要去的地方在哪里?选哪条路线最佳?
本节我们学习描述物体运动的物理量:位置、位移和路程。
车用GPS接收机
GPS由24颗导航通信卫星组成,他们运行在6条轨道上。
[思考]
某运动员正在百米赛道上自南向北全力奔跑,为准确描述他在不同时刻的位置和位置变化,应建立怎样的坐标系?
提示:百米赛道为直线跑道,可以以赛道起点为原点,选择向北方向为正方向,选取一定的标度,建立一维直线坐标系.
如何确定物体位置 ?
? 文字描述方便吗?能精确吗?
? 有没有简便又准确的方法?
区分:定性与定量
笛卡儿发明坐标系
若物体只在一条直线上运动,如何描述位置变化?
一、坐标系
1、坐标系建立的作用:定量描述质点的位置及位置的变化.
2、坐标系的构成要素:
原点、正方向、标度、 物理量、单位
?思维体操
X1、X2的位置是多少?
X1
X2
? 对于在平面上运动的物体,例如大海中的轮船,要描述它的位置及其位置的变化,你认为应该怎样建立坐标系?
完成P7的“讨论与交流”
一、确定位置的方法
高速公路上的汽车
大海中的轮船
蔚蓝天空上的飞机
0
x
0
x
y
0
x
y
z
一维直线
二维平面
三维空间
如何在地面定物体位置?
寻找有用信息:经度与纬度(大地坐标系)
生活中的物理
GPS:全球定位系统
( 授时与测距导航系统----全球定位系统)
全球定位系统是美国从20世纪70年代开始研制,历时20年,耗资200亿美元,于1994年全面建成,具有在海、陆、空进行全方位实时三维导航与定位能力的新一代卫星导航与定位系统。
在美国,GPS全球卫星定位技术与“阿波罗”飞船登月、航天飞机升空,同列为20世纪“三大航天工程”。
生活中的物理
GPS:全球定位系统
GPS系统包括三大部分:
(1)GPS卫星(空间部分)
(2)地面支撑系统(地面监控部分)
(3)GPS接收机(用户部分)
定位仪中所示位置:
24颗GPS卫星在离地面1万2千公里的高空上,以12小时的周期环绕地球运行,使得在任意时刻,在地面上的任意一点都可以同时观测到4颗以上的卫星。
由于卫星的位置精确可知,在GPS观测中,我们可得到卫星到接收机的距离,利用三维坐标中的距离公式,利用3颗卫星,就可以组成3个方程式,解出观测点的位置(X,Y,Z)。考虑到卫星的时钟与接收机时钟之间的误差,实际上有4个未知数,X、Y、Z和钟差,因而需要引入第4颗卫星,形成4个方程式进行求解,从而得到观测点的经纬度和高度。
事实上,接收机往往可以锁住4颗以上的卫星,这时,接收机可按卫星的星座分布分成若干组,每组4颗,然后通过算法挑选出误差最小的一组用作定位,从而提高精度。
由于卫星运行轨道、卫星时钟存在误差,大气对流层、电离层对信号的影响,以及人为的SA保护政策,使得民用GPS的定位精度只有100米。为提高定位精度,普遍采用差分GPS(DGPS)技术,建立基准站(差分台)进行GPS观测,利用已知的基准站精确坐标,与观测值进行比较,从而得出一修正数,并对外发布。接收机收到该修正数后,与自身的观测值进行比较,消去大部分误差,得到一个比较准确的位置。实验表明,利用差分GPS,定位精度可提高到5米。
【典例1】小明所在学校的校门口是朝南的,他进入校门后一直向前走120米后,再向东走40米就到了他所在的教室,请你画出他的教室所在的位置.
[解析]选校门口为坐标原点,x轴正方向表示向东,y轴正方向表示向北,以1 cm长的线段表示40 m,建立坐标系如图所示,小明的教室在坐标为(40 m,120 m)处.
[思路点拨]
物体在一段时间内位置变化
平原春色
长城垛口
物体在一段时间内位置变化-----位移
物体从A运动到B,不管沿着什么轨迹,它的位移都是一样的。这个位移可以用一条有方向的(箭头)线段AB表示
y
O
x
A
B
3.特别:直线运动的位置和位移:只需建立直线坐标系.用坐标表示位置,用坐标的变化量表示位移.如图所示,物体在时刻t1处于“位置”x1,在时刻t2运动到“位置”x2.那么,位移为Δx=x2-x1.
二、位移
1.定义:物体在一段时间内位置的变化称为位移
2.表示:从初位置到末位置的一条有向线段
三、矢量和标量
标量:
在物理学中,只有大小而没有方向的物理量叫标量,如:质量、温度、时间、路程
矢量:
在物理学中,既有大小又有方向的物理量叫矢量,如:力、位移、速度
三、矢量和标量
1.矢量的表示方法
(1)图示表示:用带箭头的线段表示,线段的长度表示矢量的大小,箭头的方向表示矢量的方向.
(2)数字表示:先建立坐标系并规定正方向,然后用正负数来表示矢量,“+”号表示与坐标系规定的正方向一致,“-”号表示与坐标系规定的正方向相反;数字的大小表示矢量的大小.
2.矢量和标量的区别
(1)矢量有方向,标量没有方向.
(2)标量的运算法则为算术运算法则,即初中所学的加、减、乘、除等运算方法;矢量的运算法则为以后要学到的平行四边形定则.
(3)矢量大小的比较要看其数值的绝对值大小,绝对值大的矢量大,而“-”只代表方向.
西单
国家大剧院
人民大会堂
天安门
天安门广场
王府井
长安街
N
A
O
B
1.8km
1.2km
解:王府井到西单
△x1=XB-XA=1.8-(-1.2km)=3.0km
方向向西
西单到王府井
△x2=XA-XB=(-1.2km)-1.8=-3.0km
方向向东
注意:负号只表示方向!不表示大小!
课本P7例题:
西单
国家大剧院
人民大会堂
天安门
天安门广场
王府井
长安街
N
A
O
B
1.8km
1.2km
O
x/km
1.8
3.0
解:王府井到西单
△x1==0-3.0km=-3.0km
方向向西
西单到王府井
△x2==3.0km-0=3.0km
方向向东
变
注意:负号只表示方向!不表示大小!
解题规范
[思考]
在400 m运动场上举行的运动会中:一位同学沿着400 m的跑道跑一圈,他的位移和路程是多少呢?
提示:沿着400 m的跑道跑一圈的同学,位移是0,路程是400 m.
2.位移与路程的区别
(1)位移表示质点位置的变化的物理量(精确) 路程则是表示质点通过的实际轨迹长度的物理量(只能粗略描述质点位置的变化)
(3) 位移与质点的运动路径无关,只与初位置、末位置有关. 路程不仅与质点的初末位置有关,还与路径有关
(2)位移是矢量(即有大小又有方向)
大小为有向线段的长度,方向为有向线段的方向
路程是标量(只有大小没有方向)
只有当质点做单向直线运动时,位移的大小才等于路程
思考:什么情况下,质点的位移大小等于路程?
位移和路程
路程
位移
区别
意义
表示运动轨迹的长度
表示位置变化的大小和方向
大小
轨迹的长度
从初位置到末位置的有向线段的长度
方向
无方向
从初位置指向末位置
图示(物体沿曲线由A运动到B)
曲线AB的长度
由A到B的有向线段
联系
(1)两者单位相同,都是米(m)
(2)位移的大小小于等于路程,在单向直线运动中,位移的大小等于路程
练一练:
小球从距地面5m高处落下,碰到地面反 弹后,在距地面2m高处被接住,则小球从高处落下到被接住这一过程中通过的路程和位移的大小分别是( )
A、7m、7m B、5m、2m
C、5m、3m D、7m、3m
D
A
B
C
思考与讨论 :
如图,小华从A点向正北出发,走到B点后转向正东走到达C点,已知A到B的距离为4m,B到C的距离为3m,则小华从A到C的路程和位移各是多少?
【典例2】一个人晨练,按如图所示,走半径为R的中国古代的八卦图运动,中央的S部分是两个直径为R的半圆.他从A点出发沿曲线ABCOADC行进.求:
(1)他从A点第一次走到O点时的位移的大小和方向;
(2)他从A点第一次走到D点时的位移和路程.
[思路点拨] (1)路程是运动轨迹的长度,而位移为始末位置间的有向线段.
(2)求位移时要求出位移的大小和方向.
(1)从A点第一次走到O点时的位移的大小等于线段AO的长度,即x1=R.位移的方向为由北指向南.
(2)从A点第一次走到D点时的位移的大小等于线段AD的长度,即x2= R.位移的方向为东偏南45°.从A点第一次走到D点时的路程等于整个运动轨迹的长度,即s= ×2πR+2π× = πR.
练习:
有一质点在X轴上运动,已知各时刻质点位置如图
X/m
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
t=3s
t=1s
t=2s
t=4s
t=0s
t=5s
S3=17m
①质点在3s 内的路程;
②质点在前3s内的位移
③质点在第3s内的位移
④质点在___s内位移最大
⑤质点在第___s内位移最大
ΔX3=-1m
ΔXⅢ=3m
4
2
ΔX4=-7m
ΔXⅡ=-9m
科学思维——数形结合思想在物理中的应用
在物理学中,表达物理概念和物理规律有其特有的科学思维和科学方法,如表达物体的位置变化.生活中可能更多的是对自然运动的静观、思辨的一种定性的表达,而物理学科则是对运动做定量的数学推演,甚至要设计实验来验证.
为了定量地描述物体的位置及位置的变化,需要运用数形结合思想,如在参考系的基础上建立适当的坐标系,有时候为了描述空间的位置更具体,建立坐标系时,还要借助时刻和时间等.
湖中O点有一观察站,一小船从O点出发向东行驶4 km,又向北行驶3 km.(已知sin 37°=0.6).(1)建立一个适当的坐标系,在坐标系中标出小船的初位置和末位置.(2)在O点的观察员对小船位置的报告最为精确的是( )
A.小船的位置离O点7 km
B.小船向东北方向运动了7 km
C.小船向东北方向运动了5 km
D.小船的位置在东偏北37°方
向距O点5 km处
1、学习了如何利用坐标系来描述物体的位置和位置变化。
课后作业:课时作业(二)
课堂小结
2、知道了位移及位移与路程的区别。
3、知道了什么是标量和矢量。
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
