2020-2021学年度 苏科版九年级下学期 第六章图形的相似试卷( word无答案)
文档属性
| 名称 | 2020-2021学年度 苏科版九年级下学期 第六章图形的相似试卷( word无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 527.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览


文档简介
九年级数学--第六章测试卷
班级___________姓名___________得分___________
一、选择题:(本题共10小题,每小题3分,共30分)
1.若=,则的值为( )
A.1
B.
C.
D.
2.已知线段a、b、c,其中c是a、b的比例中项,若a=9cm,b=4cm,则线段c长( )
A.18cm
B.5cm
C.6cm
D.±6cm
3.已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是( )
A.
B.
C.
D.
4.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C
B.∠APB=∠ABC
C.
=
D.
=
5.如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( )
A.4
B.7
C.3
D.12
6.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2)
B.(1,1)
C.(,)
D.(2,1)
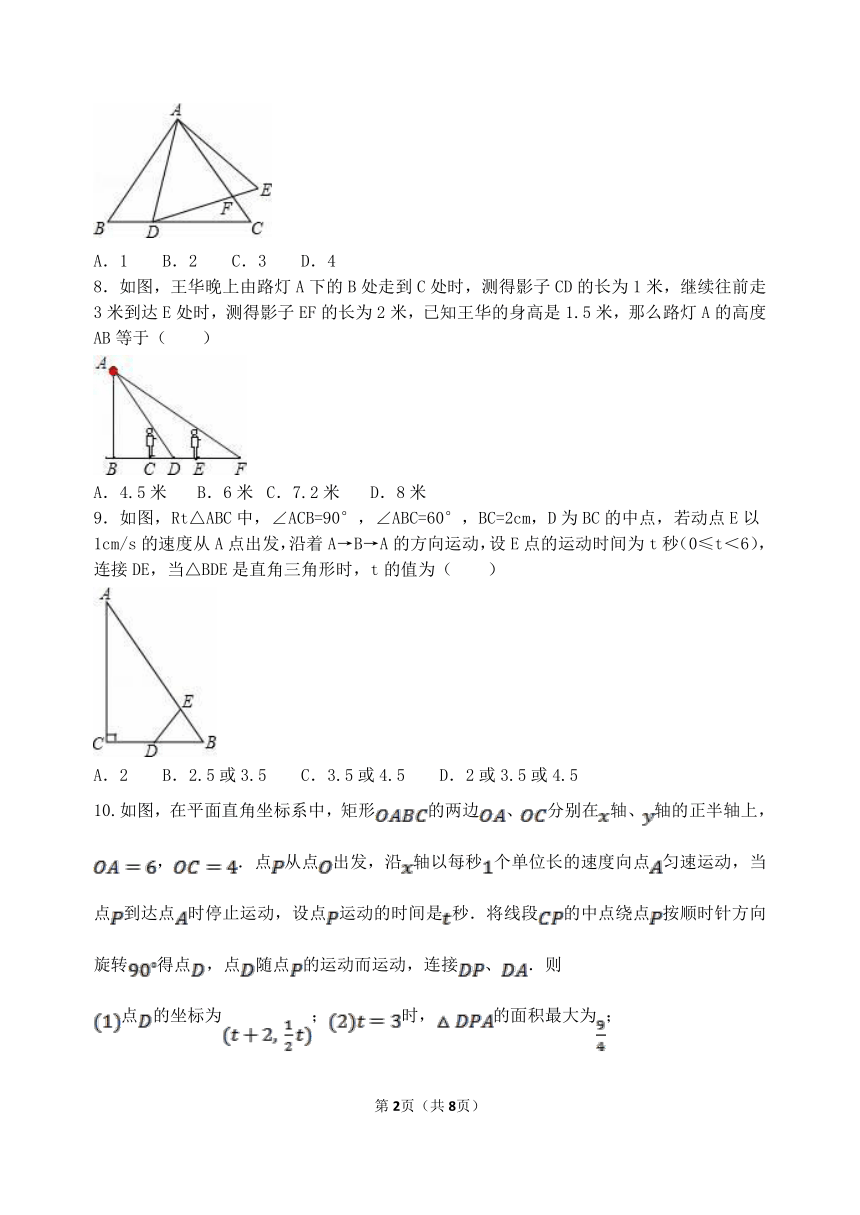
7.如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( )
A.1
B.2
C.3
D.4
8.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB等于( )
A.4.5米
B.6米
C.7.2米
D.8米
9.如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
A.2
B.2.5或3.5
C.3.5或4.5
D.2或3.5或4.5
10.如图,在平面直角坐标系中,矩形的两边、分别在轴、轴的正半轴上,,.点从点出发,沿轴以每秒个单位长的速度向点匀速运动,当点到达点时停止运动,设点运动的时间是秒.将线段的中点绕点按顺时针方向旋转得点,点随点的运动而运动,连接、.则
点的坐标为;时,的面积最大为;
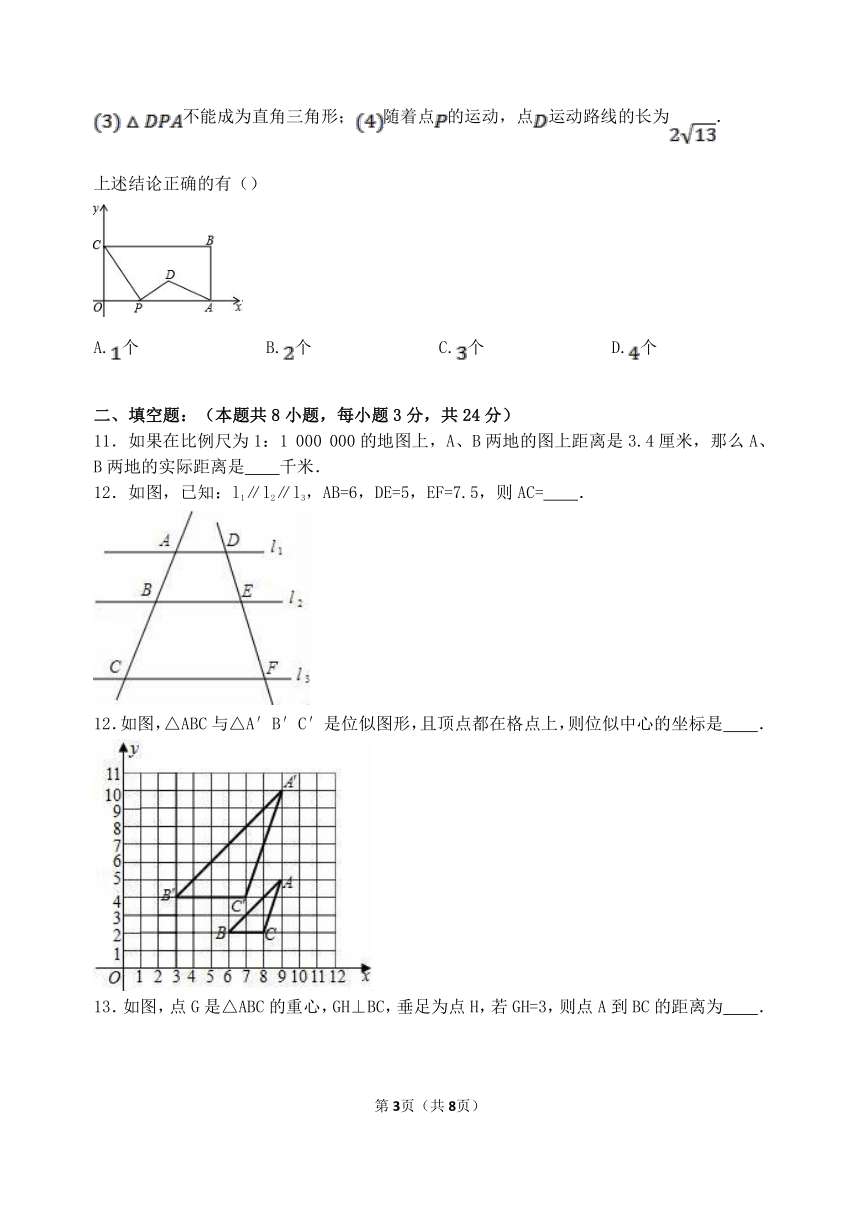
不能成为直角三角形;随着点的运动,点运动路线的长为.
上述结论正确的有()
A.个
B.个
C.个
D.个
二、填空题:(本题共8小题,每小题3分,共24分)
11.如果在比例尺为1:1
000
000的地图上,A、B两地的图上距离是3.4厘米,那么A、B两地的实际距离是 千米.
12.如图,已知:l1∥l2∥l3,AB=6,DE=5,EF=7.5,则AC= .
12.如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是 .
13.如图,点G是△ABC的重心,GH⊥BC,垂足为点H,若GH=3,则点A到BC的距离为 .
14.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB= m.
15.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为 时,△ADP和△ABC相似.
16.如图,双曲线y=经过Rt△BOC斜边上的点A,且满足=,与BC交于点D,S△BOD=21,求k= .
17.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=S△FGH;④AG+DF=FG.
其中正确的是 .(把所有正确结论的序号都选上)
三、解答题:(本大题共10大题,共76分)
18.如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E.
(1)求证:△ADE∽△MAB;
(2)求DE的长.
19.如图,△ABC中,CD是边AB上的高,且=.
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
20.在锐角△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,BC=15cm,BC边上的高是10cm,求正方形的面积.
21.已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.
22.如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?
23.如图,点A(1,4)、B(2,a)在函数y=(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
24.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
25.已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点0.点P从点A出发,沿方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:
(1)当t为何值时,△AOP是等腰三角形?
(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形S五边形OECQF:S△ACD=9:16?若存在,求出t的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.
26.定义:如图,点,把线段分割成,和,若以,,为边的三角形是一个直角三角形,则称点,是线段的勾股分割点.
已知点,是线段的勾股分割点,若,,求的长;
如图,在中,是中位线,点,是线段的勾股分割点,且,连接,分别交于点,,求证:点,是线段的勾股分割点;
已知点是线段上的一定点,其位置如图所示,请在上画一点,使点,是线段的勾股分割点(要求尺规作图,保留作图痕迹,画一种情形即可);
如图,已知点,是线段的勾股分割点,,,和均为等边三角形,分别交,,于点,,,若是的中点,试探究,和的数量关系,并说明理由.
第4页(共40页)
班级___________姓名___________得分___________
一、选择题:(本题共10小题,每小题3分,共30分)
1.若=,则的值为( )
A.1
B.
C.
D.
2.已知线段a、b、c,其中c是a、b的比例中项,若a=9cm,b=4cm,则线段c长( )
A.18cm
B.5cm
C.6cm
D.±6cm
3.已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是( )
A.
B.
C.
D.
4.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C
B.∠APB=∠ABC
C.
=
D.
=
5.如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( )
A.4
B.7
C.3
D.12
6.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2)
B.(1,1)
C.(,)
D.(2,1)
7.如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( )
A.1
B.2
C.3
D.4
8.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB等于( )
A.4.5米
B.6米
C.7.2米
D.8米
9.如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
A.2
B.2.5或3.5
C.3.5或4.5
D.2或3.5或4.5
10.如图,在平面直角坐标系中,矩形的两边、分别在轴、轴的正半轴上,,.点从点出发,沿轴以每秒个单位长的速度向点匀速运动,当点到达点时停止运动,设点运动的时间是秒.将线段的中点绕点按顺时针方向旋转得点,点随点的运动而运动,连接、.则
点的坐标为;时,的面积最大为;
不能成为直角三角形;随着点的运动,点运动路线的长为.
上述结论正确的有()
A.个
B.个
C.个
D.个
二、填空题:(本题共8小题,每小题3分,共24分)
11.如果在比例尺为1:1
000
000的地图上,A、B两地的图上距离是3.4厘米,那么A、B两地的实际距离是 千米.
12.如图,已知:l1∥l2∥l3,AB=6,DE=5,EF=7.5,则AC= .
12.如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是 .
13.如图,点G是△ABC的重心,GH⊥BC,垂足为点H,若GH=3,则点A到BC的距离为 .
14.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB= m.
15.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为 时,△ADP和△ABC相似.
16.如图,双曲线y=经过Rt△BOC斜边上的点A,且满足=,与BC交于点D,S△BOD=21,求k= .
17.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=S△FGH;④AG+DF=FG.
其中正确的是 .(把所有正确结论的序号都选上)
三、解答题:(本大题共10大题,共76分)
18.如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E.
(1)求证:△ADE∽△MAB;
(2)求DE的长.
19.如图,△ABC中,CD是边AB上的高,且=.
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.
20.在锐角△ABC中,正方形EFGH的两个顶点E、F在BC上,另两个顶点G、H分别在AC、AB上,BC=15cm,BC边上的高是10cm,求正方形的面积.
21.已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.
22.如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?
23.如图,点A(1,4)、B(2,a)在函数y=(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
24.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
25.已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点0.点P从点A出发,沿方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:
(1)当t为何值时,△AOP是等腰三角形?
(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形S五边形OECQF:S△ACD=9:16?若存在,求出t的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.
26.定义:如图,点,把线段分割成,和,若以,,为边的三角形是一个直角三角形,则称点,是线段的勾股分割点.
已知点,是线段的勾股分割点,若,,求的长;
如图,在中,是中位线,点,是线段的勾股分割点,且,连接,分别交于点,,求证:点,是线段的勾股分割点;
已知点是线段上的一定点,其位置如图所示,请在上画一点,使点,是线段的勾股分割点(要求尺规作图,保留作图痕迹,画一种情形即可);
如图,已知点,是线段的勾股分割点,,,和均为等边三角形,分别交,,于点,,,若是的中点,试探究,和的数量关系,并说明理由.
第4页(共40页)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
