人教版数学九年级上册课件:22.1.3二次函数y=a(x-h)2的图象和性质(18张PPT)
文档属性
| 名称 | 人教版数学九年级上册课件:22.1.3二次函数y=a(x-h)2的图象和性质(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
22.1.3 二次函数 y=a(x-h) +k
的图象和性质(第2课时)
第二十二章 二次函数
二次函数 y=a(x-h) 的图象和性质
y=ax2+k
y=ax2
复习旧知,引入新课
a>0
a<0
上下平移
个单位
k>0
k<0
k<0
k>0
问题 函数 , 的图象,能否也可以由函数 平移得到?
复习旧知,引入新课
讲授新课
互动探究
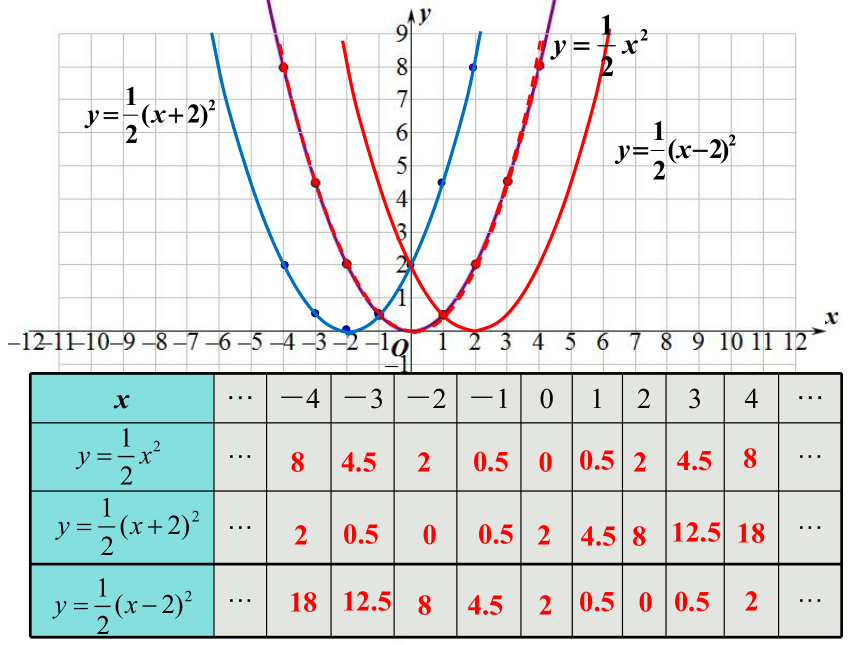
例1.在如图所示的坐标系中,画出二次函数 ,
与 的图象.
解:先列表:
x ··· -4 -3 -2 -1 0 1 2 3 4 ···
··· ···
··· ···
··· ···
x ··· -4 -3 -2 -1 0 1 2 3 4 ···
··· ···
··· ···
··· ···
8
8
4.5
4.5
0.5
0.5
4.5
8
12.5
18
0.5
0.5
2
0
2
2
0
2
4.5
8
12.5
18
0.5
0.5
2
0
2
观察探究 得出新知
左加
右减
二次函数y=ax2与y=a(x-h)2的关系
一
平移规律: 对解析式中自变量 “左加右减”
开口方向 向上 向上 向上
顶点坐标 (-2,0) (0,0) (2,0)
对称轴 直线x=-2 直线x=0 直线x=2
最值 y最小值=0 y最小值=0 y最小值=0
增减性 当x <-2时,
y随x的↑而↓;
x >-2时,
y随x的↑而↑. 当x < 0时,
y随x的↑而↓;
x > 0时,
y随x的↑而↑. 当x < 2时,
y随x的↑而↓;
x > 2时,
y随x的↑而↑.
二次函数y=ax2与y=a(x-h)2的图象和性质
一
二次函数y=ax2与y=a(x-h)2的关系
一
例2.抛物线 , 与抛物线 有什么关系?
-2
2
-2
-4
-6
4
-4
想一想
左加
右减
巩固练习
(1)
(2)
(3)
(4)
(5)
向左平移5个单位
向右平移3个单位
?
?
向左平移2个单位
?
?
向右平移1个单位
练习1.请根据题意填空
向上平移2个单位
?
练习2:不画图象,直接说出下列抛物线的开口方向、顶点坐标及对称轴
(1)
(2)
向上,(3,0),直线x=3
向下,(﹣2,0),直线x=﹣2
练习3:
向右平移 个单位
向左平移 个单位
思考:二次函数 与 有什么关系?
练习4. 抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式.
解:二次函数y=ax2的图象向右平移3个单位后的二次函数关系式可表示为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2, ,
∴平移后二次函数关系式为y= (x-3)2.
方法总结:根据抛物线左右平移的规律,向右平移3个单位后,a不变,括号内应“减去3”;若向左平移3个单位,括号内应“加上3”,即“左加右减”.
变式训练,深化提高
小结:
二次函数y=ax2与y=a(x-h)2的图象和性质
向上
向上
(h,0)
直线x=h
小结:
二次函数y=ax2与y=a(x-h)2的图象和性质
向上
向上
(h,0)
直线x=h
当xx > h 时, y随x的↑而↑.
当xx > h 时, y随x的↑而↓.
课堂小结
二次函数 y=a(x-h)2 的图象与 y=ax2 的图象的关系
左右平移规律:对解析式中自变量 “左加右减”
向右平移 个单位
向右平移 个单位
数学思想:
数形结合
分类思想
抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式,若 为该抛物线上两点,请比较 的大小.
解:二次函数y=ax2 的图象向右平移3个单位后的二次函数关系式可表示为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2, ,
∴平移后二次函数关系式为y= (x-3)2.
方法总结:根据抛物线左右平移的规律,向右平移3个单位后,a不变,括号内应“减去3”;若向左平移3个单位,括号内应“加上3”,即“左加右减”.
思考1:
思考2:
(1) 先向左平移2了单位,再向下平移3个
单位,得到的抛物线解析式为__________________.
(2) 经过怎样的平移变换能得到抛物线
?
22.1.3 二次函数 y=a(x-h) +k
的图象和性质(第2课时)
第二十二章 二次函数
二次函数 y=a(x-h) 的图象和性质
y=ax2+k
y=ax2
复习旧知,引入新课
a>0
a<0
上下平移
个单位
k>0
k<0
k<0
k>0
问题 函数 , 的图象,能否也可以由函数 平移得到?
复习旧知,引入新课
讲授新课
互动探究
例1.在如图所示的坐标系中,画出二次函数 ,
与 的图象.
解:先列表:
x ··· -4 -3 -2 -1 0 1 2 3 4 ···
··· ···
··· ···
··· ···
x ··· -4 -3 -2 -1 0 1 2 3 4 ···
··· ···
··· ···
··· ···
8
8
4.5
4.5
0.5
0.5
4.5
8
12.5
18
0.5
0.5
2
0
2
2
0
2
4.5
8
12.5
18
0.5
0.5
2
0
2
观察探究 得出新知
左加
右减
二次函数y=ax2与y=a(x-h)2的关系
一
平移规律: 对解析式中自变量 “左加右减”
开口方向 向上 向上 向上
顶点坐标 (-2,0) (0,0) (2,0)
对称轴 直线x=-2 直线x=0 直线x=2
最值 y最小值=0 y最小值=0 y最小值=0
增减性 当x <-2时,
y随x的↑而↓;
x >-2时,
y随x的↑而↑. 当x < 0时,
y随x的↑而↓;
x > 0时,
y随x的↑而↑. 当x < 2时,
y随x的↑而↓;
x > 2时,
y随x的↑而↑.
二次函数y=ax2与y=a(x-h)2的图象和性质
一
二次函数y=ax2与y=a(x-h)2的关系
一
例2.抛物线 , 与抛物线 有什么关系?
-2
2
-2
-4
-6
4
-4
想一想
左加
右减
巩固练习
(1)
(2)
(3)
(4)
(5)
向左平移5个单位
向右平移3个单位
?
?
向左平移2个单位
?
?
向右平移1个单位
练习1.请根据题意填空
向上平移2个单位
?
练习2:不画图象,直接说出下列抛物线的开口方向、顶点坐标及对称轴
(1)
(2)
向上,(3,0),直线x=3
向下,(﹣2,0),直线x=﹣2
练习3:
向右平移 个单位
向左平移 个单位
思考:二次函数 与 有什么关系?
练习4. 抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式.
解:二次函数y=ax2的图象向右平移3个单位后的二次函数关系式可表示为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2, ,
∴平移后二次函数关系式为y= (x-3)2.
方法总结:根据抛物线左右平移的规律,向右平移3个单位后,a不变,括号内应“减去3”;若向左平移3个单位,括号内应“加上3”,即“左加右减”.
变式训练,深化提高
小结:
二次函数y=ax2与y=a(x-h)2的图象和性质
向上
向上
(h,0)
直线x=h
小结:
二次函数y=ax2与y=a(x-h)2的图象和性质
向上
向上
(h,0)
直线x=h
当x
当x
课堂小结
二次函数 y=a(x-h)2 的图象与 y=ax2 的图象的关系
左右平移规律:对解析式中自变量 “左加右减”
向右平移 个单位
向右平移 个单位
数学思想:
数形结合
分类思想
抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式,若 为该抛物线上两点,请比较 的大小.
解:二次函数y=ax2 的图象向右平移3个单位后的二次函数关系式可表示为y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2, ,
∴平移后二次函数关系式为y= (x-3)2.
方法总结:根据抛物线左右平移的规律,向右平移3个单位后,a不变,括号内应“减去3”;若向左平移3个单位,括号内应“加上3”,即“左加右减”.
思考1:
思考2:
(1) 先向左平移2了单位,再向下平移3个
单位,得到的抛物线解析式为__________________.
(2) 经过怎样的平移变换能得到抛物线
?
同课章节目录
