苏科版八年级数学上册第一章《全等三角形》提优卷(Word版 含解析)
文档属性
| 名称 | 苏科版八年级数学上册第一章《全等三角形》提优卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 190.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 17:44:07 | ||
图片预览


文档简介
初二数学《全等三角形》提优卷
一
三角形全等证明中常见的辅助线
一、连线构造全等
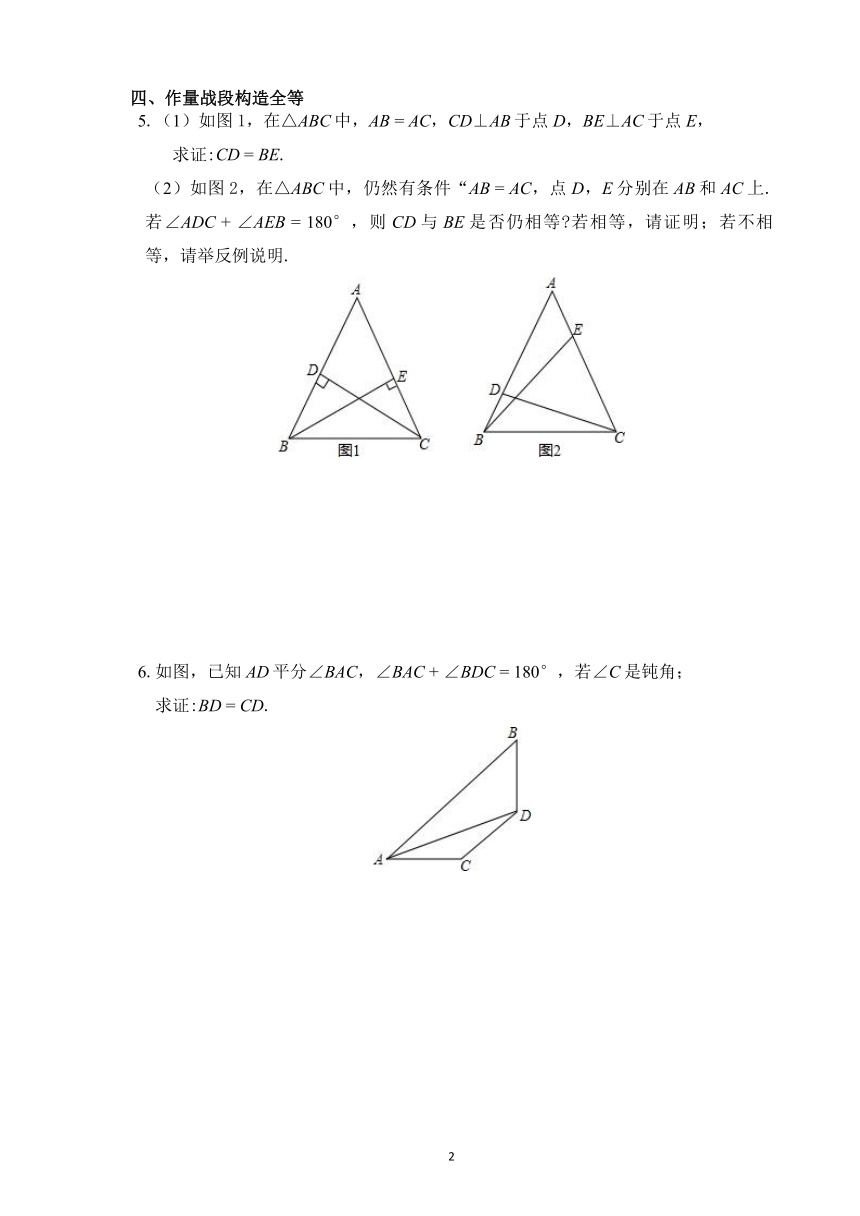
1.如图,在R△ABC中,∠A
=
90°,点D为斜边BC上一点,且BD
=
BA,过点D作BC的垂线交AC于点E.求证:点E在∠ABC的平分线上.
2.如图,AB
=
AE,∠C
=
∠D,BC
=
ED,点F是CD的中点,则AF平分∠BAE,试说明理由.
二、倍长中线构造全等
3.如图,在△ABC中,AD为BC边上的中线.求证:AB
+
AC
>
2AD.
三、做取构造全算
4.如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于点E,连接CE并延长交AP于点D.
求证:AD
+
BC
=
AB.
四、作量战段构造全等
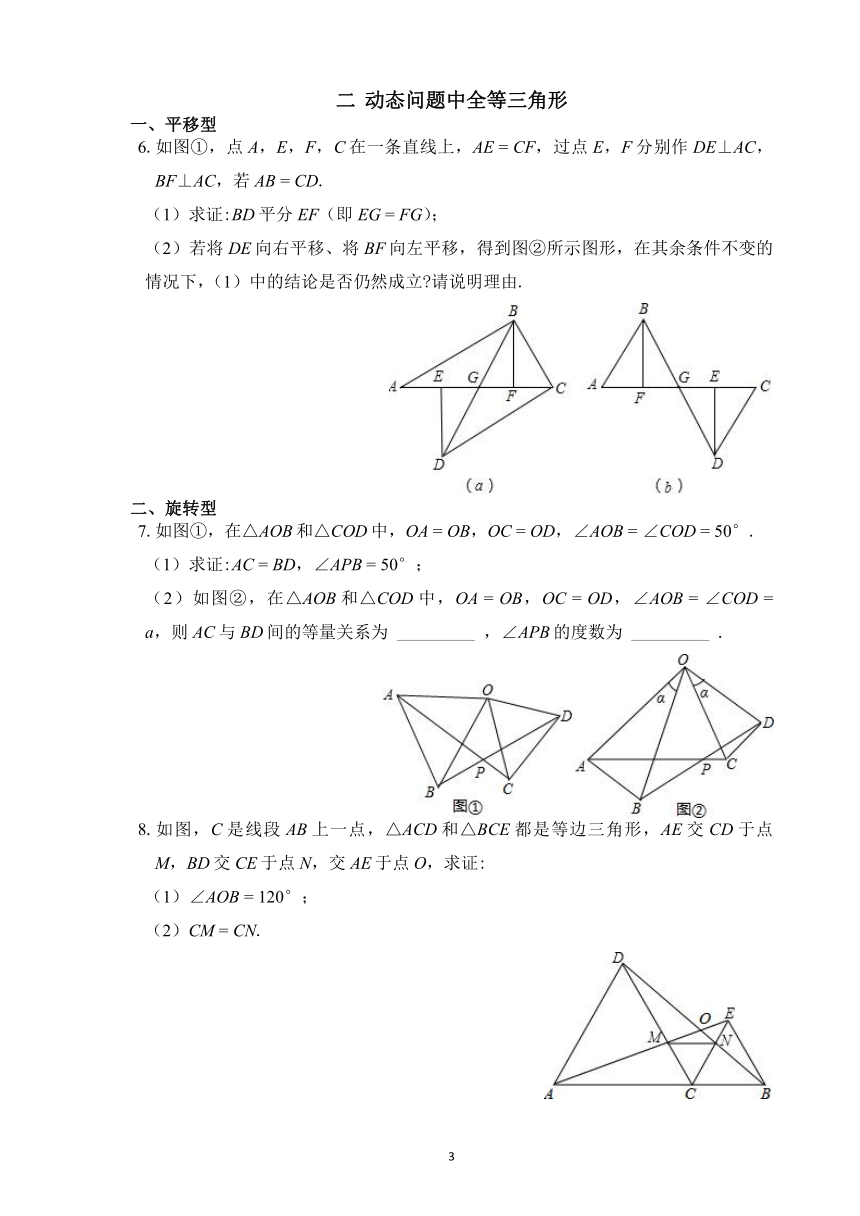
5.(1)如图1,在△ABC中,AB
=
AC,CD⊥AB于点D,BE⊥AC于点E,
求证:CD
=
BE.
(2)如图2,在△ABC中,仍然有条件“AB
=
AC,点D,E分别在AB和AC上.若∠ADC
+
∠AEB
=
180°,则CD与BE是否仍相等?若相等,请证明;若不相等,请举反例说明.
6.如图,已知AD平分∠BAC,∠BAC
+
∠BDC
=
180°,若∠C是钝角;
求证:BD
=
CD.
二
动态问题中全等三角形
一、平移型
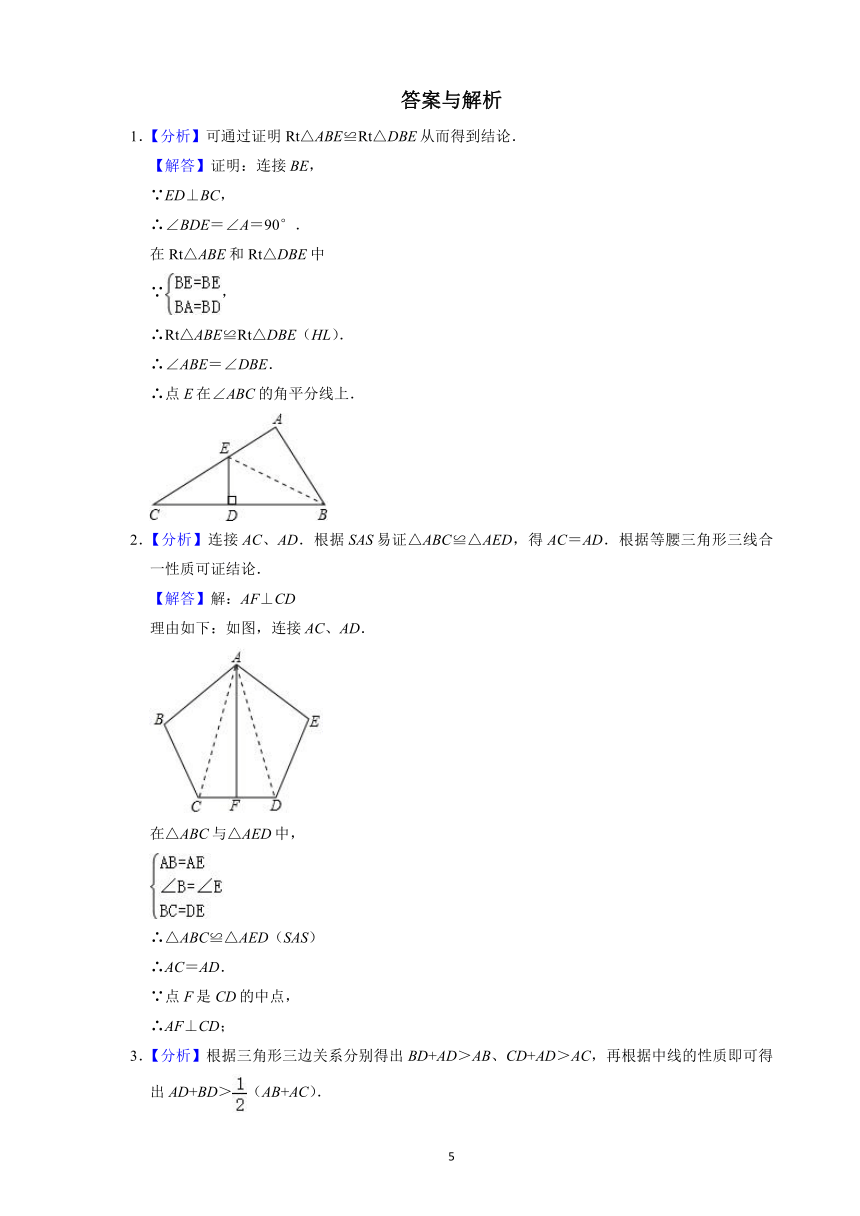
6.如图①,点A,E,F,C在一条直线上,AE
=
CF,过点E,F分别作DE⊥AC,BF⊥AC,若AB
=
CD.
(1)求证:BD平分EF(即EG
=
FG);
(2)若将DE向右平移、将BF向左平移,得到图②所示图形,在其余条件不变的情况下,(1)中的结论是否仍然成立?请说明理由.
二、旋转型
7.如图①,在△AOB和△COD中,OA
=
OB,OC
=
OD,∠AOB
=
∠COD
=
50°.
(1)求证:AC
=
BD,∠APB
=
50°;
(2)如图②,在△AOB和△COD中,OA
=
OB,OC
=
OD,∠AOB
=
∠COD
=
a,则AC与BD间的等量关系为
_________
,∠APB的度数为
_________
.
8.如图,C是线段AB上一点,△ACD和△BCE都是等边三角形,AE交CD于点M,BD交CE于点N,交AE于点O,求证:
(1)∠AOB
=
120°;
(2)CM
=
CN.
9.如图①,两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.
(1)在图①中,线段AC,BD的数量关系是
_________
;直线AC,BD相交成的角的度数是
_________
.
(2)将图①的△OAB绕点O顺时针旋转90°角,在图②中画出旋转后的△OAB.
(3)将图①中的△OAB绕点O顺时针旋转一个锐角,连接AC,BD得到图③,这时(1)中的两个结论是否成立?作出判断并说明理由.若△OAB绕点O继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.
三、动点问题
10.如图①,AB
=
4
cm,AC⊥AB,BD⊥AB,AC
=
BD
=
3
cm点P在线段AB上以1
cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t
=
1s时,△ACP与△BPQ是否全等?请说明理由,并判断此时线段PC和线段PQ的位置关系.
(2)如图②,将图①中的“AC⊥AB,BD⊥AB″改为”∠CAB
=
∠DBA
=
60°,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x,t的值;若不存在,请说明理由.
答案与解析
1.【分析】可通过证明Rt△ABE≌Rt△DBE从而得到结论.
【解答】证明:连接BE,
∵ED⊥BC,
∴∠BDE=∠A=90°.
在Rt△ABE和Rt△DBE中
∵,
∴Rt△ABE≌Rt△DBE(HL).
∴∠ABE=∠DBE.
∴点E在∠ABC的角平分线上.
2.【分析】连接AC、AD.根据SAS易证△ABC≌△AED,得AC=AD.根据等腰三角形三线合一性质可证结论.
【解答】解:AF⊥CD
理由如下:如图,连接AC、AD.
在△ABC与△AED中,
∴△ABC≌△AED(SAS)
∴AC=AD.
∵点F是CD的中点,
∴AF⊥CD;
3.【分析】根据三角形三边关系分别得出BD+AD>AB、CD+AD>AC,再根据中线的性质即可得出AD+BD>(AB+AC).
【解答】证明:∵BD+AD>AB,CD+AD>AC,
∴BD+AD+CD+AD>AB+AC.
∵AD是BC边上的中线,BD=CD,
∴AD+BD>(AB+AC).
4.【分析】首先在AB上截取AF=AD,由AE平分∠PAB,利用SAS即可证得△DAE≌△FAE,继而可证得∠EFB=∠C,然后利用AAS证得△BEF≌△BEC,即可得BC=BF,继而证得AD+BC=AB.
【解答】证明:在AB上截取AF=AD,
∵AE平分∠PAB,
∴∠DAE=∠FAE,
在△DAE和△FAE中,
∵,
∴△DAE≌△FAE(SAS),
∴∠AFE=∠ADE,
∵AD∥BC,
∴∠ADE+∠C=180°,
∵∠AFE+∠EFB=180°,
∴∠EFB=∠C,
∵BE平分∠ABC,
∴∠EBF=∠EBC,
在△BEF和△BEC中,
∵,
∴△BEF≌△BEC(AAS),
∴BC=BF,
∴AD+BC=AF+BF=AB.
5.(1)【分析】根据垂直的定义可得∠BDC=∠CEB=90°,根据等腰三角形的性质可得∠ABC=∠ACB,再有公共边BC,利用AAS可得△BCD≌△CBE,据此可得BD=CE.
【解答】证明:∵CD⊥AB,BE⊥AC,
∴∠BDC=∠CEB=90°,
∵AB=AC,
∴∠ABC=∠ACB,
在△BCD和△CBE中,
∠BDC=∠CEB,∠DBC=∠ECB,BC=CB,
∴△BCD≌△CBE(AAS),
∴BD=CE.
(2)【分析】分别作CF⊥AB,BG⊥AC,先证得△FBC≌△GCB,得出CF=BG,进而证得△CFD≌△BGE即可证得CD=BE.
【解答】解:CD=BE.
证明如下:如图2,分别作CF⊥AB,BG⊥AC,
∴∠CBF=90°,∠BGC=90°.
∵AB=AC,
∴∠ABC=∠ACB,
在△FBC和△GCB中,
,
∴△FBC≌△GCB(AAS).
∴CF=BG,
∵∠ADC+∠AEB=180°,
又∵∠BEG+∠AEB=180°,
∴∠ADC=∠BEG,
在△CFD和△BGE中,
,
∴△CFD≌△BGE(AAS),
∴CD=BE.
6.【分析】(1)根据四边形的内角和为360°,∠BAC+∠BDC=180°,可得∠B+∠C=180°,求出∠C的度数,利用等腰三角形的性质,求出∠DAC=∠ADC=25°,
根据AD平分∠BAC,所以∠BAC=2∠DAC=50°,得到∠BDC=130°,根据∠ADB=∠BDC﹣∠ADC,即可解答;
(2)过点D作DM⊥AB于M,DN⊥AC交AC延长线于N,证明△DMB≌△DNC,即可得出结论.
【解答】解:(1)∵∠BAC+∠BDC=180°,
∴∠B+∠C=180°,
∵∠B=50°,
∴∠C=130°,
∵∵AC=CD,∠C=130°,
∴∠DAC=∠ADC=(180°﹣∠C)÷2=25°,
∵AD平分∠BAC,
∴∠BAC=2∠DAC=50°,
∵∠BAC+∠BDC=180°,
∴∠BDC=130°,
∴∠ADB=∠BDC﹣∠ADC=130°﹣25°=105°.
(2)如图,过点D作DM⊥AB于M,DN⊥AC交AC延长线于N,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN,∠DMB=∠DNC=90,
∵∠ACD+∠B=180,∠ACD+∠DCN=180,
∴∠B=∠DCN,
在△BDM与△CDN中,
,
∴△DMB≌△DNC
(AAS),
∴BD=CD.
7.【分析】(1)△OAB绕点O顺时针旋转90°角应该在△COD的右边;
(2)的结论容易得到,AC=BD,AC与BD相交成90°的角;
(3)结论仍然成立,利用等腰直角三角形的性质可以得到全等条件证明△COA≌△DOB,然后利用全等三角形的性质可以证明结论仍然成立.
【解答】解:(1)如图(a)【A,B字母位置互换扣(1分),无弧扣(1分),不连接AB扣(1分),扣完为止)】(2分)
(2)AC=BD;90(90°)(每空1分)(4分)
(3)成立.如图(b).
∵∠COD=∠AOB=90°,
∴∠COA+∠AOD=∠AOD+∠DOB,
即:∠COA=∠DOB(或由旋转得∠COA=∠DOB),(5分)
∵CO=OD,OA=OB,
∴△COA≌△DOB,(6分)
∴AC=BD,(7分)
延长CA交OD于E,交BD于F,(下面的证法较多)
∵△COA≌△DOB,
∴∠ACO=∠ODB,(8分)
∵∠CEO=∠DEF,
∴∠COE=∠EFD=90°,
∴AC⊥BD.(9分)
旋转更大角时,结论仍然成立.(10分)
8.【分析】(1)根据等边三角形的性质得到AC=CD,CE=CB,∠ACD=∠BCE=60°,则可得到∠ACE=∠DCB,根据全等三角形的判定方法可得到△ACE≌△DCB,于是有∠CAM=∠CDN,由于∠ACD=DAC=∠BCE=∠CBE=60°,可得∠DCE=60°,则AD∥CE,DC∥BE,利用平行线的性质得到∠DAM=∠AEC,∠NDC=∠EBO,得出∠EBO=∠CAM,根据三角形的外角的性质即可求得;
(2)根据全等三角形的判定方法可得到△ACM≌△DCN,则CM=CN;
(3)根据等边三角形的判定方法即可得到△MCN为等边三角形,得出∠MNC=∠ECB=60°,根据内错角相等两直线平行得出MN∥AB.
【解答】证明:(1)∵△ACD和△BCE都是等边三角形,
∴AC=CD,CE=CB,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(SAS),
∴∠CAM=∠CDN,
∵∠ACD=DAC=∠BCE=∠CBE=60°,∠ACB是一个平角,
∴∠DCE=60°,
∴AD∥CE,DC∥BE,
∵AD∥CE,
∴∠DAM=∠AEC,
∵DC∥BE,
∴∠NDC=∠EBO,
∴∠EBO=∠CAM
∴∠AOB=∠OEB+∠EBO=∠AEC+∠CEB+∠EBO=∠DAE+∠CEB+∠CAM=∠DAC+∠CEB=60°+60°=120°;
(2)在△ACM和△DCN中,
,
∴△ACM≌△DCN(ASA),
∴CM=CN;
(3)∵CM=CN,∠DCE=60°,
∴△MCN为等边三角形,
∴∠MNC=60°,
∴∠MNC=∠ECB=60°,
∴MN∥AB.
9.【分析】(1)根据∠AOB=∠COD=50°求出∠AOC=∠BOD,根据SAS推出△AOC≌△BOD,根据全等三角形的性质得出AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,推出∠APB=∠AOB即可.
(2)根据∠AOB=∠COD=α求出∠AOC=∠BOD,根据SAS推出△AOC≌△BOD,根据全等三角形的性质得出AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,推出∠APB=∠AOB即可.
【解答】证明:(1)∵∠AOB=∠COD=50°,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,
∴∠APB=∠AOB=50°.
(2)解:AC=BD,∠APB=α,
理由是:∵∠AOB=∠COD=α,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,
∴∠APB=∠AOB=α,
故答案为:相等,α.
10.【分析】(1)利用SAS证得△ACP≌△BPQ,得出∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;
(2)由△ACP≌△BPQ,分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.
【解答】解:(1)当t=1时,AP=BQ=1,BP=AC=3,
又∵∠A=∠B=90°,
在△ACP和△BPQ中,
∴△ACP≌△BPQ(SAS).
∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,
即线段PC与线段PQ垂直.
(2)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
,
解得
;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
,
解得
;
综上所述,存在
或
使得△ACP与△BPQ全等.
【点评】本题主要考查了全等三角形的判定与性质,注意分类讨论思想的渗透.
1
一
三角形全等证明中常见的辅助线
一、连线构造全等
1.如图,在R△ABC中,∠A
=
90°,点D为斜边BC上一点,且BD
=
BA,过点D作BC的垂线交AC于点E.求证:点E在∠ABC的平分线上.
2.如图,AB
=
AE,∠C
=
∠D,BC
=
ED,点F是CD的中点,则AF平分∠BAE,试说明理由.
二、倍长中线构造全等
3.如图,在△ABC中,AD为BC边上的中线.求证:AB
+
AC
>
2AD.
三、做取构造全算
4.如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于点E,连接CE并延长交AP于点D.
求证:AD
+
BC
=
AB.
四、作量战段构造全等
5.(1)如图1,在△ABC中,AB
=
AC,CD⊥AB于点D,BE⊥AC于点E,
求证:CD
=
BE.
(2)如图2,在△ABC中,仍然有条件“AB
=
AC,点D,E分别在AB和AC上.若∠ADC
+
∠AEB
=
180°,则CD与BE是否仍相等?若相等,请证明;若不相等,请举反例说明.
6.如图,已知AD平分∠BAC,∠BAC
+
∠BDC
=
180°,若∠C是钝角;
求证:BD
=
CD.
二
动态问题中全等三角形
一、平移型
6.如图①,点A,E,F,C在一条直线上,AE
=
CF,过点E,F分别作DE⊥AC,BF⊥AC,若AB
=
CD.
(1)求证:BD平分EF(即EG
=
FG);
(2)若将DE向右平移、将BF向左平移,得到图②所示图形,在其余条件不变的情况下,(1)中的结论是否仍然成立?请说明理由.
二、旋转型
7.如图①,在△AOB和△COD中,OA
=
OB,OC
=
OD,∠AOB
=
∠COD
=
50°.
(1)求证:AC
=
BD,∠APB
=
50°;
(2)如图②,在△AOB和△COD中,OA
=
OB,OC
=
OD,∠AOB
=
∠COD
=
a,则AC与BD间的等量关系为
_________
,∠APB的度数为
_________
.
8.如图,C是线段AB上一点,△ACD和△BCE都是等边三角形,AE交CD于点M,BD交CE于点N,交AE于点O,求证:
(1)∠AOB
=
120°;
(2)CM
=
CN.
9.如图①,两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.
(1)在图①中,线段AC,BD的数量关系是
_________
;直线AC,BD相交成的角的度数是
_________
.
(2)将图①的△OAB绕点O顺时针旋转90°角,在图②中画出旋转后的△OAB.
(3)将图①中的△OAB绕点O顺时针旋转一个锐角,连接AC,BD得到图③,这时(1)中的两个结论是否成立?作出判断并说明理由.若△OAB绕点O继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.
三、动点问题
10.如图①,AB
=
4
cm,AC⊥AB,BD⊥AB,AC
=
BD
=
3
cm点P在线段AB上以1
cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t
=
1s时,△ACP与△BPQ是否全等?请说明理由,并判断此时线段PC和线段PQ的位置关系.
(2)如图②,将图①中的“AC⊥AB,BD⊥AB″改为”∠CAB
=
∠DBA
=
60°,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x,t的值;若不存在,请说明理由.
答案与解析
1.【分析】可通过证明Rt△ABE≌Rt△DBE从而得到结论.
【解答】证明:连接BE,
∵ED⊥BC,
∴∠BDE=∠A=90°.
在Rt△ABE和Rt△DBE中
∵,
∴Rt△ABE≌Rt△DBE(HL).
∴∠ABE=∠DBE.
∴点E在∠ABC的角平分线上.
2.【分析】连接AC、AD.根据SAS易证△ABC≌△AED,得AC=AD.根据等腰三角形三线合一性质可证结论.
【解答】解:AF⊥CD
理由如下:如图,连接AC、AD.
在△ABC与△AED中,
∴△ABC≌△AED(SAS)
∴AC=AD.
∵点F是CD的中点,
∴AF⊥CD;
3.【分析】根据三角形三边关系分别得出BD+AD>AB、CD+AD>AC,再根据中线的性质即可得出AD+BD>(AB+AC).
【解答】证明:∵BD+AD>AB,CD+AD>AC,
∴BD+AD+CD+AD>AB+AC.
∵AD是BC边上的中线,BD=CD,
∴AD+BD>(AB+AC).
4.【分析】首先在AB上截取AF=AD,由AE平分∠PAB,利用SAS即可证得△DAE≌△FAE,继而可证得∠EFB=∠C,然后利用AAS证得△BEF≌△BEC,即可得BC=BF,继而证得AD+BC=AB.
【解答】证明:在AB上截取AF=AD,
∵AE平分∠PAB,
∴∠DAE=∠FAE,
在△DAE和△FAE中,
∵,
∴△DAE≌△FAE(SAS),
∴∠AFE=∠ADE,
∵AD∥BC,
∴∠ADE+∠C=180°,
∵∠AFE+∠EFB=180°,
∴∠EFB=∠C,
∵BE平分∠ABC,
∴∠EBF=∠EBC,
在△BEF和△BEC中,
∵,
∴△BEF≌△BEC(AAS),
∴BC=BF,
∴AD+BC=AF+BF=AB.
5.(1)【分析】根据垂直的定义可得∠BDC=∠CEB=90°,根据等腰三角形的性质可得∠ABC=∠ACB,再有公共边BC,利用AAS可得△BCD≌△CBE,据此可得BD=CE.
【解答】证明:∵CD⊥AB,BE⊥AC,
∴∠BDC=∠CEB=90°,
∵AB=AC,
∴∠ABC=∠ACB,
在△BCD和△CBE中,
∠BDC=∠CEB,∠DBC=∠ECB,BC=CB,
∴△BCD≌△CBE(AAS),
∴BD=CE.
(2)【分析】分别作CF⊥AB,BG⊥AC,先证得△FBC≌△GCB,得出CF=BG,进而证得△CFD≌△BGE即可证得CD=BE.
【解答】解:CD=BE.
证明如下:如图2,分别作CF⊥AB,BG⊥AC,
∴∠CBF=90°,∠BGC=90°.
∵AB=AC,
∴∠ABC=∠ACB,
在△FBC和△GCB中,
,
∴△FBC≌△GCB(AAS).
∴CF=BG,
∵∠ADC+∠AEB=180°,
又∵∠BEG+∠AEB=180°,
∴∠ADC=∠BEG,
在△CFD和△BGE中,
,
∴△CFD≌△BGE(AAS),
∴CD=BE.
6.【分析】(1)根据四边形的内角和为360°,∠BAC+∠BDC=180°,可得∠B+∠C=180°,求出∠C的度数,利用等腰三角形的性质,求出∠DAC=∠ADC=25°,
根据AD平分∠BAC,所以∠BAC=2∠DAC=50°,得到∠BDC=130°,根据∠ADB=∠BDC﹣∠ADC,即可解答;
(2)过点D作DM⊥AB于M,DN⊥AC交AC延长线于N,证明△DMB≌△DNC,即可得出结论.
【解答】解:(1)∵∠BAC+∠BDC=180°,
∴∠B+∠C=180°,
∵∠B=50°,
∴∠C=130°,
∵∵AC=CD,∠C=130°,
∴∠DAC=∠ADC=(180°﹣∠C)÷2=25°,
∵AD平分∠BAC,
∴∠BAC=2∠DAC=50°,
∵∠BAC+∠BDC=180°,
∴∠BDC=130°,
∴∠ADB=∠BDC﹣∠ADC=130°﹣25°=105°.
(2)如图,过点D作DM⊥AB于M,DN⊥AC交AC延长线于N,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN,∠DMB=∠DNC=90,
∵∠ACD+∠B=180,∠ACD+∠DCN=180,
∴∠B=∠DCN,
在△BDM与△CDN中,
,
∴△DMB≌△DNC
(AAS),
∴BD=CD.
7.【分析】(1)△OAB绕点O顺时针旋转90°角应该在△COD的右边;
(2)的结论容易得到,AC=BD,AC与BD相交成90°的角;
(3)结论仍然成立,利用等腰直角三角形的性质可以得到全等条件证明△COA≌△DOB,然后利用全等三角形的性质可以证明结论仍然成立.
【解答】解:(1)如图(a)【A,B字母位置互换扣(1分),无弧扣(1分),不连接AB扣(1分),扣完为止)】(2分)
(2)AC=BD;90(90°)(每空1分)(4分)
(3)成立.如图(b).
∵∠COD=∠AOB=90°,
∴∠COA+∠AOD=∠AOD+∠DOB,
即:∠COA=∠DOB(或由旋转得∠COA=∠DOB),(5分)
∵CO=OD,OA=OB,
∴△COA≌△DOB,(6分)
∴AC=BD,(7分)
延长CA交OD于E,交BD于F,(下面的证法较多)
∵△COA≌△DOB,
∴∠ACO=∠ODB,(8分)
∵∠CEO=∠DEF,
∴∠COE=∠EFD=90°,
∴AC⊥BD.(9分)
旋转更大角时,结论仍然成立.(10分)
8.【分析】(1)根据等边三角形的性质得到AC=CD,CE=CB,∠ACD=∠BCE=60°,则可得到∠ACE=∠DCB,根据全等三角形的判定方法可得到△ACE≌△DCB,于是有∠CAM=∠CDN,由于∠ACD=DAC=∠BCE=∠CBE=60°,可得∠DCE=60°,则AD∥CE,DC∥BE,利用平行线的性质得到∠DAM=∠AEC,∠NDC=∠EBO,得出∠EBO=∠CAM,根据三角形的外角的性质即可求得;
(2)根据全等三角形的判定方法可得到△ACM≌△DCN,则CM=CN;
(3)根据等边三角形的判定方法即可得到△MCN为等边三角形,得出∠MNC=∠ECB=60°,根据内错角相等两直线平行得出MN∥AB.
【解答】证明:(1)∵△ACD和△BCE都是等边三角形,
∴AC=CD,CE=CB,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠DCB,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(SAS),
∴∠CAM=∠CDN,
∵∠ACD=DAC=∠BCE=∠CBE=60°,∠ACB是一个平角,
∴∠DCE=60°,
∴AD∥CE,DC∥BE,
∵AD∥CE,
∴∠DAM=∠AEC,
∵DC∥BE,
∴∠NDC=∠EBO,
∴∠EBO=∠CAM
∴∠AOB=∠OEB+∠EBO=∠AEC+∠CEB+∠EBO=∠DAE+∠CEB+∠CAM=∠DAC+∠CEB=60°+60°=120°;
(2)在△ACM和△DCN中,
,
∴△ACM≌△DCN(ASA),
∴CM=CN;
(3)∵CM=CN,∠DCE=60°,
∴△MCN为等边三角形,
∴∠MNC=60°,
∴∠MNC=∠ECB=60°,
∴MN∥AB.
9.【分析】(1)根据∠AOB=∠COD=50°求出∠AOC=∠BOD,根据SAS推出△AOC≌△BOD,根据全等三角形的性质得出AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,推出∠APB=∠AOB即可.
(2)根据∠AOB=∠COD=α求出∠AOC=∠BOD,根据SAS推出△AOC≌△BOD,根据全等三角形的性质得出AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,推出∠APB=∠AOB即可.
【解答】证明:(1)∵∠AOB=∠COD=50°,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,
∴∠APB=∠AOB=50°.
(2)解:AC=BD,∠APB=α,
理由是:∵∠AOB=∠COD=α,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,
∴∠APB=∠AOB=α,
故答案为:相等,α.
10.【分析】(1)利用SAS证得△ACP≌△BPQ,得出∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;
(2)由△ACP≌△BPQ,分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.
【解答】解:(1)当t=1时,AP=BQ=1,BP=AC=3,
又∵∠A=∠B=90°,
在△ACP和△BPQ中,
∴△ACP≌△BPQ(SAS).
∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,
即线段PC与线段PQ垂直.
(2)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
,
解得
;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
,
解得
;
综上所述,存在
或
使得△ACP与△BPQ全等.
【点评】本题主要考查了全等三角形的判定与性质,注意分类讨论思想的渗透.
1
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
