苏科版七年级数学上册 第2章 有理数培优提高学案(Word版 无答案)
文档属性
| 名称 | 苏科版七年级数学上册 第2章 有理数培优提高学案(Word版 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 327.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览




文档简介
有理数培优提高
Eg1:【概念新定义】:
a是不为2的有理数,我们把称为a的“哈利数”,如3的“哈利数”是=﹣2,﹣2的“哈利数”是=,已知a1=5,a2是a1的“哈利数”,a3是a2的“哈利数”,a4是a3的“哈利数”,…,依此类推,则a2020等于( )
A.
B.
C.
D.5
【跟踪练习1】:定义:是不为1的有理数,我们把称为的差倒数,如:2的差倒数是,的差倒数是.已知,是的差倒数,是的差倒数,……,依此
=
.
A.
B.
C.4
D.
Eg2:【运算新定义】:
1.在实数的原有运算法则中,我们补充定义新运算“?”如下:当a≥b时,a?b=b2;当a<b时,a?b=a.则当x=2时,(1?x)?x﹣(3?x)的值为 _________ .(“?”和“﹣”仍为实数运算中的乘号和减号)
【跟踪练习1】:叫做二阶行列式,它的算法是:ad﹣bc,请你计算= _________ .
【跟踪练习2】:正整数1到n的连乘积,用n!表示,这是我们还没学过的新运算(高中称为阶乘),这种运算规定:1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…,n!=n×(n﹣1)×(n﹣2)×…×3×2×1.在这种规定下,请你计算= _________ .
【跟踪练习3】:定义新运算“?”,a?b=a-4b,则12?(-1)=__________。
2.计算机中常用的十六进制是逢16进l的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
例如,用十六进制表示C+F=1B.19-F=A,18÷4=6,则A×B=
(
)
A.72.
B.6E
.
C.5F
.
D.B0.
【跟踪练习】:定义一种运算:k是正整数,且k≥2,[x]表示非负实数x的整数部分,例如[1.6]=1,[0.3]=0.若a1=1,则a2020= _________ .
Eg3:【周期性规律问题】:
【例】:观察下列算式:
31=3
32=9
33=27
34=81
35=243
36=729
37=2187
……
根据上述算式中的规律,你认为32020的末位数字是
【跟踪练习1】:将正整数按如图所示的位詈顺序排列:根据排列规律,则2020应在(
)
A位置
B位置
C位置
D位置
【跟踪练习2】:如图,平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF,从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…,则数字“2008”在( )
A.射线OA上
B.射线OB
上
C.射线OD上
D.射线OF
上
【跟踪练习3】:将正整数1,2,3,4……按以下方式排列
1
4
→
5
8
→
9
12
→
……
↓
↑
↓
↑
↓
↑
2
→
3
6
→
7
10
→
11
根据排例规律,从2019到2020的箭头依次为
A.↓
→
B.→
↓
C.↑
→
D.
→
↑
【跟踪练习4】:如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第20次“移位”后,则他所处顶点的编号为
.
【跟踪练习5】:.等边三角形纸板ABC
在数轴上的位置如图所示,点A、B对应的数分别为0和﹣1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转第1次后,点C所对应的数为1,则翻转2014次后,点C所对应的数是( )
A.2011
B.2012
C.2013
D.2014
【跟踪练习6】:如下图所示?,?在?1000?个“〇”中依次填入一列数字?,,,…,?使得其中任意四个相邻“〇”中所填数字之和都等于?10,已知=5,
则=__
_.
Eg4:【其他类规律问题】:
【例1】:一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分如图,
则这串珠子被盒子遮住的部分有
颗.
【跟踪练习】:填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )A.
38
B.
52
C.
66
D.
74
【例2】:.将从1开始的连续自然数按以下规律排列:
第1行
1
第2行
2
3
4
第3行
9
8
7
6
5
第4行
10
11
12
13
14
15
16
第5行
25
24
23
22
21
20
19
18
17
…则2020在第
行第
个(从左往右数)
【跟踪练习1】:正整数按如图的规律排列,请写出第20行,第20列的数字
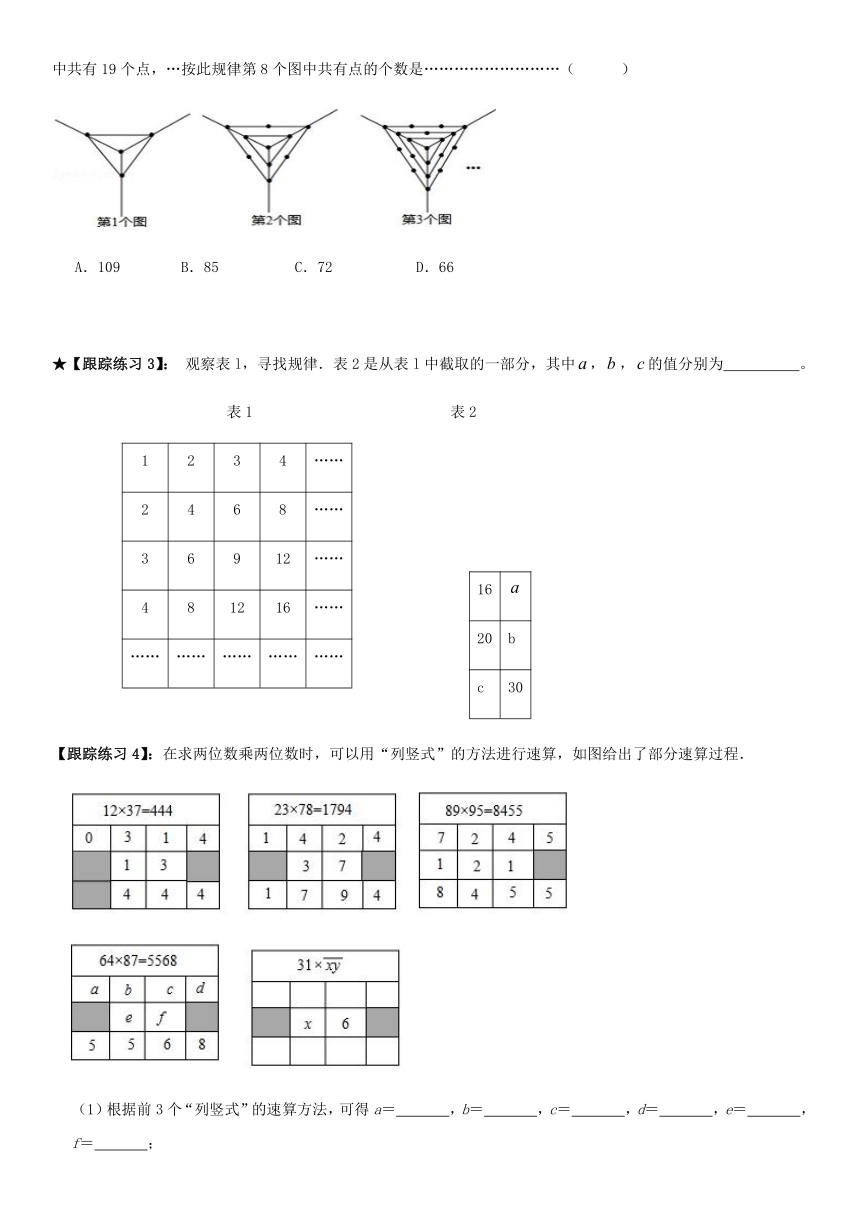
【跟踪练习2】:.观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第8个图中共有点的个数是………………………(
)
A.109
B.85
C.72
D.66
★【跟踪练习3】:
观察表l,寻找规律.表2是从表l中截取的一部分,其中,,的值分别为
。
表1
表2
1
2
3
4
……
2
4
6
8
……
3
6
9
12
……
4
8
12
16
……
……
……
……
……
……
16
20
b
c
30
【跟踪练习4】:在求两位数乘两位数时,可以用“列竖式”的方法进行速算,如图给出了部分速算过程.
(1)根据前3个“列竖式”的速算方法,可得a=
,b=
,c=
,d=
,e=
,f=
;
(2)根据前3个“列竖式”的速算方法,在速算“31×”时,给出了部分过程如图所示.则这个两位数可能为
.
【例3】:德国数学家洛萨提出了一个猜想:如果n为奇数
,我们计算3n+1;如果n为偶数,我们除以2,不断重复这样的运算,经过有限步骤后一定可以得到1.例如,n=5时,经过上述运算,依次得到一列数5,16,8,4,2,1.(
注:计算到1结束),若n=12,得到一列数的和为
;若小明同学对某个整数n,按照上述运算,得到一列数,已知第八个数为1,则整数n的所有可能取值中,最小的值为
.
【跟踪练习】:.有依次排列的3个数:6,2,8,对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:6,-4,2,6,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:6,-10,-4,6,2,4,6,2,8,继续依次操作下去,则从数串6,2,8开始操作第2
015次以后所产生的新数串的所有数之和是
.
【例4】:一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动,设该机器人每秒钟前进或后退1步,并且每步的距离为1个单位长,xn表示第n秒时机器人在数轴上的位置所对应的数,给出下列结论(1)x3=3,(2)x5=1,(3)x76>x77,(4)x103<x104,(5)x2018>x2019其中,正确结论的个数是( )
A.
1个
B.
2个
C.
3个
D.
4个
【跟踪练习】:如图,在数轴上,A1、P两点表示的数分别为1、2,A1、A2关于O对称,A2、A3关于点P对称,A3、A4关于点O对称,A4、A5关于点P对称…依次规律,则点A15表示的数是 .
Eg5:【流程图类找规律】:
在图示的运算流程中,若输出的数y=5,则输入的数x=
.
【跟踪练习1】:如图是一个简单的数值运算程序,当输入的值为3时,则输出的结果为
.
【跟踪练习2】:如图是一个“数字转换器”(箭头是指数进入转换器的路径,方框是对进入的数进行转换的转换器)
(1)当小明分别输入3,时,输出的结果分别是:
,
.
(2)当输入的数字为
时(写出两个即可),其输出结果是0
.
(3)你认为这个“数字转换器”不可能输出的数是:
.
★【跟踪练习3】:.如图,是一个计算装置示意图,J1、J2是数据输入口,C是计算输出口,计算过程是由J1、J2分别输入自然数m和n,经计算后得自然数K由C输出,此种计算装置完成的计算满足以下三个性质:
(1)若J1、J=2分别输入1,则输出结果为1;
(2)若J=1输入任何固定的自然数不变,J2输入自然数增大1,则输出结果比原来增大2;
(3)若J2输入1,J1输入自然数增大1,则输出结果为原来的2倍.
试问:(1)若J1输入1,J2输入自然数n,输出结果为多少?
(2)若J2输入1,J1输入自然数m,输出结果为多少?
(3)若J1输入自然数m,J2输入自然数n,输出的结果为多少?17.计算:
Eg6:【实际问题】:
【例1】:一只蚂蚁从地面开始爬树,它每天不停地往上爬,不幸的是,它每天白天能往上爬3米,可是一到夜里就要滑下2米,但是蚂蚁还是坚持往上爬,这棵树高是20米,蚂蚁从清晨开始从地面往上爬,它需要几天才能爬到树的最高处?( )
A.
17天
B.
18天
C.
19天
D.
20天
【跟踪练习】:一只蚂蚁从地面开始爬树,它每天不停地往上爬,不幸的是,它每天白天能往上爬5米,可是一到夜里就要滑下3米,但是蚂蚁还是坚持往上爬,这棵树高是50米,蚂蚁从清晨开始从地面往上爬,它需要
天才能爬到树的最高处
【例2】:不法商贩使用“八两称”坑害消费者,用这种称称东西,小吴以2.0元/kg的价格从不法商贩处买了8kg香蕉,那么他被商贩坑了 _________ 元钱.
【跟踪练习1】:“六?一”儿童节期间,某商场为吸引顾客,实行“买100送20,连环送”的活动,即顾客购物满100元,就可以获赠商场购物券20元,不足100元的部分不赠券,并且购物可以用现金,也可以用购物券.如果你有340元现金,在活动期间到该商场购物,最多可以获赠购物券累计为 _________ 元.
★【跟踪练习2】:老财主临终前将全部银元分给他的四个儿子.老大分得全部银元4等份中的1份,多出的1枚银元给了丫环;老二分得余下银元4等份中的1份,多出的1枚银元给了丫环;老三分得余下银元4等份中的1份,多出的1枚银元给了丫环;老四分得余下银元4等份中的1份,多出的1枚银元给了丫环;余下的银元又分成4等份,四个儿子各得一份,多出的1枚银元给了丫环.问老财主至少要有多少块银元才够分.
【跟踪练习3】:.股民小杨上星期五买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况(单位:元):
星期
一
二
三
四
五
每股涨跌
+220
+142
-080
-252
+130
(1)星期三收盘时,该股票涨或跌了多少元?
(2)本周内该股票的最高价是每股多少元?最底价是每股多少元?
(3)已知小杨了15‰的手续费,卖出时还需要付成交额的15‰的手续费和1‰的交易税如果小杨在星期五收盘前将全部股票卖出,则他的收益情况如何?
【跟踪练习4】:小明的妈妈在某玩具厂工作,厂里规定每个工人每周要生产某种玩具210个,平均每天生产30个,但由于种种原因,实际每天生产量与计划量相比有出入.下表是小明妈妈某周的生产情况(超产记为正、减产记为负):
(1)根据记录的数据可知小明妈妈星期三生产玩具__________个;
(2)根据记录的数据可知小明妈妈本周实际生产玩具__________个;
(3)该厂实行“每日计件工资制”。每生产一个玩具可得工资5元,若超额完成任务,则超过部分每个另奖3元;少生产一个则倒扣2元,那么小明妈妈这一周的工资总额是多少元?
(4)若将上面第(3)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,在此方式下小明妈妈这一周的工资与按日计件的工资哪一个更多?请说明理由.
Eg7:【类比推理类问题】:
【例】:为了求的值,可令,则
,因此,,所以.
即.
仿照以上的过程,计算:
=
.
【跟踪练习1】:阅读下面一段:计算1+5+52+53…+599+5100
观察发现,上式从第二项起,每项都是它前面一项的5倍,如果将上式各项都乘以5,所得新算式中除个别项外,其余与原式中的项相同,于是两式相减将使差易于计算.
解:设S=1+5+52+53…+599+5100,①
则5S=5+52+…+5100+5101,②
由②﹣①得4S=5101﹣1,则S=.
上面计算用的方法称为“错位相减法”,如果一列数,从第二项起每一项与前一项之比都相等(本例中是都等于5),那么这列数的求和问题,均可用上述“错位相减”法来解决.
下面请你观察算式1++++…+是否具备上述规律?若是,请你尝试用“错位相减”法计算上式的结果.
【跟踪练习2】:观察下列等式:,,,将以上三个等式两边分别相加得:
(1)猜想并写出:= _________ ;
(2)直接写出下列各式的计算结果:
①= _________ ;
②= _________ .
(3)探究并计算:.
Eg8:【阅读理解类问题】:
【例】:在解决数学问题的过程中,我们常用到
“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.
【提出问题】三个有理数满足,求的值.
【解决问题】[来m]
解:由题意,得三个有理数都为正数或其中一个为正数,另两个为负数.
①都是正数,即时,则;
②当中有一个为正数,另两个为负数时,不妨设,则
.
综上所述,值为3或-1.
【探究】请根据上面的解题思路解答下面的问题:
(1)三个有理数满足,求的值;
(2)若为三个不为0的有理数,且,求的值.
【跟踪练习1】:我们知道,表示数对应的点到原点的距离,这是绝对值的几何意义.进一步地,数轴上两个点分别表示数,那么.利用此结论,回答下列问题:
数轴上表示2和5的两点之间的距离是,数轴上表示-2和-5的两点之间的距离是
,
数轴上表示1和-3的两点之间的距离是
;
(2)数轴上表示和-1的两点之间的距离是
,如果=2,那么的值为
;[来
(3)写出表示的几何意义:
,该式的最小值为
;
(4)求的最小值.
.
【跟踪练习2】:阅读:已知点
A、B
在数轴上分别表示有理数、,A、B
两点之间的距离
表示为|AB|=||.
理解:
(1)数轴上表示
2和3的两点之间的距离是;
(2)数轴上表示
x
和5的两点
A
和
B
之间的距离是;
(3)代数式|x3|+|x+5|最小值是.
应用:如图,一条公路经过某个科技园区,该园区内有三家公司A、B、C分别位于公路的两侧,现要在园区内建一个公交站点H,已知AB=2000m,BC=3000m,问公交站点H建在图中何处,才能使得站点H到四个公司路程之和最短?最短路程是多少?请你仿照上面列式计算。
k.Com]
Eg9:【其他类问题】:
【例】:如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,若没有左右移动则记为0;第二个数表示上下方向,若没有上下移动则记为0.那么图中(9分)
(1)A→D(
,
),C→B(
,
),D→
(-3,+2);
(2)若贝贝的行走路线为A→B→D→C,请计算贝贝走过的路程;
(
3)若贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(+2,-1),(-1,+3),
(-2,-1),请在上图中标出妮妮的位置E点.
(4)在(3)中贝贝若每走1m需消耗2.5焦耳的能量,
则贝贝寻找妮妮过程中共需消耗多少焦耳的能量?
【跟踪练习1】:为确保信息安全,信息需加密传输,发送方由明文?密文(加密),接收方由密文?明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d.例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为 _________ .
【跟踪练习2】:已知两数、互为相反数,、互为倒数,的绝对值是2,
求的值。
【跟踪练习3】:若|x|=2,y2=9,且x>0,y<0,则x+y= _________ .
Eg1:【概念新定义】:
a是不为2的有理数,我们把称为a的“哈利数”,如3的“哈利数”是=﹣2,﹣2的“哈利数”是=,已知a1=5,a2是a1的“哈利数”,a3是a2的“哈利数”,a4是a3的“哈利数”,…,依此类推,则a2020等于( )
A.
B.
C.
D.5
【跟踪练习1】:定义:是不为1的有理数,我们把称为的差倒数,如:2的差倒数是,的差倒数是.已知,是的差倒数,是的差倒数,……,依此
=
.
A.
B.
C.4
D.
Eg2:【运算新定义】:
1.在实数的原有运算法则中,我们补充定义新运算“?”如下:当a≥b时,a?b=b2;当a<b时,a?b=a.则当x=2时,(1?x)?x﹣(3?x)的值为 _________ .(“?”和“﹣”仍为实数运算中的乘号和减号)
【跟踪练习1】:叫做二阶行列式,它的算法是:ad﹣bc,请你计算= _________ .
【跟踪练习2】:正整数1到n的连乘积,用n!表示,这是我们还没学过的新运算(高中称为阶乘),这种运算规定:1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…,n!=n×(n﹣1)×(n﹣2)×…×3×2×1.在这种规定下,请你计算= _________ .
【跟踪练习3】:定义新运算“?”,a?b=a-4b,则12?(-1)=__________。
2.计算机中常用的十六进制是逢16进l的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
例如,用十六进制表示C+F=1B.19-F=A,18÷4=6,则A×B=
(
)
A.72.
B.6E
.
C.5F
.
D.B0.
【跟踪练习】:定义一种运算:k是正整数,且k≥2,[x]表示非负实数x的整数部分,例如[1.6]=1,[0.3]=0.若a1=1,则a2020= _________ .
Eg3:【周期性规律问题】:
【例】:观察下列算式:
31=3
32=9
33=27
34=81
35=243
36=729
37=2187
……
根据上述算式中的规律,你认为32020的末位数字是
【跟踪练习1】:将正整数按如图所示的位詈顺序排列:根据排列规律,则2020应在(
)
A位置
B位置
C位置
D位置
【跟踪练习2】:如图,平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF,从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…,则数字“2008”在( )
A.射线OA上
B.射线OB
上
C.射线OD上
D.射线OF
上
【跟踪练习3】:将正整数1,2,3,4……按以下方式排列
1
4
→
5
8
→
9
12
→
……
↓
↑
↓
↑
↓
↑
2
→
3
6
→
7
10
→
11
根据排例规律,从2019到2020的箭头依次为
A.↓
→
B.→
↓
C.↑
→
D.
→
↑
【跟踪练习4】:如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第20次“移位”后,则他所处顶点的编号为
.
【跟踪练习5】:.等边三角形纸板ABC
在数轴上的位置如图所示,点A、B对应的数分别为0和﹣1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转第1次后,点C所对应的数为1,则翻转2014次后,点C所对应的数是( )
A.2011
B.2012
C.2013
D.2014
【跟踪练习6】:如下图所示?,?在?1000?个“〇”中依次填入一列数字?,,,…,?使得其中任意四个相邻“〇”中所填数字之和都等于?10,已知=5,
则=__
_.
Eg4:【其他类规律问题】:
【例1】:一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分如图,
则这串珠子被盒子遮住的部分有
颗.
【跟踪练习】:填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )A.
38
B.
52
C.
66
D.
74
【例2】:.将从1开始的连续自然数按以下规律排列:
第1行
1
第2行
2
3
4
第3行
9
8
7
6
5
第4行
10
11
12
13
14
15
16
第5行
25
24
23
22
21
20
19
18
17
…则2020在第
行第
个(从左往右数)
【跟踪练习1】:正整数按如图的规律排列,请写出第20行,第20列的数字
【跟踪练习2】:.观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第8个图中共有点的个数是………………………(
)
A.109
B.85
C.72
D.66
★【跟踪练习3】:
观察表l,寻找规律.表2是从表l中截取的一部分,其中,,的值分别为
。
表1
表2
1
2
3
4
……
2
4
6
8
……
3
6
9
12
……
4
8
12
16
……
……
……
……
……
……
16
20
b
c
30
【跟踪练习4】:在求两位数乘两位数时,可以用“列竖式”的方法进行速算,如图给出了部分速算过程.
(1)根据前3个“列竖式”的速算方法,可得a=
,b=
,c=
,d=
,e=
,f=
;
(2)根据前3个“列竖式”的速算方法,在速算“31×”时,给出了部分过程如图所示.则这个两位数可能为
.
【例3】:德国数学家洛萨提出了一个猜想:如果n为奇数
,我们计算3n+1;如果n为偶数,我们除以2,不断重复这样的运算,经过有限步骤后一定可以得到1.例如,n=5时,经过上述运算,依次得到一列数5,16,8,4,2,1.(
注:计算到1结束),若n=12,得到一列数的和为
;若小明同学对某个整数n,按照上述运算,得到一列数,已知第八个数为1,则整数n的所有可能取值中,最小的值为
.
【跟踪练习】:.有依次排列的3个数:6,2,8,对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:6,-4,2,6,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:6,-10,-4,6,2,4,6,2,8,继续依次操作下去,则从数串6,2,8开始操作第2
015次以后所产生的新数串的所有数之和是
.
【例4】:一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动,设该机器人每秒钟前进或后退1步,并且每步的距离为1个单位长,xn表示第n秒时机器人在数轴上的位置所对应的数,给出下列结论(1)x3=3,(2)x5=1,(3)x76>x77,(4)x103<x104,(5)x2018>x2019其中,正确结论的个数是( )
A.
1个
B.
2个
C.
3个
D.
4个
【跟踪练习】:如图,在数轴上,A1、P两点表示的数分别为1、2,A1、A2关于O对称,A2、A3关于点P对称,A3、A4关于点O对称,A4、A5关于点P对称…依次规律,则点A15表示的数是 .
Eg5:【流程图类找规律】:
在图示的运算流程中,若输出的数y=5,则输入的数x=
.
【跟踪练习1】:如图是一个简单的数值运算程序,当输入的值为3时,则输出的结果为
.
【跟踪练习2】:如图是一个“数字转换器”(箭头是指数进入转换器的路径,方框是对进入的数进行转换的转换器)
(1)当小明分别输入3,时,输出的结果分别是:
,
.
(2)当输入的数字为
时(写出两个即可),其输出结果是0
.
(3)你认为这个“数字转换器”不可能输出的数是:
.
★【跟踪练习3】:.如图,是一个计算装置示意图,J1、J2是数据输入口,C是计算输出口,计算过程是由J1、J2分别输入自然数m和n,经计算后得自然数K由C输出,此种计算装置完成的计算满足以下三个性质:
(1)若J1、J=2分别输入1,则输出结果为1;
(2)若J=1输入任何固定的自然数不变,J2输入自然数增大1,则输出结果比原来增大2;
(3)若J2输入1,J1输入自然数增大1,则输出结果为原来的2倍.
试问:(1)若J1输入1,J2输入自然数n,输出结果为多少?
(2)若J2输入1,J1输入自然数m,输出结果为多少?
(3)若J1输入自然数m,J2输入自然数n,输出的结果为多少?17.计算:
Eg6:【实际问题】:
【例1】:一只蚂蚁从地面开始爬树,它每天不停地往上爬,不幸的是,它每天白天能往上爬3米,可是一到夜里就要滑下2米,但是蚂蚁还是坚持往上爬,这棵树高是20米,蚂蚁从清晨开始从地面往上爬,它需要几天才能爬到树的最高处?( )
A.
17天
B.
18天
C.
19天
D.
20天
【跟踪练习】:一只蚂蚁从地面开始爬树,它每天不停地往上爬,不幸的是,它每天白天能往上爬5米,可是一到夜里就要滑下3米,但是蚂蚁还是坚持往上爬,这棵树高是50米,蚂蚁从清晨开始从地面往上爬,它需要
天才能爬到树的最高处
【例2】:不法商贩使用“八两称”坑害消费者,用这种称称东西,小吴以2.0元/kg的价格从不法商贩处买了8kg香蕉,那么他被商贩坑了 _________ 元钱.
【跟踪练习1】:“六?一”儿童节期间,某商场为吸引顾客,实行“买100送20,连环送”的活动,即顾客购物满100元,就可以获赠商场购物券20元,不足100元的部分不赠券,并且购物可以用现金,也可以用购物券.如果你有340元现金,在活动期间到该商场购物,最多可以获赠购物券累计为 _________ 元.
★【跟踪练习2】:老财主临终前将全部银元分给他的四个儿子.老大分得全部银元4等份中的1份,多出的1枚银元给了丫环;老二分得余下银元4等份中的1份,多出的1枚银元给了丫环;老三分得余下银元4等份中的1份,多出的1枚银元给了丫环;老四分得余下银元4等份中的1份,多出的1枚银元给了丫环;余下的银元又分成4等份,四个儿子各得一份,多出的1枚银元给了丫环.问老财主至少要有多少块银元才够分.
【跟踪练习3】:.股民小杨上星期五买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况(单位:元):
星期
一
二
三
四
五
每股涨跌
+220
+142
-080
-252
+130
(1)星期三收盘时,该股票涨或跌了多少元?
(2)本周内该股票的最高价是每股多少元?最底价是每股多少元?
(3)已知小杨了15‰的手续费,卖出时还需要付成交额的15‰的手续费和1‰的交易税如果小杨在星期五收盘前将全部股票卖出,则他的收益情况如何?
【跟踪练习4】:小明的妈妈在某玩具厂工作,厂里规定每个工人每周要生产某种玩具210个,平均每天生产30个,但由于种种原因,实际每天生产量与计划量相比有出入.下表是小明妈妈某周的生产情况(超产记为正、减产记为负):
(1)根据记录的数据可知小明妈妈星期三生产玩具__________个;
(2)根据记录的数据可知小明妈妈本周实际生产玩具__________个;
(3)该厂实行“每日计件工资制”。每生产一个玩具可得工资5元,若超额完成任务,则超过部分每个另奖3元;少生产一个则倒扣2元,那么小明妈妈这一周的工资总额是多少元?
(4)若将上面第(3)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,在此方式下小明妈妈这一周的工资与按日计件的工资哪一个更多?请说明理由.
Eg7:【类比推理类问题】:
【例】:为了求的值,可令,则
,因此,,所以.
即.
仿照以上的过程,计算:
=
.
【跟踪练习1】:阅读下面一段:计算1+5+52+53…+599+5100
观察发现,上式从第二项起,每项都是它前面一项的5倍,如果将上式各项都乘以5,所得新算式中除个别项外,其余与原式中的项相同,于是两式相减将使差易于计算.
解:设S=1+5+52+53…+599+5100,①
则5S=5+52+…+5100+5101,②
由②﹣①得4S=5101﹣1,则S=.
上面计算用的方法称为“错位相减法”,如果一列数,从第二项起每一项与前一项之比都相等(本例中是都等于5),那么这列数的求和问题,均可用上述“错位相减”法来解决.
下面请你观察算式1++++…+是否具备上述规律?若是,请你尝试用“错位相减”法计算上式的结果.
【跟踪练习2】:观察下列等式:,,,将以上三个等式两边分别相加得:
(1)猜想并写出:= _________ ;
(2)直接写出下列各式的计算结果:
①= _________ ;
②= _________ .
(3)探究并计算:.
Eg8:【阅读理解类问题】:
【例】:在解决数学问题的过程中,我们常用到
“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.
【提出问题】三个有理数满足,求的值.
【解决问题】[来m]
解:由题意,得三个有理数都为正数或其中一个为正数,另两个为负数.
①都是正数,即时,则;
②当中有一个为正数,另两个为负数时,不妨设,则
.
综上所述,值为3或-1.
【探究】请根据上面的解题思路解答下面的问题:
(1)三个有理数满足,求的值;
(2)若为三个不为0的有理数,且,求的值.
【跟踪练习1】:我们知道,表示数对应的点到原点的距离,这是绝对值的几何意义.进一步地,数轴上两个点分别表示数,那么.利用此结论,回答下列问题:
数轴上表示2和5的两点之间的距离是,数轴上表示-2和-5的两点之间的距离是
,
数轴上表示1和-3的两点之间的距离是
;
(2)数轴上表示和-1的两点之间的距离是
,如果=2,那么的值为
;[来
(3)写出表示的几何意义:
,该式的最小值为
;
(4)求的最小值.
.
【跟踪练习2】:阅读:已知点
A、B
在数轴上分别表示有理数、,A、B
两点之间的距离
表示为|AB|=||.
理解:
(1)数轴上表示
2和3的两点之间的距离是;
(2)数轴上表示
x
和5的两点
A
和
B
之间的距离是;
(3)代数式|x3|+|x+5|最小值是.
应用:如图,一条公路经过某个科技园区,该园区内有三家公司A、B、C分别位于公路的两侧,现要在园区内建一个公交站点H,已知AB=2000m,BC=3000m,问公交站点H建在图中何处,才能使得站点H到四个公司路程之和最短?最短路程是多少?请你仿照上面列式计算。
k.Com]
Eg9:【其他类问题】:
【例】:如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,若没有左右移动则记为0;第二个数表示上下方向,若没有上下移动则记为0.那么图中(9分)
(1)A→D(
,
),C→B(
,
),D→
(-3,+2);
(2)若贝贝的行走路线为A→B→D→C,请计算贝贝走过的路程;
(
3)若贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(+2,-1),(-1,+3),
(-2,-1),请在上图中标出妮妮的位置E点.
(4)在(3)中贝贝若每走1m需消耗2.5焦耳的能量,
则贝贝寻找妮妮过程中共需消耗多少焦耳的能量?
【跟踪练习1】:为确保信息安全,信息需加密传输,发送方由明文?密文(加密),接收方由密文?明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d.例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为 _________ .
【跟踪练习2】:已知两数、互为相反数,、互为倒数,的绝对值是2,
求的值。
【跟踪练习3】:若|x|=2,y2=9,且x>0,y<0,则x+y= _________ .
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
