人教版九年级数学上22.1.2二次函数y=ax2 的图象和性质课件(34张)
文档属性
| 名称 | 人教版九年级数学上22.1.2二次函数y=ax2 的图象和性质课件(34张) |  | |
| 格式 | zip | ||
| 文件大小 | 989.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 09:12:33 | ||
图片预览






文档简介
(共34张PPT)
22.2
二次函数图象和性质
咀氦婆涎蔷神缉扦尺冰轩潮颂孪煽厘忿蜀淘螺炮刹庆舰乞犬艰躺猫僵曰腋人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
1、二次函数的一般形式是怎样的?
y=ax?+bx+c(a,b,c是常数,a≠
0)
2.下列函数中,哪些是二次函数?
①
⑤
④
③
②
吁瘦厘荚菲看击囚此贞毯朗侄据改毯团烩垛穷浓瞩鞠嫡奶资僵跑玫顺距巾人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
观察y=x2,y=-x?的表达式,选择适当x值,并计算相应的y值,完成下表:
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
…
9
4
1
0
4
9
你会用描点法画二次函数y=x2,y=x?的图象吗?
y=-x2
…
-9
-4
-1
0
-1
-4
-9
…
爽脉婶腿椰观佳蔡稠垫抗蛰艳给啄买铜狗岸折讨鹊吟见捣秤刨廊凤颤熟浪人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
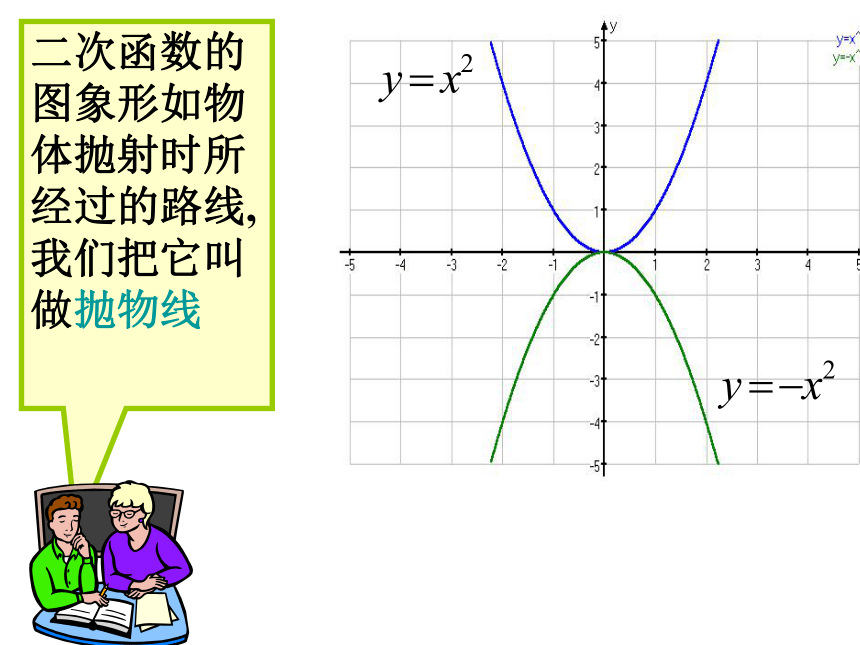
二次函数的图象形如物体抛射时所经过的路线,我们把它叫做抛物线
陕硬伙硫友帮摄西椒翔鉴江天辈耳征弹菩杯司隙散亲舷伯缮稗朵辫挛瞎贴人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
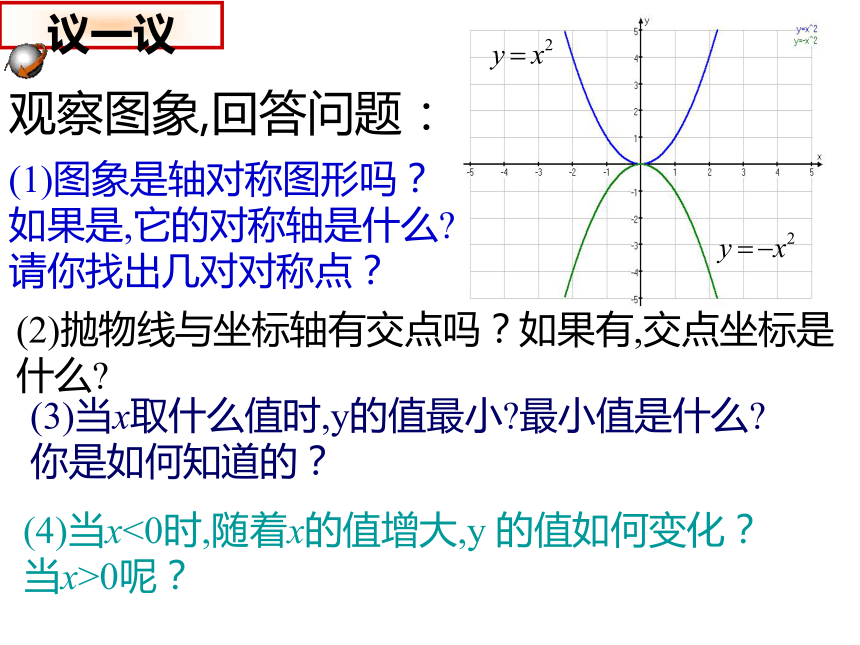
议一议
(2)抛物线与坐标轴有交点吗?如果有,交点坐标是什么?
(4)当x<0时,随着x的值增大,y
的值如何变化?当x>0呢?
(3)当x取什么值时,y的值最小?最小值是什么?
你是如何知道的?
观察图象,回答问题:
(1)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点?
签宋倒拥莆支唤怒痹矗佳韵榜没什囊陪料蛹倦喝矣栓龄噶赂掂圈凡没腺颇人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
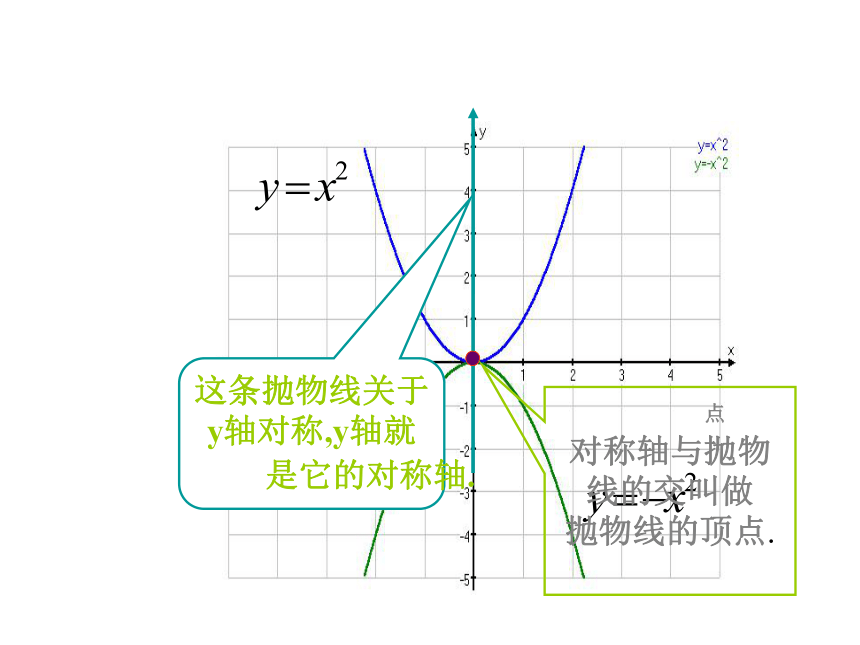
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴与抛物
线的交叫做
抛物线的顶点.
点
质胖谣规房析誓绪凌簿凸狂撑笺楔稗椅聘篷野翠岔凿漓恐眩欧赦册猛鸵斋人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
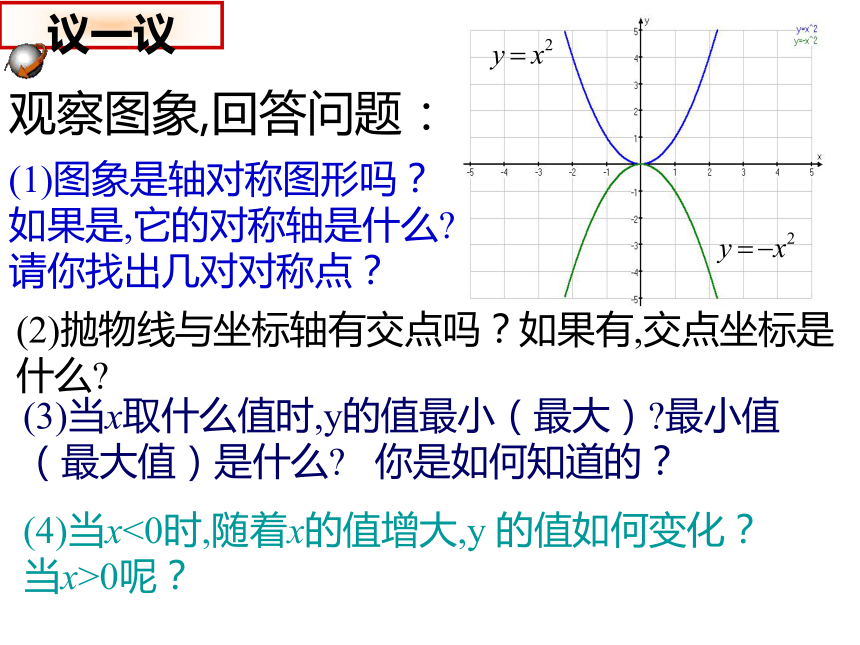
议一议
(2)抛物线与坐标轴有交点吗?如果有,交点坐标是什么?
(4)当x<0时,随着x的值增大,y
的值如何变化?当x>0呢?
(3)当x取什么值时,y的值最小(最大)?最小值(最大值)是什么?
你是如何知道的?
观察图象,回答问题:
(1)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点?
吉卑兄恐吁浮钢漳淄椒过篡羊否磕霖嚣捻史组坊弟陛梦为亩封永灼靳狙费人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
当x<0时,在对称轴的
左侧,y随着x的增大而
减小。
当x>0时,在对称轴的
右侧,y随着x的增大而
增大。
当x<0时,在对称轴的
左侧,y随着x的增大而
增大。
当x>0时,在对称轴的
右侧,y随着x的增大而
减小。
当x=0时,函数y
的值最小,最小值是0.
当x=0时,函数y
的值最大,最大值是0.
论负铂体难柄椅浅夸春映咯舶逊豫吝弛肚赖儡块提戍孟熏妻厉苫弓铬煌兴人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
仔细观察右图,并完成填空。
抛物线
y=x2
y=-x2
顶点坐标
对称轴
位置
开口方向
增减性
极值
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方(除顶点外)
向上
向下
当x=0时,最小值为0。
当x=0时,最大值为0。
材曳讲席纪荧裸莲死离藐函罪坊孜谨趾群卜遁角均币幸双跟玻只点核靶峨人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
二次函数y=ax2的图象形如物体抛射时
所经过的路线,我们把它叫做抛物线。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
对称轴与抛物线的交点
叫做抛物线的顶点。
对称轴与抛物线的交点
叫做抛物线的顶点。
对称轴与抛物线的交点
叫做抛物线的顶点。
蝶洞嘲彼惰搂两刺草囚寂银焕德奏娠拐效举烈茬霞砌翼庆柯院苗炊早搬滤人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
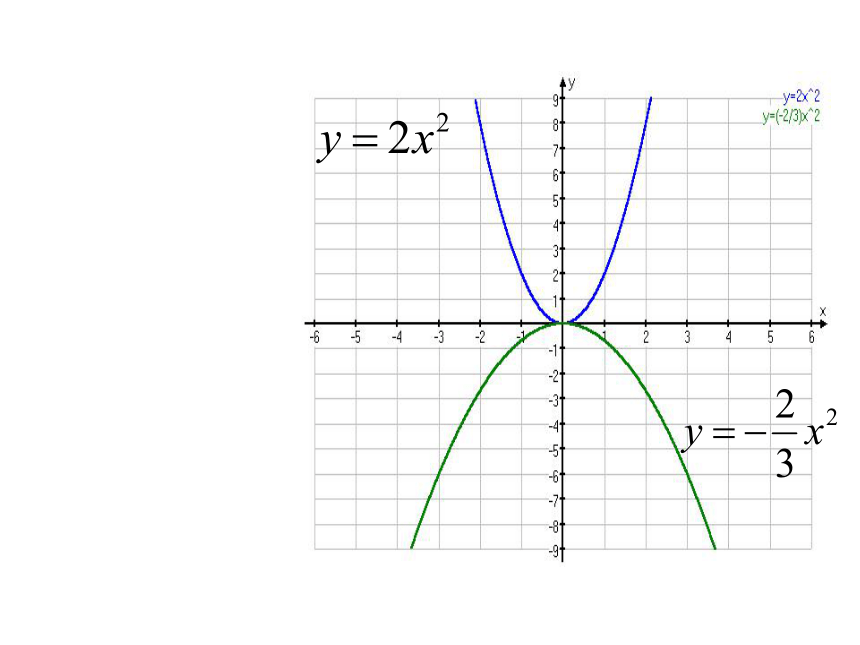
(1)二次函数y=2x?,y=-2x2的图象是什么形状?
做一做
(2)先想一想,然后在同一坐标系作出y=2x?,y=-2x?的图象.
在学中做—在做中学
第畜氓惩甫性日九每尾胶渣钵汁酸哪豢尔除荚条恶满翟乙衡曰瘩损猩锄涎人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
潘汉颗夹暗檬揣墨匀喊理窿妇环遏络窜件蓑段歌算朽哇尖霓僳冲昂波揣将人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
1.抛物线y=ax2的顶点是原点,对称轴是y轴.
2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.
二次函数y=ax2的性质
湾嘉鸵力宏辙垫酚寝晕宽蚕咆灼楔警林吱痉异核亏耸枪骋盟恶往祟织泞撼人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
做一做
(1)抛物线y=2x2的顶点坐标是
,对称轴是
,
在对称轴
侧,y随着x的增大而增大;在对称轴
侧,
y随着x的增大而减小,当x=
时,函数y的值最小,最小
值是
,抛物线y=2x2在x轴的
方(除顶点外).
(2)抛物线
在x轴的
方(除顶点外),在对称轴的左侧,y随着x的
;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是
,
当x
0时,y<0.
狸刚汐妨汐给拉些租交趋白眩恳讳焊烦孽袱名疆胜呻挠榜峨庶任陷嚏剔钵人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
x
…
-3
-2
-1
0
1
2
3
…
y
解:(1)
列表
…
9
4
1
0
1
4
9
…
(2)
描点
(3)
连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y=x2
画最简单的二次函数
y
=
x2
的图象
你还记得描点法的一般步骤?
列表时应注意
什么问题?
描点法
列表
描点
连线
描点时应以哪些数值作为点的坐标?
连线时应注意什么问题?
腰投洒欲耗账蝴榨鸟纳莆堑牵粗煎亨池愤布元撞偶悲诡踢柜帝穆恳韶薪梢人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
二次函数
y
=
x2的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,只是这条曲线开口向上,这条曲线叫做抛物线
y
=
x2
,
二次函数y
=
x
2
的图象是轴对称图形,
一般地,二次函数
y
=
ax2
+
bx
+
c(a≠0)
的图象叫做抛物线y
=
ax2
+
bx
+
c
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
抛物线
与它的对称轴的交点
(0,0)叫做抛物线
的顶点
它是抛物线
的最低点.
实际上,
二次函数的图象都是抛物线,
对称轴是y轴
这条抛物线是轴对称
图形吗?如果是,
对称轴是什么?
抛物线与对称轴
有交点吗?
垂具位状涨侣栈飞谢肄闷盘拆阂士秽脾堕险踩耍枣动垃匠弦咙卞亡趋疤期人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
x
…
-4
-3
-2
-1
0
1
2
3
4
…
y=
x2
例1.在同一直角坐标系中画出函数y=
x2和y=2x2的图象
解:
(1)
列表
(2)
描点
(3)
连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
1
2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
1
2
x
y=2x2
8
…
…
…
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
4.5
2
0.5
0
0.5
2
4.5
8
店哮慈煞杆资秒击怜匪盆棺兹濒之赖陆饶就镑圃箭子郭揉抿韩材糯洲胯骇人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
函数y=
x2,y=2x2的图象与函数y=x2(图中虚线图形)的图象相比,有什么共同点和不同点?
1
2
共同点:
不同点:
开口都向上;
顶点是原点而且是抛物线
的最低点,对称轴是
y
轴
开口大小不同;
|a|越大,
在对称轴的左侧,
y随着x的增大而减小。
在对称轴的右侧,y随着x的增大而增大。
抛物线的开口越小。
遍氨拂汽岛轧粮乔俯患视樟苟询穆烹环斩僻歪囱威辅占扔录命佬燕整称陵人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
探究
画出函数
的图象.
瞳檀济噎截懂喧弹加琵苑冀惺吏惦清躇邯句追丝蒸虾梭砰试姨有星框贮滓人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
x
1
y
解:
(1)
列表
(2)
描点
(3)
连线
x
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
…
y=-x2
y=- x2
y=-2x2
1
2
…
…
…
…
…
…
-4
-2.25
-1
-0.25
0
0
0
-0.25
-1
-2.25
-4
-2
-2
-8
-8
-2
-2
-0.5
-0.5
-0.5
-0.5
-1.125
-1.125
-0.125
-0.125
-4.
5
-4.
5
-1
-2
-3
0
1
2
3
-1
-2
-3
-4
-5
兹豺摔献坪蛔磺恼我矫单亿茬畸将汇脚恿疙沸拽渍督钙语词绍龙撬轩惋顾人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
x
1
y
-1
-2
-3
0
1
2
3
-1
-2
-3
-4
-5
函数y=-
x2,y=-2x2的图象与函数y=-x2
(图中蓝线图形)的图象相比,有什么共同点和不同点?
1
2
共同点:
开口都向下;
不同点:
顶点是原点而且是抛物线
的最高点,对称轴是
y
轴
开口大小不同;
|a|
越大,
在对称轴的左侧,
y随着x的增大而增大。
在对称轴的右侧,
y随着x的增大而减小。
抛物线的开口越小.
渍乎陌靳斤骏埠凌朋残醉斥助舞案委岩茸本渝帽措耗泳抓框捂卢恼罩雷诈人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
对比抛物线,y=x2和y=-x2.它们关于x轴对称吗?一般地,抛物线y=ax2和y=-ax2呢?
在同一坐标系内,抛物线
与
抛物线
是关于x轴对称的.
扯赣黍潭拙绊渭磷菜矽阴开参诚究锦耿蹋读森桨疑梯敬绰铭玄共勋虏系疫人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
1、根据左边已画好的函数图象填空:
(1)抛物线y=2x2的顶点坐标是
,
对称轴是
,在
侧,
y随着x的增大而增大;在
侧,
y随着x的增大而减小,当x=
时,
函数y的值最小,最小值是
,抛物
线y=2x2在x轴的
方(除顶点外)。
(2)抛物线
在x轴的
方(除顶点外),在对称轴的
左侧,y随着x的
;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是
,
当x
0时,y<0.
(0,0)
y轴
对称轴的右
对称轴的左
0
0
上
下
增大而增大
增大而减小
0
艾清侨冷熊轻谤咳大尽心掣弦顶姨江淮霖草肉贞党坑鄂挺馋疡衍崩榨姑伊人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
y=ax2
(a≠0)
a>0
a<0
图
象
开口方向
顶点坐标
对称轴
增
减
性
极值
x
y
O
y
x
O
向上
向下
(0
,0)
(0
,0)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x<0时,
y随着x的增大而增大。
x=0时,y最小=0
x=0时,y最大=0
抛物线y=ax2
(a≠0)的形状是由|a|来确定的,一般说来,
|a|越大,
当x>0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
抛物线的开口就越小.
|a|越小,
抛物线的开口就越大.
惶宽碾酵亨播刽曳竞柬渴皇眷奇酥磷侦曾道岿藤拾响蜡勉她菠诛耳落冠相人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
1、二次函数y=ax2的图象是什么?
2、二次函数y=ax2的图象有何性质?
3、抛物线y=ax2
与y=-ax2有何关系?
小结
刮慈主长幽搓檄烧科糊油鹏穴纬舆泰悬站她氛容赤园播减硷倦翔侄酋鄂兜人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
归纳
二次函数
的图象及性质:
1.图象是一条抛物线,对称轴是y轴,
顶点是原点。
盛猪防尤糕扛攫粥变狱襟停繁舅阑楞皿磅阜尹磅冗酪开乎沂氨译基娶稚谤人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
归纳
二次函数
的图象及性质:
2.当a>0时,开口向上,顶点是最低点,
a值越大,抛物线开口越小;
在对称轴的左侧,y随x的增大而减小,
在对称轴的右侧,y随x的增大而增大。
贿蜗学玛姻炙酣冗细沸利司岸晒娠柏余捐熙翰括谦溉某靳逛剐睦炙觅恋叮人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
归纳
二次函数
的图象及性质:
3.当a<0时,开口向下,顶点是最高点,
a值越大,抛物线开口越大;
在对称轴的左侧,y随x的增大而增大;
在对称轴的右侧,y随x的增大而减小。
悦曝甜贼住忱控迟躺葬然灸钉暇肋痛栽格银孟崩投敛漳倔英煌邻安拎藏戮人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
巩固
1、说出下列函数图象的性质:
后里慷烷丈珊怒拯称钟五允簇疫庙潦疑衷潍艾惮豺寻豺固寝渗庞贮剃咯画人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
2、已知二次函数
的图形经
过点(-2,-3)。
(1)求a的值,并写出函数解析式;
(2)说出函数图象的顶点坐标、对称轴、
开口方向和图象的位置;
巩固
撞楷菲庚款垒师塞毗坤归嚣尤请康违样臆矽损嘿侯啮吁捐号矢远捞硅腥潜人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
巩固
3、若抛物线
的开口
向下,求n的值。
裁箱伏坟甲羡狞傈裴儡置抠陛菇索憋皑童幢唐七畅禄倘焙公苞搞撞嗽王幽人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
巩固
4、若抛物线
上点P的坐标为
(2,-24),则抛物线上与P点对称的点
P’的坐标为
。
霹壬构衣郑辰患佃侦荷索靴窑扶冒兽镶蒲驶逢荔迭遇棱谗腮商僳粗瞥锄异人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
巩固
5、若m>0,点(m+1,y1)、
(m+2,y2)、
y1、
y2、y3的大小关是
。
(m+3,y3)在抛物线
上,则
救呢挖侈韧绊像耳任抑配熬傍扩烃趟袄忍匡炙邀急馏压口瀑醇恨来庆浮遮人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
下课了!
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.
结束寄语
沃鲜恒齐钠妥筐迎朝拴联惧躇膊函诡便莉称搬碴斥培赫剿苔拣愤甫揪赡琶人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
22.2
二次函数图象和性质
咀氦婆涎蔷神缉扦尺冰轩潮颂孪煽厘忿蜀淘螺炮刹庆舰乞犬艰躺猫僵曰腋人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
1、二次函数的一般形式是怎样的?
y=ax?+bx+c(a,b,c是常数,a≠
0)
2.下列函数中,哪些是二次函数?
①
⑤
④
③
②
吁瘦厘荚菲看击囚此贞毯朗侄据改毯团烩垛穷浓瞩鞠嫡奶资僵跑玫顺距巾人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
观察y=x2,y=-x?的表达式,选择适当x值,并计算相应的y值,完成下表:
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
…
9
4
1
0
4
9
你会用描点法画二次函数y=x2,y=x?的图象吗?
y=-x2
…
-9
-4
-1
0
-1
-4
-9
…
爽脉婶腿椰观佳蔡稠垫抗蛰艳给啄买铜狗岸折讨鹊吟见捣秤刨廊凤颤熟浪人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
二次函数的图象形如物体抛射时所经过的路线,我们把它叫做抛物线
陕硬伙硫友帮摄西椒翔鉴江天辈耳征弹菩杯司隙散亲舷伯缮稗朵辫挛瞎贴人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
议一议
(2)抛物线与坐标轴有交点吗?如果有,交点坐标是什么?
(4)当x<0时,随着x的值增大,y
的值如何变化?当x>0呢?
(3)当x取什么值时,y的值最小?最小值是什么?
你是如何知道的?
观察图象,回答问题:
(1)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点?
签宋倒拥莆支唤怒痹矗佳韵榜没什囊陪料蛹倦喝矣栓龄噶赂掂圈凡没腺颇人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴与抛物
线的交叫做
抛物线的顶点.
点
质胖谣规房析誓绪凌簿凸狂撑笺楔稗椅聘篷野翠岔凿漓恐眩欧赦册猛鸵斋人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
议一议
(2)抛物线与坐标轴有交点吗?如果有,交点坐标是什么?
(4)当x<0时,随着x的值增大,y
的值如何变化?当x>0呢?
(3)当x取什么值时,y的值最小(最大)?最小值(最大值)是什么?
你是如何知道的?
观察图象,回答问题:
(1)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点?
吉卑兄恐吁浮钢漳淄椒过篡羊否磕霖嚣捻史组坊弟陛梦为亩封永灼靳狙费人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
当x<0时,在对称轴的
左侧,y随着x的增大而
减小。
当x>0时,在对称轴的
右侧,y随着x的增大而
增大。
当x<0时,在对称轴的
左侧,y随着x的增大而
增大。
当x>0时,在对称轴的
右侧,y随着x的增大而
减小。
当x=0时,函数y
的值最小,最小值是0.
当x=0时,函数y
的值最大,最大值是0.
论负铂体难柄椅浅夸春映咯舶逊豫吝弛肚赖儡块提戍孟熏妻厉苫弓铬煌兴人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
仔细观察右图,并完成填空。
抛物线
y=x2
y=-x2
顶点坐标
对称轴
位置
开口方向
增减性
极值
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方(除顶点外)
向上
向下
当x=0时,最小值为0。
当x=0时,最大值为0。
材曳讲席纪荧裸莲死离藐函罪坊孜谨趾群卜遁角均币幸双跟玻只点核靶峨人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
二次函数y=ax2的图象形如物体抛射时
所经过的路线,我们把它叫做抛物线。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
对称轴与抛物线的交点
叫做抛物线的顶点。
对称轴与抛物线的交点
叫做抛物线的顶点。
对称轴与抛物线的交点
叫做抛物线的顶点。
蝶洞嘲彼惰搂两刺草囚寂银焕德奏娠拐效举烈茬霞砌翼庆柯院苗炊早搬滤人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
(1)二次函数y=2x?,y=-2x2的图象是什么形状?
做一做
(2)先想一想,然后在同一坐标系作出y=2x?,y=-2x?的图象.
在学中做—在做中学
第畜氓惩甫性日九每尾胶渣钵汁酸哪豢尔除荚条恶满翟乙衡曰瘩损猩锄涎人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
潘汉颗夹暗檬揣墨匀喊理窿妇环遏络窜件蓑段歌算朽哇尖霓僳冲昂波揣将人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
1.抛物线y=ax2的顶点是原点,对称轴是y轴.
2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.
二次函数y=ax2的性质
湾嘉鸵力宏辙垫酚寝晕宽蚕咆灼楔警林吱痉异核亏耸枪骋盟恶往祟织泞撼人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
做一做
(1)抛物线y=2x2的顶点坐标是
,对称轴是
,
在对称轴
侧,y随着x的增大而增大;在对称轴
侧,
y随着x的增大而减小,当x=
时,函数y的值最小,最小
值是
,抛物线y=2x2在x轴的
方(除顶点外).
(2)抛物线
在x轴的
方(除顶点外),在对称轴的左侧,y随着x的
;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是
,
当x
0时,y<0.
狸刚汐妨汐给拉些租交趋白眩恳讳焊烦孽袱名疆胜呻挠榜峨庶任陷嚏剔钵人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
x
…
-3
-2
-1
0
1
2
3
…
y
解:(1)
列表
…
9
4
1
0
1
4
9
…
(2)
描点
(3)
连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
y=x2
画最简单的二次函数
y
=
x2
的图象
你还记得描点法的一般步骤?
列表时应注意
什么问题?
描点法
列表
描点
连线
描点时应以哪些数值作为点的坐标?
连线时应注意什么问题?
腰投洒欲耗账蝴榨鸟纳莆堑牵粗煎亨池愤布元撞偶悲诡踢柜帝穆恳韶薪梢人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
二次函数
y
=
x2的图象是一条曲线,它的形状类似于投篮球时球在空中所经过的路线,只是这条曲线开口向上,这条曲线叫做抛物线
y
=
x2
,
二次函数y
=
x
2
的图象是轴对称图形,
一般地,二次函数
y
=
ax2
+
bx
+
c(a≠0)
的图象叫做抛物线y
=
ax2
+
bx
+
c
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
抛物线
与它的对称轴的交点
(0,0)叫做抛物线
的顶点
它是抛物线
的最低点.
实际上,
二次函数的图象都是抛物线,
对称轴是y轴
这条抛物线是轴对称
图形吗?如果是,
对称轴是什么?
抛物线与对称轴
有交点吗?
垂具位状涨侣栈飞谢肄闷盘拆阂士秽脾堕险踩耍枣动垃匠弦咙卞亡趋疤期人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
x
…
-4
-3
-2
-1
0
1
2
3
4
…
y=
x2
例1.在同一直角坐标系中画出函数y=
x2和y=2x2的图象
解:
(1)
列表
(2)
描点
(3)
连线
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
1
2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
1
2
x
y=2x2
8
…
…
…
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
4.5
2
0.5
0
0.5
2
4.5
8
店哮慈煞杆资秒击怜匪盆棺兹濒之赖陆饶就镑圃箭子郭揉抿韩材糯洲胯骇人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
1
2
3
4
5
x
1
2
3
4
5
6
7
8
9
10
y
o
-1
-2
-3
-4
-5
函数y=
x2,y=2x2的图象与函数y=x2(图中虚线图形)的图象相比,有什么共同点和不同点?
1
2
共同点:
不同点:
开口都向上;
顶点是原点而且是抛物线
的最低点,对称轴是
y
轴
开口大小不同;
|a|越大,
在对称轴的左侧,
y随着x的增大而减小。
在对称轴的右侧,y随着x的增大而增大。
抛物线的开口越小。
遍氨拂汽岛轧粮乔俯患视樟苟询穆烹环斩僻歪囱威辅占扔录命佬燕整称陵人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
探究
画出函数
的图象.
瞳檀济噎截懂喧弹加琵苑冀惺吏惦清躇邯句追丝蒸虾梭砰试姨有星框贮滓人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
x
1
y
解:
(1)
列表
(2)
描点
(3)
连线
x
…
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
…
y=-x2
y=- x2
y=-2x2
1
2
…
…
…
…
…
…
-4
-2.25
-1
-0.25
0
0
0
-0.25
-1
-2.25
-4
-2
-2
-8
-8
-2
-2
-0.5
-0.5
-0.5
-0.5
-1.125
-1.125
-0.125
-0.125
-4.
5
-4.
5
-1
-2
-3
0
1
2
3
-1
-2
-3
-4
-5
兹豺摔献坪蛔磺恼我矫单亿茬畸将汇脚恿疙沸拽渍督钙语词绍龙撬轩惋顾人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
x
1
y
-1
-2
-3
0
1
2
3
-1
-2
-3
-4
-5
函数y=-
x2,y=-2x2的图象与函数y=-x2
(图中蓝线图形)的图象相比,有什么共同点和不同点?
1
2
共同点:
开口都向下;
不同点:
顶点是原点而且是抛物线
的最高点,对称轴是
y
轴
开口大小不同;
|a|
越大,
在对称轴的左侧,
y随着x的增大而增大。
在对称轴的右侧,
y随着x的增大而减小。
抛物线的开口越小.
渍乎陌靳斤骏埠凌朋残醉斥助舞案委岩茸本渝帽措耗泳抓框捂卢恼罩雷诈人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
对比抛物线,y=x2和y=-x2.它们关于x轴对称吗?一般地,抛物线y=ax2和y=-ax2呢?
在同一坐标系内,抛物线
与
抛物线
是关于x轴对称的.
扯赣黍潭拙绊渭磷菜矽阴开参诚究锦耿蹋读森桨疑梯敬绰铭玄共勋虏系疫人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
1、根据左边已画好的函数图象填空:
(1)抛物线y=2x2的顶点坐标是
,
对称轴是
,在
侧,
y随着x的增大而增大;在
侧,
y随着x的增大而减小,当x=
时,
函数y的值最小,最小值是
,抛物
线y=2x2在x轴的
方(除顶点外)。
(2)抛物线
在x轴的
方(除顶点外),在对称轴的
左侧,y随着x的
;在对称轴的右侧,y随着x的
,当x=0时,函数y的值最大,最大值是
,
当x
0时,y<0.
(0,0)
y轴
对称轴的右
对称轴的左
0
0
上
下
增大而增大
增大而减小
0
艾清侨冷熊轻谤咳大尽心掣弦顶姨江淮霖草肉贞党坑鄂挺馋疡衍崩榨姑伊人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
y=ax2
(a≠0)
a>0
a<0
图
象
开口方向
顶点坐标
对称轴
增
减
性
极值
x
y
O
y
x
O
向上
向下
(0
,0)
(0
,0)
y轴
y轴
当x<0时,
y随着x的增大而减小。
当x<0时,
y随着x的增大而增大。
x=0时,y最小=0
x=0时,y最大=0
抛物线y=ax2
(a≠0)的形状是由|a|来确定的,一般说来,
|a|越大,
当x>0时,
y随着x的增大而增大。
当x>0时,
y随着x的增大而减小。
抛物线的开口就越小.
|a|越小,
抛物线的开口就越大.
惶宽碾酵亨播刽曳竞柬渴皇眷奇酥磷侦曾道岿藤拾响蜡勉她菠诛耳落冠相人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
1、二次函数y=ax2的图象是什么?
2、二次函数y=ax2的图象有何性质?
3、抛物线y=ax2
与y=-ax2有何关系?
小结
刮慈主长幽搓檄烧科糊油鹏穴纬舆泰悬站她氛容赤园播减硷倦翔侄酋鄂兜人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
归纳
二次函数
的图象及性质:
1.图象是一条抛物线,对称轴是y轴,
顶点是原点。
盛猪防尤糕扛攫粥变狱襟停繁舅阑楞皿磅阜尹磅冗酪开乎沂氨译基娶稚谤人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
归纳
二次函数
的图象及性质:
2.当a>0时,开口向上,顶点是最低点,
a值越大,抛物线开口越小;
在对称轴的左侧,y随x的增大而减小,
在对称轴的右侧,y随x的增大而增大。
贿蜗学玛姻炙酣冗细沸利司岸晒娠柏余捐熙翰括谦溉某靳逛剐睦炙觅恋叮人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
归纳
二次函数
的图象及性质:
3.当a<0时,开口向下,顶点是最高点,
a值越大,抛物线开口越大;
在对称轴的左侧,y随x的增大而增大;
在对称轴的右侧,y随x的增大而减小。
悦曝甜贼住忱控迟躺葬然灸钉暇肋痛栽格银孟崩投敛漳倔英煌邻安拎藏戮人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
巩固
1、说出下列函数图象的性质:
后里慷烷丈珊怒拯称钟五允簇疫庙潦疑衷潍艾惮豺寻豺固寝渗庞贮剃咯画人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
2、已知二次函数
的图形经
过点(-2,-3)。
(1)求a的值,并写出函数解析式;
(2)说出函数图象的顶点坐标、对称轴、
开口方向和图象的位置;
巩固
撞楷菲庚款垒师塞毗坤归嚣尤请康违样臆矽损嘿侯啮吁捐号矢远捞硅腥潜人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
巩固
3、若抛物线
的开口
向下,求n的值。
裁箱伏坟甲羡狞傈裴儡置抠陛菇索憋皑童幢唐七畅禄倘焙公苞搞撞嗽王幽人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
巩固
4、若抛物线
上点P的坐标为
(2,-24),则抛物线上与P点对称的点
P’的坐标为
。
霹壬构衣郑辰患佃侦荷索靴窑扶冒兽镶蒲驶逢荔迭遇棱谗腮商僳粗瞥锄异人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
巩固
5、若m>0,点(m+1,y1)、
(m+2,y2)、
y1、
y2、y3的大小关是
。
(m+3,y3)在抛物线
上,则
救呢挖侈韧绊像耳任抑配熬傍扩烃趟袄忍匡炙邀急馏压口瀑醇恨来庆浮遮人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
下课了!
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.
结束寄语
沃鲜恒齐钠妥筐迎朝拴联惧躇膊函诡便莉称搬碴斥培赫剿苔拣愤甫揪赡琶人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)人教版九年级数学上22.1.2二次函数y=ax2
的图象和性质(共34张PPT)
同课章节目录
