苏科版七年级数学上册 第2章 有理数 章末培优训练卷(word版,无答案)
文档属性
| 名称 | 苏科版七年级数学上册 第2章 有理数 章末培优训练卷(word版,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 648.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 19:40:37 | ||
图片预览


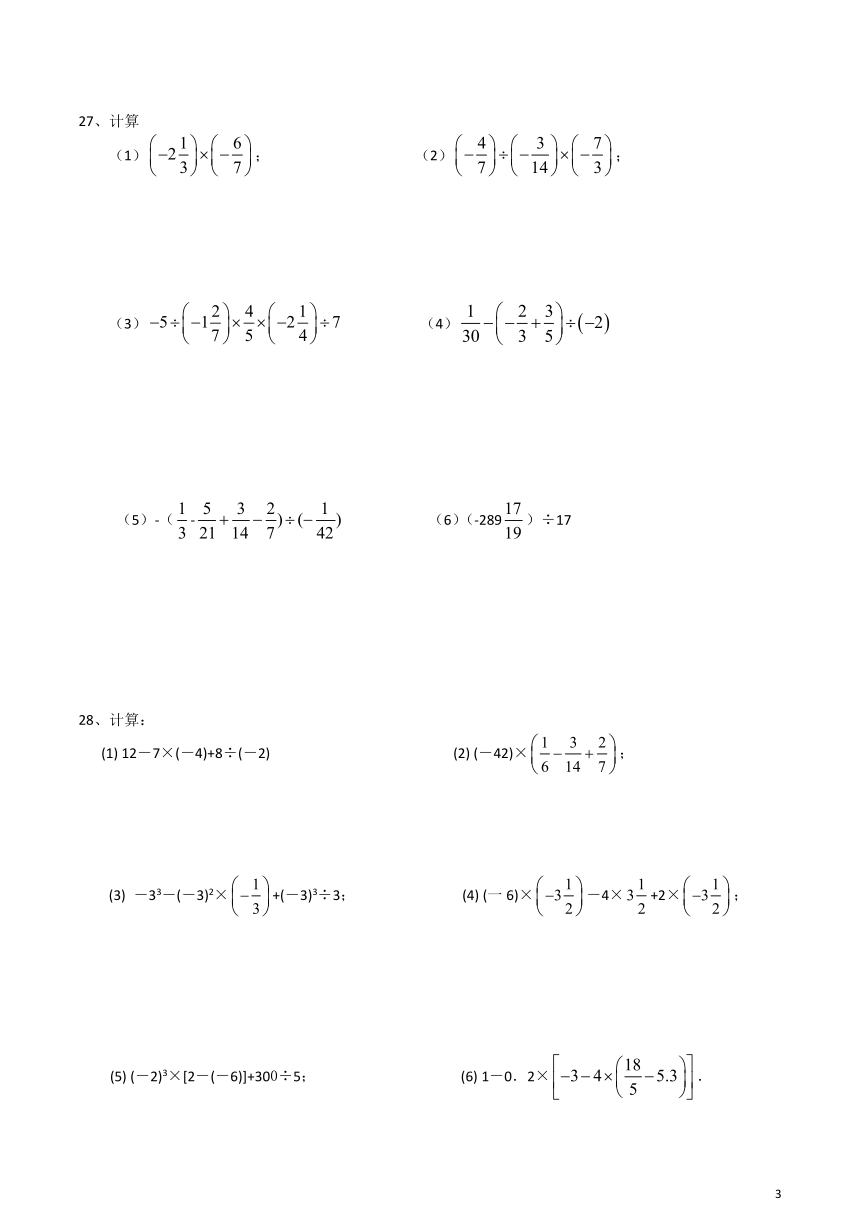

文档简介
2020-2021苏科版七年级数学上册第2章有理数章末培优训练卷
一、选择题
1、下列说法中正确的是
(
)
A.有最小的正数
B.有最大的负数
C.有最小的整数
D.有最小的正整数
2、纽约、悉尼与北京时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京时间晚的时数):
城市
悉尼
纽约
时差/时
+2
-13
当北京
6
月
15
日
23
时,悉尼、纽约的时间分别是(
)
A.6
月
16
日
1
时;6
月
15
日
10
时
B.6
月
16
日
1
时;6
月
14
日
10
时
C.6
月
15
日
21
时;6
月
15
日
10
时
D.6
月
15
日
21
时;6
月
16
日
12
时
3、下列说法中,正确的是(
)
A.有理数就是正数和负数的统称
B.零不是自然数,但是正数
C.一个有理数不是整数就是分数
D.正分数、零、负分数统称分数
4、在,3.14,0,0.313
113
111.…,0.43五个数中分数有(
)个.
A.1
B.2
C.3
D.4
5、在数轴上与原点的距离等于
2
的点表示的数是(??
)
A.?2???????????????????????????????????B.?﹣2???????????????????????????????????C.?﹣1
或
3???????????????????????????????????D.?﹣2
或
2
6、如图,将一刻度尺放在数轴上.
①若刻度尺上
0cm
和
4cm
对应数轴上的点表示的数分别为
1
和
5,则
1cm
对应数轴上的点表示的数是
2;
②若刻度尺上
0cm
和
4cm
对应数轴上的点表示的数分别为
1
和
9,则
1cm
对应数轴上的点表示的数是
3;
③若刻度尺上
0cm
和
4cm
对应数轴上的点表示的数分别为-2
和
2,则
1cm
对应数轴上的点表示的数是-1;
④若刻度尺上
0cm
和
4
cm
对应数轴上的点表示的数分别为-1
和
1,则
1cm
对应数轴上的点表示的数是-0.5.
上述结论中,所有符合题意结论的序号是(??
)
A.?①②???????????????????B.?②④???????????????C.?①②③?????????????????????D.?①②③④
7、能使等式|2x﹣3|+2|x﹣2|=1成立的x的取值可以是( )
A.0
B.1
C.2
D.3
8、若a=4,|b|=3,且a,b异号,则a-b的值为( )
A.
B.
C.
5
D.
9、若a+b=0,则下列各组中不互为相反数的数是( )
A.
和
B.
和
C.
和
D.
和
10、如果三个数的和大于0,积小于0,那么这三个数中负数有(
)
A.
0个
B.
1个
C.
2个
D.
3个
11、已知,则式子:(
)
A.3
B.或1
C.或3
D.1
12、如果,那么有(
)
A.
B.
C.
D.
二、填空题
13、仔细思考下列各对量:①胜两局与负三局;②气温升高
3℃与气温为﹣3℃;
③盈利
3
万元与支出
3
万元;④甲、乙两支球队组织了两场篮球比赛,甲、乙两
队的比分分别为
65:60
与
60:65.其中具有相反意义的量有
14、在一次全市的数学监测中某6名学生的成绩与全市学生的平均分80的差分别为5,﹣2,8,11,5,﹣6,则这6名学生的平均成绩为
分.
15、有六个位:0.123,(﹣1.5)3,3.1416,,﹣2π,0.1020020002…,若其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z=______.
16、在﹣2、,4.121121112、π﹣3.14,、0.5中,是无理数的为
.
17、如图,点A,B,C为数轴上的3点,请回答下列问题:
(1)将点A向右平移3个单位长度后,点
表示的数最小;
(2)将点C向左平移6个单位长度后,点A表示的数比点C表示的数小
;
(3)将点B向左平移2个单位长度后,点B与点C的距离是
.
18、数轴上表示的数是整数的点称为整点,某数轴的单位长度是1cm,若在这个数轴上任意画出一条
长2015cm的线段AB,则线段AB盖住的整点的个数是
.
19、已知:[x]表示不超过x的最大整数.例:[4.8]=4,[-0.8]=-1.现定义:{x}=x-[x],
例:{1.5}=1.5-[1.5]=0.5,则{3.9}+{-1.8}-{1}=______.
20、a、b在的位置如图所示,则数a、-a、b、-b的大小关系为______
21、已知且,那么
.
22、已知且,那么=
.
23、在学习了《有理数及其运算》以后,小明和小亮一起玩“24点”游戏,规则如下:从一副扑克牌(去掉大、小王)中任意抽取4张,根据牌面上的数字进行混合运算(每张牌只能用一次),使得运算结果为24或-24,其中红色扑克牌代表负数,黑色扑克牌代表正数,分别代表11、12、13.现在小亮抽到的扑克牌代表的数分别是:3、-4、-6、10,请你帮助他写一个算式,使其运算结果等于24或-24__________.
24、已知光在真空中的传播速度是,1年约为,则1光年(光1年所走的路程)约为
m.(用科学记数法表示)
三、解答题
25、在数轴上表示下列各数,并把它们按照从小到大的顺序排列.,,0,,
26、计算:
(1)(-32)+(+16)
(2)-0.5+3+2.6-5+1.15;
(3)-+-+-;
(4)(-2.5)-(+2.7)-(-1.6)-(-2.7)+(+2.4)
(5)-│4-6│-[(-2)-(-0.8)-│-2│];
(6)-32+5-3-5+12
27、计算
(1);
(2);
(3)
(4)
(5)-(-
(6)(-289)÷17
28、计算:
(1)
12-7×(-4)+8÷(-2)
(2)
(-42)×;
(3)
-33-(-3)2×+(-3)3÷3;
(4)
(一6)×-4×+2×;
(5)
(-2)3×[2-(-6)]+300÷5;
(6)
1-0.2×.
(7)
(8)
29、阅读下面的解答过程:
计算:
观察发现,上式从第二项起,每一项都是它前一项的5倍,如果上式各项都乘5,所得新算式中除个别项外,其余与原式中的项都相同,于是两式相减将使差易于计算.
解:设①,
则②,
②-①,得
上面计算用的方法称为“错位相减法”,如果一列数,从第二项起每一项与前一项之比都相等(本例题中都等于5),那么这列数的求和问题均可用上述“错位相减法”来解决.
请你观察算式:是否具备上述规律?若具备,请你尝试“错位相减法”计算上式的结果.
30、某灯具厂计划一天生产300盏景观灯,但由于各种原因,实际每天生产景观灯数与计划每天生产景观灯数相比有出入.下表是某周的生产情况(增产记为正、减产记为负):
星期
一
二
三
四
五
六
日
增减
(1)求该厂本周实际生产景观灯的盏数;
(2)求产量最多的一天比产量最少的一天多生产景观灯的盏数;
(3)该厂实行每日计件工资制,每生产一盏景观灯可得60元,若超额完成任务,则超过部分每盏另奖20元,若未能完成任务,则少生产一盏扣25元,那么该厂工人这一周的工资总额是多少元?
2020-2021苏科版七年级数学上册第2章有理数章末培优训练卷(答案)
一、选择题
1、下列说法中正确的是
(
D
)
A.有最小的正数
B.有最大的负数
C.有最小的整数
D.有最小的正整数
2、纽约、悉尼与北京时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京时间晚的时数):
城市
悉尼
纽约
时差/时
+2
-13
当北京
6
月
15
日
23
时,悉尼、纽约的时间分别是(A
)
A.6
月
16
日
1
时;6
月
15
日
10
时
B.6
月
16
日
1
时;6
月
14
日
10
时
C.6
月
15
日
21
时;6
月
15
日
10
时
D.6
月
15
日
21
时;6
月
16
日
12
时
3、下列说法中,正确的是(
C
)
A.有理数就是正数和负数的统称
B.零不是自然数,但是正数
C.一个有理数不是整数就是分数
D.正分数、零、负分数统称分数
4、在,3.14,0,0.313
113
111.…,0.43五个数中分数有(
B
)个.
A.1
B.2
C.3
D.4
5、在数轴上与原点的距离等于
2
的点表示的数是(??D
)
A.?2???????????????????????????????????B.?﹣2???????????????????????????????????C.?﹣1
或
3???????????????????????????????????D.?﹣2
或
2
6、如图,将一刻度尺放在数轴上.
①若刻度尺上
0cm
和
4cm
对应数轴上的点表示的数分别为
1
和
5,则
1cm
对应数轴上的点表示的数是
2;
②若刻度尺上
0cm
和
4cm
对应数轴上的点表示的数分别为
1
和
9,则
1cm
对应数轴上的点表示的数是
3;
③若刻度尺上
0cm
和
4cm
对应数轴上的点表示的数分别为-2
和
2,则
1cm
对应数轴上的点表示的数是-1;
④若刻度尺上
0cm
和
4
cm
对应数轴上的点表示的数分别为-1
和
1,则
1cm
对应数轴上的点表示的数是-0.5.
上述结论中,所有符合题意结论的序号是(??D
)
A.?①②???????????????????B.?②④???????????????C.?①②③?????????????????????D.?①②③④
7、能使等式|2x﹣3|+2|x﹣2|=1成立的x的取值可以是( )
A.0
B.1
C.2
D.3
【分析】直接利用绝对值的性质把x的值分别代入求出答案.
【解析】A、当x=0时,原式=3+4=7,不合题意;
B、当x=1时,原式=1+2=3,不合题意;
C、当x=2时,原式=1+0=1,符合题意;
D、当x=3时,原式=3+2=5,不合题意;
故选:C.
8、若a=4,|b|=3,且a,b异号,则a-b的值为( B )
A.
B.
C.
5
D.
9、若a+b=0,则下列各组中不互为相反数的数是( B )
A.
和
B.
和
C.
和
D.
和
10、如果三个数的和大于0,积小于0,那么这三个数中负数有(
B
)
A.
0个
B.
1个
C.
2个
D.
3个
11、已知,则式子:(
)
A.3
B.或1
C.或3
D.1
【解析】不妨设a
<b<c.∵abc>0,∴分两种情况:
①a
<b<0<c,则=-1+(-1)+1=-1;
②a>0,b>0,c>0,则1+1+1=3.故选C.
12、如果,那么有(
A
)
A.
B.
C.
D.
二、填空题
13、仔细思考下列各对量:①胜两局与负三局;②气温升高
3℃与气温为﹣3℃;
③盈利
3
万元与支出
3
万元;④甲、乙两支球队组织了两场篮球比赛,甲、乙两
队的比分分别为
65:60
与
60:65.其中具有相反意义的量有①③
14、在一次全市的数学监测中某6名学生的成绩与全市学生的平均分80的差分别为5,﹣2,8,11,5,﹣6,则这6名学生的平均成绩为 83.5
分.
15、有六个位:0.123,(﹣1.5)3,3.1416,,﹣2π,0.1020020002…,若其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z=6.
【解答】解:无理数有:﹣2π,0.1020020002…共2个,则x=2;
没有整数:则y=0;
非负数有:0.123,3.1416,,0.1020020002…共4个;则z=4.
则x+y+z=6.
16、在﹣2、,4.121121112、π﹣3.14,、0.5中,是无理数的为 ,π﹣3.14 .
17、如图,点A,B,C为数轴上的3点,请回答下列问题:
(1)将点A向右平移3个单位长度后,点
表示的数最小;
(2)将点C向左平移6个单位长度后,点A表示的数比点C表示的数小
;
(3)将点B向左平移2个单位长度后,点B与点C的距离是
.
故答案为:(1)B;(2)1;(3)7
18、数轴上表示的数是整数的点称为整点,某数轴的单位长度是1cm,若在这个数轴上任意画出一条
长2015cm的线段AB,则线段AB盖住的整点的个数是2015或2016.
19、已知:[x]表示不超过x的最大整数.例:[4.8]=4,[-0.8]=-1.现定义:{x}=x-[x],
例:{1.5}=1.5-[1.5]=0.5,则{3.9}+{-1.8}-{1}=__0.7____.
20、a、b在的位置如图所示,则数a、-a、b、-b的大小关系为__-a<b<-b<a.____
21、已知且,那么
-2或-8
.
22、已知且,那么=
0或2
.
23、在学习了《有理数及其运算》以后,小明和小亮一起玩“24点”游戏,规则如下:从一副扑克牌(去掉大、小王)中任意抽取4张,根据牌面上的数字进行混合运算(每张牌只能用一次),使得运算结果为24或-24,其中红色扑克牌代表负数,黑色扑克牌代表正数,分别代表11、12、13.现在小亮抽到的扑克牌代表的数分别是:3、-4、-6、10,请你帮助他写一个算式,使其运算结果等于24或-24____=-24______.
24、已知光在真空中的传播速度是,1年约为,则1光年(光1年所走的路程)约为
9.45×1015
m.(用科学记数法表示)
三、解答题
25、在数轴上表示下列各数,并把它们按照从小到大的顺序排列.,,0,,
解:,,,
将各数表示在数轴上如下:
从小到大排列为:.
26、计算:
(1)(-32)+(+16)
(2)-0.5+3+2.6-5+1.15;
(3)-+-+-;
(4)(-2.5)-(+2.7)-(-1.6)-(-2.7)+(+2.4)
(5)-│4-6│-[(-2)-(-0.8)-│-2│];
(6)-32+5-3-5+12
(1)-16;(2)1;(3)-;(4)1.5
(5)2;
(6)-22
27、计算
(1);
(2);
(3)
(4)
(5)-(-
(6)(-289)÷17
【解析】(1)=
==2;
(2)===;
(3)
=
==-1;
(4)==
==0.
(5)1;
(6)-17
28、计算:
(1)
12-7×(-4)+8÷(-2)
(2)
(-42)×;
(3)
-33-(-3)2×+(-3)3÷3;
(4)
(一6)×-4×+2×;
(5)
(-2)3×[2-(-6)]+300÷5;
(6)
1-0.2×.
(7)
(8)
解:(1)36
(2)-10
(3)-33
(4)
0
(5)-4
(6)0.24
(7)
====
(8)
===35
29、阅读下面的解答过程:
计算:
观察发现,上式从第二项起,每一项都是它前一项的5倍,如果上式各项都乘5,所得新算式中除个别项外,其余与原式中的项都相同,于是两式相减将使差易于计算.
解:设①,
则②,
②-①,得
上面计算用的方法称为“错位相减法”,如果一列数,从第二项起每一项与前一项之比都相等(本例题中都等于5),那么这列数的求和问题均可用上述“错位相减法”来解决.
请你观察算式:是否具备上述规律?若具备,请你尝试“错位相减法”计算上式的结果.
()
30、某灯具厂计划一天生产300盏景观灯,但由于各种原因,实际每天生产景观灯数与计划每天生产景观灯数相比有出入.下表是某周的生产情况(增产记为正、减产记为负):
星期
一
二
三
四
五
六
日
增减
(1)求该厂本周实际生产景观灯的盏数;
(2)求产量最多的一天比产量最少的一天多生产景观灯的盏数;
(3)该厂实行每日计件工资制,每生产一盏景观灯可得60元,若超额完成任务,则超过部分每盏另奖20元,若未能完成任务,则少生产一盏扣25元,那么该厂工人这一周的工资总额是多少元?
(1)(3-5-2
+9-7+12-3
)
+
300×7=2
107(盏).
(2)产量最多的一天生产景观灯300+12=312(盏),产量最少的一天生产景观灯300-7=293(盏),
312-293=19(盏).
产量最多的一天比产量最少的一天多生产景观灯19盏
(3)
2
107×60+(3+9+12)
×20-(5+2+7+3)
×25
=
126
475(元).
该厂工人这一周的工资总额是126
475元.
一、选择题
1、下列说法中正确的是
(
)
A.有最小的正数
B.有最大的负数
C.有最小的整数
D.有最小的正整数
2、纽约、悉尼与北京时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京时间晚的时数):
城市
悉尼
纽约
时差/时
+2
-13
当北京
6
月
15
日
23
时,悉尼、纽约的时间分别是(
)
A.6
月
16
日
1
时;6
月
15
日
10
时
B.6
月
16
日
1
时;6
月
14
日
10
时
C.6
月
15
日
21
时;6
月
15
日
10
时
D.6
月
15
日
21
时;6
月
16
日
12
时
3、下列说法中,正确的是(
)
A.有理数就是正数和负数的统称
B.零不是自然数,但是正数
C.一个有理数不是整数就是分数
D.正分数、零、负分数统称分数
4、在,3.14,0,0.313
113
111.…,0.43五个数中分数有(
)个.
A.1
B.2
C.3
D.4
5、在数轴上与原点的距离等于
2
的点表示的数是(??
)
A.?2???????????????????????????????????B.?﹣2???????????????????????????????????C.?﹣1
或
3???????????????????????????????????D.?﹣2
或
2
6、如图,将一刻度尺放在数轴上.
①若刻度尺上
0cm
和
4cm
对应数轴上的点表示的数分别为
1
和
5,则
1cm
对应数轴上的点表示的数是
2;
②若刻度尺上
0cm
和
4cm
对应数轴上的点表示的数分别为
1
和
9,则
1cm
对应数轴上的点表示的数是
3;
③若刻度尺上
0cm
和
4cm
对应数轴上的点表示的数分别为-2
和
2,则
1cm
对应数轴上的点表示的数是-1;
④若刻度尺上
0cm
和
4
cm
对应数轴上的点表示的数分别为-1
和
1,则
1cm
对应数轴上的点表示的数是-0.5.
上述结论中,所有符合题意结论的序号是(??
)
A.?①②???????????????????B.?②④???????????????C.?①②③?????????????????????D.?①②③④
7、能使等式|2x﹣3|+2|x﹣2|=1成立的x的取值可以是( )
A.0
B.1
C.2
D.3
8、若a=4,|b|=3,且a,b异号,则a-b的值为( )
A.
B.
C.
5
D.
9、若a+b=0,则下列各组中不互为相反数的数是( )
A.
和
B.
和
C.
和
D.
和
10、如果三个数的和大于0,积小于0,那么这三个数中负数有(
)
A.
0个
B.
1个
C.
2个
D.
3个
11、已知,则式子:(
)
A.3
B.或1
C.或3
D.1
12、如果,那么有(
)
A.
B.
C.
D.
二、填空题
13、仔细思考下列各对量:①胜两局与负三局;②气温升高
3℃与气温为﹣3℃;
③盈利
3
万元与支出
3
万元;④甲、乙两支球队组织了两场篮球比赛,甲、乙两
队的比分分别为
65:60
与
60:65.其中具有相反意义的量有
14、在一次全市的数学监测中某6名学生的成绩与全市学生的平均分80的差分别为5,﹣2,8,11,5,﹣6,则这6名学生的平均成绩为
分.
15、有六个位:0.123,(﹣1.5)3,3.1416,,﹣2π,0.1020020002…,若其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z=______.
16、在﹣2、,4.121121112、π﹣3.14,、0.5中,是无理数的为
.
17、如图,点A,B,C为数轴上的3点,请回答下列问题:
(1)将点A向右平移3个单位长度后,点
表示的数最小;
(2)将点C向左平移6个单位长度后,点A表示的数比点C表示的数小
;
(3)将点B向左平移2个单位长度后,点B与点C的距离是
.
18、数轴上表示的数是整数的点称为整点,某数轴的单位长度是1cm,若在这个数轴上任意画出一条
长2015cm的线段AB,则线段AB盖住的整点的个数是
.
19、已知:[x]表示不超过x的最大整数.例:[4.8]=4,[-0.8]=-1.现定义:{x}=x-[x],
例:{1.5}=1.5-[1.5]=0.5,则{3.9}+{-1.8}-{1}=______.
20、a、b在的位置如图所示,则数a、-a、b、-b的大小关系为______
21、已知且,那么
.
22、已知且,那么=
.
23、在学习了《有理数及其运算》以后,小明和小亮一起玩“24点”游戏,规则如下:从一副扑克牌(去掉大、小王)中任意抽取4张,根据牌面上的数字进行混合运算(每张牌只能用一次),使得运算结果为24或-24,其中红色扑克牌代表负数,黑色扑克牌代表正数,分别代表11、12、13.现在小亮抽到的扑克牌代表的数分别是:3、-4、-6、10,请你帮助他写一个算式,使其运算结果等于24或-24__________.
24、已知光在真空中的传播速度是,1年约为,则1光年(光1年所走的路程)约为
m.(用科学记数法表示)
三、解答题
25、在数轴上表示下列各数,并把它们按照从小到大的顺序排列.,,0,,
26、计算:
(1)(-32)+(+16)
(2)-0.5+3+2.6-5+1.15;
(3)-+-+-;
(4)(-2.5)-(+2.7)-(-1.6)-(-2.7)+(+2.4)
(5)-│4-6│-[(-2)-(-0.8)-│-2│];
(6)-32+5-3-5+12
27、计算
(1);
(2);
(3)
(4)
(5)-(-
(6)(-289)÷17
28、计算:
(1)
12-7×(-4)+8÷(-2)
(2)
(-42)×;
(3)
-33-(-3)2×+(-3)3÷3;
(4)
(一6)×-4×+2×;
(5)
(-2)3×[2-(-6)]+300÷5;
(6)
1-0.2×.
(7)
(8)
29、阅读下面的解答过程:
计算:
观察发现,上式从第二项起,每一项都是它前一项的5倍,如果上式各项都乘5,所得新算式中除个别项外,其余与原式中的项都相同,于是两式相减将使差易于计算.
解:设①,
则②,
②-①,得
上面计算用的方法称为“错位相减法”,如果一列数,从第二项起每一项与前一项之比都相等(本例题中都等于5),那么这列数的求和问题均可用上述“错位相减法”来解决.
请你观察算式:是否具备上述规律?若具备,请你尝试“错位相减法”计算上式的结果.
30、某灯具厂计划一天生产300盏景观灯,但由于各种原因,实际每天生产景观灯数与计划每天生产景观灯数相比有出入.下表是某周的生产情况(增产记为正、减产记为负):
星期
一
二
三
四
五
六
日
增减
(1)求该厂本周实际生产景观灯的盏数;
(2)求产量最多的一天比产量最少的一天多生产景观灯的盏数;
(3)该厂实行每日计件工资制,每生产一盏景观灯可得60元,若超额完成任务,则超过部分每盏另奖20元,若未能完成任务,则少生产一盏扣25元,那么该厂工人这一周的工资总额是多少元?
2020-2021苏科版七年级数学上册第2章有理数章末培优训练卷(答案)
一、选择题
1、下列说法中正确的是
(
D
)
A.有最小的正数
B.有最大的负数
C.有最小的整数
D.有最小的正整数
2、纽约、悉尼与北京时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京时间晚的时数):
城市
悉尼
纽约
时差/时
+2
-13
当北京
6
月
15
日
23
时,悉尼、纽约的时间分别是(A
)
A.6
月
16
日
1
时;6
月
15
日
10
时
B.6
月
16
日
1
时;6
月
14
日
10
时
C.6
月
15
日
21
时;6
月
15
日
10
时
D.6
月
15
日
21
时;6
月
16
日
12
时
3、下列说法中,正确的是(
C
)
A.有理数就是正数和负数的统称
B.零不是自然数,但是正数
C.一个有理数不是整数就是分数
D.正分数、零、负分数统称分数
4、在,3.14,0,0.313
113
111.…,0.43五个数中分数有(
B
)个.
A.1
B.2
C.3
D.4
5、在数轴上与原点的距离等于
2
的点表示的数是(??D
)
A.?2???????????????????????????????????B.?﹣2???????????????????????????????????C.?﹣1
或
3???????????????????????????????????D.?﹣2
或
2
6、如图,将一刻度尺放在数轴上.
①若刻度尺上
0cm
和
4cm
对应数轴上的点表示的数分别为
1
和
5,则
1cm
对应数轴上的点表示的数是
2;
②若刻度尺上
0cm
和
4cm
对应数轴上的点表示的数分别为
1
和
9,则
1cm
对应数轴上的点表示的数是
3;
③若刻度尺上
0cm
和
4cm
对应数轴上的点表示的数分别为-2
和
2,则
1cm
对应数轴上的点表示的数是-1;
④若刻度尺上
0cm
和
4
cm
对应数轴上的点表示的数分别为-1
和
1,则
1cm
对应数轴上的点表示的数是-0.5.
上述结论中,所有符合题意结论的序号是(??D
)
A.?①②???????????????????B.?②④???????????????C.?①②③?????????????????????D.?①②③④
7、能使等式|2x﹣3|+2|x﹣2|=1成立的x的取值可以是( )
A.0
B.1
C.2
D.3
【分析】直接利用绝对值的性质把x的值分别代入求出答案.
【解析】A、当x=0时,原式=3+4=7,不合题意;
B、当x=1时,原式=1+2=3,不合题意;
C、当x=2时,原式=1+0=1,符合题意;
D、当x=3时,原式=3+2=5,不合题意;
故选:C.
8、若a=4,|b|=3,且a,b异号,则a-b的值为( B )
A.
B.
C.
5
D.
9、若a+b=0,则下列各组中不互为相反数的数是( B )
A.
和
B.
和
C.
和
D.
和
10、如果三个数的和大于0,积小于0,那么这三个数中负数有(
B
)
A.
0个
B.
1个
C.
2个
D.
3个
11、已知,则式子:(
)
A.3
B.或1
C.或3
D.1
【解析】不妨设a
<b<c.∵abc>0,∴分两种情况:
①a
<b<0<c,则=-1+(-1)+1=-1;
②a>0,b>0,c>0,则1+1+1=3.故选C.
12、如果,那么有(
A
)
A.
B.
C.
D.
二、填空题
13、仔细思考下列各对量:①胜两局与负三局;②气温升高
3℃与气温为﹣3℃;
③盈利
3
万元与支出
3
万元;④甲、乙两支球队组织了两场篮球比赛,甲、乙两
队的比分分别为
65:60
与
60:65.其中具有相反意义的量有①③
14、在一次全市的数学监测中某6名学生的成绩与全市学生的平均分80的差分别为5,﹣2,8,11,5,﹣6,则这6名学生的平均成绩为 83.5
分.
15、有六个位:0.123,(﹣1.5)3,3.1416,,﹣2π,0.1020020002…,若其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z=6.
【解答】解:无理数有:﹣2π,0.1020020002…共2个,则x=2;
没有整数:则y=0;
非负数有:0.123,3.1416,,0.1020020002…共4个;则z=4.
则x+y+z=6.
16、在﹣2、,4.121121112、π﹣3.14,、0.5中,是无理数的为 ,π﹣3.14 .
17、如图,点A,B,C为数轴上的3点,请回答下列问题:
(1)将点A向右平移3个单位长度后,点
表示的数最小;
(2)将点C向左平移6个单位长度后,点A表示的数比点C表示的数小
;
(3)将点B向左平移2个单位长度后,点B与点C的距离是
.
故答案为:(1)B;(2)1;(3)7
18、数轴上表示的数是整数的点称为整点,某数轴的单位长度是1cm,若在这个数轴上任意画出一条
长2015cm的线段AB,则线段AB盖住的整点的个数是2015或2016.
19、已知:[x]表示不超过x的最大整数.例:[4.8]=4,[-0.8]=-1.现定义:{x}=x-[x],
例:{1.5}=1.5-[1.5]=0.5,则{3.9}+{-1.8}-{1}=__0.7____.
20、a、b在的位置如图所示,则数a、-a、b、-b的大小关系为__-a<b<-b<a.____
21、已知且,那么
-2或-8
.
22、已知且,那么=
0或2
.
23、在学习了《有理数及其运算》以后,小明和小亮一起玩“24点”游戏,规则如下:从一副扑克牌(去掉大、小王)中任意抽取4张,根据牌面上的数字进行混合运算(每张牌只能用一次),使得运算结果为24或-24,其中红色扑克牌代表负数,黑色扑克牌代表正数,分别代表11、12、13.现在小亮抽到的扑克牌代表的数分别是:3、-4、-6、10,请你帮助他写一个算式,使其运算结果等于24或-24____=-24______.
24、已知光在真空中的传播速度是,1年约为,则1光年(光1年所走的路程)约为
9.45×1015
m.(用科学记数法表示)
三、解答题
25、在数轴上表示下列各数,并把它们按照从小到大的顺序排列.,,0,,
解:,,,
将各数表示在数轴上如下:
从小到大排列为:.
26、计算:
(1)(-32)+(+16)
(2)-0.5+3+2.6-5+1.15;
(3)-+-+-;
(4)(-2.5)-(+2.7)-(-1.6)-(-2.7)+(+2.4)
(5)-│4-6│-[(-2)-(-0.8)-│-2│];
(6)-32+5-3-5+12
(1)-16;(2)1;(3)-;(4)1.5
(5)2;
(6)-22
27、计算
(1);
(2);
(3)
(4)
(5)-(-
(6)(-289)÷17
【解析】(1)=
==2;
(2)===;
(3)
=
==-1;
(4)==
==0.
(5)1;
(6)-17
28、计算:
(1)
12-7×(-4)+8÷(-2)
(2)
(-42)×;
(3)
-33-(-3)2×+(-3)3÷3;
(4)
(一6)×-4×+2×;
(5)
(-2)3×[2-(-6)]+300÷5;
(6)
1-0.2×.
(7)
(8)
解:(1)36
(2)-10
(3)-33
(4)
0
(5)-4
(6)0.24
(7)
====
(8)
===35
29、阅读下面的解答过程:
计算:
观察发现,上式从第二项起,每一项都是它前一项的5倍,如果上式各项都乘5,所得新算式中除个别项外,其余与原式中的项都相同,于是两式相减将使差易于计算.
解:设①,
则②,
②-①,得
上面计算用的方法称为“错位相减法”,如果一列数,从第二项起每一项与前一项之比都相等(本例题中都等于5),那么这列数的求和问题均可用上述“错位相减法”来解决.
请你观察算式:是否具备上述规律?若具备,请你尝试“错位相减法”计算上式的结果.
()
30、某灯具厂计划一天生产300盏景观灯,但由于各种原因,实际每天生产景观灯数与计划每天生产景观灯数相比有出入.下表是某周的生产情况(增产记为正、减产记为负):
星期
一
二
三
四
五
六
日
增减
(1)求该厂本周实际生产景观灯的盏数;
(2)求产量最多的一天比产量最少的一天多生产景观灯的盏数;
(3)该厂实行每日计件工资制,每生产一盏景观灯可得60元,若超额完成任务,则超过部分每盏另奖20元,若未能完成任务,则少生产一盏扣25元,那么该厂工人这一周的工资总额是多少元?
(1)(3-5-2
+9-7+12-3
)
+
300×7=2
107(盏).
(2)产量最多的一天生产景观灯300+12=312(盏),产量最少的一天生产景观灯300-7=293(盏),
312-293=19(盏).
产量最多的一天比产量最少的一天多生产景观灯19盏
(3)
2
107×60+(3+9+12)
×20-(5+2+7+3)
×25
=
126
475(元).
该厂工人这一周的工资总额是126
475元.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
