沪科版数学八年级上册:13.2命题的证明 教案(表格式)
文档属性
| 名称 | 沪科版数学八年级上册:13.2命题的证明 教案(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 56.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 09:27:50 | ||
图片预览

文档简介
教学设计方案
课题名称
三角形的外角
姓名
工作单位
年级学科
8年级数学
教材版本
沪科版
教学目标
知识与技能:?了解三角形的外角概念,掌握三角形外角的性质,初步学会数学说理,能利用三角形的外角性质解决简单的实际问题
过程与方法:通过小组学习、动手操作、探索发现等活动经历培养学生比较、猜想、类比、转化的思想方法。初步学会建立数学模型、运用简单的说理来计算三角形相关的角。
情感态度与价值:通过观察和动手操作,体会探索过程,学会推理的数学思想方法,培养主动探索、勇于发现,敢于实践及合作交流的习惯。
教学重点
掌握三角形外角的二个性质,学会简单推理。
教学难点
类比三角形内角和的证明方法来证明三角形外角性质?,初步学会数学说理。注重渗透数学说理过程,从简单的问题中逐步培养学生运用几何语言的能力。?
教学过程设计
问题与情景
师生行为
设计意图
复
习
引
入
活动一:
回顾复习,
投影显示课题。
师:我们前面已经学习过了三角形的内角知识,我们一起来回顾下:
1、三角形内角的定义
三角形相邻两边组成的角,叫三角形的内角
2、三角形内角的性质
三角形三个内角的和为1800
投影图片,学生观察
师:为解决传球问题,引出外角的概念。
熟悉一遍已经学过的知识,为新知识载入打下基础
通过一个成语合理导入外角。
交
流
探索
合
作
交
流
探
索
新
知
活动二:
让学生归纳出三角形外角的定义。
学生描述,老师总结.
投影出三角形外角的定义。
三角形的一条边与另一条边的延长线所形成的夹角叫三角形的外角。
让学生自己通过画图、观察、归纳,总结出三角形外角的特征,自己得出三角形外角的定义
活动三:
投影出示问题,让学生回答,及时巩固所学概念。
自主交流,探讨外角应该知会的内容,确定学习目标。
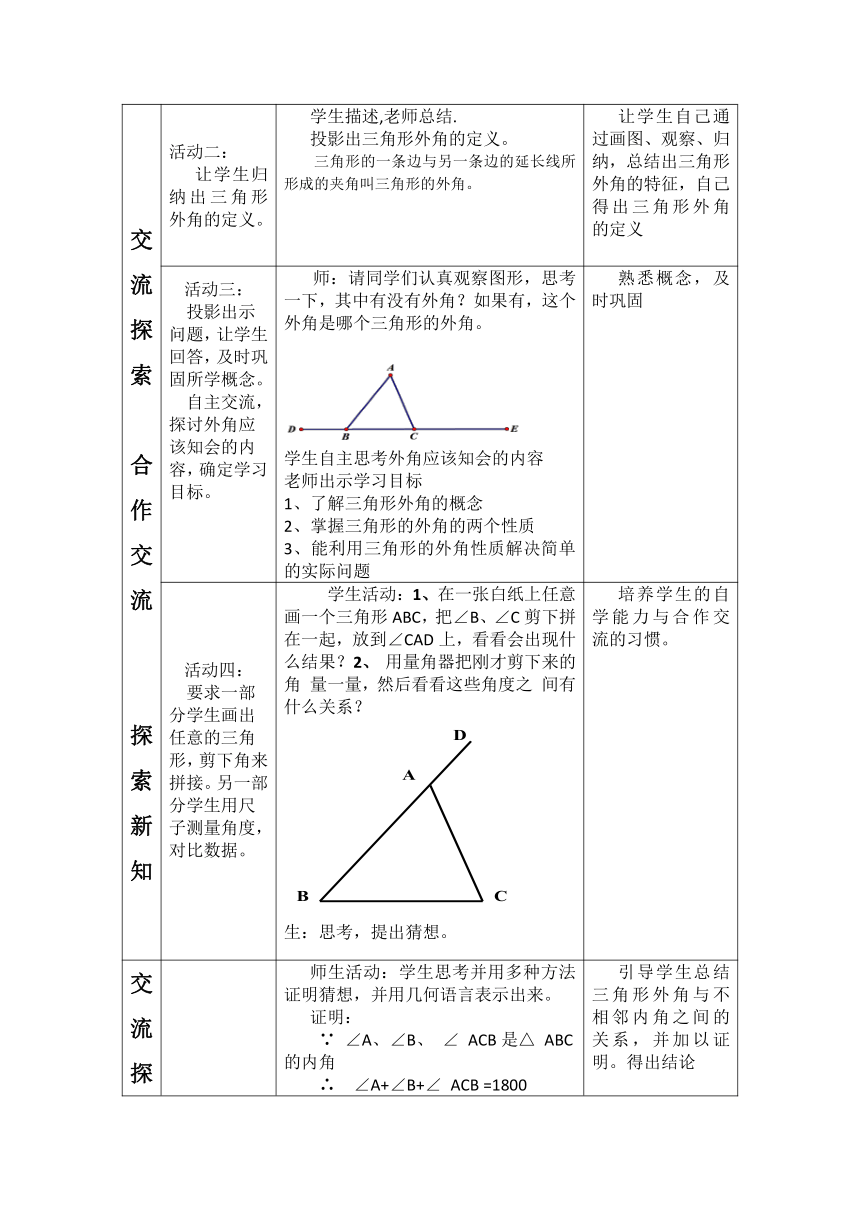
师:请同学们认真观察图形,思考一下,其中有没有外角?如果有,这个外角是哪个三角形的外角。
学生自主思考外角应该知会的内容
老师出示学习目标
1、了解三角形外角的概念
2、掌握三角形的外角的两个性质
3、能利用三角形的外角性质解决简单的实际问题
熟悉概念,及时巩固
活动四:
要求一部分学生画出任意的三角形,剪下角来拼接。另一部分学生用尺子测量角度,对比数据。
学生活动:1、在一张白纸上任意画一个三角形ABC,把∠B、∠C剪下拼在一起,放到∠CAD上,看看会出现什么结果?2、
用量角器把刚才剪下来的角
量一量,然后看看这些角度之
间有什么关系?
生:思考,提出猜想。
培养学生的自学能力与合作交流的习惯。
交流探索
师生活动:学生思考并用多种方法证明猜想,并用几何语言表示出来。
证明:
∵
∠A、∠B、
∠
ACB是△
ABC的内角
∴
∠A+∠B+∠
ACB
=1800
又∵
∠ACD+∠
ACB
=1800
∴
∠
A+∠B=
∠ACD
师生活动:学生交流,师生共同总结:
三角形的一个外角等于与它不相邻的两个内角之和。
同时得到:
三角形的一个外角大于与它不相邻的任何一个内角
引导学生总结三角形外角与不相邻内角之间的关系,并加以证明。得出结论
巩固练习强化新知
活动五:
巩固练习
(1)求下列各图中∠α的度数
(2)判断题
1、三角形的外角等于任意两个内角的和。(
)
2、三角形的一个外角大于任何一个内角。(
)
(3)判断∠1与∠3的大小,并说明理由。
解:∠3
>∠1,理由如下:
如图∵
∠3是△
ADE的一个外角
∴
∠3
>
∠2
∵
∠2是△
ABC的一个外角
∴
∠2
>
∠1
∴∠3
>∠1
(4)如图,计算∠BOC的度数
解:连接BO并交AC于点D
∵
∠ODC是△
ADB的一个外角
∴
∠ODC=∠
B
+∠A
∵
∠BOC是△
DOC的一个外角
∴
∠BOC
=
∠
C+∠ODC
∴∠BOC=∠B+∠C+
∠A
=250+450+300
=1000
(5)在△
ABC中,AD、BE、CF分别为
三角形三边的延长线。
求∠1+
∠2+
∠3
通过练习,反馈,了解学生对新知的掌握。教师的指导可以提升学生对知识的理解。
总结新知
活动六:
课堂小结
1、三角形外角的定义
三角形一边与另一边的延长线所形成的夹角
2、三角形外角的性质
(1):三角形的外角等于和它不相邻的两个内角之和
(2):三角形的外角大于与它不相邻的任何一个内角
3、小旗模型和镖行模型
梳理本节知识,在交流中加深对本节课重点知识的理解。
作业设置
活动七:
布置作业
作业:
教材83页1、2题
教材85页第9题
巩固所学知识,使学生得到发展。
板书设计
三角形外角的性质
定义:
三角形的一边与另一边的延长线所组成的角,叫做三角形的外角。
推论3
三角形的外角等于与它不相邻的两个内角的和。
推论4
三角形的外角大于与它不相邻的任何一个内角。
教学设计说明
本节课给学生留有充足的探索空间,让学生经历“感知——操作——归纳——验证——应用”的完整学习过程。
两个数学模型的建立,让学生?团队合作能力,分析问题的能力,处理数据的能力都得到了锻炼。
课题名称
三角形的外角
姓名
工作单位
年级学科
8年级数学
教材版本
沪科版
教学目标
知识与技能:?了解三角形的外角概念,掌握三角形外角的性质,初步学会数学说理,能利用三角形的外角性质解决简单的实际问题
过程与方法:通过小组学习、动手操作、探索发现等活动经历培养学生比较、猜想、类比、转化的思想方法。初步学会建立数学模型、运用简单的说理来计算三角形相关的角。
情感态度与价值:通过观察和动手操作,体会探索过程,学会推理的数学思想方法,培养主动探索、勇于发现,敢于实践及合作交流的习惯。
教学重点
掌握三角形外角的二个性质,学会简单推理。
教学难点
类比三角形内角和的证明方法来证明三角形外角性质?,初步学会数学说理。注重渗透数学说理过程,从简单的问题中逐步培养学生运用几何语言的能力。?
教学过程设计
问题与情景
师生行为
设计意图
复
习
引
入
活动一:
回顾复习,
投影显示课题。
师:我们前面已经学习过了三角形的内角知识,我们一起来回顾下:
1、三角形内角的定义
三角形相邻两边组成的角,叫三角形的内角
2、三角形内角的性质
三角形三个内角的和为1800
投影图片,学生观察
师:为解决传球问题,引出外角的概念。
熟悉一遍已经学过的知识,为新知识载入打下基础
通过一个成语合理导入外角。
交
流
探索
合
作
交
流
探
索
新
知
活动二:
让学生归纳出三角形外角的定义。
学生描述,老师总结.
投影出三角形外角的定义。
三角形的一条边与另一条边的延长线所形成的夹角叫三角形的外角。
让学生自己通过画图、观察、归纳,总结出三角形外角的特征,自己得出三角形外角的定义
活动三:
投影出示问题,让学生回答,及时巩固所学概念。
自主交流,探讨外角应该知会的内容,确定学习目标。
师:请同学们认真观察图形,思考一下,其中有没有外角?如果有,这个外角是哪个三角形的外角。
学生自主思考外角应该知会的内容
老师出示学习目标
1、了解三角形外角的概念
2、掌握三角形的外角的两个性质
3、能利用三角形的外角性质解决简单的实际问题
熟悉概念,及时巩固
活动四:
要求一部分学生画出任意的三角形,剪下角来拼接。另一部分学生用尺子测量角度,对比数据。
学生活动:1、在一张白纸上任意画一个三角形ABC,把∠B、∠C剪下拼在一起,放到∠CAD上,看看会出现什么结果?2、
用量角器把刚才剪下来的角
量一量,然后看看这些角度之
间有什么关系?
生:思考,提出猜想。
培养学生的自学能力与合作交流的习惯。
交流探索
师生活动:学生思考并用多种方法证明猜想,并用几何语言表示出来。
证明:
∵
∠A、∠B、
∠
ACB是△
ABC的内角
∴
∠A+∠B+∠
ACB
=1800
又∵
∠ACD+∠
ACB
=1800
∴
∠
A+∠B=
∠ACD
师生活动:学生交流,师生共同总结:
三角形的一个外角等于与它不相邻的两个内角之和。
同时得到:
三角形的一个外角大于与它不相邻的任何一个内角
引导学生总结三角形外角与不相邻内角之间的关系,并加以证明。得出结论
巩固练习强化新知
活动五:
巩固练习
(1)求下列各图中∠α的度数
(2)判断题
1、三角形的外角等于任意两个内角的和。(
)
2、三角形的一个外角大于任何一个内角。(
)
(3)判断∠1与∠3的大小,并说明理由。
解:∠3
>∠1,理由如下:
如图∵
∠3是△
ADE的一个外角
∴
∠3
>
∠2
∵
∠2是△
ABC的一个外角
∴
∠2
>
∠1
∴∠3
>∠1
(4)如图,计算∠BOC的度数
解:连接BO并交AC于点D
∵
∠ODC是△
ADB的一个外角
∴
∠ODC=∠
B
+∠A
∵
∠BOC是△
DOC的一个外角
∴
∠BOC
=
∠
C+∠ODC
∴∠BOC=∠B+∠C+
∠A
=250+450+300
=1000
(5)在△
ABC中,AD、BE、CF分别为
三角形三边的延长线。
求∠1+
∠2+
∠3
通过练习,反馈,了解学生对新知的掌握。教师的指导可以提升学生对知识的理解。
总结新知
活动六:
课堂小结
1、三角形外角的定义
三角形一边与另一边的延长线所形成的夹角
2、三角形外角的性质
(1):三角形的外角等于和它不相邻的两个内角之和
(2):三角形的外角大于与它不相邻的任何一个内角
3、小旗模型和镖行模型
梳理本节知识,在交流中加深对本节课重点知识的理解。
作业设置
活动七:
布置作业
作业:
教材83页1、2题
教材85页第9题
巩固所学知识,使学生得到发展。
板书设计
三角形外角的性质
定义:
三角形的一边与另一边的延长线所组成的角,叫做三角形的外角。
推论3
三角形的外角等于与它不相邻的两个内角的和。
推论4
三角形的外角大于与它不相邻的任何一个内角。
教学设计说明
本节课给学生留有充足的探索空间,让学生经历“感知——操作——归纳——验证——应用”的完整学习过程。
两个数学模型的建立,让学生?团队合作能力,分析问题的能力,处理数据的能力都得到了锻炼。
