北师大版数学九年级上册1.3 正方形的性质与判定(第1课时 正方形的性质》课件(共26张)
文档属性
| 名称 | 北师大版数学九年级上册1.3 正方形的性质与判定(第1课时 正方形的性质》课件(共26张) |  | |
| 格式 | zip | ||
| 文件大小 | 540.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 09:44:06 | ||
图片预览






文档简介
(共28张PPT)
北师大版数学九年级上册
第一章
特殊的平行四边形
1.3
正方形的性质与判定
第1课时
正方形的性质
1.掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系.
2.掌握正方形的性质,能正确运用正方形的性质解题.
学习目标
1.菱形的四条边都______,菱形的对角线__________
.
2.矩形的四个角都是______
,矩形的对角线______
3.有一组邻边相等的平行四边形叫______;有一个角是直角的平行四边形叫做______.
相等
互相垂直
直角
相等.
菱形
矩形
回顾旧知
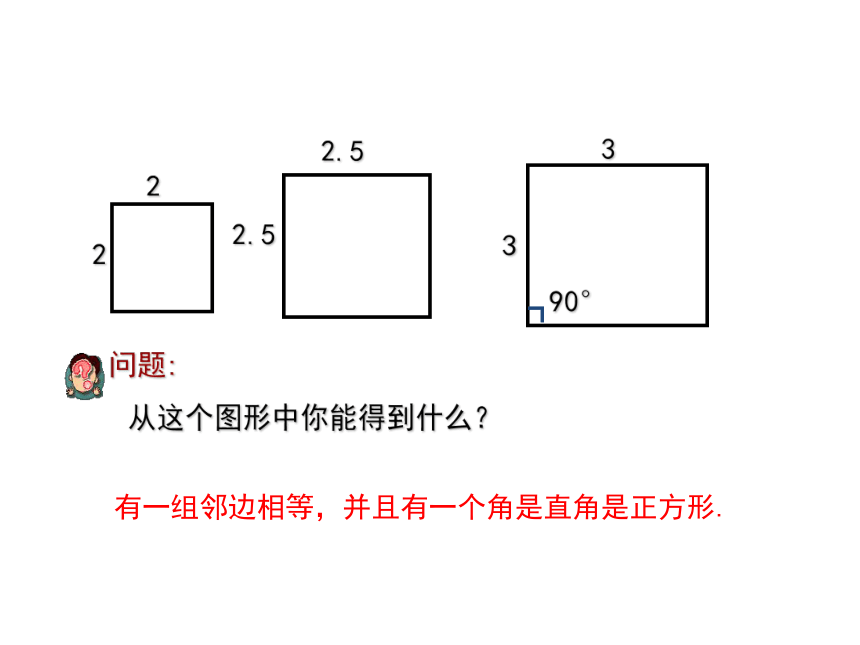
问题:
从这个图形中你能得到什么?
┓
90°
有一组邻边相等,并且有一个角是直角是正方形.
2.5
2.5
3
3
2
2
知识模块一 探索正方形的性质
(一)自主探究
1.正方形的定义是什么?
答:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
2.正方形是矩形吗?是菱形吗?
答:正方形是特殊的矩形,也是特殊的菱形.
探究新知
(二)合作探究
1.在我们的生活中除了矩形、菱形外,还有什么特殊的平行四边形呢?
菱形
矩形
正方形
2.展示正方形图片,让学生观察它们有什么共同特征.
归纳结论:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
3.做一做:用一张长方形的纸片折出一个正方形.
4.观察:正方形具有哪些性质?
归纳结论:正方形的四个角都是直角,四条边相等.正方形的对角线相等且互相垂直平分.
5.议一议:平行四边形、菱形、矩形、正方形之间有什么关系?你能用一个图直观地说明吗?
答:如图:
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
性质:1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
知识模块二 正方形的性质应用
(一)自主探究
1.正方形具有而矩形不具有的性质是(
)
A.四个角都是直角
B.一条对角线平分一组对角
C.对角线相等
D.对边互相平行
2.下列性质,正方形具有而菱形不具有的性质是__________
(填序号)
①四边相等;②对角线互相平分;③对角线相等;④对角线互相垂直;⑤四个角都是直角;⑥每一条对角线平分一组对角;⑦有4条对称轴.
B
③⑤⑦
(二)合作探究
例
如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,求∠EAF的度数.
分析:根据直角三角形全等的判定定理,可得出△ABF≌△AGF,故有∠BAF=∠GAF,再证明△AGE≌△ADE,有∠GAE=∠DAE,所以可得∠EAF=45°.
解:在Rt△ABF与Rt△AGF中,
∵AB=AG,AF=AF,∠B=∠AGF=90°,∴△ABF≌△AGF(HL),∴∠BAF=∠GAF,
同理易得:△AGE≌△ADE,有∠GAE=∠DAE;
即∠EAF=∠EAG+∠FAG=
(∠DAG+∠BAG)=
∠DAB=45°
故∠EAF=45°.
练习
如图:四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心_____点,按顺时针方向旋转_____
度得到;
(3)若BC=8,DE=6,求△AEF的面积.
解:(1)由SAS证明△ADE≌△ABF;
(3)由勾股定理得AE=10,
由(1)得AE=AF,∠DAE=∠BAF,
进而证∠EAF=90°,
∴△AEF的面积=
AE2=
×100=50.
A
90
1.如图,P是正方形ABCD的对角线BD上一点,PM⊥AD于M,PN⊥AB于N,若AB=4,则四边形ANPM的周长等于(
)
A.4 B.8 C.4 D.8
2.如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=1,CF=3,则AB的长度为_____.
B
巩固练习
3.如图所示,在正方形ABCD中,M是BC上一点,连接AM,作AM的垂线GH交AB于G,交CD于H,若AM=10cm,则GH=____cm
10
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形.
总结新知
1.正方形是轴对称图形,它的对称轴共有(
)
A.1条
B.2条
C.3条
D.4条
D
课堂练习
2.平行四边形、矩形、菱形、正方形都具有的性质是(
)
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
A
3.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为1和2,则正方形的边长是_____.
4.如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1,以点A为中心,把△ADE顺时针旋转90°,得△ABE′,连接EE′,则EE′的长等于_______.
2
5.如图,A、B、C三点在同一条直线上,AB=2BC,分别以AB、BC为边作正方形ABEF和正方形BCMN,连接FN、EC.
求证:FN=EC.
解:
∵四边形ABEF、BCMN为正方形,∴AB=BE=EF,BC=BN,∠FEB=∠EBC=90°,∵AB=2BC,∴BE=2BN,∴EN=NB=BC,∴在△FEN和△EBC中
,∴△FEN≌△EBC(SAS),∴FN=EC.
6.如图,并排摆放两个正方形ABCD和FEBG,其中正方形FEBG的边长为3cm,则图中阴影部分的面积是多少?
解:设正方形ABCD的边长为a,则S阴影部分=S△EBG+S梯形GBCD-S△ECD=
×3×3+
(3+a)a-
(3+a)a=
(cm2).
7.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,
求∠EGC的大小.
解:(1)∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵BE⊥BF,
∴∠FBE=90°,
∵∠ABE+∠EBC=90°,∠CBF+∠EBC=90°,
∴∠ABE=∠CBF,
∵BE=BF,
∴△AEB≌△CFB(SAS),
∴AE=CF;
(2)
80°
再
见
北师大版数学九年级上册
第一章
特殊的平行四边形
1.3
正方形的性质与判定
第1课时
正方形的性质
1.掌握正方形的定义,弄清正方形与平行四边形、菱形、矩形的关系.
2.掌握正方形的性质,能正确运用正方形的性质解题.
学习目标
1.菱形的四条边都______,菱形的对角线__________
.
2.矩形的四个角都是______
,矩形的对角线______
3.有一组邻边相等的平行四边形叫______;有一个角是直角的平行四边形叫做______.
相等
互相垂直
直角
相等.
菱形
矩形
回顾旧知
问题:
从这个图形中你能得到什么?
┓
90°
有一组邻边相等,并且有一个角是直角是正方形.
2.5
2.5
3
3
2
2
知识模块一 探索正方形的性质
(一)自主探究
1.正方形的定义是什么?
答:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
2.正方形是矩形吗?是菱形吗?
答:正方形是特殊的矩形,也是特殊的菱形.
探究新知
(二)合作探究
1.在我们的生活中除了矩形、菱形外,还有什么特殊的平行四边形呢?
菱形
矩形
正方形
2.展示正方形图片,让学生观察它们有什么共同特征.
归纳结论:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
3.做一做:用一张长方形的纸片折出一个正方形.
4.观察:正方形具有哪些性质?
归纳结论:正方形的四个角都是直角,四条边相等.正方形的对角线相等且互相垂直平分.
5.议一议:平行四边形、菱形、矩形、正方形之间有什么关系?你能用一个图直观地说明吗?
答:如图:
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
性质:1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
知识模块二 正方形的性质应用
(一)自主探究
1.正方形具有而矩形不具有的性质是(
)
A.四个角都是直角
B.一条对角线平分一组对角
C.对角线相等
D.对边互相平行
2.下列性质,正方形具有而菱形不具有的性质是__________
(填序号)
①四边相等;②对角线互相平分;③对角线相等;④对角线互相垂直;⑤四个角都是直角;⑥每一条对角线平分一组对角;⑦有4条对称轴.
B
③⑤⑦
(二)合作探究
例
如图,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF,垂足为G,且AG=AB,求∠EAF的度数.
分析:根据直角三角形全等的判定定理,可得出△ABF≌△AGF,故有∠BAF=∠GAF,再证明△AGE≌△ADE,有∠GAE=∠DAE,所以可得∠EAF=45°.
解:在Rt△ABF与Rt△AGF中,
∵AB=AG,AF=AF,∠B=∠AGF=90°,∴△ABF≌△AGF(HL),∴∠BAF=∠GAF,
同理易得:△AGE≌△ADE,有∠GAE=∠DAE;
即∠EAF=∠EAG+∠FAG=
(∠DAG+∠BAG)=
∠DAB=45°
故∠EAF=45°.
练习
如图:四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心_____点,按顺时针方向旋转_____
度得到;
(3)若BC=8,DE=6,求△AEF的面积.
解:(1)由SAS证明△ADE≌△ABF;
(3)由勾股定理得AE=10,
由(1)得AE=AF,∠DAE=∠BAF,
进而证∠EAF=90°,
∴△AEF的面积=
AE2=
×100=50.
A
90
1.如图,P是正方形ABCD的对角线BD上一点,PM⊥AD于M,PN⊥AB于N,若AB=4,则四边形ANPM的周长等于(
)
A.4 B.8 C.4 D.8
2.如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=1,CF=3,则AB的长度为_____.
B
巩固练习
3.如图所示,在正方形ABCD中,M是BC上一点,连接AM,作AM的垂线GH交AB于G,交CD于H,若AM=10cm,则GH=____cm
10
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形.
总结新知
1.正方形是轴对称图形,它的对称轴共有(
)
A.1条
B.2条
C.3条
D.4条
D
课堂练习
2.平行四边形、矩形、菱形、正方形都具有的性质是(
)
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
A
3.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为1和2,则正方形的边长是_____.
4.如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1,以点A为中心,把△ADE顺时针旋转90°,得△ABE′,连接EE′,则EE′的长等于_______.
2
5.如图,A、B、C三点在同一条直线上,AB=2BC,分别以AB、BC为边作正方形ABEF和正方形BCMN,连接FN、EC.
求证:FN=EC.
解:
∵四边形ABEF、BCMN为正方形,∴AB=BE=EF,BC=BN,∠FEB=∠EBC=90°,∵AB=2BC,∴BE=2BN,∴EN=NB=BC,∴在△FEN和△EBC中
,∴△FEN≌△EBC(SAS),∴FN=EC.
6.如图,并排摆放两个正方形ABCD和FEBG,其中正方形FEBG的边长为3cm,则图中阴影部分的面积是多少?
解:设正方形ABCD的边长为a,则S阴影部分=S△EBG+S梯形GBCD-S△ECD=
×3×3+
(3+a)a-
(3+a)a=
(cm2).
7.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,
求∠EGC的大小.
解:(1)∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵BE⊥BF,
∴∠FBE=90°,
∵∠ABE+∠EBC=90°,∠CBF+∠EBC=90°,
∴∠ABE=∠CBF,
∵BE=BF,
∴△AEB≌△CFB(SAS),
∴AE=CF;
(2)
80°
再
见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
