1.1数据及其特征 课件(47张幻灯片)
文档属性
| 名称 | 1.1数据及其特征 课件(47张幻灯片) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览











文档简介
(共47张PPT)
数据与计算
信息技术必修1
第一章
数据与信息
数据
什么是数据呢?其实数据就在我们身边。
在日常生活中,人们常用符号来表达客观事物。例如:180cm、70kg、36.5℃可以分别代表人的身高、体重、体温情况;200㎡、600m?、120km/h可以分别表示物体的面积、体积、速度情况,都是数据。
数据可以用来描述不同事物的特征。
数据可用于描述事物。
数据是信息的载体。
1.1数据及其特征
数据
数据是现实世界客观事物的符号记录,是信息的载体,是计算机加工的对象。
在计算机科学中,数据是对所有输入计算机并被计算机识别、存储和处理的符号的总称,是联系现实世界和计算机世界的途径。
生活中的各种符号
现实世界中的各种符号
包括图形、图像、视频、音频、文本(文字、数字、数值、字符)等数值型和非数值型符号。
各种现实世界中的符号都可以被计算机转化为二进制数,进行各种逻辑运算,处理成有意义的数据;然后将计算机运算的二进制数转换成现实世界的视、听、触等各种感觉的信息。
如:
180cm在计算机中转换成二进制:“180”在计算机中表示为10110100;字符“cm”在计算机中表示为0110001101101101;合在一起变为“10110100
0110001101101101”
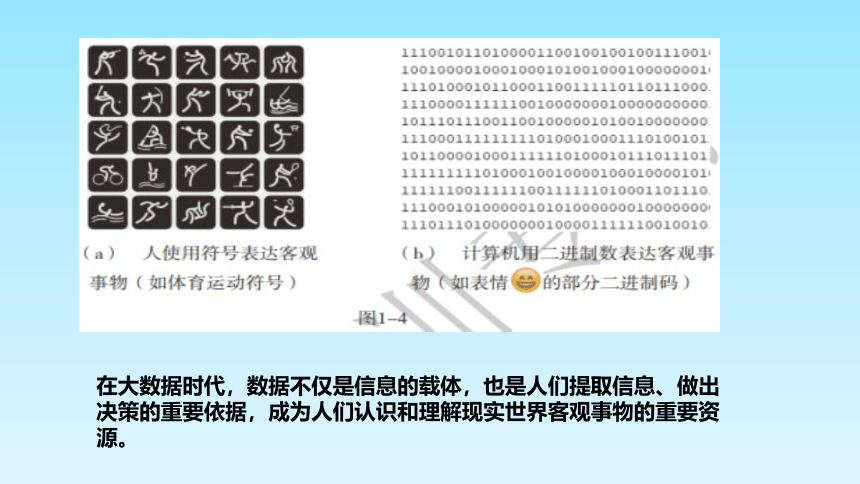
在大数据时代,数据不仅是信息的载体,也是人们提取信息、做出决策的重要依据,成为人们认识和理解现实世界客观事物的重要资源。
数据的基本特征
二进制。在计算机中,数据以二进制的形式存储、加工。
语义性。语义是将数据符号解释为客观世界的事物。
分散性。数据是分散的记录,分别记录不同客观事物的运动状态。
多样性和感知性。数据记录的形式是多样的、可看的、可听的、可感知的,如图形、图像、视频、音频、文本等。
课堂练习
1.人们用数据记录自然现象与社会发展,数据可以用来描述不同事物的特征。(
)
2.数据是现实世界客观事物的符号记录,是信息的载体,不能用计算机进行加工。(
)
3.以下关于数据的说法正确的是(
)
A.
数据是计算机被发明之后产生的,所以在古代没有数据。
B.
数据的记录过程一定需要人的参与。
C.
数据就是信息,信息就是数据。
D.
数据在人们的生活中正扮演着越来越重要的作用。
对
错
D
我们日常生活中最常用到的进位制:
十进制
Decimal
除了十进制以外,我们还知道哪些进制?
十六进制
二
进
制
八
进
制
通常情况我们用十进制计算,那么计算机用什么进制来计算呢?
二进制
Binary
为什么电脑要用二进制?
电脑是由许多电子元件组成的,电子元件中的电子电路(逻辑电路)有两个状态:开关的接通与断开(电压的高与低)。很显然,这两种状态可以表示数字0和1。
二进制的特点是数码少(只有0和1两个数码),最容易用电子元件实现,所以电脑采用二进制。
将数字、文字、图形、声音、视频等信息转换为二进制数,电脑就可以处理这些形态的信息了。
0
1
0
1
0
1
十进制的结构:
1、有十个基本数字:
0,1,2,3,4,5,6,7,8,9
2、采用逢
的进位规则
十进一
3、采用位权表示法,即一个数码在不同位置上所代表的值不同
什么是二进制呢?我们先来看十进制的结构
例如
:
3578=3000+500+70+8
=3×103+5×102+7×101+8×100
这里个位(100)、十位(101)、百位(102),我们就称为位权
二进制基本结构:
1、有两个基本数字:
2、采用逢
的进位规则
3、采用位权表示法,即一个数码在不同位置上所代表的值不同
例:110101=1×25+1×24+0×23+1×22+0×21+1×20
0和1
二进一
二进制的计算(逢二进一,借一当二)
0
+
0
——
0
0
+
1
——
1
1
+
0
——
1
1
+
1
——
10
运算是计算机最基本的运算功能,包括加、减、乘、除四则运算,其基础是二进制的加法。
1101001+101111=10011000
1101001+101111=?
1101001
+
101111
—————
0
0
0
1
1
0
0
1
二进制的计算(逢二进一)
二进制运算用竖式计算
10110011
101001
+
11011100
10110011
101001
-
10001010
10110011
101
×
10110011
+
10110011
1101111111
试一试
1101+101=
1111+1011=
10010
11010
数的进制的表示
为了区别二进制数和十进制数,通常给数加下标来表示数的进制。
如
(10110)2二进制数,
(16)10十进制数,
(25771)8八进制数,
(2EC9F)16十六进制。
B二进制
D十进制
O八进制
H十六进制
R进制数的表示
除了二进制、十进制以外,计算机中还常常使用八进制和十六进制。
八进制:0、1、2、3、4、5、6、7
十六进制:0、1、2、3、4、5、6、7、8、9、
A(10)、B(11)、C(12)、D(13)、E(14)、F(15)
进制之间的转换
1
R进制转十进制
二进制转换为十进制
1
0
1
1
1
0
1
2
3
4
二
转
十
=
1
24+0
23+1
22+1
21+1
20
=
16
+
0
+
4
+
2
+
1
=
23
即:(10111)2
=(23)10
进制的转换
十六进制转换为十进制
按位权展开
(17)16=1×161+7×160=16+7=(23)10
R进制数转换成十进制数
二进制数要转换成十进制数非常简单,整数部分将每一位数字乘以它的权Rn-1,再以十进制的方法相加即可得到十进制数(注意,小数点右侧相邻位的权为R-1,从左向右,每移一位,幂次减1)。
小试牛刀
(1507.1)8=(?)10
(2AF5)16=(?)10
2
十进制转二进制
整数部分
整数部分:“除基取余倒排序”。
用十进制数除以目标进制基数,直至商等于0为止,逆序排列余数即可得到与该十进制相对应的二进制数各位的数值。
(14)10
=
(
?)2
2|14…………0
7
(14)10
=
(
1110)2
2|
…………1
3
2|
…………1
1
2|
…………1
0
十进制转化为二进制的方法(整数部分):
14D=1110B
将(236)D转换成二进制。
练习
小数部分
小数部分:“乘基取整顺排序”。
小数乘以目标数制的基数,第一次相乘结果的整数部分为目的数的最高位,将其小数部分再乘基数依次记下整数部分,反复进行下去,直到乘积的小数部分为“0”,或满足要求的精度为止。
十进制转化为二进制的方法(小数部分):
0.8125x2
=
1.625...1
(0.8125)10=(0.1101)2
(0.8125)10=(?)2
0.625x2
=
1.25....1
0.25x2
=
0.5.....0
0.5x2
=
1
.....1
十进制转化为R进制的方法:
方法:基数乘除法
整数部分:除基取余倒排序
小数部分:乘基取整顺排序
然后再将转换的两部分合起来
十进制与八、十六进制之间的转换
十进制转八进制或者十六进制有两种方法
法一:间接法—把十进制转成二进制,然后再由二进制转成八进制或者十六进制。
法二:直接法—用短除法把十进制转八进制或者十六进制按照除8或者16取余,直到商为0为止。
二进制转八进制
3
二进制转换为八进制
如:011
010
111
其分成三个组对应如下
三位截取法:二进制中的每三位数对应八进制中的一位数。如此对二进制进行分组,每三位分一组,同时对应着八进制的一位数字。不足三位的,就在最高位前加“0”补足。
结果为:
(11010111)2=(327)8
3
2
7
(11010111.0100111)2
=
练习
八进制转换为二进制
例如
(650)8---(
)2
(7521)8---(
)2
将每一位八进制数用三位相应的二进制数表示,即可
110
101
010
111
101
010
001
二进制转十六进制
4
二进制转换为十六进制
如:1010
1110
0011
四位截取法:二进制中的每四位数对应十六进制中的一位数。如此对二进制进行分组,每四位分一组,同时对应着十六进制的一位数字。
不足四位的,就在最高位前加“0”补足。
(101011100011)2=(AE3)16
A
E
3
十六进制转换为二进制
例如:(A97)16---(
)2
(C757)16---(
)2
将每一位十六进制数用四位相应的二进制数表示,即可完成转换。
1010
1001
111
1100
0111
0101
0111
课堂练习:
1.十进制数78的二进制编码是:___________
2.二进制数100101转换为十进制数是________
1001110
37
3.将二进制代码100101101100101转换为十六进制代码:________
4.将十六进制数7A60FH转换为二进制代码_______________________
4
B
6
5
0111,1010,0110,0000,1111
(1)11010.1B=(
)D
(2)101011B=(
)D
(3)10111B=(
)D
=0
20+1
21+0
22+1
23+1
24
++1
2-1
=1
20+1
21+0
22+1
23+0
24+1
25
=1
20+1
21+1
22+0
23+1
24
26.5
42
22
课后练习:
单位:
计算机存储信息的最小单位是位(bit),简写为b。二进制的一个“0”或一个“1”占一个位。
计算机存储容量的基本单位是字节(Byte),简写为B。一个标准英文字母占一个字节,一个标准汉字占二个字节。
1B=(
)b
1GB=(
)MB=(
)KB
=(
)B
1024b=(
)B
=
(
)KB
8
1024
10242
10243
1024/8
1024/8/1024
数据与计算
信息技术必修1
第一章
数据与信息
数据
什么是数据呢?其实数据就在我们身边。
在日常生活中,人们常用符号来表达客观事物。例如:180cm、70kg、36.5℃可以分别代表人的身高、体重、体温情况;200㎡、600m?、120km/h可以分别表示物体的面积、体积、速度情况,都是数据。
数据可以用来描述不同事物的特征。
数据可用于描述事物。
数据是信息的载体。
1.1数据及其特征
数据
数据是现实世界客观事物的符号记录,是信息的载体,是计算机加工的对象。
在计算机科学中,数据是对所有输入计算机并被计算机识别、存储和处理的符号的总称,是联系现实世界和计算机世界的途径。
生活中的各种符号
现实世界中的各种符号
包括图形、图像、视频、音频、文本(文字、数字、数值、字符)等数值型和非数值型符号。
各种现实世界中的符号都可以被计算机转化为二进制数,进行各种逻辑运算,处理成有意义的数据;然后将计算机运算的二进制数转换成现实世界的视、听、触等各种感觉的信息。
如:
180cm在计算机中转换成二进制:“180”在计算机中表示为10110100;字符“cm”在计算机中表示为0110001101101101;合在一起变为“10110100
0110001101101101”
在大数据时代,数据不仅是信息的载体,也是人们提取信息、做出决策的重要依据,成为人们认识和理解现实世界客观事物的重要资源。
数据的基本特征
二进制。在计算机中,数据以二进制的形式存储、加工。
语义性。语义是将数据符号解释为客观世界的事物。
分散性。数据是分散的记录,分别记录不同客观事物的运动状态。
多样性和感知性。数据记录的形式是多样的、可看的、可听的、可感知的,如图形、图像、视频、音频、文本等。
课堂练习
1.人们用数据记录自然现象与社会发展,数据可以用来描述不同事物的特征。(
)
2.数据是现实世界客观事物的符号记录,是信息的载体,不能用计算机进行加工。(
)
3.以下关于数据的说法正确的是(
)
A.
数据是计算机被发明之后产生的,所以在古代没有数据。
B.
数据的记录过程一定需要人的参与。
C.
数据就是信息,信息就是数据。
D.
数据在人们的生活中正扮演着越来越重要的作用。
对
错
D
我们日常生活中最常用到的进位制:
十进制
Decimal
除了十进制以外,我们还知道哪些进制?
十六进制
二
进
制
八
进
制
通常情况我们用十进制计算,那么计算机用什么进制来计算呢?
二进制
Binary
为什么电脑要用二进制?
电脑是由许多电子元件组成的,电子元件中的电子电路(逻辑电路)有两个状态:开关的接通与断开(电压的高与低)。很显然,这两种状态可以表示数字0和1。
二进制的特点是数码少(只有0和1两个数码),最容易用电子元件实现,所以电脑采用二进制。
将数字、文字、图形、声音、视频等信息转换为二进制数,电脑就可以处理这些形态的信息了。
0
1
0
1
0
1
十进制的结构:
1、有十个基本数字:
0,1,2,3,4,5,6,7,8,9
2、采用逢
的进位规则
十进一
3、采用位权表示法,即一个数码在不同位置上所代表的值不同
什么是二进制呢?我们先来看十进制的结构
例如
:
3578=3000+500+70+8
=3×103+5×102+7×101+8×100
这里个位(100)、十位(101)、百位(102),我们就称为位权
二进制基本结构:
1、有两个基本数字:
2、采用逢
的进位规则
3、采用位权表示法,即一个数码在不同位置上所代表的值不同
例:110101=1×25+1×24+0×23+1×22+0×21+1×20
0和1
二进一
二进制的计算(逢二进一,借一当二)
0
+
0
——
0
0
+
1
——
1
1
+
0
——
1
1
+
1
——
10
运算是计算机最基本的运算功能,包括加、减、乘、除四则运算,其基础是二进制的加法。
1101001+101111=10011000
1101001+101111=?
1101001
+
101111
—————
0
0
0
1
1
0
0
1
二进制的计算(逢二进一)
二进制运算用竖式计算
10110011
101001
+
11011100
10110011
101001
-
10001010
10110011
101
×
10110011
+
10110011
1101111111
试一试
1101+101=
1111+1011=
10010
11010
数的进制的表示
为了区别二进制数和十进制数,通常给数加下标来表示数的进制。
如
(10110)2二进制数,
(16)10十进制数,
(25771)8八进制数,
(2EC9F)16十六进制。
B二进制
D十进制
O八进制
H十六进制
R进制数的表示
除了二进制、十进制以外,计算机中还常常使用八进制和十六进制。
八进制:0、1、2、3、4、5、6、7
十六进制:0、1、2、3、4、5、6、7、8、9、
A(10)、B(11)、C(12)、D(13)、E(14)、F(15)
进制之间的转换
1
R进制转十进制
二进制转换为十进制
1
0
1
1
1
0
1
2
3
4
二
转
十
=
1
24+0
23+1
22+1
21+1
20
=
16
+
0
+
4
+
2
+
1
=
23
即:(10111)2
=(23)10
进制的转换
十六进制转换为十进制
按位权展开
(17)16=1×161+7×160=16+7=(23)10
R进制数转换成十进制数
二进制数要转换成十进制数非常简单,整数部分将每一位数字乘以它的权Rn-1,再以十进制的方法相加即可得到十进制数(注意,小数点右侧相邻位的权为R-1,从左向右,每移一位,幂次减1)。
小试牛刀
(1507.1)8=(?)10
(2AF5)16=(?)10
2
十进制转二进制
整数部分
整数部分:“除基取余倒排序”。
用十进制数除以目标进制基数,直至商等于0为止,逆序排列余数即可得到与该十进制相对应的二进制数各位的数值。
(14)10
=
(
?)2
2|14…………0
7
(14)10
=
(
1110)2
2|
…………1
3
2|
…………1
1
2|
…………1
0
十进制转化为二进制的方法(整数部分):
14D=1110B
将(236)D转换成二进制。
练习
小数部分
小数部分:“乘基取整顺排序”。
小数乘以目标数制的基数,第一次相乘结果的整数部分为目的数的最高位,将其小数部分再乘基数依次记下整数部分,反复进行下去,直到乘积的小数部分为“0”,或满足要求的精度为止。
十进制转化为二进制的方法(小数部分):
0.8125x2
=
1.625...1
(0.8125)10=(0.1101)2
(0.8125)10=(?)2
0.625x2
=
1.25....1
0.25x2
=
0.5.....0
0.5x2
=
1
.....1
十进制转化为R进制的方法:
方法:基数乘除法
整数部分:除基取余倒排序
小数部分:乘基取整顺排序
然后再将转换的两部分合起来
十进制与八、十六进制之间的转换
十进制转八进制或者十六进制有两种方法
法一:间接法—把十进制转成二进制,然后再由二进制转成八进制或者十六进制。
法二:直接法—用短除法把十进制转八进制或者十六进制按照除8或者16取余,直到商为0为止。
二进制转八进制
3
二进制转换为八进制
如:011
010
111
其分成三个组对应如下
三位截取法:二进制中的每三位数对应八进制中的一位数。如此对二进制进行分组,每三位分一组,同时对应着八进制的一位数字。不足三位的,就在最高位前加“0”补足。
结果为:
(11010111)2=(327)8
3
2
7
(11010111.0100111)2
=
练习
八进制转换为二进制
例如
(650)8---(
)2
(7521)8---(
)2
将每一位八进制数用三位相应的二进制数表示,即可
110
101
010
111
101
010
001
二进制转十六进制
4
二进制转换为十六进制
如:1010
1110
0011
四位截取法:二进制中的每四位数对应十六进制中的一位数。如此对二进制进行分组,每四位分一组,同时对应着十六进制的一位数字。
不足四位的,就在最高位前加“0”补足。
(101011100011)2=(AE3)16
A
E
3
十六进制转换为二进制
例如:(A97)16---(
)2
(C757)16---(
)2
将每一位十六进制数用四位相应的二进制数表示,即可完成转换。
1010
1001
111
1100
0111
0101
0111
课堂练习:
1.十进制数78的二进制编码是:___________
2.二进制数100101转换为十进制数是________
1001110
37
3.将二进制代码100101101100101转换为十六进制代码:________
4.将十六进制数7A60FH转换为二进制代码_______________________
4
B
6
5
0111,1010,0110,0000,1111
(1)11010.1B=(
)D
(2)101011B=(
)D
(3)10111B=(
)D
=0
20+1
21+0
22+1
23+1
24
++1
2-1
=1
20+1
21+0
22+1
23+0
24+1
25
=1
20+1
21+1
22+0
23+1
24
26.5
42
22
课后练习:
单位:
计算机存储信息的最小单位是位(bit),简写为b。二进制的一个“0”或一个“1”占一个位。
计算机存储容量的基本单位是字节(Byte),简写为B。一个标准英文字母占一个字节,一个标准汉字占二个字节。
1B=(
)b
1GB=(
)MB=(
)KB
=(
)B
1024b=(
)B
=
(
)KB
8
1024
10242
10243
1024/8
1024/8/1024
同课章节目录
- 第一章 数据与信息
- 项目范例 体验庆祝国庆多媒体作品的数据与信息处理
- 1.1 数据及其特征
- 1.2 数据编码
- 1.3 信息及其特征
- 第二章 知识与数字化学习
- 项目范例 运用数字化工具探究数理知识
- 2.1 知识与智慧
- 2.2 数字化学习与创新
- 第三章 算法基础
- 项目范例 设计从A市到B市耗时最少的旅行路线方案
- 3.1 体验计算机解决问题的过程
- 3.2 算法及其描述
- 3.3 计算机程序与程序设计语言
- 第四章 程序设计基础
- 项目范例 设计购买纪念品的最佳方案
- 4.1 程序设计语言的基础知识
- 4.2 运用顺序结构描述问题求解过程
- 4.3 运用选择结构描述问题求解过程
- 4.4 运用循环结构描述问题求解过程
- 第五章 数据处理和可视化表达
- 项目范例 网络购物平台客户行为数据分析和可视化表达
- 5.1 认识大数据
- 5.2 数据的采集
- 5.3 数据的分析
- 5.4 数据的可视化表达
- 第六章 人工智能及其应用
- 项目范例 剖析空调企业智能客服机器人
- 6.1 认识人工智能
- 6.2 人工智能的应用
