人教版数学九年级下册26.2实际问题与反比例函数课件(第一课时 33张)
文档属性
| 名称 | 人教版数学九年级下册26.2实际问题与反比例函数课件(第一课时 33张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览










文档简介
26.2 实际问题与反比例函数
反比例函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
反比例函数
图象
性质
k 的几何意义
画法
形状
图象位置
增减性
列表、描点、连线
双曲线
学习目标
1.体会数学与现实生活的紧密联系,增强应用意识,提高运用代数方法解决问题的能力.
2.能够通过分析实际问题中变量之间的关系,建立反比例函数模型解决问题,进一步提高运用函数图象、性质的综合能力.
3.能够根据实际问题确定自变量的取值范围.
课堂导入
拉面又叫甩面、扯面、抻面,是中国城乡独具地方风味的一种传统面食.
课堂导入
你还能举出我们在日常生活、生产或学习中具有反比例函数关系的实例吗?
如果要把体积为 15 cm3 的面团做成拉面,你能写出面条的总长度 y (单位:cm) 与面条粗细(横截面积) S (单位:cm2)的函数关系式吗?
新知探究
知识点:反比例函数在实际问题中的应用
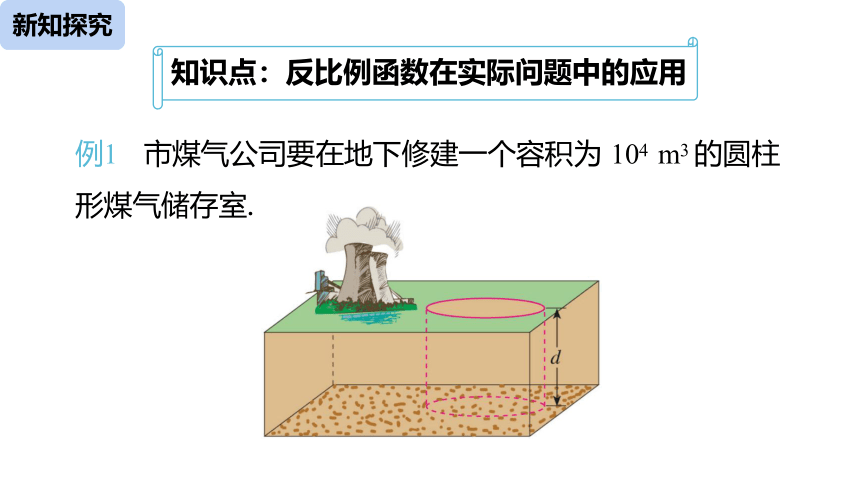
例1 市煤气公司要在地下修建一个容积为 104 m3 的圆柱形煤气储存室.
新知探究
解:根据圆柱的体积公式,得 Sd =104,
∴ S 关于d 的函数解析式为
(1) 储存室的底面积 S (单位:m2) 与其深度 d (单位:m)有怎样的函数关系?
新知探究
(2) 公司决定把储存室的底面积 S 定为 500 m2,施工队施工时应该向地下掘进多深?
解得 d = 20 (m).
如果把储存室的底面积定为 500 m?,施工时应向地下掘进 20 m 深.
解:把 S = 500 代入 ,得
新知探究
(3) 当施工队按 (2) 中的计划掘进到地下 15 m 时,公司临时改变计划,把储存室的深度改为 15 m. 相应地,储存室的底面积应改为多少 (结果保留小数点后两位)?
解得 S≈666.67 (m?).
当储存室的深度为15 m 时,底面积应改为 666.67 m?.
解:根据题意,把 d =15 代入 ,得
新知探究
第(2)问和第(3)问与过去所学的解分式方程和求代数式的值的问题有何联系?
第(2)问实际上是已知函数 S 的值,求自变量 d 的取值,第(3)问则是与第(2)问相反.
新知探究
分析:根据“平均装货速度×装货天数=货物的总量”,可以求出轮船装载货物的总量;再根据“平均卸货速度=货物的总量÷卸货天数”,得到 v 关于 t 的函数解析式.
例2 码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1) 轮船到达目的地后开始卸货,平均卸货速度v (单位:吨/天)与卸货天数 t 之间有怎样的函数关系?
新知探究
例2 码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1) 轮船到达目的地后开始卸货,平均卸货速度v (单位:吨/天)与卸货天数 t 之间有怎样的函数关系?
解:设轮船上的货物总量为 k 吨,根据题意得
k =30×8=240,
所以 v 关于 t 的函数解析式为
新知探究
(2) 由于遇到紧急情况,要求船上的货物不超过 5天卸载完毕,那么平均每天至少要卸载多少吨?
解:把 t =5 代入 ,得
新知探究
方法总结:在解决与反比例函数相关的实际问题中,若题目要求“至多”“至少”,可以利用反比例函数的增减性来解答 .
从结果可以看出,如果全部货物恰好用 5 天卸载完,那么平均每天卸载 48 吨.观察求得的反比例函数解析式可知,当t >0时, t 越小,v 越大.这样若货物不超过 5 天卸载完,则平均每天至少要卸载 48 吨.
新知探究
建立反比例函数解析式的常用方法:
(1)待定系数法:若题目提供的信息中明确此函数是反比例函数,则设函数解析式为 ????=???????? (k为常数,k≠0),然后求出 k 的值;
(2)列方程法:若题目所给的信息中两个变量之间的函数关系不明确,通常列出关于两个变量的方程,通过变形得到反比例函数解析式.
?
新知探究
常见的反比例函数在实际生活中应用的实例:
(1)当路程 s 一定时,时间 t 与平均速度 v 成反比例,即 ????=???????? (s 是常数).
(2)当三角形的面积 S 一定时,三角形的一边 a 与该边上的高 h 成反比例,即 ????=2????h (S 是常数).
?
跟踪训练
1.如图,某玻璃器皿制造公司要制造一种容积为1 L (1 L=1 dm3)的圆锥形漏斗.
(1) 漏斗口的面积 S (单位:dm2)与漏斗的深 d (单位:dm) 有怎样的函数关系?
解:
圆锥体容积公式 ????=????????????????.
?
(2) 如果漏斗口的面积为100 cm2,那么漏斗的深为多少?
解:100 cm2=1 dm2,把 S =1 代入解析式,得 d =3,所以漏斗的深为 3 dm.
100 cm2=1 dm2
跟踪训练
2.如图是某一蓄水池的排水速度 v ( m3/h)与排完水池中的水所用的时间 t (h)之间的函数图象.
(1)请你根据图象提供的信息求出此蓄水池的总蓄水量;
解:(1)此蓄水池的总蓄水量为 4000×12=48000(m3 ).
总蓄水量=排水速度×时间
跟踪训练
(2)写出此函数的解析式;
解:(2)此函数的解析式为 ????=48000????.
?
(3)若要 8 h 排完水池中的水,那么该蓄水池的排水速度应该是多少?
解:(3)当 t=8 h 时, ????=480008=6000(m3/h).
答:若要8 h排完水池中的水,那么该蓄水池的排水速度应该是6000 m3/h.
?
跟踪训练
随堂练习
1.某村耕地总面积为 50 公顷,且该村人均耕地面
积 y (单位:公顷)与总人口 x (单位:人)的函数
关系图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积 y 与总人口 x 成正比例
C.若该村人均耕地面积为 2 公顷,则总人口有 100 人
D.当该村总人口为 50人时,人均耕地面积为1 公顷
D
减少
反比例
50÷2=25
随堂练习
2.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的两边长分别为 x,y,剪去部分的面积为20,若 2≤ x ≤10,则 y 关于 x 的函数图象是( )
xy =10
A
随堂练习
实际问题中反比例函数的图象往往只是双曲线的一支或一支的一部分,注意实际问题中自变量的取值范围.
随堂练习
3.一辆汽车匀速通过某段公路,所需时间 t (h)与行驶速度 v (km/h)满足函数关系:????=???????? ,其图象为如图所示的一段曲线,且端点为 A(40,1)和 B(m,0.5).
(1)求 k 和 m 的值;
?
解:(1)将 A(40,1)代入 ????=???????? ,
得 1=????40 ,解得 k=40. 所以 ????=40????.
将B(m,0.5)代入 ????=40???? ,得 0.5=40???? ,所以 m=80.
?
随堂练习
(2)若行驶速度不得超过 60 km/h,则汽车通过该路段最少需要多长时间?
解:(2)当 v=60 km/h时, ????=4060=23 (h).
结合函数图象可知,汽车通过该路段最
少需要 23 h.
?
课堂小结
反比例函数在实际问题中的应用
建立函数解析式
自变量取值范围
待定系数法
列方程法
解析式本身的限制
实际问题的具体要求
对接中考
1.(2019·淮安中考)当矩形面积一定时,下列图象中能表示它的长 y 和宽 x 之间函数关系的是( )
B
面积=长×宽
A B C D
对接中考
2.(2017·雅安中考)校园超市以 4 元/件购进某物品,为制定该物品合理的销售价格,对该物品进行试销调查.发现每天调整不同的销售价,其销售总金额为定值,其中某天该物品的售价为 6 元/件时,销售量为 50 件.
(1) 设售价为 x 元/件时,销售量为 y 件.请写出 y 与 x 的函数关系式;
解:(1)依题意得xy=50×6=300,则????=300???? .
?
xy =50×6=300
对接中考
(2)若超市考虑学生的消费实际,计划将该物品每天的销售利润定为 60 元,则该物品的售价应定为多少元/件?
解:(2)设该物品的售价应定为x元/件,
依题意得60=300?????????4,
解得x=5,
经检验,x=5是方程的根且符合题意.
答:该物品的售价应定为5元/件.
?
对接中考
3.(2019·杭州中考)方方驾驶小汽车匀速地从 A 地行驶到 B 地,行驶路程为480千米,设小汽车的行驶时间为 t (单位:时),行驶速度为 v (单位:千米/小时),且全程速度限定为不超过120千米/小时.
(1)求 v 关于 t 的函数解析式;
里程=速度×时间
v ≤ 120→t ≥ 4
解:(1)由题意得 vt =480,∴ ????=480???? .
∵ v ≤120,∴ t ≥4.
∴ v关于 t 的函数解析式为 ????=480????(t ≥4).
?
对接中考
(2)方方上午8点驾驶小汽车从 A 地出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达 B 地,求小汽车行驶速度 v 的范围.
解:(2)①8点至12点48分时间长为 245 小时,8点至14点时间长为 6 小时.
将 t =6 代入????=480???? ,得 v =80;将 ????=245 代入 ????=480???? ,得 v =100.
故小汽车行驶速度 v 的范围为:80 千米/时≤ v ≤100 千米/时.
?
对接中考
②方方能否在当天11点30分前到达 B 地?说明理由.
解:(2) ②方方不能在当天11点30分前到达 B 地.理由如下:
8点至11点30分时间长为 72 小时.
将 ????=72 代入 ????=480???? ,得 ????=9607>120 .
故方方不能在当天11点30分前到达 B 地.
?
课后作业
请完成课本后习题第7题.
反比例函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
反比例函数
图象
性质
k 的几何意义
画法
形状
图象位置
增减性
列表、描点、连线
双曲线
学习目标
1.体会数学与现实生活的紧密联系,增强应用意识,提高运用代数方法解决问题的能力.
2.能够通过分析实际问题中变量之间的关系,建立反比例函数模型解决问题,进一步提高运用函数图象、性质的综合能力.
3.能够根据实际问题确定自变量的取值范围.
课堂导入
拉面又叫甩面、扯面、抻面,是中国城乡独具地方风味的一种传统面食.
课堂导入
你还能举出我们在日常生活、生产或学习中具有反比例函数关系的实例吗?
如果要把体积为 15 cm3 的面团做成拉面,你能写出面条的总长度 y (单位:cm) 与面条粗细(横截面积) S (单位:cm2)的函数关系式吗?
新知探究
知识点:反比例函数在实际问题中的应用
例1 市煤气公司要在地下修建一个容积为 104 m3 的圆柱形煤气储存室.
新知探究
解:根据圆柱的体积公式,得 Sd =104,
∴ S 关于d 的函数解析式为
(1) 储存室的底面积 S (单位:m2) 与其深度 d (单位:m)有怎样的函数关系?
新知探究
(2) 公司决定把储存室的底面积 S 定为 500 m2,施工队施工时应该向地下掘进多深?
解得 d = 20 (m).
如果把储存室的底面积定为 500 m?,施工时应向地下掘进 20 m 深.
解:把 S = 500 代入 ,得
新知探究
(3) 当施工队按 (2) 中的计划掘进到地下 15 m 时,公司临时改变计划,把储存室的深度改为 15 m. 相应地,储存室的底面积应改为多少 (结果保留小数点后两位)?
解得 S≈666.67 (m?).
当储存室的深度为15 m 时,底面积应改为 666.67 m?.
解:根据题意,把 d =15 代入 ,得
新知探究
第(2)问和第(3)问与过去所学的解分式方程和求代数式的值的问题有何联系?
第(2)问实际上是已知函数 S 的值,求自变量 d 的取值,第(3)问则是与第(2)问相反.
新知探究
分析:根据“平均装货速度×装货天数=货物的总量”,可以求出轮船装载货物的总量;再根据“平均卸货速度=货物的总量÷卸货天数”,得到 v 关于 t 的函数解析式.
例2 码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1) 轮船到达目的地后开始卸货,平均卸货速度v (单位:吨/天)与卸货天数 t 之间有怎样的函数关系?
新知探究
例2 码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1) 轮船到达目的地后开始卸货,平均卸货速度v (单位:吨/天)与卸货天数 t 之间有怎样的函数关系?
解:设轮船上的货物总量为 k 吨,根据题意得
k =30×8=240,
所以 v 关于 t 的函数解析式为
新知探究
(2) 由于遇到紧急情况,要求船上的货物不超过 5天卸载完毕,那么平均每天至少要卸载多少吨?
解:把 t =5 代入 ,得
新知探究
方法总结:在解决与反比例函数相关的实际问题中,若题目要求“至多”“至少”,可以利用反比例函数的增减性来解答 .
从结果可以看出,如果全部货物恰好用 5 天卸载完,那么平均每天卸载 48 吨.观察求得的反比例函数解析式可知,当t >0时, t 越小,v 越大.这样若货物不超过 5 天卸载完,则平均每天至少要卸载 48 吨.
新知探究
建立反比例函数解析式的常用方法:
(1)待定系数法:若题目提供的信息中明确此函数是反比例函数,则设函数解析式为 ????=???????? (k为常数,k≠0),然后求出 k 的值;
(2)列方程法:若题目所给的信息中两个变量之间的函数关系不明确,通常列出关于两个变量的方程,通过变形得到反比例函数解析式.
?
新知探究
常见的反比例函数在实际生活中应用的实例:
(1)当路程 s 一定时,时间 t 与平均速度 v 成反比例,即 ????=???????? (s 是常数).
(2)当三角形的面积 S 一定时,三角形的一边 a 与该边上的高 h 成反比例,即 ????=2????h (S 是常数).
?
跟踪训练
1.如图,某玻璃器皿制造公司要制造一种容积为1 L (1 L=1 dm3)的圆锥形漏斗.
(1) 漏斗口的面积 S (单位:dm2)与漏斗的深 d (单位:dm) 有怎样的函数关系?
解:
圆锥体容积公式 ????=????????????????.
?
(2) 如果漏斗口的面积为100 cm2,那么漏斗的深为多少?
解:100 cm2=1 dm2,把 S =1 代入解析式,得 d =3,所以漏斗的深为 3 dm.
100 cm2=1 dm2
跟踪训练
2.如图是某一蓄水池的排水速度 v ( m3/h)与排完水池中的水所用的时间 t (h)之间的函数图象.
(1)请你根据图象提供的信息求出此蓄水池的总蓄水量;
解:(1)此蓄水池的总蓄水量为 4000×12=48000(m3 ).
总蓄水量=排水速度×时间
跟踪训练
(2)写出此函数的解析式;
解:(2)此函数的解析式为 ????=48000????.
?
(3)若要 8 h 排完水池中的水,那么该蓄水池的排水速度应该是多少?
解:(3)当 t=8 h 时, ????=480008=6000(m3/h).
答:若要8 h排完水池中的水,那么该蓄水池的排水速度应该是6000 m3/h.
?
跟踪训练
随堂练习
1.某村耕地总面积为 50 公顷,且该村人均耕地面
积 y (单位:公顷)与总人口 x (单位:人)的函数
关系图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积 y 与总人口 x 成正比例
C.若该村人均耕地面积为 2 公顷,则总人口有 100 人
D.当该村总人口为 50人时,人均耕地面积为1 公顷
D
减少
反比例
50÷2=25
随堂练习
2.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的两边长分别为 x,y,剪去部分的面积为20,若 2≤ x ≤10,则 y 关于 x 的函数图象是( )
xy =10
A
随堂练习
实际问题中反比例函数的图象往往只是双曲线的一支或一支的一部分,注意实际问题中自变量的取值范围.
随堂练习
3.一辆汽车匀速通过某段公路,所需时间 t (h)与行驶速度 v (km/h)满足函数关系:????=???????? ,其图象为如图所示的一段曲线,且端点为 A(40,1)和 B(m,0.5).
(1)求 k 和 m 的值;
?
解:(1)将 A(40,1)代入 ????=???????? ,
得 1=????40 ,解得 k=40. 所以 ????=40????.
将B(m,0.5)代入 ????=40???? ,得 0.5=40???? ,所以 m=80.
?
随堂练习
(2)若行驶速度不得超过 60 km/h,则汽车通过该路段最少需要多长时间?
解:(2)当 v=60 km/h时, ????=4060=23 (h).
结合函数图象可知,汽车通过该路段最
少需要 23 h.
?
课堂小结
反比例函数在实际问题中的应用
建立函数解析式
自变量取值范围
待定系数法
列方程法
解析式本身的限制
实际问题的具体要求
对接中考
1.(2019·淮安中考)当矩形面积一定时,下列图象中能表示它的长 y 和宽 x 之间函数关系的是( )
B
面积=长×宽
A B C D
对接中考
2.(2017·雅安中考)校园超市以 4 元/件购进某物品,为制定该物品合理的销售价格,对该物品进行试销调查.发现每天调整不同的销售价,其销售总金额为定值,其中某天该物品的售价为 6 元/件时,销售量为 50 件.
(1) 设售价为 x 元/件时,销售量为 y 件.请写出 y 与 x 的函数关系式;
解:(1)依题意得xy=50×6=300,则????=300???? .
?
xy =50×6=300
对接中考
(2)若超市考虑学生的消费实际,计划将该物品每天的销售利润定为 60 元,则该物品的售价应定为多少元/件?
解:(2)设该物品的售价应定为x元/件,
依题意得60=300?????????4,
解得x=5,
经检验,x=5是方程的根且符合题意.
答:该物品的售价应定为5元/件.
?
对接中考
3.(2019·杭州中考)方方驾驶小汽车匀速地从 A 地行驶到 B 地,行驶路程为480千米,设小汽车的行驶时间为 t (单位:时),行驶速度为 v (单位:千米/小时),且全程速度限定为不超过120千米/小时.
(1)求 v 关于 t 的函数解析式;
里程=速度×时间
v ≤ 120→t ≥ 4
解:(1)由题意得 vt =480,∴ ????=480???? .
∵ v ≤120,∴ t ≥4.
∴ v关于 t 的函数解析式为 ????=480????(t ≥4).
?
对接中考
(2)方方上午8点驾驶小汽车从 A 地出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达 B 地,求小汽车行驶速度 v 的范围.
解:(2)①8点至12点48分时间长为 245 小时,8点至14点时间长为 6 小时.
将 t =6 代入????=480???? ,得 v =80;将 ????=245 代入 ????=480???? ,得 v =100.
故小汽车行驶速度 v 的范围为:80 千米/时≤ v ≤100 千米/时.
?
对接中考
②方方能否在当天11点30分前到达 B 地?说明理由.
解:(2) ②方方不能在当天11点30分前到达 B 地.理由如下:
8点至11点30分时间长为 72 小时.
将 ????=72 代入 ????=480???? ,得 ????=9607>120 .
故方方不能在当天11点30分前到达 B 地.
?
课后作业
请完成课本后习题第7题.
