人教版数学九年级下册27.1图形的相似 课时2课件(33张)
文档属性
| 名称 | 人教版数学九年级下册27.1图形的相似 课时2课件(33张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览







文档简介
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
27.1 图形的相似
相 似
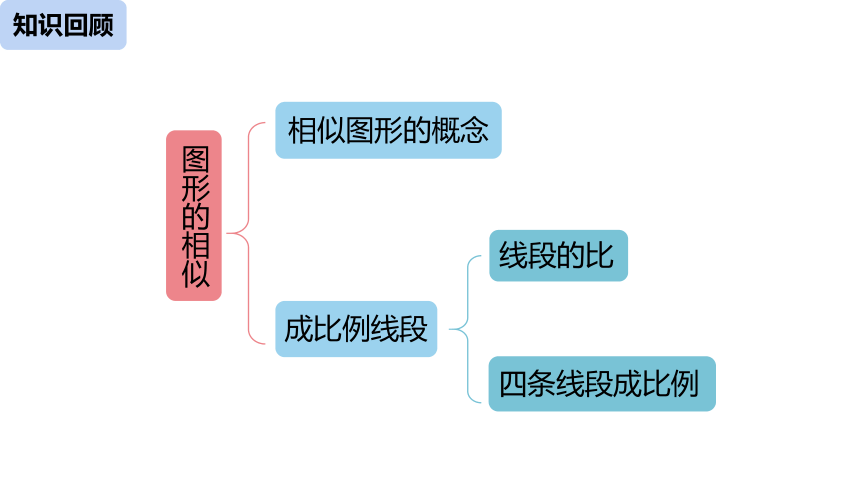
知识回顾
图形的相似
相似图形的概念
成比例线段
线段的比
四条线段成比例
学习目标
1.理解相似多边形的定义.
2.能根据多边形相似进行相关的计算,会根据条件判断两个多边形是否相似.
3.在学习相似图形的过程中,提高对相似图形中的对应关系的认识,增强数学推理能力.
课堂导入
怎样从数学的角度刻画“形状相同”呢?这节课就让我们一起来探究相似多边形吧!
相似!
形状相同的两个多边形相似吗?
新知探究
知识点:相似多边形与相似比
观察图中的两个多边形 ABCDEF 和多边形 A1B1C1D1E1F1,它们的形状相同吗?
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
新知探究
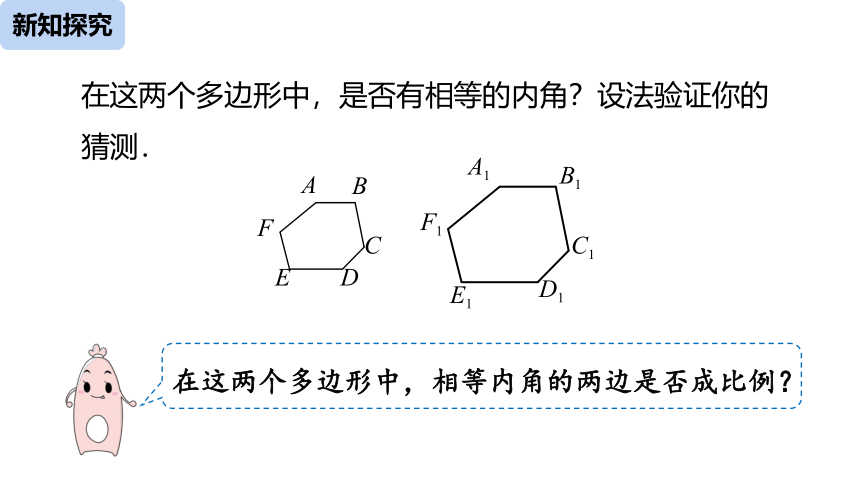
在这两个多边形中,是否有相等的内角?设法验证你的猜测.
在这两个多边形中,相等内角的两边是否成比例?
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
新知探究
请同学们自己动手画一组相似多边形,测量它们的角有怎样的关系?边呢?
是形状相同的多边形都有这种关系呢,还是只有六边形才有呢?
新知探究
定义:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
两个多边形相似,必须同时具备三个条件:
(1)边数相同;
(2)角分别相等;
(3)边成比例.
新知探究
定义:相似多边形对应边的比叫做相似比.
1.相似比的值与两个多边形的顺序有关.例如:若四边形 ABCD 与四边形 A?B?C?D?的相似比为3,则四边形 A?B?C?D?与四边形 ABCD的相似比为 ????????.
2.全等的两个图形的相似比为1.
?
新知探究
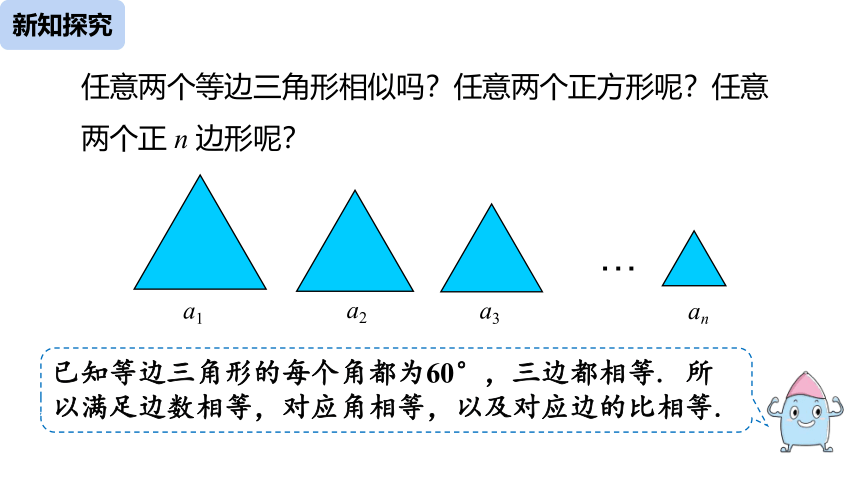
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
a1
a2
a3
an
…
已知等边三角形的每个角都为60°,三边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
新知探究
a1
a2
a3
an
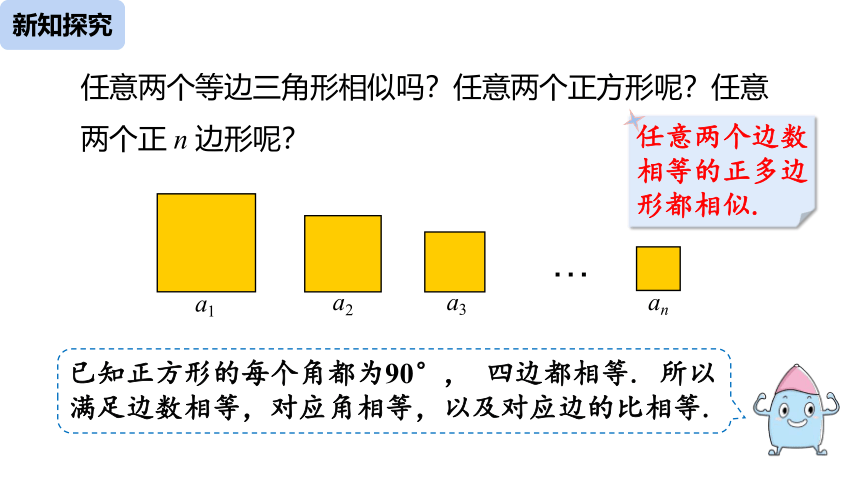
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
已知正方形的每个角都为90°, 四边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
任意两个边数相等的正多边形都相似.
…
新知探究
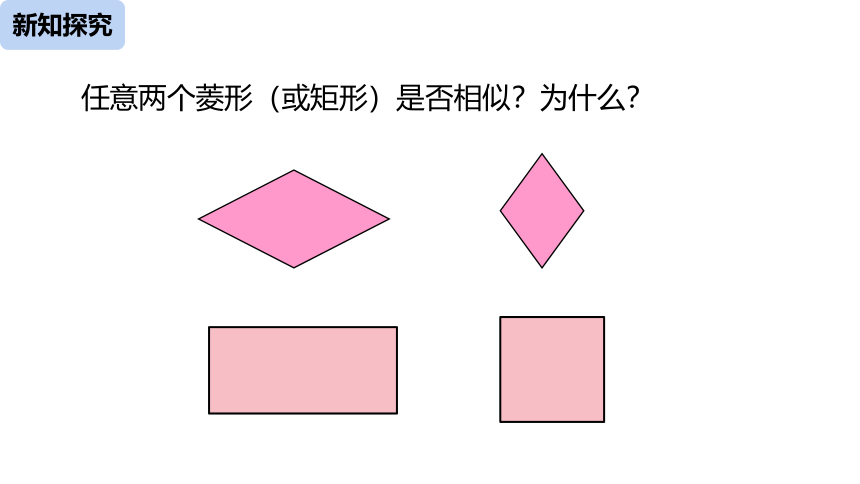
任意两个菱形(或矩形)是否相似?为什么?
新知探究
相似多边形的性质:相似多边形的对应角相等,对应边成比例.
如果两个多边形相似,那么它们的角有什么关系?它们的边呢??
相似多边形的对应角相等,但相等的两个角未必是对应角,要结合图形去观察它们之间的对应关系.
新知探究
活学巧记
两个相似多边形,边数相同形状同;
各角对应都相等,各边对应成比例.
(1)相似多边形的定义可用来判定两个多边形是否相似.
(2)相似多边形的性质常用来求相似多边形未知边的长度或未知角的度数.
新知探究
例 如图,四边形 ABCD 和 EFGH 相似,求角 α,β 的大小和 EH 的长度 x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
新知探究
在四边形 ABCD 中,β=360°-(78°+83°+118°)=81°.
α=∠C=83°,∠A=∠E=118°.
解:∵ 四边形 ABCD 和 EFGH 相似,
∴ 它们的对应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
新知探究
解:∵ 四边形 ABCD 和 EFGH 相似,
∴它们的对应边成比例,由此可得
解得 x = 28 .
,即 .
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
跟踪训练
1.下列说法正确的是( )
A.两个等腰三角形相似
B.两个等腰直角三角形相似
C.两个矩形相似
D.两个平行四边形相似
B
相似多边形对应角相等,对应边成比例.
2.如图是两个相似的四边形,根据已知数据,求 x,y,α 的值.
跟踪训练
解:因为四边形 ABCD 与四边形 ????′????′????′????′相似,
所以∠C′=∠C=83°,且 ????????????′????′=????????????′????′=????????????′????′,即 64=????6=????5,
解得 x=7.5,y=9.
在四边形A'B'C'D' 中,α=360°-∠A'-∠B'-∠C' = 360° -
134° -60° -83°=83°.
?
跟踪训练
随堂练习
1.如图所示,已知四边形 ABCD 中,PQ//AD//BC,AD = 2,BC = 8,若 PQ 把四边形 ABCD 分成两个小四边形,且这两个小四边形相似,求 PQ 的长.
确定两个相似多边形的对应边时,如果边的大小明显,则“长边对长边,短边对短边”.
随堂练习
解:由题意可得,四边形 APQD 与四边形 PBCQ 相似,
所以 ????????????????=???????????????? ,所以 PQ2=AD·BC,
因为 AD = 2,BC = 8,所以 PQ2=2×8=16,所以 PQ = 4.
?
随堂练习
2.小明家有一个矩形相框,其宽为 10 cm,长为 20 cm.小明想做一个与该相框形状完全相同的相框,但手中只有一根作为一边的 30 cm 长的框料,那么小明还要准备的框料的长度为_______cm.
相似
本题中30cm的一边既可以对应原相框的长,又可以对应原相框的宽,所以需分两种情况讨论.
随堂练习
解析:因为两个矩形的形状完全相同,所以它们相似,对应边成比例.设所做相框的另一边长为 x cm,分两种情况讨论:
①当 10????=2030 时,解得 x=15,所以还要准备的框料的长度为 30+15×2 = 60 (cm) ;
②当 1030=20???? 时,解得 x = 60,所以还要准备的框料的长度为 30+60×2 = 150 (cm).
综上所述,小明还要准备 60 cm 或 150 cm 长的框料.
?
随堂练习
3.在 AB =30 m,AD =20 m 的矩形花坛 ABCD 的四周修筑小路.
(1)如果小路的宽均相等,如图所示,那么小路四周所围成的矩形 ????′????′????′????′ 和矩形 ABCD 相似吗?请说明理由.
?
解:(1)矩形 ????′????′????′????′ 和矩形 ABCD 不相似.理由如下:
设小路的宽为 a m,若两个矩形相似,
则 30+2????30=20+2????20 ,
解得 a=0.
∵小路的宽不为0,
∴小路四周所围成的矩形 ????′????′????′????′ 和
矩形 ABCD 不相似.
?
随堂练习
随堂练习
(2)如果相对的两条小路的宽均相等,如图所示,当小路的宽 x 与 y (x?
随堂练习
解:(2)当矩形 ????′????′????′????′ 和矩形 ABCD 相似时,
20+2????20=30+2????30 ,
整理得 3x=2y,
∴ ????????=23 ,
∴ 当小路的宽 x 与 y 的比值为 23 时,小路四周所围成的矩形 ????′????′????′????′ 和矩形 ABCD 相似.
?
课堂小结
相似多边形
概念
相似比
性质
对应角相等
对应边成比例
对接中考
1.(2013·莆田中考)下列四组图形中,一定相似的是( )
A.正方形与矩形
B.正方形与菱形
C.菱形与菱形
D.正五边形与正五边形
D
任意两个边数相等的正多边形相似.
对接中考
2.(2018·重庆中考)制作一块3 m×2 m长方形广告牌的成本是120 元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的 3 倍,那么扩大后长方形广告牌的成本是( )
A.360 元 B.720 元
C.1080 元 D.2160 元
C
面积扩大为原来的 9 倍
对接中考
3.(2017·河北中考)若△ABC 的每条边长增加各自的 10% 得△A′B′C′,则∠B′ 的度数与其对应角∠B 的度数相比( )
A.增加了10% B.减少了10%
C.增加了(1+10%) D.没有改变
D
对应边成比例
对应角相等
课后作业
请完成课本后习题第3、4、 5、6题.
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
27.1 图形的相似
相 似
知识回顾
图形的相似
相似图形的概念
成比例线段
线段的比
四条线段成比例
学习目标
1.理解相似多边形的定义.
2.能根据多边形相似进行相关的计算,会根据条件判断两个多边形是否相似.
3.在学习相似图形的过程中,提高对相似图形中的对应关系的认识,增强数学推理能力.
课堂导入
怎样从数学的角度刻画“形状相同”呢?这节课就让我们一起来探究相似多边形吧!
相似!
形状相同的两个多边形相似吗?
新知探究
知识点:相似多边形与相似比
观察图中的两个多边形 ABCDEF 和多边形 A1B1C1D1E1F1,它们的形状相同吗?
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
新知探究
在这两个多边形中,是否有相等的内角?设法验证你的猜测.
在这两个多边形中,相等内角的两边是否成比例?
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
新知探究
请同学们自己动手画一组相似多边形,测量它们的角有怎样的关系?边呢?
是形状相同的多边形都有这种关系呢,还是只有六边形才有呢?
新知探究
定义:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
两个多边形相似,必须同时具备三个条件:
(1)边数相同;
(2)角分别相等;
(3)边成比例.
新知探究
定义:相似多边形对应边的比叫做相似比.
1.相似比的值与两个多边形的顺序有关.例如:若四边形 ABCD 与四边形 A?B?C?D?的相似比为3,则四边形 A?B?C?D?与四边形 ABCD的相似比为 ????????.
2.全等的两个图形的相似比为1.
?
新知探究
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
a1
a2
a3
an
…
已知等边三角形的每个角都为60°,三边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
新知探究
a1
a2
a3
an
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
已知正方形的每个角都为90°, 四边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
任意两个边数相等的正多边形都相似.
…
新知探究
任意两个菱形(或矩形)是否相似?为什么?
新知探究
相似多边形的性质:相似多边形的对应角相等,对应边成比例.
如果两个多边形相似,那么它们的角有什么关系?它们的边呢??
相似多边形的对应角相等,但相等的两个角未必是对应角,要结合图形去观察它们之间的对应关系.
新知探究
活学巧记
两个相似多边形,边数相同形状同;
各角对应都相等,各边对应成比例.
(1)相似多边形的定义可用来判定两个多边形是否相似.
(2)相似多边形的性质常用来求相似多边形未知边的长度或未知角的度数.
新知探究
例 如图,四边形 ABCD 和 EFGH 相似,求角 α,β 的大小和 EH 的长度 x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
新知探究
在四边形 ABCD 中,β=360°-(78°+83°+118°)=81°.
α=∠C=83°,∠A=∠E=118°.
解:∵ 四边形 ABCD 和 EFGH 相似,
∴ 它们的对应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
新知探究
解:∵ 四边形 ABCD 和 EFGH 相似,
∴它们的对应边成比例,由此可得
解得 x = 28 .
,即 .
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
跟踪训练
1.下列说法正确的是( )
A.两个等腰三角形相似
B.两个等腰直角三角形相似
C.两个矩形相似
D.两个平行四边形相似
B
相似多边形对应角相等,对应边成比例.
2.如图是两个相似的四边形,根据已知数据,求 x,y,α 的值.
跟踪训练
解:因为四边形 ABCD 与四边形 ????′????′????′????′相似,
所以∠C′=∠C=83°,且 ????????????′????′=????????????′????′=????????????′????′,即 64=????6=????5,
解得 x=7.5,y=9.
在四边形A'B'C'D' 中,α=360°-∠A'-∠B'-∠C' = 360° -
134° -60° -83°=83°.
?
跟踪训练
随堂练习
1.如图所示,已知四边形 ABCD 中,PQ//AD//BC,AD = 2,BC = 8,若 PQ 把四边形 ABCD 分成两个小四边形,且这两个小四边形相似,求 PQ 的长.
确定两个相似多边形的对应边时,如果边的大小明显,则“长边对长边,短边对短边”.
随堂练习
解:由题意可得,四边形 APQD 与四边形 PBCQ 相似,
所以 ????????????????=???????????????? ,所以 PQ2=AD·BC,
因为 AD = 2,BC = 8,所以 PQ2=2×8=16,所以 PQ = 4.
?
随堂练习
2.小明家有一个矩形相框,其宽为 10 cm,长为 20 cm.小明想做一个与该相框形状完全相同的相框,但手中只有一根作为一边的 30 cm 长的框料,那么小明还要准备的框料的长度为_______cm.
相似
本题中30cm的一边既可以对应原相框的长,又可以对应原相框的宽,所以需分两种情况讨论.
随堂练习
解析:因为两个矩形的形状完全相同,所以它们相似,对应边成比例.设所做相框的另一边长为 x cm,分两种情况讨论:
①当 10????=2030 时,解得 x=15,所以还要准备的框料的长度为 30+15×2 = 60 (cm) ;
②当 1030=20???? 时,解得 x = 60,所以还要准备的框料的长度为 30+60×2 = 150 (cm).
综上所述,小明还要准备 60 cm 或 150 cm 长的框料.
?
随堂练习
3.在 AB =30 m,AD =20 m 的矩形花坛 ABCD 的四周修筑小路.
(1)如果小路的宽均相等,如图所示,那么小路四周所围成的矩形 ????′????′????′????′ 和矩形 ABCD 相似吗?请说明理由.
?
解:(1)矩形 ????′????′????′????′ 和矩形 ABCD 不相似.理由如下:
设小路的宽为 a m,若两个矩形相似,
则 30+2????30=20+2????20 ,
解得 a=0.
∵小路的宽不为0,
∴小路四周所围成的矩形 ????′????′????′????′ 和
矩形 ABCD 不相似.
?
随堂练习
随堂练习
(2)如果相对的两条小路的宽均相等,如图所示,当小路的宽 x 与 y (x
随堂练习
解:(2)当矩形 ????′????′????′????′ 和矩形 ABCD 相似时,
20+2????20=30+2????30 ,
整理得 3x=2y,
∴ ????????=23 ,
∴ 当小路的宽 x 与 y 的比值为 23 时,小路四周所围成的矩形 ????′????′????′????′ 和矩形 ABCD 相似.
?
课堂小结
相似多边形
概念
相似比
性质
对应角相等
对应边成比例
对接中考
1.(2013·莆田中考)下列四组图形中,一定相似的是( )
A.正方形与矩形
B.正方形与菱形
C.菱形与菱形
D.正五边形与正五边形
D
任意两个边数相等的正多边形相似.
对接中考
2.(2018·重庆中考)制作一块3 m×2 m长方形广告牌的成本是120 元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的 3 倍,那么扩大后长方形广告牌的成本是( )
A.360 元 B.720 元
C.1080 元 D.2160 元
C
面积扩大为原来的 9 倍
对接中考
3.(2017·河北中考)若△ABC 的每条边长增加各自的 10% 得△A′B′C′,则∠B′ 的度数与其对应角∠B 的度数相比( )
A.增加了10% B.减少了10%
C.增加了(1+10%) D.没有改变
D
对应边成比例
对应角相等
课后作业
请完成课本后习题第3、4、 5、6题.
