人教版数学九年级下册27.2.2 相似三角形的性质课件(32张)
文档属性
| 名称 | 人教版数学九年级下册27.2.2 相似三角形的性质课件(32张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1017.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 21:59:56 | ||
图片预览










文档简介
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
27.2.2 相似三角形的性质
相 似
知识回顾
相似三角形的判定方法有哪几种?
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
定义法:对应边成比例,对应角相等的两个三角形相似.
三边成比例的两个三角形相似.
知识回顾
两角分别相等的两个三角形相似.
一组直角边和斜边成比例的两个直角三角形相似.
两边成比例且夹角相等的两个三角形相似.
相似三角形的判定方法有哪几种?
学习目标
1.理解并掌握相似三角形中对应线段的比等于相似比,并运用其解决问题.
2.理解相似三角形面积的比等于相似比的平方,并运用其解决问题.
课堂导入
三角形除了三个角,三条边外,还有哪些要素?
高
中线
角平分线
周长
面积
如果两个三角形相似,那么对应的这些要素有什么关系呢?
新知探究
知识点1:相似三角形对应线段的比
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
新知探究
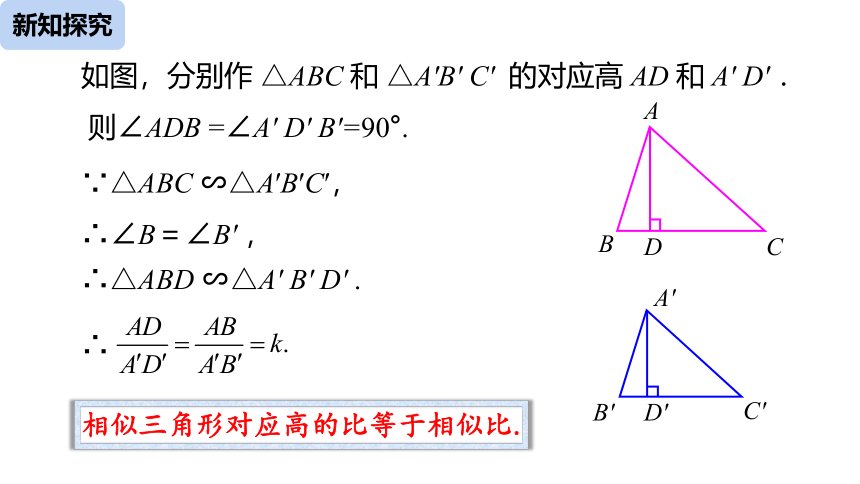
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
如图,分别作 △ABC 和 △A'B' C' 的对应高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
相似三角形对应高的比等于相似比.
新知探究
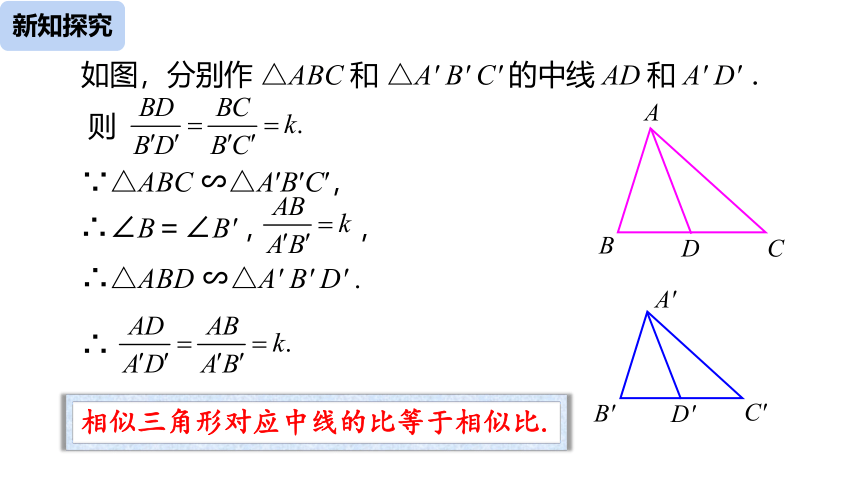
如图,分别作 △ABC 和 △A' B' C' 的中线 AD 和 A' D' .
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
则
∵△ABC ∽△A′B′C′,
相似三角形对应中线的比等于相似比.
∴∠B=∠B' , ,
新知探究
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
如图,分别作 △ABC 和 △A'B'C' 的角平分线 AD 和 A'D' .
则∠DAB =∠D'A'B'.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
相似三角形对应角平分线的比等于相似比.
新知探究
一般地,我们有:
相似三角形对应线段的比等于相似比.
在应用相似三角形对应线段的性质解题时,要注意并不是相似三角形中任意高的比、中线的比、角平分线的比都等于相似比,而是相似三角形中对应高的比、对应中线的比、对应角平分线的比等于相似比.
新知探究
相似三角形的周长比也等于相似比吗?为什么?
如果 △ABC ∽△A'B'C',相似比为 k,那么
因此 AB=k A'B',BC=kB'C',CA=kC'A',
从而
新知探究
相似三角形周长的性质:
相似三角形周长的比等于相似比.
跟踪训练
1.已知△ABC∽△DEF,且相似比为4:3,若△ABC 中 BC 边上的中线 AM =8,则△DEF 中 EF 边上的中线 DN 的长度为( )
A.3 B.4 C.5 D.6
D
????????????????=????????
?
本题源自《教材帮》
2.如图,在△ABC 中,两条中线 BE,CD 相交于点 O,则△EOD 的周长:△BOC的周长为( )
A.1:2 B.2:3
C.1:3 D.1:4
A
解析:∵BE,CD 是△ABC 的两条中线, ∴ DE 是△ABC 的中位线,
∴DE//BC,????????????????=12 ,∴△EOD∽△BOC,
∴△EOD 的周长:△BOC 的周长=1:2.
?
跟踪训练
本题源自《教材帮》
新知探究
知识点2:相似三角形面积的比
如图,△ABC ∽△A′B′C′,相似比为 k,它们的面积比是多少?
A
B
C
A'
B'
C'
新知探究
由前面的结论,我们有
A
B
C
A'
B'
C'
D'
D
新知探究
相似三角形面积的性质:
相似三角形面积的比等于相似比的平方.
相似三角形面积的比等于相似比的平方,不要与其周长的比等于相似比混淆.
新知探究
例3 如图,在△ABC 和△DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求△DEF 的边 EF 上的高和面积.
A
B
C
D
E
F
新知探究
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
解:在 △ABC 和 △DEF 中,∵ AB=2DE,AC=2DF,
又 ∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
∴
如图,在平行四边形 ABCD 中,点 E 是边 AD 的中点,连接 EC 交对角线 BD 于点 F,若 S△DEC=3,则S△BCF= .
跟踪训练
本题源自《教材帮》
解析:∵四边形 ABCD是平行四边形,∴AD//BC,AD =BC,
∴△DEF∽△BCF,∴????????????????=???????????????? .
∵点E是边 AD的中点, ∴DE=AE= 12AD= 12?BC,
∴ ????????????????=????????????????=12,∴ ????????????????=13 ,∴ ????△????????????????△????????????=????????????????=13.
又 S△DEC=3,∴S△DEF =1.
∵ ????△????????????????△????????????=????????????????2=14 ,∴ S△BCF=4.
?
跟踪训练
本题源自《教材帮》
①直接用面积公式;
②利用相似三角形的性质;
③利用等底或等高;
④割补法.
跟踪训练
解决面积问题的常用方法
随堂练习
1. 判断:
(1) 一个三角形的各边长扩大为原来的 5 倍,这个三角形的角平分线也扩大为原来的 5 倍. ( )
(2) 一个四边形的各边长扩大为原来的 9 倍,这个四边形的面积也扩大为原来的 9 倍. ( )
√
×
随堂练习
2.如果两个相似三角形的相似比是3:2,它们的周长差为8,那么较大的三角形的周长为 .
解析:设较大的三角形的周长为 x,
则较小的三角形的周长为 x-8.
∵这两个相似三角形的相似比为3 :2,
∴这两个三角形的周长比为 3:2.
∴ ?????????8=32 ,∴x=24.
?
24
本题源自《教材帮》
随堂练习
3.如图,在△ABC 中,DE//BC,AH⊥BC 于点 H,与 DE 交于点 G.若 ????????????????=35 ,则 ????????????????=, ????????????????=.
?
解析: ∵ DE//BC,∴△ADE ∽△ABC,
∴ ????????????????=????????????????=35 ,∴ ????????????????=32.
∵ DE//BC,
∴△ADG∽△ABH,∴ ????????????????=????????????????=35.
?
32
?
35
?
本题源自《教材帮》
课堂小结
相似三角形的性质
对应线段
周长
面积
等于相似比
对应高的比
对应中线的比
对应角平分线的比
周长的比等于相似比
面积的比等于相似比的平方
对接中考
1.(2019·沈阳中考)已知△ABC∽△ A'B'C' ,AD 和 A'D'是它们的对应中线,若 AD =10,A'D' =6,则△ABC 与△A'B'C' 的周长比是( )
A.3:5 B.9:25 C.5:3 D.25:9
解析: ∵△ABC∽△ A'B'C' ,AD 和A'D' 是它们的对应中线,AD=10, A'D' =6,∴△ABC 与△ A'B'C' 的相似比为 AD: A'D' =10:6=5:3,△ABC 与△ A'B'C' 的周长比为5:3.
C
本题源自《教材帮》
对接中考
2.(2019·巴中中考)如图,已知平行四边形 ABCD,F 为 BC 中点,延长 AD 至 E,使 DE:AD=1:3,连接 EF 交 DC 于点 G,则 S△DEG:S△CFG=( )
A.2:3 B.3:2
C.9:4 D.4:9
本题源自《教材帮》
对接中考
解析:设 DE=x,则 AD =3x.
∵ 四边形 ABCD 是平行四边形,
∴AD//BC,BC =AD =3x.
又点 F 是 BC 的中点, ∴ CF = 12BC= 32????.
∵ AD//BC,∴△DEG∽△CFG,
∴ ????△????????????????△????????????=????????????????2=????32????2=49.
?
本题源自《教材帮》
对接中考
解析:①当 AE:ED = 2:3时,AE:AD = 2:5.
∵ 四边形 ABCD 是平行四边形,
∴ AD//BC,AD = BC,
∴ AE:BC =2:5. ∵△AEF∽△CBF,
∴ S△AEF:S△CBF = 4:25.
3.(2019·凉山州中考)在平行四边形 ABCD 中,E 是AD 上一点,且点 E 将 AD 分为2:3的两部分,连接 BE,AC 相交于 F,则 S△AEF:S△CBF = .
对接中考
解析:②当 AE:ED = 3:2时,AE:AD = 3:5,
同理可得, S△AEF:S△CBF = 9:25.
4:25 或 9:25
3.(2019·凉山州中考)在平行四边形 ABCD 中,E 是AD 上一点,且点 E 将 AD 分为2:3的两部分,连接 BE,AC 相交于 F,则 S△AEF:S△CBF = .
注意AE:ED要分两种情况讨论.
课后作业
请完成课本后习题第6题.
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
27.2.2 相似三角形的性质
相 似
知识回顾
相似三角形的判定方法有哪几种?
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
定义法:对应边成比例,对应角相等的两个三角形相似.
三边成比例的两个三角形相似.
知识回顾
两角分别相等的两个三角形相似.
一组直角边和斜边成比例的两个直角三角形相似.
两边成比例且夹角相等的两个三角形相似.
相似三角形的判定方法有哪几种?
学习目标
1.理解并掌握相似三角形中对应线段的比等于相似比,并运用其解决问题.
2.理解相似三角形面积的比等于相似比的平方,并运用其解决问题.
课堂导入
三角形除了三个角,三条边外,还有哪些要素?
高
中线
角平分线
周长
面积
如果两个三角形相似,那么对应的这些要素有什么关系呢?
新知探究
知识点1:相似三角形对应线段的比
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
新知探究
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
如图,分别作 △ABC 和 △A'B' C' 的对应高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
相似三角形对应高的比等于相似比.
新知探究
如图,分别作 △ABC 和 △A' B' C' 的中线 AD 和 A' D' .
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
则
∵△ABC ∽△A′B′C′,
相似三角形对应中线的比等于相似比.
∴∠B=∠B' , ,
新知探究
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
如图,分别作 △ABC 和 △A'B'C' 的角平分线 AD 和 A'D' .
则∠DAB =∠D'A'B'.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
相似三角形对应角平分线的比等于相似比.
新知探究
一般地,我们有:
相似三角形对应线段的比等于相似比.
在应用相似三角形对应线段的性质解题时,要注意并不是相似三角形中任意高的比、中线的比、角平分线的比都等于相似比,而是相似三角形中对应高的比、对应中线的比、对应角平分线的比等于相似比.
新知探究
相似三角形的周长比也等于相似比吗?为什么?
如果 △ABC ∽△A'B'C',相似比为 k,那么
因此 AB=k A'B',BC=kB'C',CA=kC'A',
从而
新知探究
相似三角形周长的性质:
相似三角形周长的比等于相似比.
跟踪训练
1.已知△ABC∽△DEF,且相似比为4:3,若△ABC 中 BC 边上的中线 AM =8,则△DEF 中 EF 边上的中线 DN 的长度为( )
A.3 B.4 C.5 D.6
D
????????????????=????????
?
本题源自《教材帮》
2.如图,在△ABC 中,两条中线 BE,CD 相交于点 O,则△EOD 的周长:△BOC的周长为( )
A.1:2 B.2:3
C.1:3 D.1:4
A
解析:∵BE,CD 是△ABC 的两条中线, ∴ DE 是△ABC 的中位线,
∴DE//BC,????????????????=12 ,∴△EOD∽△BOC,
∴△EOD 的周长:△BOC 的周长=1:2.
?
跟踪训练
本题源自《教材帮》
新知探究
知识点2:相似三角形面积的比
如图,△ABC ∽△A′B′C′,相似比为 k,它们的面积比是多少?
A
B
C
A'
B'
C'
新知探究
由前面的结论,我们有
A
B
C
A'
B'
C'
D'
D
新知探究
相似三角形面积的性质:
相似三角形面积的比等于相似比的平方.
相似三角形面积的比等于相似比的平方,不要与其周长的比等于相似比混淆.
新知探究
例3 如图,在△ABC 和△DEF 中,AB = 2 DE ,AC = 2 DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求△DEF 的边 EF 上的高和面积.
A
B
C
D
E
F
新知探究
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
解:在 △ABC 和 △DEF 中,∵ AB=2DE,AC=2DF,
又 ∵∠D=∠A,
∴ △DEF ∽ △ABC ,相似比为 1 : 2.
∴
如图,在平行四边形 ABCD 中,点 E 是边 AD 的中点,连接 EC 交对角线 BD 于点 F,若 S△DEC=3,则S△BCF= .
跟踪训练
本题源自《教材帮》
解析:∵四边形 ABCD是平行四边形,∴AD//BC,AD =BC,
∴△DEF∽△BCF,∴????????????????=???????????????? .
∵点E是边 AD的中点, ∴DE=AE= 12AD= 12?BC,
∴ ????????????????=????????????????=12,∴ ????????????????=13 ,∴ ????△????????????????△????????????=????????????????=13.
又 S△DEC=3,∴S△DEF =1.
∵ ????△????????????????△????????????=????????????????2=14 ,∴ S△BCF=4.
?
跟踪训练
本题源自《教材帮》
①直接用面积公式;
②利用相似三角形的性质;
③利用等底或等高;
④割补法.
跟踪训练
解决面积问题的常用方法
随堂练习
1. 判断:
(1) 一个三角形的各边长扩大为原来的 5 倍,这个三角形的角平分线也扩大为原来的 5 倍. ( )
(2) 一个四边形的各边长扩大为原来的 9 倍,这个四边形的面积也扩大为原来的 9 倍. ( )
√
×
随堂练习
2.如果两个相似三角形的相似比是3:2,它们的周长差为8,那么较大的三角形的周长为 .
解析:设较大的三角形的周长为 x,
则较小的三角形的周长为 x-8.
∵这两个相似三角形的相似比为3 :2,
∴这两个三角形的周长比为 3:2.
∴ ?????????8=32 ,∴x=24.
?
24
本题源自《教材帮》
随堂练习
3.如图,在△ABC 中,DE//BC,AH⊥BC 于点 H,与 DE 交于点 G.若 ????????????????=35 ,则 ????????????????=, ????????????????=.
?
解析: ∵ DE//BC,∴△ADE ∽△ABC,
∴ ????????????????=????????????????=35 ,∴ ????????????????=32.
∵ DE//BC,
∴△ADG∽△ABH,∴ ????????????????=????????????????=35.
?
32
?
35
?
本题源自《教材帮》
课堂小结
相似三角形的性质
对应线段
周长
面积
等于相似比
对应高的比
对应中线的比
对应角平分线的比
周长的比等于相似比
面积的比等于相似比的平方
对接中考
1.(2019·沈阳中考)已知△ABC∽△ A'B'C' ,AD 和 A'D'是它们的对应中线,若 AD =10,A'D' =6,则△ABC 与△A'B'C' 的周长比是( )
A.3:5 B.9:25 C.5:3 D.25:9
解析: ∵△ABC∽△ A'B'C' ,AD 和A'D' 是它们的对应中线,AD=10, A'D' =6,∴△ABC 与△ A'B'C' 的相似比为 AD: A'D' =10:6=5:3,△ABC 与△ A'B'C' 的周长比为5:3.
C
本题源自《教材帮》
对接中考
2.(2019·巴中中考)如图,已知平行四边形 ABCD,F 为 BC 中点,延长 AD 至 E,使 DE:AD=1:3,连接 EF 交 DC 于点 G,则 S△DEG:S△CFG=( )
A.2:3 B.3:2
C.9:4 D.4:9
本题源自《教材帮》
对接中考
解析:设 DE=x,则 AD =3x.
∵ 四边形 ABCD 是平行四边形,
∴AD//BC,BC =AD =3x.
又点 F 是 BC 的中点, ∴ CF = 12BC= 32????.
∵ AD//BC,∴△DEG∽△CFG,
∴ ????△????????????????△????????????=????????????????2=????32????2=49.
?
本题源自《教材帮》
对接中考
解析:①当 AE:ED = 2:3时,AE:AD = 2:5.
∵ 四边形 ABCD 是平行四边形,
∴ AD//BC,AD = BC,
∴ AE:BC =2:5. ∵△AEF∽△CBF,
∴ S△AEF:S△CBF = 4:25.
3.(2019·凉山州中考)在平行四边形 ABCD 中,E 是AD 上一点,且点 E 将 AD 分为2:3的两部分,连接 BE,AC 相交于 F,则 S△AEF:S△CBF = .
对接中考
解析:②当 AE:ED = 3:2时,AE:AD = 3:5,
同理可得, S△AEF:S△CBF = 9:25.
4:25 或 9:25
3.(2019·凉山州中考)在平行四边形 ABCD 中,E 是AD 上一点,且点 E 将 AD 分为2:3的两部分,连接 BE,AC 相交于 F,则 S△AEF:S△CBF = .
注意AE:ED要分两种情况讨论.
课后作业
请完成课本后习题第6题.
