人教版数学九年级下册27.2.1 相似三角形的判定 课时2课件(23张)
文档属性
| 名称 | 人教版数学九年级下册27.2.1 相似三角形的判定 课时2课件(23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 543.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览



文档简介
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
27.2.1 相似三角形的判定
相 似
知识回顾
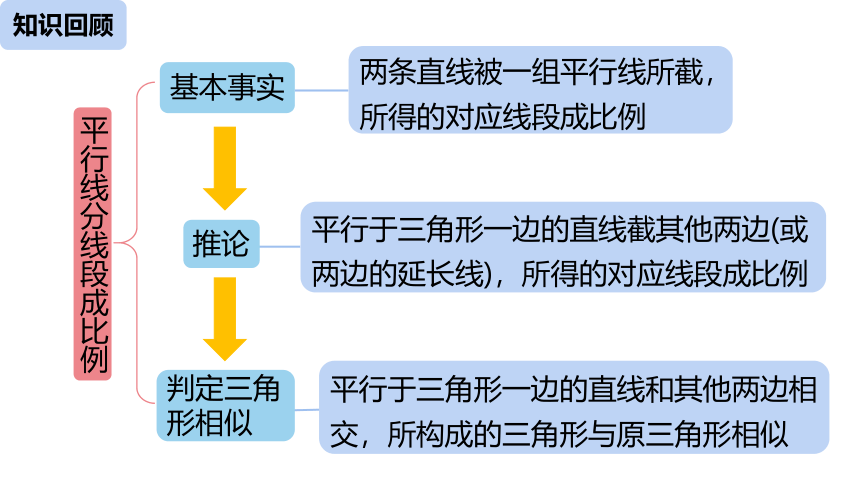
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例
平行线分线段成比例
基本事实
推论
判定三角形相似
两条直线被一组平行线所截,所得的对应线段成比例
学习目标
2.掌握利用三边来判定两个三角形相似的方法,并能进行相关计算.
1.复习已经学过的三角形相似的判定定理.
课堂导入
A
B
C
D
E
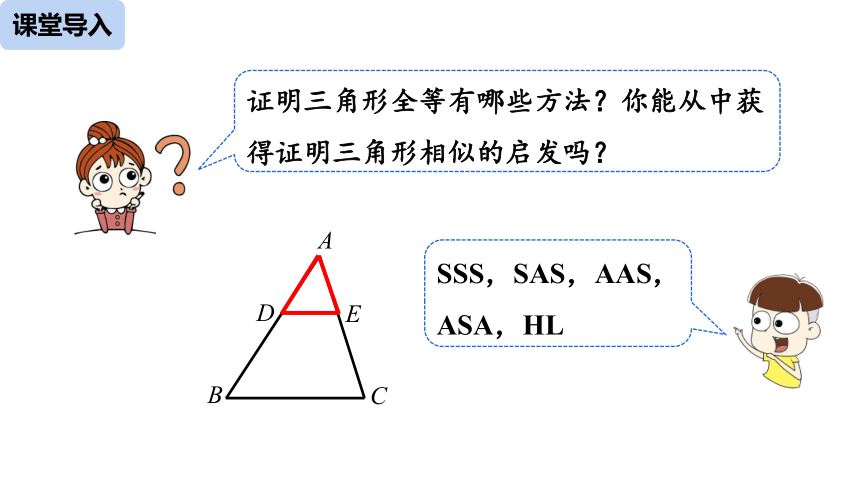
证明三角形全等有哪些方法?你能从中获得证明三角形相似的启发吗?
SSS,SAS,AAS,ASA,HL
课堂导入
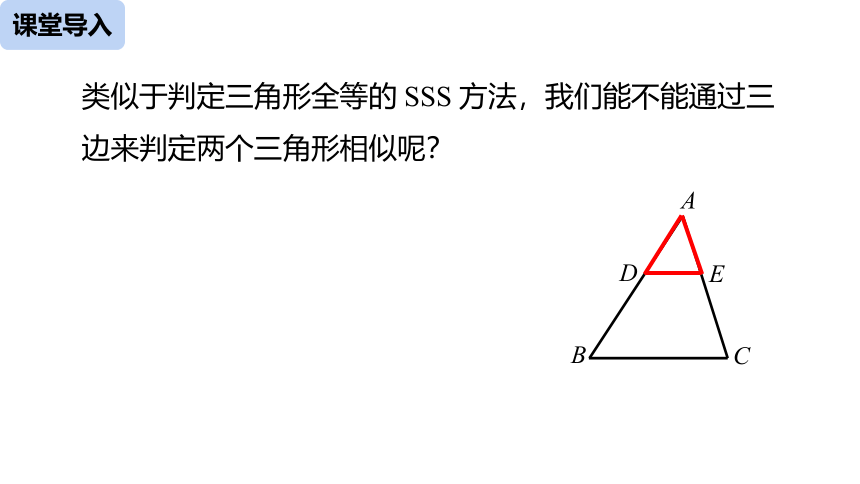
类似于判定三角形全等的 SSS 方法,我们能不能通过三边来判定两个三角形相似呢?
A
B
C
D
E
新知探究
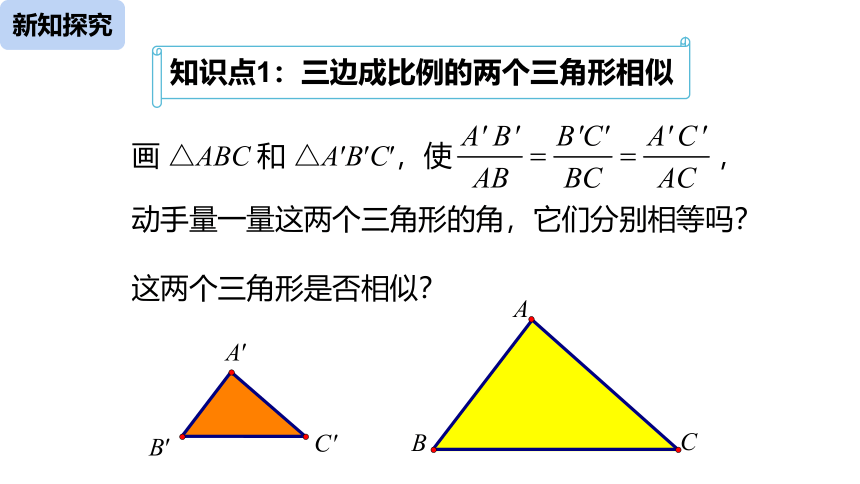
知识点1:三边成比例的两个三角形相似
画 △ABC 和 △A′B′C′,使 ,
动手量一量这两个三角形的角,它们分别相等吗?这两个三角形是否相似?
A
B
C
C′
B′
A′
新知探究
A
B
C
C′
B′
A′
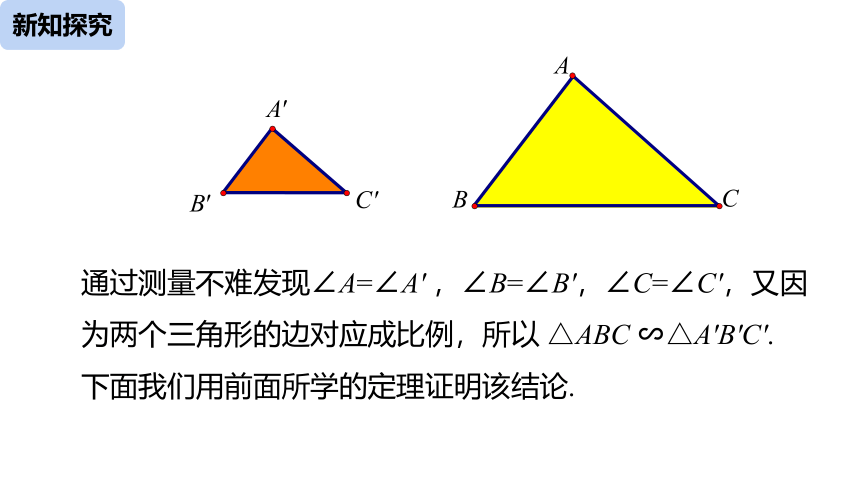
通过测量不难发现∠A=∠A' ,∠B=∠B',∠C=∠C',又因为两个三角形的边对应成比例,所以 △ABC ∽△A′B′C′. 下面我们用前面所学的定理证明该结论.
新知探究
∴
C′
B′
A′
证明:在线段 AB (或延长线) 上截取 AD=A′B′,
过点 D 作 DE∥BC ,交AC于点 E.
∵ DE∥BC ,∴ △ADE ∽ △ABC.
∴ DE=B′C′,EA=C′A′.
∴△ADE≌△A′B′C′,△A′B′C′ ∽△ABC.
B
C
A
D
E
又 ,AD=A′B′,
∴ , .
新知探究
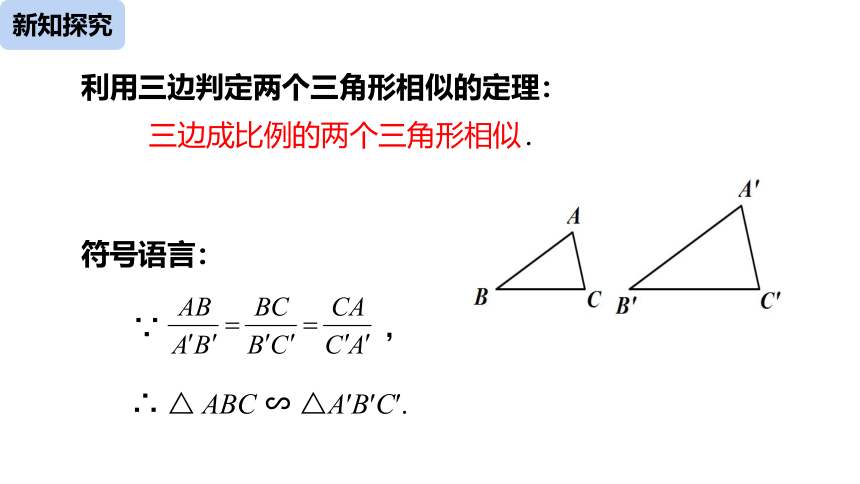
利用三边判定两个三角形相似的定理:
三边成比例的两个三角形相似.
∵ ,
∴ △ ABC ∽ △A′B′C′.
符号语言:
新知探究
利用三边成比例判定两个三角形相似时,一定要注意边与边之间的对应关系,主要根据最长边与最长边对应,最短边与最短边对应的思路找对应边.
新知探究
利用三边成比例判定两个三角形是否相似的步骤
(1)排序:将两个三角形的边长分别按从小到大(或从大到小)的顺序排列;
(2)计算:计算最长边与最长边、最短边与最短边、第三边与第三边的比值;
(3)判断:若比值相等,则这两个三角形相似.
1.已知 △ABC 和 △DEF,根据下列条件判断它们是否相似.
(3) AB=12, BC=15, AC=24,
DE=16,EF=20, DF=30.
(2) AB=4, BC=8, AC=10,
DE=20,EF=16, DF=8;
(1) AB=3, BC=4, AC=6,
DE=6, EF=8, DF=9;
是
否
否
跟踪训练
2.图中每个小方格都是边长为1的正方形,若 A,B,C,D,E,F 都是格点,试说明 △ABC ∽△DEF.
解:因为 AC= 2,BC= 12+32=10,
AB=4,DF= 22+22=22 ,
EF= 22+62=210 ,ED=8,
∴????????????????=????????????????=????????????????=12 ,
∴△ABC∽△DEF.
?
跟踪训练
1.如图,∠APD=90°,AP=PB=BC=CD,下列结论正确的是( )
A. △PAB∽△PCA
B. △PAB∽△PDA
C. △ABC∽△DBA
D. △ABC∽△DCA
A
C
B
P
D
C
解析:设AP=PB=BC=CD=a,∵∠APD=90°,∴AB= ,AC= ,AD= . ∵ AB : BC = BD : AB = AD : AC,∴△ABC∽△DBA,故选C.
随堂练习
随堂练习
2.如图,△ABC 与 △DEF 相似吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
A
C
B
D
E
F
????
?
4
????????
?
8
????????????
?
????????
?
相似
随堂练习
3.如图,在 Rt△ABC 与 Rt△A′B′C′中,∠C =∠C'= 90°,且 求证:△ A′B′C′∽△ABC.
随堂练习
证明:由已知条件得 AB = 2 A′B′,AC = 2 A′C′,
∴ △ A′B′C′∽△ABC.
∴ BC=2B′C′,
∴ BC 2 = AB 2-AC 2 = ( 2 A′B′ )2-( 2 A′C′ )2
= 4 A′B′ 2- 4 A′C′ 2 = 4 ( A′B′ 2-A′C′ 2 )
= 4 B′C′ 2 = ( 2 B′C′ )2.
三边对应成比例的两个三角形相似.
随堂练习
4.如图,△ABC中,点 D,E,F 分别是 AB,BC,CA 的中点,求证:△ABC∽△EFD.
∴ △ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,
CA的中点,
∴
∴
三边成比例的两个三角形相似.
课堂小结
三边成比例的两三角形相似
定理
步骤
排序
计算
判断
对接中考
1.(2019·雅安中考)如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1 相似的是( )
边长分别为
2,????,????????
?
B
边长分别为3,????,????
?
边长分别为
1,????,2????
?
边长分别为1,????,????
?
边长分别为
2,????,????????
?
对接中考
2.(2015·梅州中考)已知△ABC 中,点 E 是 AB 边的中点,点 F 在 AC 边上,若以 A,E,F 为顶点的三角形与△ABC 相似,则需要增加的一个条件是___________________.(写出一个条件即可)
点 F 是 AC 边的中点
F
E
A
B
C
中位线
????????????????=????????????????=????????????????=????????
?
△AEF∽△ABC
对接中考
3.(2020·昆明中考)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC 是格点三角形,在图中的 6×6 正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE 只算一个),这样的格点三角形一共有( )
A.4个
B.5个
C.6个
D.7个
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
B
A
C
C
课后作业
请完成课本后习题第1题.
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
27.2.1 相似三角形的判定
相 似
知识回顾
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例
平行线分线段成比例
基本事实
推论
判定三角形相似
两条直线被一组平行线所截,所得的对应线段成比例
学习目标
2.掌握利用三边来判定两个三角形相似的方法,并能进行相关计算.
1.复习已经学过的三角形相似的判定定理.
课堂导入
A
B
C
D
E
证明三角形全等有哪些方法?你能从中获得证明三角形相似的启发吗?
SSS,SAS,AAS,ASA,HL
课堂导入
类似于判定三角形全等的 SSS 方法,我们能不能通过三边来判定两个三角形相似呢?
A
B
C
D
E
新知探究
知识点1:三边成比例的两个三角形相似
画 △ABC 和 △A′B′C′,使 ,
动手量一量这两个三角形的角,它们分别相等吗?这两个三角形是否相似?
A
B
C
C′
B′
A′
新知探究
A
B
C
C′
B′
A′
通过测量不难发现∠A=∠A' ,∠B=∠B',∠C=∠C',又因为两个三角形的边对应成比例,所以 △ABC ∽△A′B′C′. 下面我们用前面所学的定理证明该结论.
新知探究
∴
C′
B′
A′
证明:在线段 AB (或延长线) 上截取 AD=A′B′,
过点 D 作 DE∥BC ,交AC于点 E.
∵ DE∥BC ,∴ △ADE ∽ △ABC.
∴ DE=B′C′,EA=C′A′.
∴△ADE≌△A′B′C′,△A′B′C′ ∽△ABC.
B
C
A
D
E
又 ,AD=A′B′,
∴ , .
新知探究
利用三边判定两个三角形相似的定理:
三边成比例的两个三角形相似.
∵ ,
∴ △ ABC ∽ △A′B′C′.
符号语言:
新知探究
利用三边成比例判定两个三角形相似时,一定要注意边与边之间的对应关系,主要根据最长边与最长边对应,最短边与最短边对应的思路找对应边.
新知探究
利用三边成比例判定两个三角形是否相似的步骤
(1)排序:将两个三角形的边长分别按从小到大(或从大到小)的顺序排列;
(2)计算:计算最长边与最长边、最短边与最短边、第三边与第三边的比值;
(3)判断:若比值相等,则这两个三角形相似.
1.已知 △ABC 和 △DEF,根据下列条件判断它们是否相似.
(3) AB=12, BC=15, AC=24,
DE=16,EF=20, DF=30.
(2) AB=4, BC=8, AC=10,
DE=20,EF=16, DF=8;
(1) AB=3, BC=4, AC=6,
DE=6, EF=8, DF=9;
是
否
否
跟踪训练
2.图中每个小方格都是边长为1的正方形,若 A,B,C,D,E,F 都是格点,试说明 △ABC ∽△DEF.
解:因为 AC= 2,BC= 12+32=10,
AB=4,DF= 22+22=22 ,
EF= 22+62=210 ,ED=8,
∴????????????????=????????????????=????????????????=12 ,
∴△ABC∽△DEF.
?
跟踪训练
1.如图,∠APD=90°,AP=PB=BC=CD,下列结论正确的是( )
A. △PAB∽△PCA
B. △PAB∽△PDA
C. △ABC∽△DBA
D. △ABC∽△DCA
A
C
B
P
D
C
解析:设AP=PB=BC=CD=a,∵∠APD=90°,∴AB= ,AC= ,AD= . ∵ AB : BC = BD : AB = AD : AC,∴△ABC∽△DBA,故选C.
随堂练习
随堂练习
2.如图,△ABC 与 △DEF 相似吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
A
C
B
D
E
F
????
?
4
????????
?
8
????????????
?
????????
?
相似
随堂练习
3.如图,在 Rt△ABC 与 Rt△A′B′C′中,∠C =∠C'= 90°,且 求证:△ A′B′C′∽△ABC.
随堂练习
证明:由已知条件得 AB = 2 A′B′,AC = 2 A′C′,
∴ △ A′B′C′∽△ABC.
∴ BC=2B′C′,
∴ BC 2 = AB 2-AC 2 = ( 2 A′B′ )2-( 2 A′C′ )2
= 4 A′B′ 2- 4 A′C′ 2 = 4 ( A′B′ 2-A′C′ 2 )
= 4 B′C′ 2 = ( 2 B′C′ )2.
三边对应成比例的两个三角形相似.
随堂练习
4.如图,△ABC中,点 D,E,F 分别是 AB,BC,CA 的中点,求证:△ABC∽△EFD.
∴ △ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,
CA的中点,
∴
∴
三边成比例的两个三角形相似.
课堂小结
三边成比例的两三角形相似
定理
步骤
排序
计算
判断
对接中考
1.(2019·雅安中考)如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1 相似的是( )
边长分别为
2,????,????????
?
B
边长分别为3,????,????
?
边长分别为
1,????,2????
?
边长分别为1,????,????
?
边长分别为
2,????,????????
?
对接中考
2.(2015·梅州中考)已知△ABC 中,点 E 是 AB 边的中点,点 F 在 AC 边上,若以 A,E,F 为顶点的三角形与△ABC 相似,则需要增加的一个条件是___________________.(写出一个条件即可)
点 F 是 AC 边的中点
F
E
A
B
C
中位线
????????????????=????????????????=????????????????=????????
?
△AEF∽△ABC
对接中考
3.(2020·昆明中考)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC 是格点三角形,在图中的 6×6 正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE 只算一个),这样的格点三角形一共有( )
A.4个
B.5个
C.6个
D.7个
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
B
A
C
C
课后作业
请完成课本后习题第1题.
