人教版数学九年级下册27.1图形的相似 课时1课件(31张)
文档属性
| 名称 | 人教版数学九年级下册27.1图形的相似 课时1课件(31张) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 22:02:36 | ||
图片预览










文档简介
27.1 图形的相似
相 似
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
形状相同,大小也相同.
什么样的图形是全等形?
学习目标
1.能通过生活中的实例认识图形的相似,通过观察直观地判断两个图形是否相似.
2.了解成比例线段的概念.
课堂导入
全等!
下图中的两个图形有什么关系?
课堂导入
大小不同,不全等!
如果把其中的一片树叶缩小,它们还全等吗?
新知探究
知识点1:相似图形
下面的每组图形有什么相同和不同的地方?
新知探究
我们把形状相同的图形叫相似图形.
定义:
两个图形是否相似与图形的大小、位置无关.
相同点:形状相同
不同点:大小不同
活学巧记
相似图形形状同,大小位置均无关;
相似图形有特例,全等属于相似形.
新知探究
1. 图形的放大:
相似图形的关系:
新知探究
相似图形的关系:
2. 图形的缩小:
新知探究
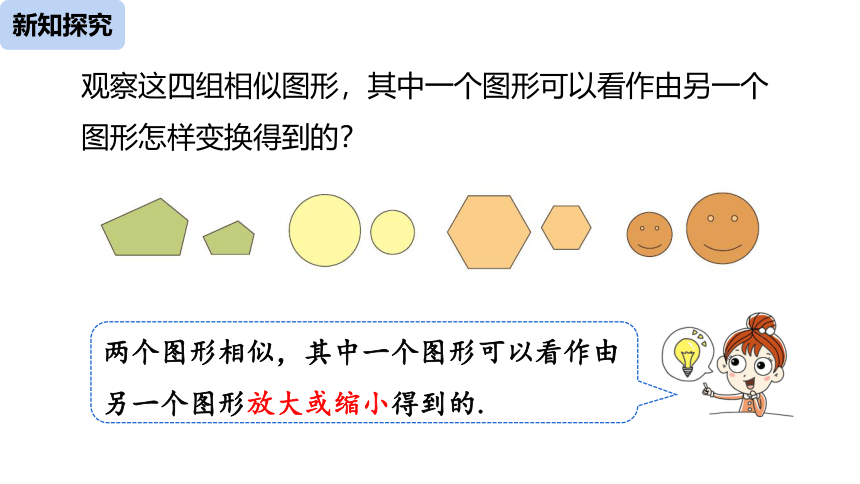
观察这四组相似图形,其中一个图形可以看作由另一个图形怎样变换得到的?
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到的.
新知探究
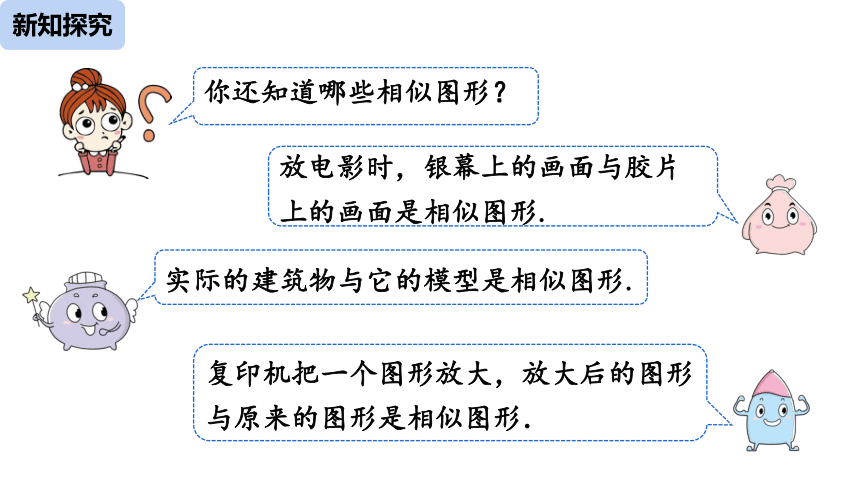
你还知道哪些相似图形?
放电影时,银幕上的画面与胶片上的画面是相似图形.
复印机把一个图形放大,放大后的图形与原来的图形是相似图形.
实际的建筑物与它的模型是相似图形.
新知探究
国旗上的大五角星与小五角星是相似图形吗?四颗小五角星呢?
全等图形是特殊的相似图形,也就是说全等图形一定是相似图形,但相似图形不一定是全等图形.
新知探究
如图是一个女孩从平面镜和哈哈镜里看到的自己的形象,这些镜中的形象与自身相似吗?
拉长
压扁
相似
判断两个图形是否相似,就是看这两个图形的形状是否相同,这是相似图形的本质.
跟踪训练
1.如图,从放大镜里看到的三角尺和原来的三角尺相似吗?
2.如图,图形( a )~( f )中,哪些与图形(1)或(2)相似?
跟踪训练
新知探究
知识点2:成比例线段
1.线段的比:在同一长度单位下,量得的两条线段长度的比叫做这两条线段的比.
(1)线段的比是线段长度的比,是两条线段长度的比的运算结果,是一个没有单位的正数.
(2)线段的比与所选线段的长度单位无关,在求两条线段的比时,要求两条线段的长度单位必须一致.
新知探究
2.四条线段成比例:对于四条线段 a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等.如 ????????=???????? (即 ad = bc).我们就说这四条线段成比例.
?
(1)成比例线段是有顺序的,即若 a,b,c,d 是成比例线段,则 ????????=???????? (或ad = bc),不能写成 ????????=????????.
(2)在运用 ????????=???????? 运算时,通常情况下,四条线段 a,b,c,d 的长度单位要一致,但有时为了计算方便,a,b 的长度单位一致,c,d 的长度单位一致也可以.
?
新知探究
(1)基本性质:若 ????????=???????? ,则 ad=bc.
(2)合比性质:若 ????????=???????? ,则 ????+????????=????+????????.
(3)分比性质:若 ????????=???????? ,则 ?????????????=?????????????.
(4)等比性质:若 ????????=????????=?=????????
(b+d+…+n≠0),则 ????+????+?+????????+????+?+????=????????.
?
比例的相关性质
1.下列各组中的四条线段成比例的是( )
A.6 cm,2 cm,1 cm,4 cm
B.4 cm,5 cm,6 cm,7 cm
C.3 cm,4 cm,5 cm,6 cm
D.6 cm,3 cm,8 cm,4 cm
D
1×6≠2×4
4×7≠5×6
3×6≠4×5
3×8=4×6
跟踪训练
判断四条线段是否成比例的方法
首先统一单位,并把四条线段按从小到大(或从大到小)的顺序排列,然后计算并判断.计算的方法有两种:
(1)计算前两条线段的比和后两条线段的比,若比值相等,则这四条线段成比例;
(2)计算第一条线段与第四条线段的乘积、第二条线段与第三条线段的乘积,如果乘积相同,则这四条线段成比例.
跟踪训练
2.某市的两个旅游景区之间的距离为 105 km,则在一张比例尺为 1:2000000 的交通旅游图上,它们之间的距离大约相当于( )
A.一根火柴的长度
B.一支钢笔的长度
C.一支铅笔的长度
D.一根筷子的长度
10500000 cm
x:10500000=1:12000000
A
列式时,图上距离和实际距离的单位要统一.
跟踪训练
随堂练习
1.下列图形中,不是相似图形的是( )
C
随堂练习
2.下列图形中一定是相似图形的是( )
A.两个等边三角形
B.两个菱形
C.两个矩形
D.两个直角三角形
A
随堂练习
3.若????5=????8,则?????????????等于( )
A. 35 B.53 C. 85 D. 58
?
解析:∵????5=????8,
∴????=58????,则 ?????????????=?????58????58????=35 .
?
A
还有其他解法吗?
随堂练习
3.若????5=????8,则?????????????等于( )
A. 35 B.53 C. 85 D. 58
?
解析:∵????5=????8,
∴ 不妨设 ????5=????8=????,则 a=5k,b=8k,
∴则 ?????????????=8?????5????5????=35 .
?
A
还可以采用参数法!
随堂练习
利用比例的性质求代数式的值的方法
(1)用含有一个字母的代数式表示其他字母,然后代入求值;
(2)参数法,即先根据比例式设出合适的参数,然后用含此参数的代数式表示出相应的字母,再代入求值.
课堂小结
图形的相似
相似图形的概念
成比例线段
线段的比
四条线段成比例
对接中考
1.(2013·莆田中考)下列四组图形中,一定相似的是( )
A.正方形与矩形
B.正方形与菱形
C.菱形与菱形
D.正五边形与正五边形
D
对接中考
2.(2019·郴州中考)若 ????+????????=32 ,则 ????????=.
?
2(x+y) = 3x?x = 2y
?
12
?
对接中考
3.(2017·娄底中考)湖南地图出版社首发的竖版《中华人民共和国地图》,将南海诸岛与大陆按同比例尺1:6700000表示出来,使读者能够全面、直观地认识我国版图.若在这种地图上量得我国南北的图上距离是82.09 厘米,则我国南北的实际距离大约是 千米(结果精确到1千米).
5500
82.09×6700000=550003000(cm)≈5500(km)
课后作业
请完成课本后习题第1、2题.
相 似
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
形状相同,大小也相同.
什么样的图形是全等形?
学习目标
1.能通过生活中的实例认识图形的相似,通过观察直观地判断两个图形是否相似.
2.了解成比例线段的概念.
课堂导入
全等!
下图中的两个图形有什么关系?
课堂导入
大小不同,不全等!
如果把其中的一片树叶缩小,它们还全等吗?
新知探究
知识点1:相似图形
下面的每组图形有什么相同和不同的地方?
新知探究
我们把形状相同的图形叫相似图形.
定义:
两个图形是否相似与图形的大小、位置无关.
相同点:形状相同
不同点:大小不同
活学巧记
相似图形形状同,大小位置均无关;
相似图形有特例,全等属于相似形.
新知探究
1. 图形的放大:
相似图形的关系:
新知探究
相似图形的关系:
2. 图形的缩小:
新知探究
观察这四组相似图形,其中一个图形可以看作由另一个图形怎样变换得到的?
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到的.
新知探究
你还知道哪些相似图形?
放电影时,银幕上的画面与胶片上的画面是相似图形.
复印机把一个图形放大,放大后的图形与原来的图形是相似图形.
实际的建筑物与它的模型是相似图形.
新知探究
国旗上的大五角星与小五角星是相似图形吗?四颗小五角星呢?
全等图形是特殊的相似图形,也就是说全等图形一定是相似图形,但相似图形不一定是全等图形.
新知探究
如图是一个女孩从平面镜和哈哈镜里看到的自己的形象,这些镜中的形象与自身相似吗?
拉长
压扁
相似
判断两个图形是否相似,就是看这两个图形的形状是否相同,这是相似图形的本质.
跟踪训练
1.如图,从放大镜里看到的三角尺和原来的三角尺相似吗?
2.如图,图形( a )~( f )中,哪些与图形(1)或(2)相似?
跟踪训练
新知探究
知识点2:成比例线段
1.线段的比:在同一长度单位下,量得的两条线段长度的比叫做这两条线段的比.
(1)线段的比是线段长度的比,是两条线段长度的比的运算结果,是一个没有单位的正数.
(2)线段的比与所选线段的长度单位无关,在求两条线段的比时,要求两条线段的长度单位必须一致.
新知探究
2.四条线段成比例:对于四条线段 a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等.如 ????????=???????? (即 ad = bc).我们就说这四条线段成比例.
?
(1)成比例线段是有顺序的,即若 a,b,c,d 是成比例线段,则 ????????=???????? (或ad = bc),不能写成 ????????=????????.
(2)在运用 ????????=???????? 运算时,通常情况下,四条线段 a,b,c,d 的长度单位要一致,但有时为了计算方便,a,b 的长度单位一致,c,d 的长度单位一致也可以.
?
新知探究
(1)基本性质:若 ????????=???????? ,则 ad=bc.
(2)合比性质:若 ????????=???????? ,则 ????+????????=????+????????.
(3)分比性质:若 ????????=???????? ,则 ?????????????=?????????????.
(4)等比性质:若 ????????=????????=?=????????
(b+d+…+n≠0),则 ????+????+?+????????+????+?+????=????????.
?
比例的相关性质
1.下列各组中的四条线段成比例的是( )
A.6 cm,2 cm,1 cm,4 cm
B.4 cm,5 cm,6 cm,7 cm
C.3 cm,4 cm,5 cm,6 cm
D.6 cm,3 cm,8 cm,4 cm
D
1×6≠2×4
4×7≠5×6
3×6≠4×5
3×8=4×6
跟踪训练
判断四条线段是否成比例的方法
首先统一单位,并把四条线段按从小到大(或从大到小)的顺序排列,然后计算并判断.计算的方法有两种:
(1)计算前两条线段的比和后两条线段的比,若比值相等,则这四条线段成比例;
(2)计算第一条线段与第四条线段的乘积、第二条线段与第三条线段的乘积,如果乘积相同,则这四条线段成比例.
跟踪训练
2.某市的两个旅游景区之间的距离为 105 km,则在一张比例尺为 1:2000000 的交通旅游图上,它们之间的距离大约相当于( )
A.一根火柴的长度
B.一支钢笔的长度
C.一支铅笔的长度
D.一根筷子的长度
10500000 cm
x:10500000=1:12000000
A
列式时,图上距离和实际距离的单位要统一.
跟踪训练
随堂练习
1.下列图形中,不是相似图形的是( )
C
随堂练习
2.下列图形中一定是相似图形的是( )
A.两个等边三角形
B.两个菱形
C.两个矩形
D.两个直角三角形
A
随堂练习
3.若????5=????8,则?????????????等于( )
A. 35 B.53 C. 85 D. 58
?
解析:∵????5=????8,
∴????=58????,则 ?????????????=?????58????58????=35 .
?
A
还有其他解法吗?
随堂练习
3.若????5=????8,则?????????????等于( )
A. 35 B.53 C. 85 D. 58
?
解析:∵????5=????8,
∴ 不妨设 ????5=????8=????,则 a=5k,b=8k,
∴则 ?????????????=8?????5????5????=35 .
?
A
还可以采用参数法!
随堂练习
利用比例的性质求代数式的值的方法
(1)用含有一个字母的代数式表示其他字母,然后代入求值;
(2)参数法,即先根据比例式设出合适的参数,然后用含此参数的代数式表示出相应的字母,再代入求值.
课堂小结
图形的相似
相似图形的概念
成比例线段
线段的比
四条线段成比例
对接中考
1.(2013·莆田中考)下列四组图形中,一定相似的是( )
A.正方形与矩形
B.正方形与菱形
C.菱形与菱形
D.正五边形与正五边形
D
对接中考
2.(2019·郴州中考)若 ????+????????=32 ,则 ????????=.
?
2(x+y) = 3x?x = 2y
?
12
?
对接中考
3.(2017·娄底中考)湖南地图出版社首发的竖版《中华人民共和国地图》,将南海诸岛与大陆按同比例尺1:6700000表示出来,使读者能够全面、直观地认识我国版图.若在这种地图上量得我国南北的图上距离是82.09 厘米,则我国南北的实际距离大约是 千米(结果精确到1千米).
5500
82.09×6700000=550003000(cm)≈5500(km)
课后作业
请完成课本后习题第1、2题.
