人教版数学九年级下册27.3 位似 课时2课件(31张)
文档属性
| 名称 | 人教版数学九年级下册27.3 位似 课时2课件(31张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览








文档简介
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
27.3 位似
相 似
知识回顾
两个相似多边形,如果它们对应顶点所在的直线相交于一点,我们就把这样的两个图形叫做位似图形.
位似图形的概念是什么?
学习目标
1.理解平面直角坐标系中,位似图形对应点的坐标之间的联系.
2.会用图形的坐标的变化表示图形的位似变换,掌握把一个图形按一定比例放大或缩小后,点的坐标变化的规律.
3.了解四种图形变换 (平移、轴对称、旋转和位似) 的异同,并能在复杂图形中找出来这些变换.
课堂导入
我们知道,在直角坐标系中,可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、轴对称和旋转 (中心对称). 那么,位似是否也可以用两个图形坐标之间的关系来表示呢?
新知探究
知识点1:平面直角坐标系中的位似变换
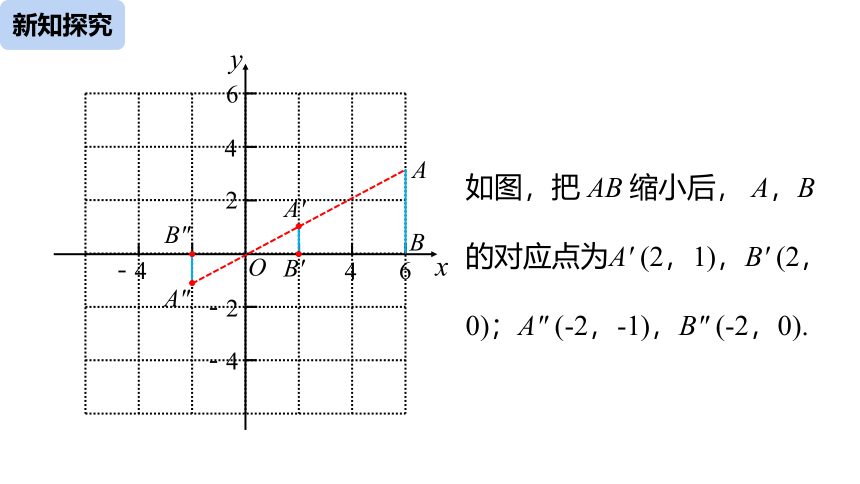
在平面直角坐标系中,有两点 A (6,3),B (6,0).以原点 O 为位似中心,相似比为 ,把线段 AB 缩小.
观察对应点之间坐标有什么变化.
新知探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
6
4
6
B'
-2
-4
-4
x
y
A
B
A'
A"
B"
O
如图,把 AB 缩小后, A,B 的对应点为A′ (2,1),B′ (2,0);A" (-2,-1),B" (-2,0).
新知探究
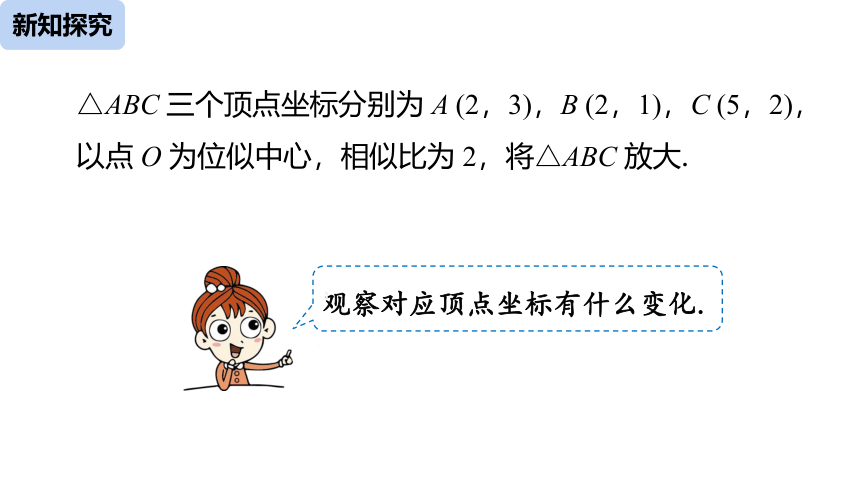
△ABC 三个顶点坐标分别为 A (2,3),B (2,1),C (5,2),以点 O 为位似中心,相似比为 2,将△ABC 放大.
观察对应顶点坐标有什么变化.
新知探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-6
B'
A'
C'
A"
B"
C"
如图,把 △ABC 放大后 A,B,C 的对应点为A' (4,6),B' (4,2),C' (10,4);A" (-4,-6),B" (-4,-2),C" (-10,-4).
O
新知探究
在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
两个.
新知探究
所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
当位似图形在原点同侧时,其对应顶点的坐标的比为 k;当位似图形在原点两侧时,其对应顶点的坐标的比为 -k.
新知探究
平面直角坐标系中位似变换坐标的变化规律:一般地,在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为 k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
上面的坐标的变化规律是以原点为位似中心的位似变换中图形上对应点的坐标的变化规律.
新知探究
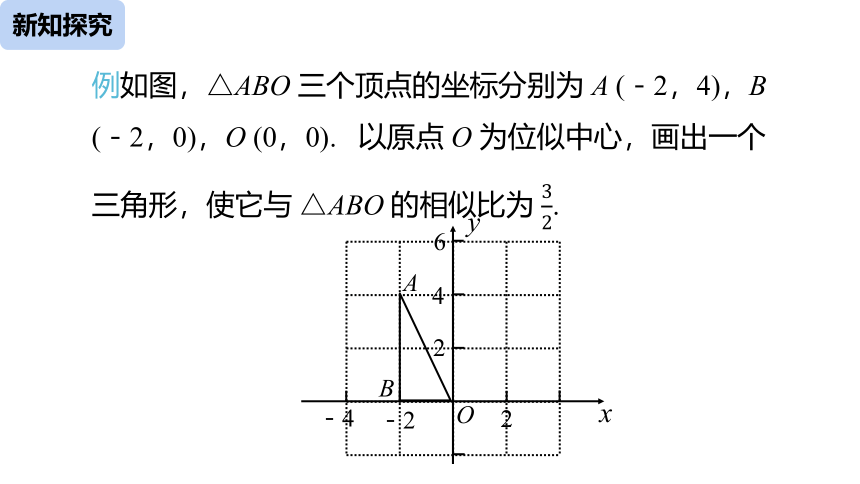
例如图,△ABO 三个顶点的坐标分别为 A (-2,4),B (-2,0),O (0,0). 以原点 O 为位似中心,画出一个三角形,使它与 △ABO 的相似比为 32.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
6
2
-2
-4
x
y
A
B
O
新知探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
6
2
-2
-4
x
y
A
B
O
解:如图,利用位似中对应点的坐标的变化规律,分别取点 A′ (-3,6),B′ (-3,0),O (0,0). 顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.
A′
B′
还有其他画法吗?
新知探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
6
2
-2
-4
x
y
A
B
O
-2
-4
-6
解:利用位似中对应点的坐标的变化规律,分别取点 A′ (3,-6),B′ (3,0),O (0,0). 顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.
A′
B′
新知探究
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在下图所示的图案中,你能找到这些变换吗?
新知探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
规律
变换方式
平移
对应点的横坐标或纵坐标加上(或减去)平移的单位长度
全等变换
轴对称
若以 x 轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;若以 y 轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数
旋转
若一个图形绕原点旋转180°,则旋转前后的两个图形对应点的横坐标与纵坐标都互为相反数
位似
若以原点为位似中心,则变换前后两个图形对应点的横坐标或纵坐标之比的绝对值等于相似比
相似变换(扩大、缩小或不变)
跟踪训练
如图,在平面直角坐标系中,矩形 OABC 的顶点 O 为坐标原点,边 OA 在 x 轴上,OC 在 y 轴上,如果矩形 ????????′????′????′ 与矩形 OABC 关于点 O 位似,且矩形 ????????′????′????′ 的面积等于矩形 OABC 面积的 14 ,那么点 ????′ 的坐标是( )
A.( -2,3)B.(2,-3)
C.(3,-2)或(-2,3)D.(-2,3)或(2,-3)
?
相似比为????????
?
D
随堂练习
1.如图,△ABC 中,A,B 两点在 x 轴的上方,点 C 的坐标是(-1,0).以点 C 为位似中心,在 x 轴的下方作△ABC 的位似图形△????′????′????,并把△ABC 的边长放大到原来的 2 倍.设点 B 的对应点 ????′ 的横坐标是2,则点 B 的橫坐标为.
?
解析:如图,过点 B,B' 分别作 BD⊥x 轴于点 D,B'E⊥x 轴于点 E,
∴ ∠BDC =∠B'EC=90°.
∵△ABC 的位似图形是△A'B'C,
∴ 点 B,C,B' 在一条直线上,
∴∠BCD=∠B'CE,∴△BCD∽△B'CE,
∴ ????????????????=????′????????????=2 ,
?
随堂练习
D
E
随堂练习
∵点 B' 的横坐标是2,点 C 的坐标是(-1,0),
∴CE =3,∴CD =32, ∴????????=52,
∴ 点 B 的横坐标为 ?52 .
?
D
E
随堂练习
2.如图所示,正方形 OEFG 和正方形 ABCD 是位似图形,点 F 的坐标为(-1,1),点 C 的坐标为(-4,2),求这两个正方形位似中心的坐标.
随堂练习
勿忘分类讨论
本题两个正方形位似有两种情况,切记进行分类讨论.
随堂练习
解:(1)当两个正方形位于位似中心同侧时,作直线 CF(图略),位似中心就是直线 CF 与 x 轴的交点,
设直线 CF 的解析式为 y=kx+b.
将点 C(-4,2),F(-1,1)代入,得 ?4????+????=2,?????+????=1,
解得????=?13,????=23,即 ????=?13????+23.令 y =0,得 x =2.
所以这两个正方形位似中心的坐标是(2,0).
?
随堂练习
解:(2)当两个正方形位于位似中心两侧时,作直线 OC,DE(图略),位似中心就是直线 OC与直线 DE的交点.
由题意,得直线 OC的解析式为 ????=?12???? ,直线 DE的解析式为 ????=14????+1 .
由 ????=?12????,????=14????+1,解得????=?43,????=23,
即位似中心的坐标是( ?43 ,23?).
?
随堂练习
找位似中心的方法
位似图形中对应顶点所在的直线相交于位似中心.利用这一性质,只要用直尺把位似图形中的对应顶点所在直线的交点找出来,即可找到位似中心.在此类题中,要注意相关线段的长度与点的坐标之间的相互转化.
随堂练习
3.工人师傅要在三角形铝板上截下一个正方形 DEFG,使 D,E 两点分别在三角形的边 AB,AC 上,F,G 两点在边 BC 上,你能帮他画出裁剪线吗?
解:(1)作正方形 D1E1F1G1,使 D1在边 AB 上,F1,G1在边 BC 上;
(2)作射线 BE1,交 AC 于点 E;
(3)作 DE//BC,交 AB 于点 D,作 EF⊥BC 于
点 F,作DG⊥BC 于点 G,则四边形 DEFG
就是所求的正方形.
A
B
C
D1
G1
F1
E1
E
D
G
F
课堂小结
平面直角坐标系中的位似
平面直角坐标系中的位似变换
坐标变化规律
平面直角坐标系中的位似图形的画法
平面直角坐标系中图形的变换
平移
轴对称
旋转
位似
对接中考
1.(2019·烟台中考)如图,在直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO 的顶点坐标分别为 A( -2,-1),B( -2,-3),O(0,0),△A1B1O1 的顶点坐标分别为 A1(1,-1),B1(1,-5),O1(5,1),△ABO 与
△A1B1O1 是以点 P 为位似中心
的位似图形,则 P 点的坐标为
.
(-5,-1)
P
对接中考
2.(滨州中考)在平面直角坐标系中,△ABO 三个顶点的坐标分别为 A(-2,4),B(-4,0),O(0,0).以原点 O为位似中心,把这个三角形缩小为原来的 12 ,得到△CDO,则点 A 的对应点 C 的坐标是.
?
(-1,2)或(1,-2)
在点 O 同侧时,(?2×12,4×12),即(?1,2).
在点 O 异侧时,(?2×(?12),4×(?12)),即(1,?2).
?
对接中考
3.(2020·重庆中考)如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,则线段DF的长度为( )
A. 5 B. 2
C. 4 D. 25
?
D
D(2,4), F(6,2)
课后作业
请完成课本后习题第3、5题.
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
27.3 位似
相 似
知识回顾
两个相似多边形,如果它们对应顶点所在的直线相交于一点,我们就把这样的两个图形叫做位似图形.
位似图形的概念是什么?
学习目标
1.理解平面直角坐标系中,位似图形对应点的坐标之间的联系.
2.会用图形的坐标的变化表示图形的位似变换,掌握把一个图形按一定比例放大或缩小后,点的坐标变化的规律.
3.了解四种图形变换 (平移、轴对称、旋转和位似) 的异同,并能在复杂图形中找出来这些变换.
课堂导入
我们知道,在直角坐标系中,可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、轴对称和旋转 (中心对称). 那么,位似是否也可以用两个图形坐标之间的关系来表示呢?
新知探究
知识点1:平面直角坐标系中的位似变换
在平面直角坐标系中,有两点 A (6,3),B (6,0).以原点 O 为位似中心,相似比为 ,把线段 AB 缩小.
观察对应点之间坐标有什么变化.
新知探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
6
4
6
B'
-2
-4
-4
x
y
A
B
A'
A"
B"
O
如图,把 AB 缩小后, A,B 的对应点为A′ (2,1),B′ (2,0);A" (-2,-1),B" (-2,0).
新知探究
△ABC 三个顶点坐标分别为 A (2,3),B (2,1),C (5,2),以点 O 为位似中心,相似比为 2,将△ABC 放大.
观察对应顶点坐标有什么变化.
新知探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-6
B'
A'
C'
A"
B"
C"
如图,把 △ABC 放大后 A,B,C 的对应点为A' (4,6),B' (4,2),C' (10,4);A" (-4,-6),B" (-4,-2),C" (-10,-4).
O
新知探究
在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
两个.
新知探究
所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
当位似图形在原点同侧时,其对应顶点的坐标的比为 k;当位似图形在原点两侧时,其对应顶点的坐标的比为 -k.
新知探究
平面直角坐标系中位似变换坐标的变化规律:一般地,在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为 k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
上面的坐标的变化规律是以原点为位似中心的位似变换中图形上对应点的坐标的变化规律.
新知探究
例如图,△ABO 三个顶点的坐标分别为 A (-2,4),B (-2,0),O (0,0). 以原点 O 为位似中心,画出一个三角形,使它与 △ABO 的相似比为 32.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
6
2
-2
-4
x
y
A
B
O
新知探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
6
2
-2
-4
x
y
A
B
O
解:如图,利用位似中对应点的坐标的变化规律,分别取点 A′ (-3,6),B′ (-3,0),O (0,0). 顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.
A′
B′
还有其他画法吗?
新知探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
2
4
6
2
-2
-4
x
y
A
B
O
-2
-4
-6
解:利用位似中对应点的坐标的变化规律,分别取点 A′ (3,-6),B′ (3,0),O (0,0). 顺次连接点 A′ ,B′ ,O,所得的 △A′ B′ O 就是要画的一个图形.
A′
B′
新知探究
至此,我们已经学习了四种变换:平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在下图所示的图案中,你能找到这些变换吗?
新知探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名称
规律
变换方式
平移
对应点的横坐标或纵坐标加上(或减去)平移的单位长度
全等变换
轴对称
若以 x 轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;若以 y 轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数
旋转
若一个图形绕原点旋转180°,则旋转前后的两个图形对应点的横坐标与纵坐标都互为相反数
位似
若以原点为位似中心,则变换前后两个图形对应点的横坐标或纵坐标之比的绝对值等于相似比
相似变换(扩大、缩小或不变)
跟踪训练
如图,在平面直角坐标系中,矩形 OABC 的顶点 O 为坐标原点,边 OA 在 x 轴上,OC 在 y 轴上,如果矩形 ????????′????′????′ 与矩形 OABC 关于点 O 位似,且矩形 ????????′????′????′ 的面积等于矩形 OABC 面积的 14 ,那么点 ????′ 的坐标是( )
A.( -2,3)B.(2,-3)
C.(3,-2)或(-2,3)D.(-2,3)或(2,-3)
?
相似比为????????
?
D
随堂练习
1.如图,△ABC 中,A,B 两点在 x 轴的上方,点 C 的坐标是(-1,0).以点 C 为位似中心,在 x 轴的下方作△ABC 的位似图形△????′????′????,并把△ABC 的边长放大到原来的 2 倍.设点 B 的对应点 ????′ 的横坐标是2,则点 B 的橫坐标为.
?
解析:如图,过点 B,B' 分别作 BD⊥x 轴于点 D,B'E⊥x 轴于点 E,
∴ ∠BDC =∠B'EC=90°.
∵△ABC 的位似图形是△A'B'C,
∴ 点 B,C,B' 在一条直线上,
∴∠BCD=∠B'CE,∴△BCD∽△B'CE,
∴ ????????????????=????′????????????=2 ,
?
随堂练习
D
E
随堂练习
∵点 B' 的横坐标是2,点 C 的坐标是(-1,0),
∴CE =3,∴CD =32, ∴????????=52,
∴ 点 B 的横坐标为 ?52 .
?
D
E
随堂练习
2.如图所示,正方形 OEFG 和正方形 ABCD 是位似图形,点 F 的坐标为(-1,1),点 C 的坐标为(-4,2),求这两个正方形位似中心的坐标.
随堂练习
勿忘分类讨论
本题两个正方形位似有两种情况,切记进行分类讨论.
随堂练习
解:(1)当两个正方形位于位似中心同侧时,作直线 CF(图略),位似中心就是直线 CF 与 x 轴的交点,
设直线 CF 的解析式为 y=kx+b.
将点 C(-4,2),F(-1,1)代入,得 ?4????+????=2,?????+????=1,
解得????=?13,????=23,即 ????=?13????+23.令 y =0,得 x =2.
所以这两个正方形位似中心的坐标是(2,0).
?
随堂练习
解:(2)当两个正方形位于位似中心两侧时,作直线 OC,DE(图略),位似中心就是直线 OC与直线 DE的交点.
由题意,得直线 OC的解析式为 ????=?12???? ,直线 DE的解析式为 ????=14????+1 .
由 ????=?12????,????=14????+1,解得????=?43,????=23,
即位似中心的坐标是( ?43 ,23?).
?
随堂练习
找位似中心的方法
位似图形中对应顶点所在的直线相交于位似中心.利用这一性质,只要用直尺把位似图形中的对应顶点所在直线的交点找出来,即可找到位似中心.在此类题中,要注意相关线段的长度与点的坐标之间的相互转化.
随堂练习
3.工人师傅要在三角形铝板上截下一个正方形 DEFG,使 D,E 两点分别在三角形的边 AB,AC 上,F,G 两点在边 BC 上,你能帮他画出裁剪线吗?
解:(1)作正方形 D1E1F1G1,使 D1在边 AB 上,F1,G1在边 BC 上;
(2)作射线 BE1,交 AC 于点 E;
(3)作 DE//BC,交 AB 于点 D,作 EF⊥BC 于
点 F,作DG⊥BC 于点 G,则四边形 DEFG
就是所求的正方形.
A
B
C
D1
G1
F1
E1
E
D
G
F
课堂小结
平面直角坐标系中的位似
平面直角坐标系中的位似变换
坐标变化规律
平面直角坐标系中的位似图形的画法
平面直角坐标系中图形的变换
平移
轴对称
旋转
位似
对接中考
1.(2019·烟台中考)如图,在直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO 的顶点坐标分别为 A( -2,-1),B( -2,-3),O(0,0),△A1B1O1 的顶点坐标分别为 A1(1,-1),B1(1,-5),O1(5,1),△ABO 与
△A1B1O1 是以点 P 为位似中心
的位似图形,则 P 点的坐标为
.
(-5,-1)
P
对接中考
2.(滨州中考)在平面直角坐标系中,△ABO 三个顶点的坐标分别为 A(-2,4),B(-4,0),O(0,0).以原点 O为位似中心,把这个三角形缩小为原来的 12 ,得到△CDO,则点 A 的对应点 C 的坐标是.
?
(-1,2)或(1,-2)
在点 O 同侧时,(?2×12,4×12),即(?1,2).
在点 O 异侧时,(?2×(?12),4×(?12)),即(1,?2).
?
对接中考
3.(2020·重庆中考)如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,则线段DF的长度为( )
A. 5 B. 2
C. 4 D. 25
?
D
D(2,4), F(6,2)
课后作业
请完成课本后习题第3、5题.
