人教版数学九年级下册27.3 位似 课时1课件(41张)
文档属性
| 名称 | 人教版数学九年级下册27.3 位似 课时1课件(41张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 22:07:33 | ||
图片预览




文档简介
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
27.3 位似
相 似
知识回顾
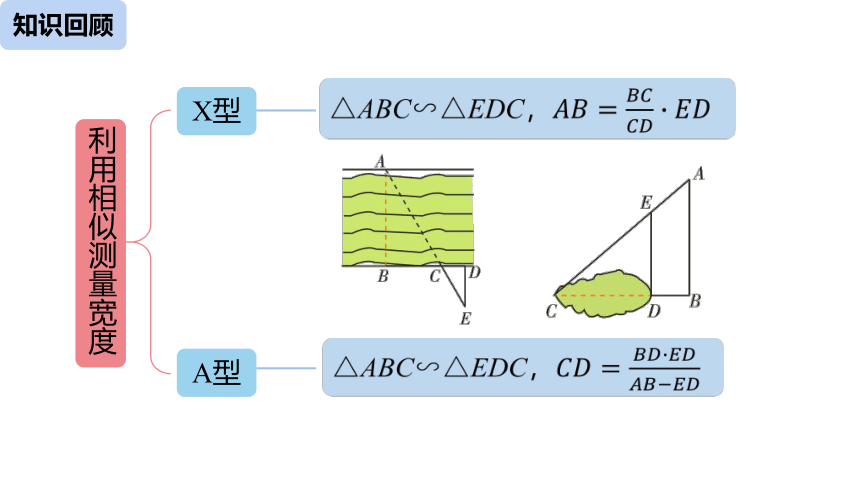
利用相似测量宽度
X型
A型
△ABC∽△EDC,????????=??????????????????????????????????
?
△ABC∽△EDC,????????=?????????????????????????
?
学习目标
1.掌握位似图形的概念、性质和画法.
2.掌握位似与相似的联系与区别.
课堂导入
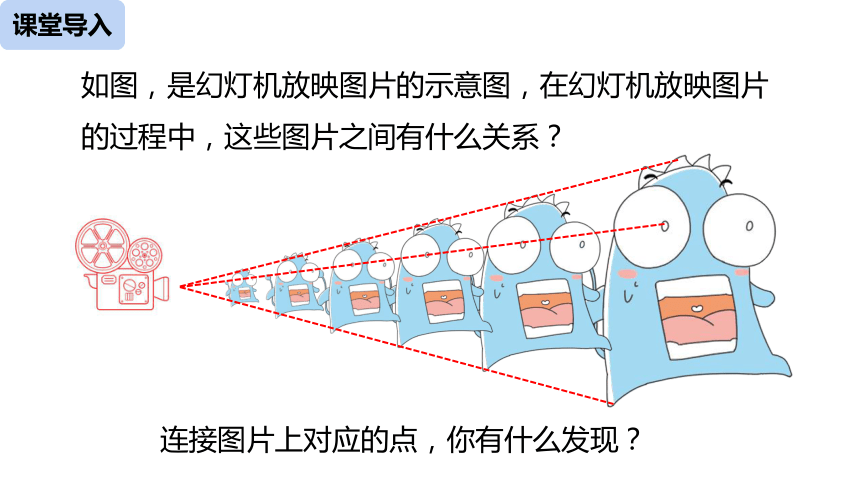
如图,是幻灯机放映图片的示意图,在幻灯机放映图片的过程中,这些图片之间有什么关系?
连接图片上对应的点,你有什么发现?
新知探究
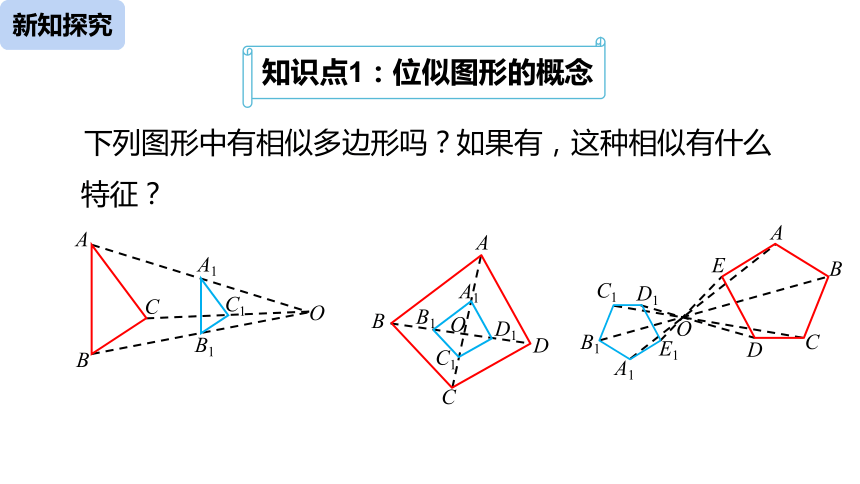
知识点1:位似图形的概念
下列图形中有相似多边形吗?如果有,这种相似有什么特征?
A
B
C
A1
B1
C1
O
O
O
A
B
C
D
A1
B1
C1
D1
A1
B1
C1
D1
E1
A
B
C
D
E
新知探究
两个相似多边形,如果它们对应顶点的连线相交于一点,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心.这时我们说这两个图形关于这点位似.
位似图形必须同时满足两个条件:
1.两个图形是相似图形;
2.两个相似图形的对应顶点的连线相交于同一点.
新知探究
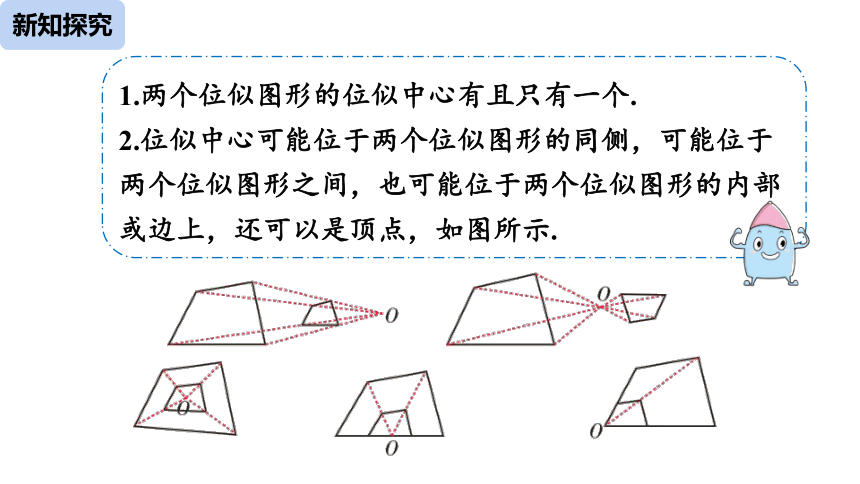
1.两个位似图形的位似中心有且只有一个.
2.位似中心可能位于两个位似图形的同侧,可能位于两个位似图形之间,也可能位于两个位似图形的内部或边上,还可以是顶点,如图所示.
新知探究
1.相似只要求两个图形的形状完全相同,而位似不仅要求图形相似,还必须有特殊的位置关系,即对应顶点的连线相交于同一点.
2.如果两个图形是位似图形,那么这两个图形必是相似图形,但相似的两个图形不一定是位似图形.
位似与相似的区别与联系
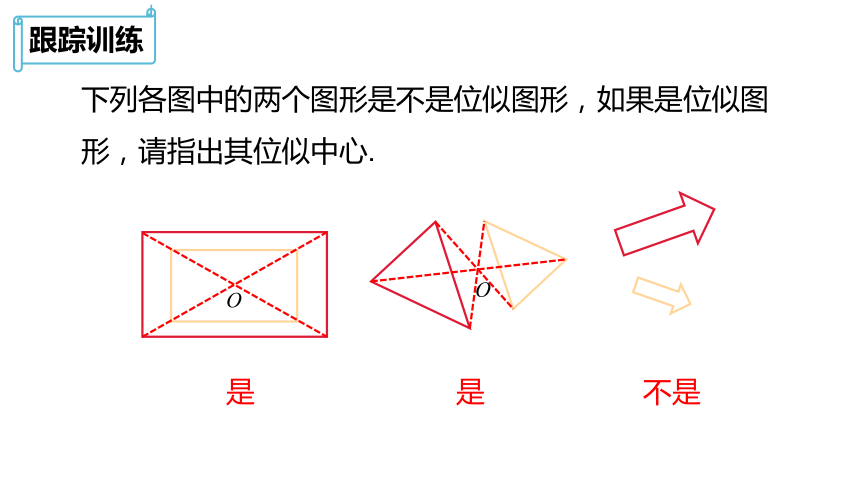
跟踪训练
下列各图中的两个图形是不是位似图形,如果是位似图形,请指出其位似中心.
O
O
是
不是
是
新知探究
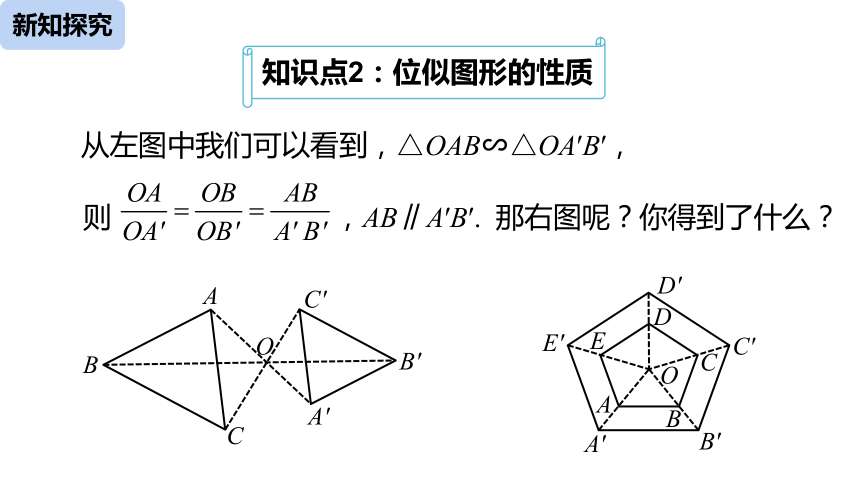
知识点2:位似图形的性质
从左图中我们可以看到,△OAB∽△OA′B′,
则 ,AB∥A′B′. 那右图呢?你得到了什么?
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
新知探究
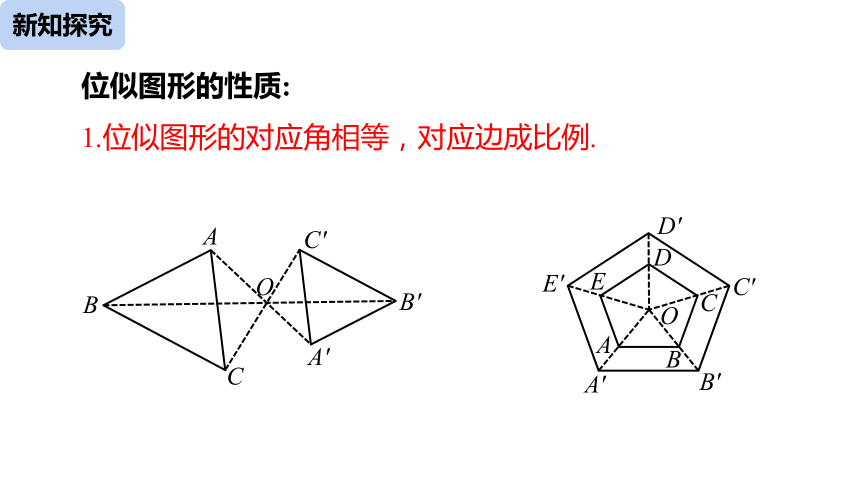
位似图形的性质:
1.位似图形的对应角相等,对应边成比例.
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
新知探究
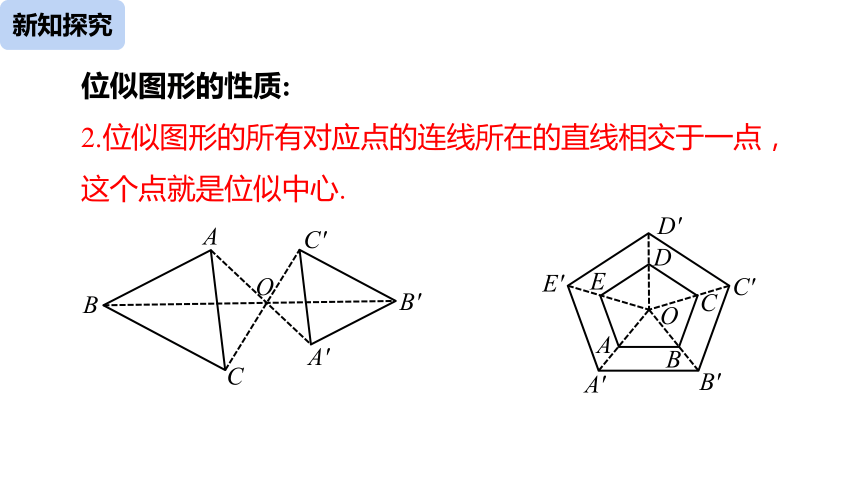
位似图形的性质:
2.位似图形的所有对应点的连线所在的直线相交于一点,这个点就是位似中心.
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
新知探究
位似图形的性质:
3.位似图形的对应边互相平行或在同一条直线上.
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
新知探究
位似图形的性质:
4.位似图形上任意一对对应点,到位似中心的距离之比等于相似比.(仅适用于对应点到位似中心的距离不等于0的情况)
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
新知探究
位似图形的性质:
5.两个图形位似,则这两个图形一定相似,其相似比等于对应边的比,周长比等于相似比,面积比等于相似比的平方.
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
如图,△ABC 与△????′????′????′ 是位似图形,点 O是位似中心,若 ????????=2????????′,则△ABC 与△????′????′????′的相似比为.
?
性质4:位似图形上任意一对对应点,到位似中心的距离之比等于相似比.
2
跟踪训练
新知探究
知识点3:画位似图形
O
D
A
B
C
解:(1) 在四边形外任选一点 O ,连接 OA,OB,OC,OD;
例 把四边形 ABCD 缩小到原来的 .
新知探究
O
D
A
B
C
A'
B'
C'
D'
(2) 分别在线段 OA、OB、OC、OD 上取点 A' 、B' 、C' 、D' ,使得 ;
新知探究
(3) 顺次连接点 A' 、B' 、C' 、D' ,所得四边形 A' B' C' D' 就是所要求的图形.
O
D
A
B
C
A'
B'
C'
D'
利用位似,可以将一个图形放大或缩小.
新知探究
对于上面的问题,你还有其他方法吗?如果在四边形外任选一个点 O,分别在 OA、OB、OC、OD 的反向延长线上取 A′ 、B′ 、C′、D′,使得 呢?
O
D
A
B
C
A'
B'
C'
D'
新知探究
如果点 O 取在四边形 ABCD 内部呢?分别画出这时得到的四边形A' B' C' D' .
O
D
A
B
C
A'
B'
C'
D'
新知探究
画位似图形的一般步骤:
确定位似中心(位似中心可以在两个图形的同侧,或两个图形之间,或图形内,或边上,也可以是顶点),并找出原图形的关键点;
分别连接位似中心和原图形的关键点;
根据相似比,在位似中心与各关键点所确定的直线上取点,确定所画位似图形的关键点的位置;
顺次连接所作各点,得到放大或缩小的图形.
1
2
3
4
新知探究
1.画位似图形时,要弄清相似比,即分清是原图形与新图形的相似比,还是新图形与原图形的相似比.
2.以一点为位似中心画位似图形时,符合要求的图形往往不唯一,一般情况下,同一个位似中心的两侧各有一个符合要求的图形.
跟踪训练
如图,以点 O为位似中心,在点 O的同侧将△ABC 缩小为原来的 12.
?
A
B
C
O
B1
A1
C1
1.下列图形中△ABC ∽△DEF,但这两个三角形不是位似图形的是( )
随堂练习
B
注意对应顶点
随堂练习
判断相似图形是不是位似图形时,需过所有对应点作直线,观察所作直线是否交于一点,若交于一点,则是;否则不是.解本题时切记先判断对应点,再作直线,否则易误认为选项B中的图形也是位似图形.
随堂练习
2.如图,以点 O 为位似中心,将五边形 ABCDE 放大后得到五边形????′????′????′????′????′,已知 OA =10 cm,????????′=20 cm,则五边形 ABCDE 的周长与五边形 ????′????′????′????′????′?的周长的比值是.
?
随堂练习
解析:因为五边形 ABCDE 与五边形 ????′????′????′????′????′ 位似,位似中心为 O, OA =10 cm,????????′=20 cm,所以五边形 ABCDE 与五边形 ????′????′????′????′????′ 的相似比为 ????????????′????′=????????????????′=12 ,所以五边形 ABCDE 与五边形 ????′????′????′????′????′ 的周长比为 12 .
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
随堂练习
3.如图,图中的小方格都是边长为 1 的正方形,△ABC 与△????′????′????′ 的顶点都在格点上. △????′????′????′ 与△ABC 是位似图形吗?如果是,在图形上画出位似中心并求出相似比;如果不是,请说明理由.
?
C
A
B
????′
?
????′
?
????′
?
随堂练习
解:由勾股定理,得 AB= 32+22 = 13 ,BC= 22+12 = 5 ,AC= 22+42 = 25 ; ????′????′=62+42=213,????′????′=42+22=25?,????′????′=42+82=45?.
因为 ????′????′????????=2,????′????′????????=2 ,????′????′????????=2 ,
所以 ????′????′????????=????′????′????????=????′????′???????? ,
所以 △????′????′????′∽△ABC.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
C
A
B
????′
?
????′
?
????′
?
随堂练习
如图,连接 ????′????,????′????,????′???? 并延长相交于一点O,
因此△????′????′????′与△ABC 是位似图形,点 O 即为位似中心,
因为 ????????′=12,OA=6,所以相似比为????????′????????=126=2.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
C
A
B
????′
?
????′
?
????′
?
O
随堂练习
在判定 △????′????′????′ 与△ABC是不是位似图形时,容易出现只考虑两个三角形的对应顶点的连线相交于同一点,而没有证明两个三角形相似的情况.如下图所示,虽然△A2B2C2 与△A1B1C1 对应顶点的连线交于一点,但
是两个三角形不是相似三角形,显然不
是位似图形.
?
两个相似多边形,如果它们对应顶点的连线相交于一点,我们就把这样的两个图形叫做位似图形
课堂小结
位似图形
概念
性质
对应角相等,对应边成比例
对应点的连线所在的直线相交于一点
对应边互相平行或在同一条直线上
位似图形上任意一对对应点,到位似中心的距离之比等于相似比
两个图形位似,则这两个图形一定相似
课堂小结
位似图形的画法
确定位似中心,并找出原图形的关键点
分别连接位似中心和原图形的关键点
确定所画位似图形的关键点的位置
顺次连接所作各点,得到放大或缩小的图形
对接中考
1.(2019·邵阳中考)如图,以点 O为位似中心,把△ABC 放大为原图形的2倍得到△????′????′????′,以下说法中错误的是( )
A.△ABC∽△????′????′????′
B.点C、点O、点C'三点在同一直线上
C.AO:AA' =1:2
D.AB∥ A'B'
?
C
1:3
对接中考
2.(2020·河北中考)在如图所示的网格中,以点 O 为位似中心,四边形 ABCD 的位似图形是( )
A.四边形 NPMQ
B.四边形 NPMR
C.四边形 NHMQ
D.四边形 NHMR
解析:∵以点O 为位似中心,∴点C对应点M,
设网格中每个小方格的边长为1,
则OC=5,OM=25?,OD=2?,
OB=10?,OA=13?,OR=5?,
OQ=22?,OP=210?,OH=35?,
ON=213?,
∵????????????????=????????????????=????????????????=????????????????=12,
∴以点O为位似中心,四边形ABCD的位似图形是
四边形NPMQ.
?
对接中考
对接中考
3.(2018·凉山州中考)如图,△ABC 在方格纸中.
(1)请在方格纸上建立平面直
角坐标系,使 A(2,3),
C(6,2),并求出 B 点坐标;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
A
B
C
O
x
y
B点坐标 (2,1)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
A
B
C
O
x
y
对接中考
(2)以原点 O为位似中心,相似比为2,在第一象限内将△ABC 放大,画出放大后的图形△????′????′????′;
?
????′
?
????′
?
????′
?
对接中考
(3)计算△????′????′????′ 的面积 S.
?
解:S=12×4×8=16.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
????′
?
????′
?
????′
?
A
B
C
O
x
y
课后作业
请完成课本后习题第2、4题.
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
27.3 位似
相 似
知识回顾
利用相似测量宽度
X型
A型
△ABC∽△EDC,????????=??????????????????????????????????
?
△ABC∽△EDC,????????=?????????????????????????
?
学习目标
1.掌握位似图形的概念、性质和画法.
2.掌握位似与相似的联系与区别.
课堂导入
如图,是幻灯机放映图片的示意图,在幻灯机放映图片的过程中,这些图片之间有什么关系?
连接图片上对应的点,你有什么发现?
新知探究
知识点1:位似图形的概念
下列图形中有相似多边形吗?如果有,这种相似有什么特征?
A
B
C
A1
B1
C1
O
O
O
A
B
C
D
A1
B1
C1
D1
A1
B1
C1
D1
E1
A
B
C
D
E
新知探究
两个相似多边形,如果它们对应顶点的连线相交于一点,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心.这时我们说这两个图形关于这点位似.
位似图形必须同时满足两个条件:
1.两个图形是相似图形;
2.两个相似图形的对应顶点的连线相交于同一点.
新知探究
1.两个位似图形的位似中心有且只有一个.
2.位似中心可能位于两个位似图形的同侧,可能位于两个位似图形之间,也可能位于两个位似图形的内部或边上,还可以是顶点,如图所示.
新知探究
1.相似只要求两个图形的形状完全相同,而位似不仅要求图形相似,还必须有特殊的位置关系,即对应顶点的连线相交于同一点.
2.如果两个图形是位似图形,那么这两个图形必是相似图形,但相似的两个图形不一定是位似图形.
位似与相似的区别与联系
跟踪训练
下列各图中的两个图形是不是位似图形,如果是位似图形,请指出其位似中心.
O
O
是
不是
是
新知探究
知识点2:位似图形的性质
从左图中我们可以看到,△OAB∽△OA′B′,
则 ,AB∥A′B′. 那右图呢?你得到了什么?
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
新知探究
位似图形的性质:
1.位似图形的对应角相等,对应边成比例.
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
新知探究
位似图形的性质:
2.位似图形的所有对应点的连线所在的直线相交于一点,这个点就是位似中心.
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
新知探究
位似图形的性质:
3.位似图形的对应边互相平行或在同一条直线上.
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
新知探究
位似图形的性质:
4.位似图形上任意一对对应点,到位似中心的距离之比等于相似比.(仅适用于对应点到位似中心的距离不等于0的情况)
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
新知探究
位似图形的性质:
5.两个图形位似,则这两个图形一定相似,其相似比等于对应边的比,周长比等于相似比,面积比等于相似比的平方.
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
如图,△ABC 与△????′????′????′ 是位似图形,点 O是位似中心,若 ????????=2????????′,则△ABC 与△????′????′????′的相似比为.
?
性质4:位似图形上任意一对对应点,到位似中心的距离之比等于相似比.
2
跟踪训练
新知探究
知识点3:画位似图形
O
D
A
B
C
解:(1) 在四边形外任选一点 O ,连接 OA,OB,OC,OD;
例 把四边形 ABCD 缩小到原来的 .
新知探究
O
D
A
B
C
A'
B'
C'
D'
(2) 分别在线段 OA、OB、OC、OD 上取点 A' 、B' 、C' 、D' ,使得 ;
新知探究
(3) 顺次连接点 A' 、B' 、C' 、D' ,所得四边形 A' B' C' D' 就是所要求的图形.
O
D
A
B
C
A'
B'
C'
D'
利用位似,可以将一个图形放大或缩小.
新知探究
对于上面的问题,你还有其他方法吗?如果在四边形外任选一个点 O,分别在 OA、OB、OC、OD 的反向延长线上取 A′ 、B′ 、C′、D′,使得 呢?
O
D
A
B
C
A'
B'
C'
D'
新知探究
如果点 O 取在四边形 ABCD 内部呢?分别画出这时得到的四边形A' B' C' D' .
O
D
A
B
C
A'
B'
C'
D'
新知探究
画位似图形的一般步骤:
确定位似中心(位似中心可以在两个图形的同侧,或两个图形之间,或图形内,或边上,也可以是顶点),并找出原图形的关键点;
分别连接位似中心和原图形的关键点;
根据相似比,在位似中心与各关键点所确定的直线上取点,确定所画位似图形的关键点的位置;
顺次连接所作各点,得到放大或缩小的图形.
1
2
3
4
新知探究
1.画位似图形时,要弄清相似比,即分清是原图形与新图形的相似比,还是新图形与原图形的相似比.
2.以一点为位似中心画位似图形时,符合要求的图形往往不唯一,一般情况下,同一个位似中心的两侧各有一个符合要求的图形.
跟踪训练
如图,以点 O为位似中心,在点 O的同侧将△ABC 缩小为原来的 12.
?
A
B
C
O
B1
A1
C1
1.下列图形中△ABC ∽△DEF,但这两个三角形不是位似图形的是( )
随堂练习
B
注意对应顶点
随堂练习
判断相似图形是不是位似图形时,需过所有对应点作直线,观察所作直线是否交于一点,若交于一点,则是;否则不是.解本题时切记先判断对应点,再作直线,否则易误认为选项B中的图形也是位似图形.
随堂练习
2.如图,以点 O 为位似中心,将五边形 ABCDE 放大后得到五边形????′????′????′????′????′,已知 OA =10 cm,????????′=20 cm,则五边形 ABCDE 的周长与五边形 ????′????′????′????′????′?的周长的比值是.
?
随堂练习
解析:因为五边形 ABCDE 与五边形 ????′????′????′????′????′ 位似,位似中心为 O, OA =10 cm,????????′=20 cm,所以五边形 ABCDE 与五边形 ????′????′????′????′????′ 的相似比为 ????????????′????′=????????????????′=12 ,所以五边形 ABCDE 与五边形 ????′????′????′????′????′ 的周长比为 12 .
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
随堂练习
3.如图,图中的小方格都是边长为 1 的正方形,△ABC 与△????′????′????′ 的顶点都在格点上. △????′????′????′ 与△ABC 是位似图形吗?如果是,在图形上画出位似中心并求出相似比;如果不是,请说明理由.
?
C
A
B
????′
?
????′
?
????′
?
随堂练习
解:由勾股定理,得 AB= 32+22 = 13 ,BC= 22+12 = 5 ,AC= 22+42 = 25 ; ????′????′=62+42=213,????′????′=42+22=25?,????′????′=42+82=45?.
因为 ????′????′????????=2,????′????′????????=2 ,????′????′????????=2 ,
所以 ????′????′????????=????′????′????????=????′????′???????? ,
所以 △????′????′????′∽△ABC.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
C
A
B
????′
?
????′
?
????′
?
随堂练习
如图,连接 ????′????,????′????,????′???? 并延长相交于一点O,
因此△????′????′????′与△ABC 是位似图形,点 O 即为位似中心,
因为 ????????′=12,OA=6,所以相似比为????????′????????=126=2.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
C
A
B
????′
?
????′
?
????′
?
O
随堂练习
在判定 △????′????′????′ 与△ABC是不是位似图形时,容易出现只考虑两个三角形的对应顶点的连线相交于同一点,而没有证明两个三角形相似的情况.如下图所示,虽然△A2B2C2 与△A1B1C1 对应顶点的连线交于一点,但
是两个三角形不是相似三角形,显然不
是位似图形.
?
两个相似多边形,如果它们对应顶点的连线相交于一点,我们就把这样的两个图形叫做位似图形
课堂小结
位似图形
概念
性质
对应角相等,对应边成比例
对应点的连线所在的直线相交于一点
对应边互相平行或在同一条直线上
位似图形上任意一对对应点,到位似中心的距离之比等于相似比
两个图形位似,则这两个图形一定相似
课堂小结
位似图形的画法
确定位似中心,并找出原图形的关键点
分别连接位似中心和原图形的关键点
确定所画位似图形的关键点的位置
顺次连接所作各点,得到放大或缩小的图形
对接中考
1.(2019·邵阳中考)如图,以点 O为位似中心,把△ABC 放大为原图形的2倍得到△????′????′????′,以下说法中错误的是( )
A.△ABC∽△????′????′????′
B.点C、点O、点C'三点在同一直线上
C.AO:AA' =1:2
D.AB∥ A'B'
?
C
1:3
对接中考
2.(2020·河北中考)在如图所示的网格中,以点 O 为位似中心,四边形 ABCD 的位似图形是( )
A.四边形 NPMQ
B.四边形 NPMR
C.四边形 NHMQ
D.四边形 NHMR
解析:∵以点O 为位似中心,∴点C对应点M,
设网格中每个小方格的边长为1,
则OC=5,OM=25?,OD=2?,
OB=10?,OA=13?,OR=5?,
OQ=22?,OP=210?,OH=35?,
ON=213?,
∵????????????????=????????????????=????????????????=????????????????=12,
∴以点O为位似中心,四边形ABCD的位似图形是
四边形NPMQ.
?
对接中考
对接中考
3.(2018·凉山州中考)如图,△ABC 在方格纸中.
(1)请在方格纸上建立平面直
角坐标系,使 A(2,3),
C(6,2),并求出 B 点坐标;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
A
B
C
O
x
y
B点坐标 (2,1)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
A
B
C
O
x
y
对接中考
(2)以原点 O为位似中心,相似比为2,在第一象限内将△ABC 放大,画出放大后的图形△????′????′????′;
?
????′
?
????′
?
????′
?
对接中考
(3)计算△????′????′????′ 的面积 S.
?
解:S=12×4×8=16.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
????′
?
????′
?
????′
?
A
B
C
O
x
y
课后作业
请完成课本后习题第2、4题.
