苏科版九年级数学上册随堂练——2.2圆的对称性提升练习(Word版含答案)
文档属性
| 名称 | 苏科版九年级数学上册随堂练——2.2圆的对称性提升练习(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 165.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 15:25:51 | ||
图片预览

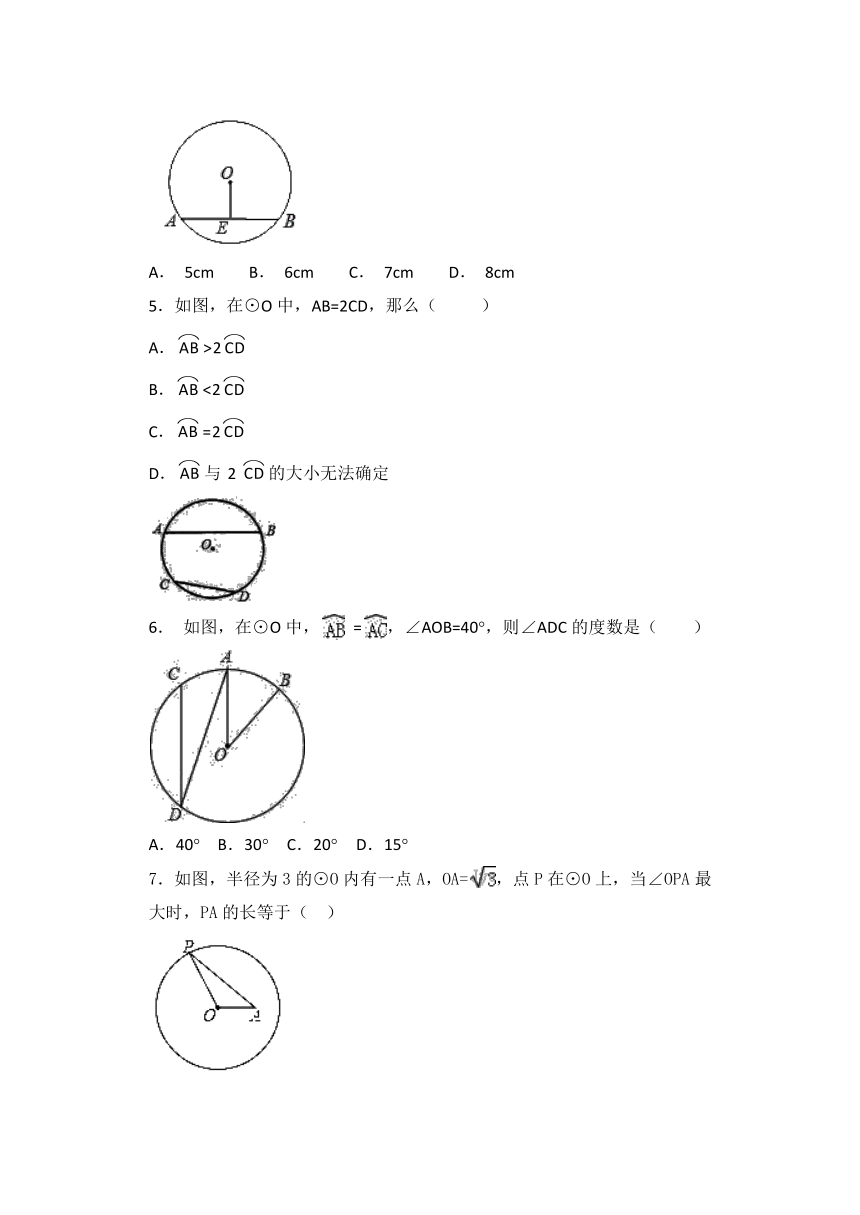

文档简介
2.2圆的对称性提升练习
一、选择题
1.如图,AB.CD是⊙O的直径,AB∥DE.则(
)
A.
AC=AE
B.
AC>AE
C.
AC<AE
D.
AC与AE的大小无法确定
2.
如图,BD是⊙O的直径,点A、C在⊙O上,
=,∠AOB=60°,则∠BDC的度数是( )
A.60°
B.45°
C.35°
D.30°
3.如图,AB,CD是⊙O的直径,AB∥ED,则(
)
A.AC=AE
B.AC>AE
C.AC<AE
D.AC与AE的大小关系无法确定
4.如图,已知⊙O的半径为10cm,弦AB的长为12cm,则弦AB的弦心距OE的长为(
)
A.
5cm
B.
6cm
C.
7cm
D.
8cm
5.如图,在⊙O中,AB=2CD,那么(
)
A.>2
B.<2
C.=2
D.与2的大小无法确定
6.
如图,在⊙O中,
=,∠AOB=40°,则∠ADC的度数是( )
A.40°
B.30°
C.20°
D.15°
7.如图,半径为3的⊙O内有一点A,OA=,点P在⊙O上,当∠OPA最大时,PA的长等于(
)
A.
B.
C.3
D.2
8.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意,CD长为(
)
A.12寸
B.13寸
C.24寸
D.26寸
9.如图,已知⊙O的直径AB=12,E、F为AB的三等分点,M、N为弧AB上两点,且∠MEB=∠NFB=60°,则EM+FN=(
)
A、
B、
C、
D、33
10.如图,∠AOB=90°,C,D是三等分点,AB分别交OC,OD于点E,F,则下列正确的有(
)
①AE+BF=2CD;
②AE=BF=CD;
③
AE·BF=CD2
④AE=BF>CD.
A.1个
B.2个
C.3个
D.4个
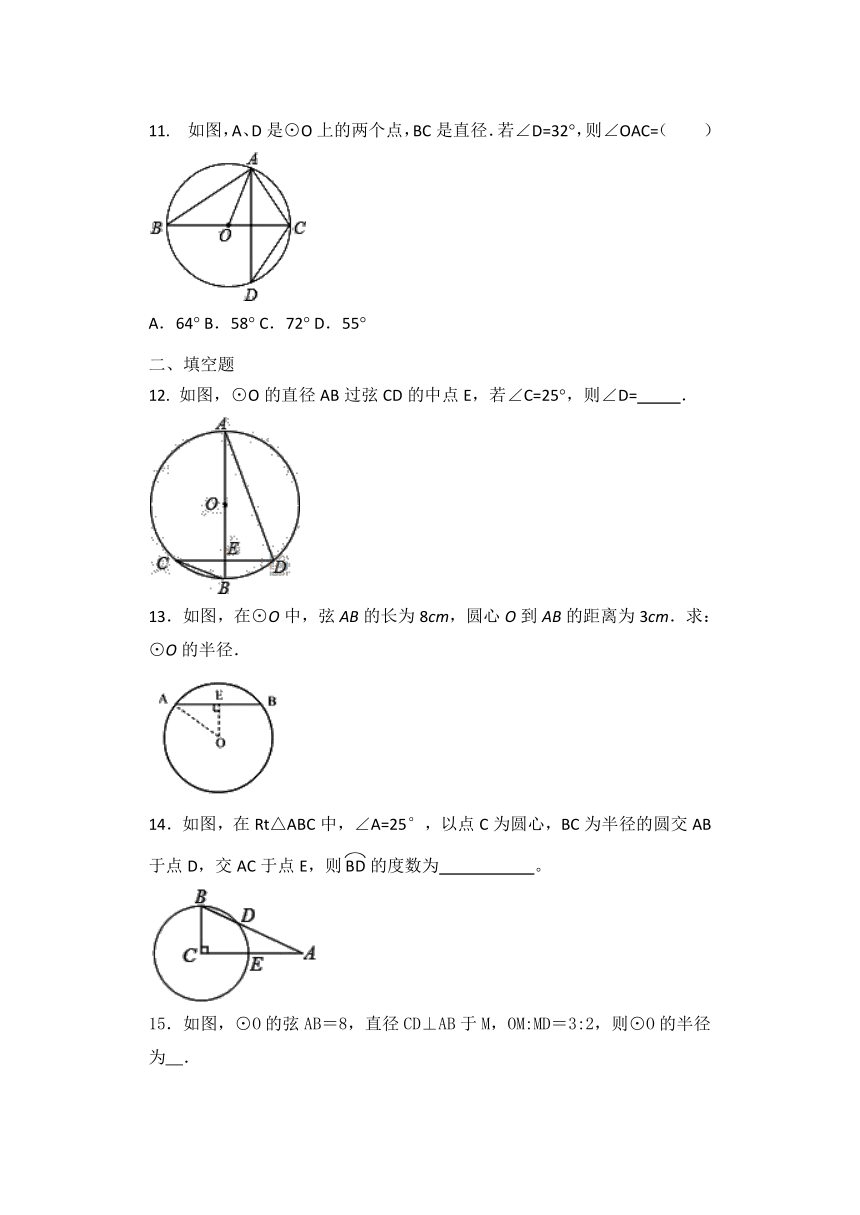
11.
如图,A、D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=( )
A.64°
B.58°
C.72°
D.55°
二、填空题
12.
如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=
.
13.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm.求:⊙O的半径.
14.如图,在Rt△ABC中,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为
。
15.如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,则⊙O的半径为
.
16.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为
。
17.⊙的半径为5,弦的长为8,
是弦上的动点,则线段长的最小值为______.
18.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,∠BCD的度数为
。
三、解答题
19.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF
(2)若CD=6,CA=8,求AE的长
20.如图,过⊙O内一点P,作⊙O的弦AB,使它以点P为中点。
21.如图,⊙C经过原点且与两坐标轴分别交于A、B两点,点A的坐标为(0,4),M是圆上一点,∠BMO=120°,求⊙C的半径和圆心C的坐标.
22.如图,A是半圆上的一个三等分点,B是的中点,P是直径MN上一动点,⊙O的半径为1,试确定AP+BP的最小值.
答案
1.
A
2.
D
3.
A
4.
D
5.
A
6.
C
7.
B
8.
D
9.
C
10.
C
11.
B
12.
65°.
13.
5
cm
14.
50°
15.
5
16.
17.
3
18.
120°
19.
(1)
AB是⊙O的直径,
,
,
,
,
C是的中点
,,
,
,
,
(2)
C是的中点
BC=CD=6
在Rt△ABC中,由勾股定理得,
,
,
在Rt△ACE中
,AE=
20.
略
21.
(1)连结AB,易证AB为⊙C的直径。∵∠BMO=120°,
∴∠BAO=60°。∴AB=2AO=8。∴⊙C的半径为R==4。
(2)圆心C的坐标为(-2,2)。
22.
一、选择题
1.如图,AB.CD是⊙O的直径,AB∥DE.则(
)
A.
AC=AE
B.
AC>AE
C.
AC<AE
D.
AC与AE的大小无法确定
2.
如图,BD是⊙O的直径,点A、C在⊙O上,
=,∠AOB=60°,则∠BDC的度数是( )
A.60°
B.45°
C.35°
D.30°
3.如图,AB,CD是⊙O的直径,AB∥ED,则(
)
A.AC=AE
B.AC>AE
C.AC<AE
D.AC与AE的大小关系无法确定
4.如图,已知⊙O的半径为10cm,弦AB的长为12cm,则弦AB的弦心距OE的长为(
)
A.
5cm
B.
6cm
C.
7cm
D.
8cm
5.如图,在⊙O中,AB=2CD,那么(
)
A.>2
B.<2
C.=2
D.与2的大小无法确定
6.
如图,在⊙O中,
=,∠AOB=40°,则∠ADC的度数是( )
A.40°
B.30°
C.20°
D.15°
7.如图,半径为3的⊙O内有一点A,OA=,点P在⊙O上,当∠OPA最大时,PA的长等于(
)
A.
B.
C.3
D.2
8.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意,CD长为(
)
A.12寸
B.13寸
C.24寸
D.26寸
9.如图,已知⊙O的直径AB=12,E、F为AB的三等分点,M、N为弧AB上两点,且∠MEB=∠NFB=60°,则EM+FN=(
)
A、
B、
C、
D、33
10.如图,∠AOB=90°,C,D是三等分点,AB分别交OC,OD于点E,F,则下列正确的有(
)
①AE+BF=2CD;
②AE=BF=CD;
③
AE·BF=CD2
④AE=BF>CD.
A.1个
B.2个
C.3个
D.4个
11.
如图,A、D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=( )
A.64°
B.58°
C.72°
D.55°
二、填空题
12.
如图,⊙O的直径AB过弦CD的中点E,若∠C=25°,则∠D=
.
13.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm.求:⊙O的半径.
14.如图,在Rt△ABC中,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则的度数为
。
15.如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,则⊙O的半径为
.
16.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为
。
17.⊙的半径为5,弦的长为8,
是弦上的动点,则线段长的最小值为______.
18.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,∠BCD的度数为
。
三、解答题
19.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF
(2)若CD=6,CA=8,求AE的长
20.如图,过⊙O内一点P,作⊙O的弦AB,使它以点P为中点。
21.如图,⊙C经过原点且与两坐标轴分别交于A、B两点,点A的坐标为(0,4),M是圆上一点,∠BMO=120°,求⊙C的半径和圆心C的坐标.
22.如图,A是半圆上的一个三等分点,B是的中点,P是直径MN上一动点,⊙O的半径为1,试确定AP+BP的最小值.
答案
1.
A
2.
D
3.
A
4.
D
5.
A
6.
C
7.
B
8.
D
9.
C
10.
C
11.
B
12.
65°.
13.
5
cm
14.
50°
15.
5
16.
17.
3
18.
120°
19.
(1)
AB是⊙O的直径,
,
,
,
,
C是的中点
,,
,
,
,
(2)
C是的中点
BC=CD=6
在Rt△ABC中,由勾股定理得,
,
,
在Rt△ACE中
,AE=
20.
略
21.
(1)连结AB,易证AB为⊙C的直径。∵∠BMO=120°,
∴∠BAO=60°。∴AB=2AO=8。∴⊙C的半径为R==4。
(2)圆心C的坐标为(-2,2)。
22.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
