北师大版七年级数学上册第三章整式及其加减同步测试(附答案)
文档属性
| 名称 | 北师大版七年级数学上册第三章整式及其加减同步测试(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 234.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 11:59:34 | ||
图片预览


文档简介
北师大版七年级数学上册第三章整式及其加减
同步测试2
一.选择题
1.计算-a2+3a2的结果为( )
A.2a2
B.-2a2
C.4a2
D.-4a2
2.多项式1+2xy-3xy2的次数及最高次项的系数分别是(
)
A.3,-3
B.2,-3
C.5,-3
D.2,3
3.下面计算正确的是( )
A.3x2-x2=3
B.3a2+2a3=5a5
C.3+x=3x
D.-0.75ab+ba=0
4.多项式x2-2xy3-y-1是( )
A.三次四项式
B.三次三项式
C.四次四项式
D.四次三项式
5.若-x3ym与xny是同类项,则m+n的值为( )
A.1
B.2
C.3
D.4
6.如图是一个运算程序的示意图,若开始输入x的值为81,则第2
020次输出的结果为(
)
A.3
B.27
C.9
D.1
7.有一条长为l的篱笆,利用它和房屋的一面墙围成如图所示的长方形园子,园子的宽为t,则所围成园子的面积为( )
A.(l-2t)t
B.(l-t)t
C.t
D.t
8.已知单项式2a3bN+1与-3aM-2b2的和仍是单项式,则2M+3N的值为(
)
A.10
B.11
C.12
D.13
9.一家商店以每包a元的价格买进了30包甲种茶叶,又以每包b元的价格买进60包乙种茶叶.如果以每包元的价格卖出这两种茶叶,则卖完后,这家商店( )
A.赚了
B.赔了
C.不赔不赚
D.不能确定赔或赚
10.已知下列一组数:1,,,,,….用代数式表示第N个数,则第N个数是(
)
A.
B.
C.
D.
二.填空题
11.单项式-是
次单项式,系数为
.
12.钢笔每支a元,铅笔每支b元,买2支钢笔和3支铅笔共需 元.
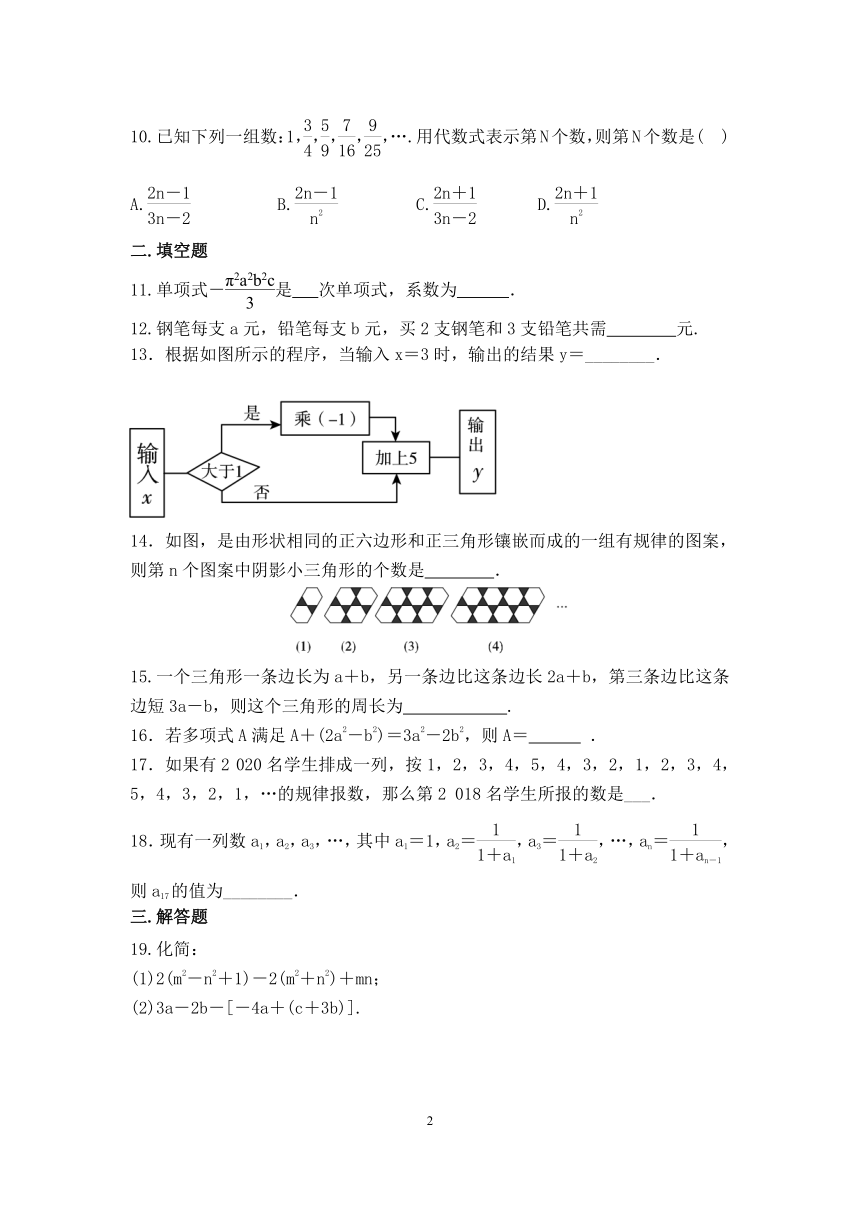
13.根据如图所示的程序,当输入x=3时,输出的结果y=________.
14.如图,是由形状相同的正六边形和正三角形镶嵌而成的一组有规律的图案,则第n个图案中阴影小三角形的个数是
.
15.一个三角形一条边长为a+b,另一条边比这条边长2a+b,第三条边比这条边短3a-b,则这个三角形的周长为 .
16.若多项式A满足A+(2a2-b2)=3a2-2b2,则A=
.
17.如果有2
020名学生排成一列,按1,2,3,4,5,4,3,2,1,2,3,4,5,4,3,2,1,…的规律报数,那么第2
018名学生所报的数是___.
18.现有一列数a1,a2,a3,…,其中a1=1,a2=,a3=,…,an=,则a17的值为________.
三.解答题
19.化简:
(1)2(m2-n2+1)-2(m2+n2)+mn;
(2)3a-2b-[-4a+(c+3b)].
20.先化简,再求值:
(1)-a2b+(3ab2-a2b)-2(2ab2-a2b),其中
a=-1,b=-2.
(2)(6a2-6ab-12b2)-3(2a2-4b2),其中a=-,b=-8.
21.学习了整式的加减运算后,老师给同学们布置了一道课堂练习题“a=-2,b=2
017时,求(3a2b-2ab2+4a)-2(2a2b-3a)+2(ab2+a2b)-1的值”.盈盈做完后对同桌说:“张老师给的条件b=2
017是多余的,这道题不给b的值,照样可以求出结果来.”同桌不相信她的话.亲爱的同学们,你相信盈盈的说法吗?说说你的理由.
22.某商店有一种商品每件成本a元,原来按成本增加b元定价出售,售出40件后,由于库存积压减价,按售价的80%出售,又销售60件.
(1)销售100件这种商品的总售价为多少元?
(2)销售100件这种商品共盈利了多少元?
23.笔记本的单价是x元,圆珠笔的单价是y元.小红买3本笔记本,6支圆珠笔;小明买6本笔记本,3支圆珠笔.
(1)小红和小明买这些笔记本和圆珠笔一共花费多少元钱?
(2)若每本笔记本比每支圆珠笔贵2元,求小明比小红多花费了多少元钱?
24.观察一组数据:2,4,7,11,16,22,29,…,它们有一定的规律,若记第一个数为a1,第二个数记为a2,…,第N个数记为aN.
(1)请写出29后面的第一个数;
(2)通过计算a2-a1,a3-a2,a4-a3,…由此推算a100-a99的值;
(3)根据你发现的规律求a100的值.
25.有理数a,b,c在数轴上的位置如图所示.
(1)c+b 0,a+c 0,b-a 0(填“>”“<”或“=”);
(2)试化简:|b-a|+|a+c|-|c+b|.
答案提示
1.A
2.A
3.D
4.C
5.D6.D 7.A 8.D
9.D
10.B
11.
5
-.
12.(2a+3b)
13.2
14.4n-2或2+4(n-1)
15.2a+5b
16.a2-b2
17.4
18.
解:(1)原式=-4n2+mn+2.
(2)原式=7a-5b-c.
20.(1)解:原式=-a2b+3ab2-a2b-4ab2+2a2b=-ab2.
当a=-1,b=-2时,
原式=-(-1)×(-2)2=4.
(2)
解:原式=6a2-6ab-12b2-6a2+12b2=-6ab.
当a=-,b=-8时,
原式=-6×(-)×(-8)=-24.
21.解:原式=3a2b-2ab2+4a-4a2b+6a+2ab2+a2b-1
=10a-1,
当a=-2时,原式=10×(-2)-1=-21.
因为化简后的结果中不再含有字母b,故最后的结果与b的取值无关,b=2
016这个条件是多余的.
所以盈盈的说法是正确的.
22.
解:(1)根据题意,得40(a+b)+60(a+b)×80%=88a+88b(元),
则销售100件这种商品的总售价为(88a+88b)元.
(2)根据题意,得88a+88b-100a=-12a+88b(元),
则销售100件这种商品共盈利了(-12a+88b)元.
23.解:(1)由题意,得3x+6y+6x+3y=9x+9y,则小红和小明买这些笔记本和圆珠笔一共花费了(9x+9y)元.
(2)由题意,得(6x+3y)-(3x+6y)=3x-3y.
因为每本笔记本比每支圆珠笔贵2元,即x-y=2,所以3x-3y=3(x-y)=6(元),则小明比小红多花费了6元钱.
24.解:(1)29后面的第一个数是37.
(2)由题意,得a2-a1=2,a3-a2=3,a4-a3=4,…,由此推算a100-a99=100.
(3)a100=2+2+3+4+…+100
=1+×100=5
051.
25.解:(1)< < >(3分)
(2)原式=b-a-(a+c)+(c+b)=b-a-a-c+c+b=2b-2a.
同步测试2
一.选择题
1.计算-a2+3a2的结果为( )
A.2a2
B.-2a2
C.4a2
D.-4a2
2.多项式1+2xy-3xy2的次数及最高次项的系数分别是(
)
A.3,-3
B.2,-3
C.5,-3
D.2,3
3.下面计算正确的是( )
A.3x2-x2=3
B.3a2+2a3=5a5
C.3+x=3x
D.-0.75ab+ba=0
4.多项式x2-2xy3-y-1是( )
A.三次四项式
B.三次三项式
C.四次四项式
D.四次三项式
5.若-x3ym与xny是同类项,则m+n的值为( )
A.1
B.2
C.3
D.4
6.如图是一个运算程序的示意图,若开始输入x的值为81,则第2
020次输出的结果为(
)
A.3
B.27
C.9
D.1
7.有一条长为l的篱笆,利用它和房屋的一面墙围成如图所示的长方形园子,园子的宽为t,则所围成园子的面积为( )
A.(l-2t)t
B.(l-t)t
C.t
D.t
8.已知单项式2a3bN+1与-3aM-2b2的和仍是单项式,则2M+3N的值为(
)
A.10
B.11
C.12
D.13
9.一家商店以每包a元的价格买进了30包甲种茶叶,又以每包b元的价格买进60包乙种茶叶.如果以每包元的价格卖出这两种茶叶,则卖完后,这家商店( )
A.赚了
B.赔了
C.不赔不赚
D.不能确定赔或赚
10.已知下列一组数:1,,,,,….用代数式表示第N个数,则第N个数是(
)
A.
B.
C.
D.
二.填空题
11.单项式-是
次单项式,系数为
.
12.钢笔每支a元,铅笔每支b元,买2支钢笔和3支铅笔共需 元.
13.根据如图所示的程序,当输入x=3时,输出的结果y=________.
14.如图,是由形状相同的正六边形和正三角形镶嵌而成的一组有规律的图案,则第n个图案中阴影小三角形的个数是
.
15.一个三角形一条边长为a+b,另一条边比这条边长2a+b,第三条边比这条边短3a-b,则这个三角形的周长为 .
16.若多项式A满足A+(2a2-b2)=3a2-2b2,则A=
.
17.如果有2
020名学生排成一列,按1,2,3,4,5,4,3,2,1,2,3,4,5,4,3,2,1,…的规律报数,那么第2
018名学生所报的数是___.
18.现有一列数a1,a2,a3,…,其中a1=1,a2=,a3=,…,an=,则a17的值为________.
三.解答题
19.化简:
(1)2(m2-n2+1)-2(m2+n2)+mn;
(2)3a-2b-[-4a+(c+3b)].
20.先化简,再求值:
(1)-a2b+(3ab2-a2b)-2(2ab2-a2b),其中
a=-1,b=-2.
(2)(6a2-6ab-12b2)-3(2a2-4b2),其中a=-,b=-8.
21.学习了整式的加减运算后,老师给同学们布置了一道课堂练习题“a=-2,b=2
017时,求(3a2b-2ab2+4a)-2(2a2b-3a)+2(ab2+a2b)-1的值”.盈盈做完后对同桌说:“张老师给的条件b=2
017是多余的,这道题不给b的值,照样可以求出结果来.”同桌不相信她的话.亲爱的同学们,你相信盈盈的说法吗?说说你的理由.
22.某商店有一种商品每件成本a元,原来按成本增加b元定价出售,售出40件后,由于库存积压减价,按售价的80%出售,又销售60件.
(1)销售100件这种商品的总售价为多少元?
(2)销售100件这种商品共盈利了多少元?
23.笔记本的单价是x元,圆珠笔的单价是y元.小红买3本笔记本,6支圆珠笔;小明买6本笔记本,3支圆珠笔.
(1)小红和小明买这些笔记本和圆珠笔一共花费多少元钱?
(2)若每本笔记本比每支圆珠笔贵2元,求小明比小红多花费了多少元钱?
24.观察一组数据:2,4,7,11,16,22,29,…,它们有一定的规律,若记第一个数为a1,第二个数记为a2,…,第N个数记为aN.
(1)请写出29后面的第一个数;
(2)通过计算a2-a1,a3-a2,a4-a3,…由此推算a100-a99的值;
(3)根据你发现的规律求a100的值.
25.有理数a,b,c在数轴上的位置如图所示.
(1)c+b 0,a+c 0,b-a 0(填“>”“<”或“=”);
(2)试化简:|b-a|+|a+c|-|c+b|.
答案提示
1.A
2.A
3.D
4.C
5.D6.D 7.A 8.D
9.D
10.B
11.
5
-.
12.(2a+3b)
13.2
14.4n-2或2+4(n-1)
15.2a+5b
16.a2-b2
17.4
18.
解:(1)原式=-4n2+mn+2.
(2)原式=7a-5b-c.
20.(1)解:原式=-a2b+3ab2-a2b-4ab2+2a2b=-ab2.
当a=-1,b=-2时,
原式=-(-1)×(-2)2=4.
(2)
解:原式=6a2-6ab-12b2-6a2+12b2=-6ab.
当a=-,b=-8时,
原式=-6×(-)×(-8)=-24.
21.解:原式=3a2b-2ab2+4a-4a2b+6a+2ab2+a2b-1
=10a-1,
当a=-2时,原式=10×(-2)-1=-21.
因为化简后的结果中不再含有字母b,故最后的结果与b的取值无关,b=2
016这个条件是多余的.
所以盈盈的说法是正确的.
22.
解:(1)根据题意,得40(a+b)+60(a+b)×80%=88a+88b(元),
则销售100件这种商品的总售价为(88a+88b)元.
(2)根据题意,得88a+88b-100a=-12a+88b(元),
则销售100件这种商品共盈利了(-12a+88b)元.
23.解:(1)由题意,得3x+6y+6x+3y=9x+9y,则小红和小明买这些笔记本和圆珠笔一共花费了(9x+9y)元.
(2)由题意,得(6x+3y)-(3x+6y)=3x-3y.
因为每本笔记本比每支圆珠笔贵2元,即x-y=2,所以3x-3y=3(x-y)=6(元),则小明比小红多花费了6元钱.
24.解:(1)29后面的第一个数是37.
(2)由题意,得a2-a1=2,a3-a2=3,a4-a3=4,…,由此推算a100-a99=100.
(3)a100=2+2+3+4+…+100
=1+×100=5
051.
25.解:(1)< < >(3分)
(2)原式=b-a-(a+c)+(c+b)=b-a-a-c+c+b=2b-2a.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
