北师大版数学七年级上册3.5 探索与表达规律课件(20张ppt)
文档属性
| 名称 | 北师大版数学七年级上册3.5 探索与表达规律课件(20张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 16:39:30 | ||
图片预览






文档简介
探索与表达规律
一只青蛙 1 张嘴,2 只眼睛 4 条腿,1 声扑通跳下水;
两只青蛙 2 张嘴,4 只眼睛 8 条腿,2 声扑通跳下水;
三只青蛙 3 张嘴,6 只眼睛 12 条腿,3 声扑通跳下水;
n只青蛙_____张嘴,_______只眼睛_______条腿,_______声扑通跳下水;
你能用字母
表示这首儿歌吗?
n
2n
4n
n
你能找出规律吗?
如图,你能说出第(5)幅图有多少个圆吗?第n幅图呢?
52
n2
(1)
(2)
(3)
(4)
(5)
这是2004 年12月的 日历,你能发现日历中的数字有什么规律吗?
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
请找出同一直线上三个相邻数之间的关系:
横行三个相邻数的关系
规律一:
a-1
a
a+1
探究活动一:
能用字母表示吗?
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
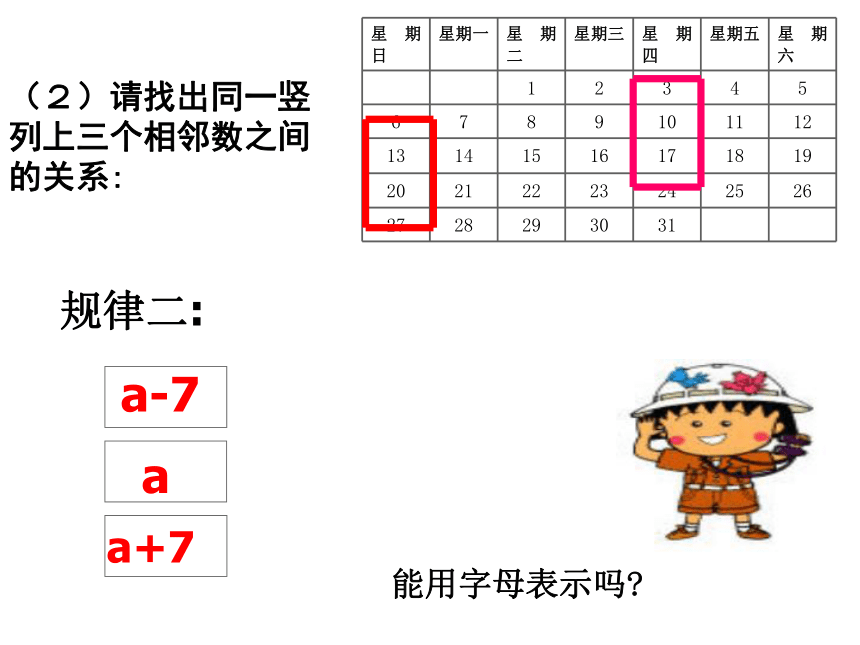
规律二:
a
a-7
a+7
能用字母表示吗?
(2)请找出同一竖列上三个相邻数之间的关系:
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
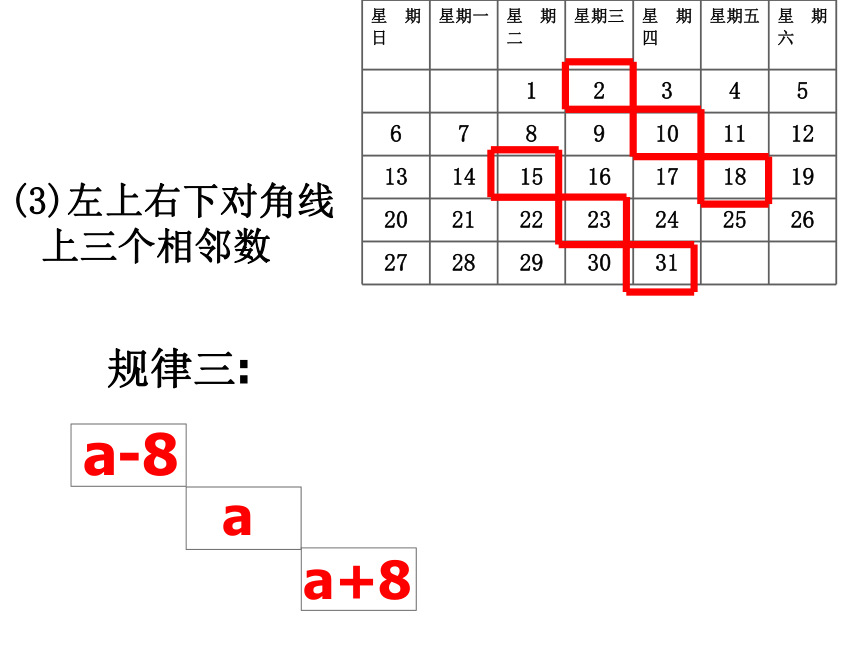
(3)左上右下对角线上三个相邻数
a
a+8
规律三:
a-8
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
规律四:
a-6
a
a+6
(4)左下右上对角线上三个相邻数
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
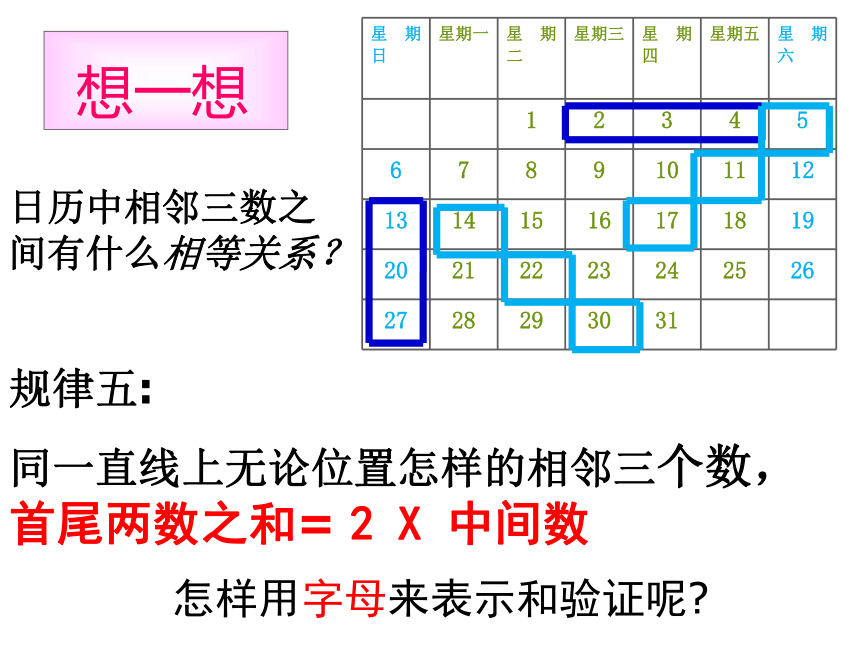
日历中相邻三数之间有什么相等关系?
规律五:
同一直线上无论位置怎样的相邻三个数, 首尾两数之和= 2 X 中间数
怎样用字母来表示和验证呢?
想一想
(1) 水平三邻数:
a-1
a
a+1
(2)竖直三邻数:
a
a-7
a+7
(3)斜下三邻数:
a
a+8
a-8
(4)斜上三邻数
a-6
a
a+6
(a-1)+(a+1)=___
2a
(a-7)+(a+7)
=____
2a
(a-8)+(a+8)=____
2a
(a-6)+(a+6)=_____
2a
在日历中,同一直线上无论位置怎样的相邻三个数,首尾两数之和都等于中间数的2倍。
注意哦! 对探索到的规律既要能用文字叙述它,又要会用字母来表示和验证它!
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(1) 日历中3×3方框内九数之和与方框中正中间的数有何等量关系?
规律六: 正方形方框中 九数之和=9×中间数
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
这个关系在其它方框中成立吗?
规律六: 九数之和=9 X 中间数
答:成立!
探究活动二
用火柴棒按下图的方式搭三角形
(2)照这样的规律搭下去,搭n个这样的
三角形需要多少根火柴棒?
(1)填写下表:
三角形个数 1 2 3 4 5
火柴棒根数
搭n个这样的三角形需要 (2n+1) 根火柴棒
3
11
9
5
7
对折次数
1
2
3
4
…
n
所得层数
折痕条数
将一张普通的报纸对折,可得到一条折痕。继续对折,对折时每次折痕与上次的折痕保持平行。连续对折4次后,可以得到几条折痕?如果对折10次呢?对折n次呢?
2
4
8
16
2n
2n -1
7
3
1
15
…
…
探究活动三
按左图方式摆放餐桌和椅子
(1) 1张餐桌可坐___人;
2张餐桌可坐___人.
(2) 按照左图的方式继续排列餐桌,完成下表:
桌子张数
1
2
3
4
5
n
可坐人数
6
10
14
18
22
4n+2
6
10
摆一摆:
(1) 2张桌子拼在一起可坐多少人?
3张桌子呢?
n张桌子呢?
一家餐厅有40张这样的长方形桌子,按照上图方式 每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐____人.
(3) 在(2)中,若改成每8张桌子拼成1张大桌子,则共可 坐____人.
1张长方形桌子可坐6人,按下图方式将桌子拼在一起.
10人
6人
8人
(2n+4)人
112
100
小 结
通过具体数值发现规律
用字母来表示规律
符号运算验证规律
观察分析对比概括
通过本节课你有哪些收获?
你会做吗?
1、完成表格内容:
类 别
四棱柱
五棱柱
十棱柱
…
n棱柱
顶点数
…
棱 数
…
面 数
…
8
12
6
10
15
7
20
30
12
2n
3n
n+2
2.研究下列算式,你发现了什么规律?用字母表示这个规律。
1×5+4=9=3×3;
2×6+4=16=4×4;
3×7+4=25=5×5;
4×8+4=36=6×6;
………………
用n表示自然数,规律是: 。
想一想
n(n+4)+4=(n+2)2
一只青蛙 1 张嘴,2 只眼睛 4 条腿,1 声扑通跳下水;
两只青蛙 2 张嘴,4 只眼睛 8 条腿,2 声扑通跳下水;
三只青蛙 3 张嘴,6 只眼睛 12 条腿,3 声扑通跳下水;
n只青蛙_____张嘴,_______只眼睛_______条腿,_______声扑通跳下水;
你能用字母
表示这首儿歌吗?
n
2n
4n
n
你能找出规律吗?
如图,你能说出第(5)幅图有多少个圆吗?第n幅图呢?
52
n2
(1)
(2)
(3)
(4)
(5)
这是2004 年12月的 日历,你能发现日历中的数字有什么规律吗?
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
请找出同一直线上三个相邻数之间的关系:
横行三个相邻数的关系
规律一:
a-1
a
a+1
探究活动一:
能用字母表示吗?
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
规律二:
a
a-7
a+7
能用字母表示吗?
(2)请找出同一竖列上三个相邻数之间的关系:
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(3)左上右下对角线上三个相邻数
a
a+8
规律三:
a-8
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
规律四:
a-6
a
a+6
(4)左下右上对角线上三个相邻数
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
日历中相邻三数之间有什么相等关系?
规律五:
同一直线上无论位置怎样的相邻三个数, 首尾两数之和= 2 X 中间数
怎样用字母来表示和验证呢?
想一想
(1) 水平三邻数:
a-1
a
a+1
(2)竖直三邻数:
a
a-7
a+7
(3)斜下三邻数:
a
a+8
a-8
(4)斜上三邻数
a-6
a
a+6
(a-1)+(a+1)=___
2a
(a-7)+(a+7)
=____
2a
(a-8)+(a+8)=____
2a
(a-6)+(a+6)=_____
2a
在日历中,同一直线上无论位置怎样的相邻三个数,首尾两数之和都等于中间数的2倍。
注意哦! 对探索到的规律既要能用文字叙述它,又要会用字母来表示和验证它!
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(1) 日历中3×3方框内九数之和与方框中正中间的数有何等量关系?
规律六: 正方形方框中 九数之和=9×中间数
星期日
星期一
星期二
星期三
星期四
星期五
星期六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
这个关系在其它方框中成立吗?
规律六: 九数之和=9 X 中间数
答:成立!
探究活动二
用火柴棒按下图的方式搭三角形
(2)照这样的规律搭下去,搭n个这样的
三角形需要多少根火柴棒?
(1)填写下表:
三角形个数 1 2 3 4 5
火柴棒根数
搭n个这样的三角形需要 (2n+1) 根火柴棒
3
11
9
5
7
对折次数
1
2
3
4
…
n
所得层数
折痕条数
将一张普通的报纸对折,可得到一条折痕。继续对折,对折时每次折痕与上次的折痕保持平行。连续对折4次后,可以得到几条折痕?如果对折10次呢?对折n次呢?
2
4
8
16
2n
2n -1
7
3
1
15
…
…
探究活动三
按左图方式摆放餐桌和椅子
(1) 1张餐桌可坐___人;
2张餐桌可坐___人.
(2) 按照左图的方式继续排列餐桌,完成下表:
桌子张数
1
2
3
4
5
n
可坐人数
6
10
14
18
22
4n+2
6
10
摆一摆:
(1) 2张桌子拼在一起可坐多少人?
3张桌子呢?
n张桌子呢?
一家餐厅有40张这样的长方形桌子,按照上图方式 每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐____人.
(3) 在(2)中,若改成每8张桌子拼成1张大桌子,则共可 坐____人.
1张长方形桌子可坐6人,按下图方式将桌子拼在一起.
10人
6人
8人
(2n+4)人
112
100
小 结
通过具体数值发现规律
用字母来表示规律
符号运算验证规律
观察分析对比概括
通过本节课你有哪些收获?
你会做吗?
1、完成表格内容:
类 别
四棱柱
五棱柱
十棱柱
…
n棱柱
顶点数
…
棱 数
…
面 数
…
8
12
6
10
15
7
20
30
12
2n
3n
n+2
2.研究下列算式,你发现了什么规律?用字母表示这个规律。
1×5+4=9=3×3;
2×6+4=16=4×4;
3×7+4=25=5×5;
4×8+4=36=6×6;
………………
用n表示自然数,规律是: 。
想一想
n(n+4)+4=(n+2)2
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
