人教版八年级上册 数学 课件: 11.2.2三角形的外角(共26张PPT)
文档属性
| 名称 | 人教版八年级上册 数学 课件: 11.2.2三角形的外角(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 720.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 14:47:00 | ||
图片预览




文档简介
(共26张PPT)
11.2.2三角形的外角
三角形的外角
那就让我们
A
B
C
D
E
想一想
?
同学们,你们知不知道国旗上的五角星的五个角的和是多少度吗?
三角形的外角
B
A
C
D
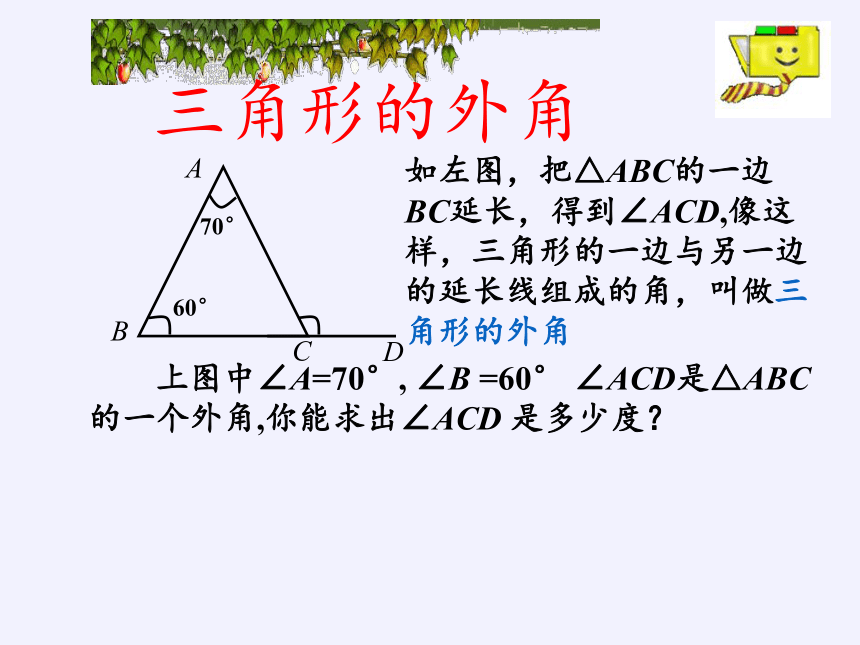
如左图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角
60°
70°
上图中∠A=70°,
∠B
=60°
∠ACD是△ABC的一个外角,你能求出∠ACD
是多少度?
画图并思考:
画一个△ABC
,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
归纳:
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个.
每个外角与相应的内角是邻补角.
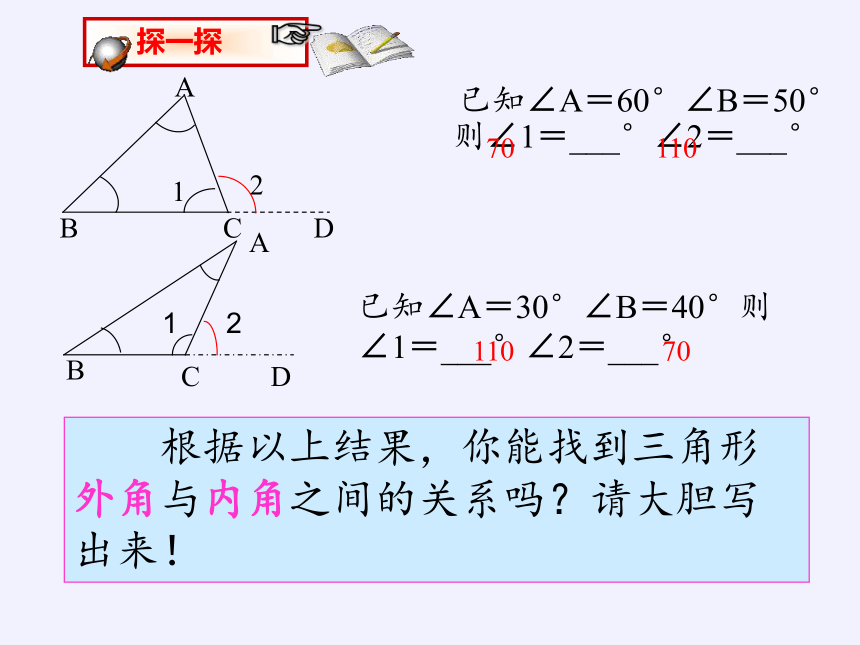
已知∠A=60°∠B=50°则∠1=___°∠2=___°
探一探
?
A
B
C
D
2
1
A
B
C
D
1
2
已知∠A=30°∠B=40°则∠1=___°∠2=___°
根据以上结果,你能找到三角形外角与内角之间的关系吗?请大胆写出来!
70
110
110
70
三角形的外角
B
A
C
D
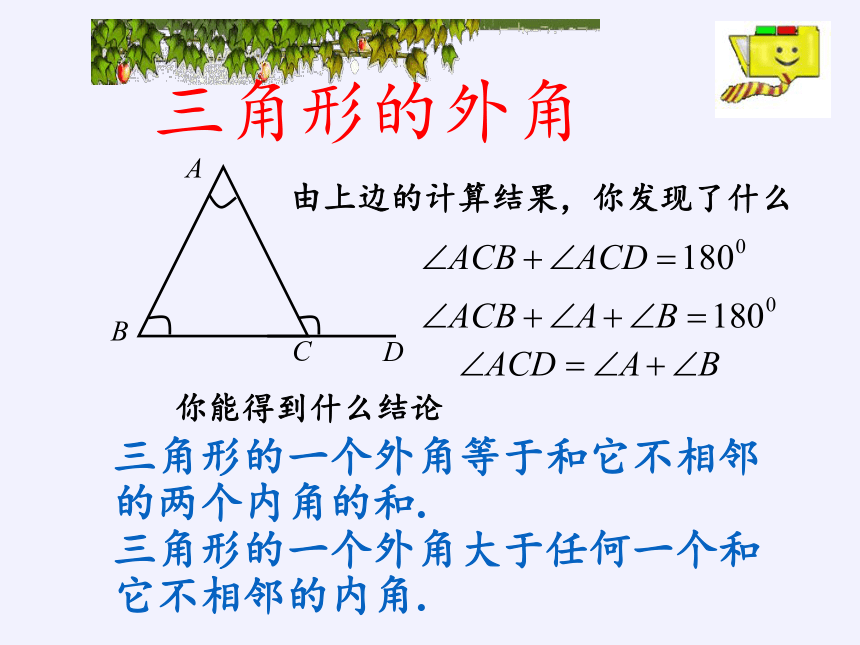
由上边的计算结果,你发现了什么
你能得到什么结论
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
1
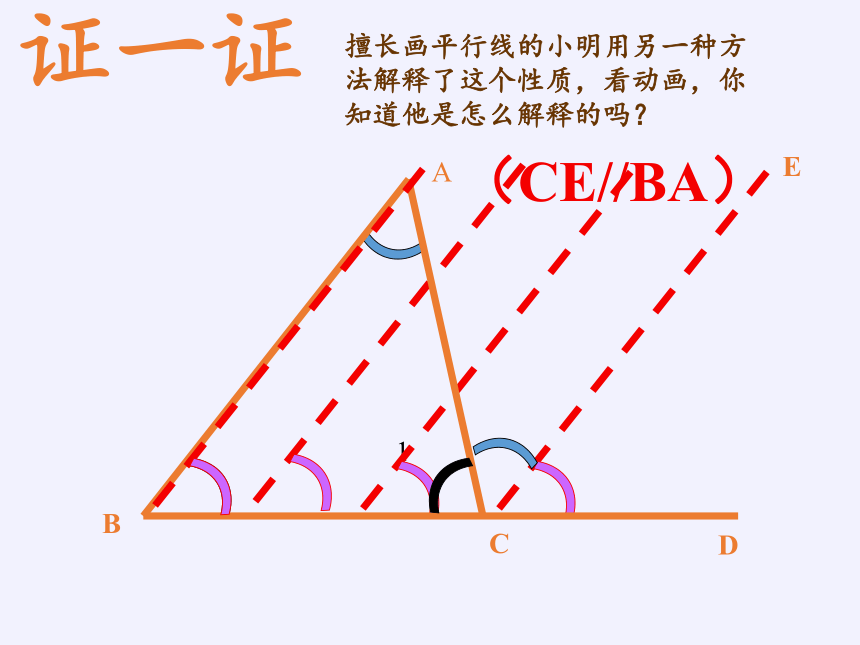
(CE//BA)
A
E
证一证
擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?
C
B
D
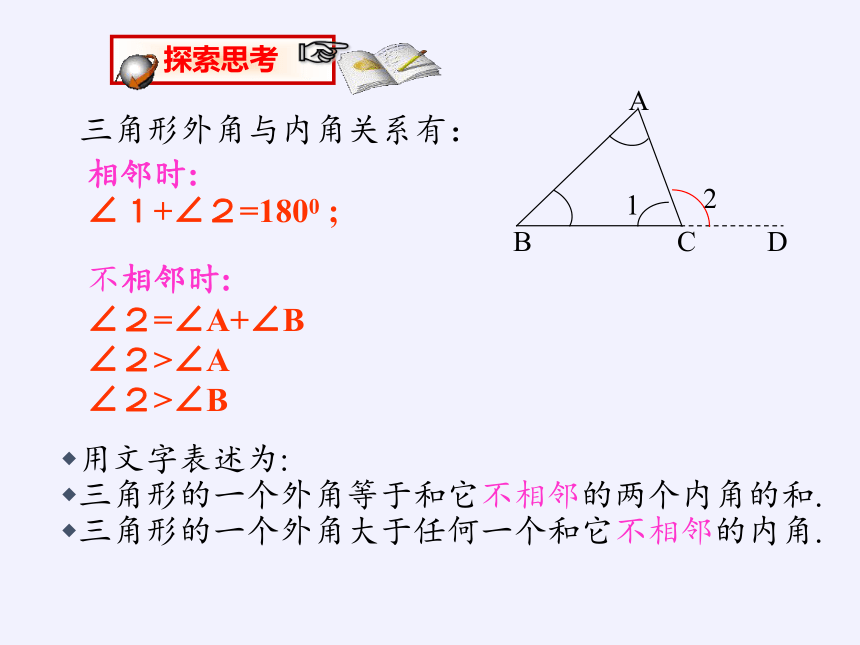
三角形外角与内角关系有:
相邻时:
∠1+∠2=1800
;
探索思考
?
用文字表述为:
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
A
B
C
D
2
1
不相邻时:
∠2=∠A+∠B
∠2>∠A
∠2>∠B
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论(corollary).
推论可以当作定理使用.
三角形内角和定理的推论:
推论1:
三角形的一个外角等于和它不相邻的两个内角的和.
推论2:
三角形的一个外角大于任何一个和它不相邻的内角.
关注▲外角
?
A
B
C
D
2
1
数学语言
推论1:
∠2=∠A+∠B.
推论2:
∠2>∠A;
∠2>∠B;
我能行
已知:如图,在△ABC中,外角∠DCA=100°,∠A=45°.
求:∠B和∠ACB的大小.
随堂练习
?
A
B
C
D
如图,D
是△ABC
的BC
边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B
的度数;
(2)∠C
的度数.
典型例题
如图:已知在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=450
,∠F=300,∠CGF=700,
求∠A的度数.
A
E
G
F
C
B
探究
如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,你能利用三角形的内角和等于1800求出这三个外角的和吗?
A
B
C
D
E
F
A
B
C
1
2
3
方法1
方法2
三角形的外角和定理:
三角形的外角和等于360°
∠1+∠2
+∠3
=
?
从哪些途径探究这个结果
议一议
A
B
C
1
2
3
∠2+
∠ABC=180°
∠3+
∠ACB=180°
三个式子相加得到
∠1+
∠2+
∠3+
∠BAC+
∠ABC+∠ACB=540°
而∠BAC+
∠ABC+∠ACB=180°
∠1+
∠2+
∠3=360°
∠1+
∠BAC=180°
解:
解:过A作AD平行于BC
∠3=
∠4
B
C
1
2
3
4
A
∠2=
∠BAD
所以,
∠1+
∠2+
∠3=
∠1+
∠4+
∠BAD=360°
两直线平行,同位角相等
D
“行家”看“门道”
已知:如右图,在△ABC中,AD平分外角∠EAC,∠B=
∠C.
求证:AD∥BC.
证明:∵
∠EAC=∠B+∠C
(三角形的一个外角等于和它不相邻的两个内角的和),
∴
AD
∥BC(内错角相等,两直线平行).
∠B=∠C
(已知),
∴∠DAC=∠C(等量代换).
A
C
D
B
E
分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”.
∵
AD平分
∠EAC(已知).
∴∠C=
∠EAC(等式性质).
∴∠DAC=
∠EAC(角平分线的定义).
·
·
例题是运用了定理“内错角相等,两直线平行”得到了证实.
已知:五角星如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个外角
∴
∠1=∠B+∠D
分析:设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
又∵∠A+∠1+∠2=180°(
?
)
又
∵
∠2是△EHC的一个外角
∴
∠2=∠C+∠E
A
B
C
D
E
F
1
H
2
∴
∠A+∠B+∠C+∠D+∠E
=180°
想一想
练一练
∠A+∠B+∠C+∠D+∠E+∠F=
.
A
D
E
C
F
B
1
2
3
360°
N
P
M
判断题:
1、三角形的外角和是指三角形所有外角的和。(
)
2、三角形的外角和等于它内角和的2倍。(
)
3、三角形的一个外角等于两个内角的和。(
)
4、三角形的一个外角等于与它不相邻的两个内角的和。(
)
5、三角形的一个外角大于任何一个内角。(
)
6、三角形的一个内角小于任何一个与它不相邻的外角。(
)
如图,类似于三角形,我们称
∠1+
∠2+
∠3+
∠4为四边形的外角和,
已知四边形的内角和为360?,你能用今
天所学的方法进行推理计算吗?能知道
多边形的外角和吗?
1
2
3
4
A
B
C
D
思考
关注三角形的外角
三角形内角和定理的推论:
推论1:
三角形的一个外角等于和它不相邻的两个内角的和.
推论2:
三角形的一个外角大于任何一个和它不相邻的内角.
△ABC中:
推论1:
∠2=∠A+∠B.
推论2:
∠2>∠A;
∠2>∠B;
小
结
?
这个结论以后可以直接运用.
A
B
C
D
2
1
再见
已知:P是△ABC内一点。
求证:∠BPC>∠BAC
A
B
C
P
D
谢
谢
11.2.2三角形的外角
三角形的外角
那就让我们
A
B
C
D
E
想一想
?
同学们,你们知不知道国旗上的五角星的五个角的和是多少度吗?
三角形的外角
B
A
C
D
如左图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角
60°
70°
上图中∠A=70°,
∠B
=60°
∠ACD是△ABC的一个外角,你能求出∠ACD
是多少度?
画图并思考:
画一个△ABC
,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
归纳:
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个.
每个外角与相应的内角是邻补角.
已知∠A=60°∠B=50°则∠1=___°∠2=___°
探一探
?
A
B
C
D
2
1
A
B
C
D
1
2
已知∠A=30°∠B=40°则∠1=___°∠2=___°
根据以上结果,你能找到三角形外角与内角之间的关系吗?请大胆写出来!
70
110
110
70
三角形的外角
B
A
C
D
由上边的计算结果,你发现了什么
你能得到什么结论
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
1
(CE//BA)
A
E
证一证
擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?
C
B
D
三角形外角与内角关系有:
相邻时:
∠1+∠2=1800
;
探索思考
?
用文字表述为:
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
A
B
C
D
2
1
不相邻时:
∠2=∠A+∠B
∠2>∠A
∠2>∠B
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论(corollary).
推论可以当作定理使用.
三角形内角和定理的推论:
推论1:
三角形的一个外角等于和它不相邻的两个内角的和.
推论2:
三角形的一个外角大于任何一个和它不相邻的内角.
关注▲外角
?
A
B
C
D
2
1
数学语言
推论1:
∠2=∠A+∠B.
推论2:
∠2>∠A;
∠2>∠B;
我能行
已知:如图,在△ABC中,外角∠DCA=100°,∠A=45°.
求:∠B和∠ACB的大小.
随堂练习
?
A
B
C
D
如图,D
是△ABC
的BC
边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B
的度数;
(2)∠C
的度数.
典型例题
如图:已知在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=450
,∠F=300,∠CGF=700,
求∠A的度数.
A
E
G
F
C
B
探究
如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,你能利用三角形的内角和等于1800求出这三个外角的和吗?
A
B
C
D
E
F
A
B
C
1
2
3
方法1
方法2
三角形的外角和定理:
三角形的外角和等于360°
∠1+∠2
+∠3
=
?
从哪些途径探究这个结果
议一议
A
B
C
1
2
3
∠2+
∠ABC=180°
∠3+
∠ACB=180°
三个式子相加得到
∠1+
∠2+
∠3+
∠BAC+
∠ABC+∠ACB=540°
而∠BAC+
∠ABC+∠ACB=180°
∠1+
∠2+
∠3=360°
∠1+
∠BAC=180°
解:
解:过A作AD平行于BC
∠3=
∠4
B
C
1
2
3
4
A
∠2=
∠BAD
所以,
∠1+
∠2+
∠3=
∠1+
∠4+
∠BAD=360°
两直线平行,同位角相等
D
“行家”看“门道”
已知:如右图,在△ABC中,AD平分外角∠EAC,∠B=
∠C.
求证:AD∥BC.
证明:∵
∠EAC=∠B+∠C
(三角形的一个外角等于和它不相邻的两个内角的和),
∴
AD
∥BC(内错角相等,两直线平行).
∠B=∠C
(已知),
∴∠DAC=∠C(等量代换).
A
C
D
B
E
分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”.
∵
AD平分
∠EAC(已知).
∴∠C=
∠EAC(等式性质).
∴∠DAC=
∠EAC(角平分线的定义).
·
·
例题是运用了定理“内错角相等,两直线平行”得到了证实.
已知:五角星如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△BDF的一个外角
∴
∠1=∠B+∠D
分析:设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.
又∵∠A+∠1+∠2=180°(
?
)
又
∵
∠2是△EHC的一个外角
∴
∠2=∠C+∠E
A
B
C
D
E
F
1
H
2
∴
∠A+∠B+∠C+∠D+∠E
=180°
想一想
练一练
∠A+∠B+∠C+∠D+∠E+∠F=
.
A
D
E
C
F
B
1
2
3
360°
N
P
M
判断题:
1、三角形的外角和是指三角形所有外角的和。(
)
2、三角形的外角和等于它内角和的2倍。(
)
3、三角形的一个外角等于两个内角的和。(
)
4、三角形的一个外角等于与它不相邻的两个内角的和。(
)
5、三角形的一个外角大于任何一个内角。(
)
6、三角形的一个内角小于任何一个与它不相邻的外角。(
)
如图,类似于三角形,我们称
∠1+
∠2+
∠3+
∠4为四边形的外角和,
已知四边形的内角和为360?,你能用今
天所学的方法进行推理计算吗?能知道
多边形的外角和吗?
1
2
3
4
A
B
C
D
思考
关注三角形的外角
三角形内角和定理的推论:
推论1:
三角形的一个外角等于和它不相邻的两个内角的和.
推论2:
三角形的一个外角大于任何一个和它不相邻的内角.
△ABC中:
推论1:
∠2=∠A+∠B.
推论2:
∠2>∠A;
∠2>∠B;
小
结
?
这个结论以后可以直接运用.
A
B
C
D
2
1
再见
已知:P是△ABC内一点。
求证:∠BPC>∠BAC
A
B
C
P
D
谢
谢
