人教版八年级上册数学12.2全等三角形判定解答题专项练习(Word版含答案)
文档属性
| 名称 | 人教版八年级上册数学12.2全等三角形判定解答题专项练习(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 221.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 15:30:37 | ||
图片预览

文档简介
12.2全等三角形判定解答题专项练习
1.阅读探索题:
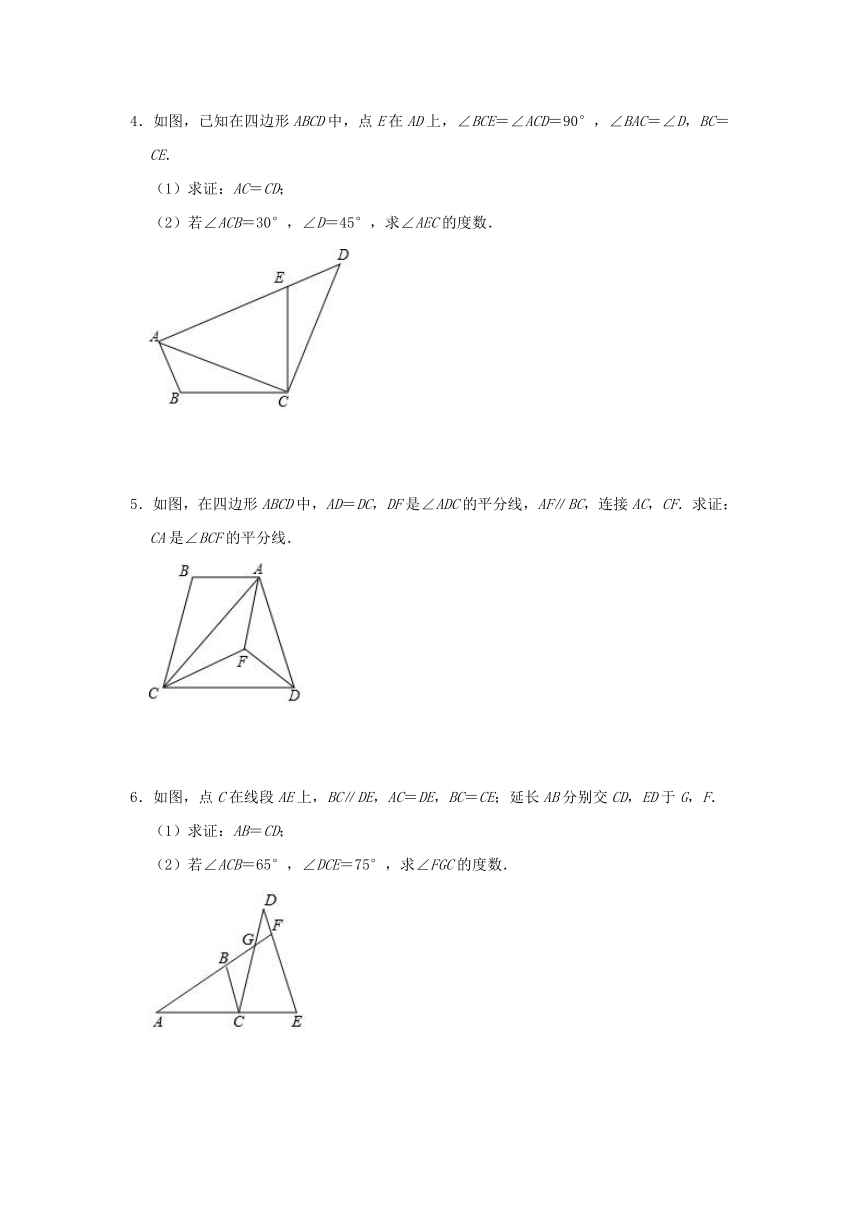
(1)如图1,OP是∠MON的平分线,以O为圆心任意长为半径作弧,分别交射线ON、OM于C、B两点,在射线OP上任取一点A(点O除外),连接AB、AC.求证:△AOB≌△AOC.
(2)请你参考以上方法,解答下列问题:
如图2,在
Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系并证明.
2.已知:如图,AC、BD相交于点O,AC=BD,AB=CD.
(1)求证:∠A=∠D;
(2)若OC=2,求OB的长.
3.已知,如图所示,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F.H是BC边上的中点,连接DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=BF;
(3)请你根据该题的条件并结合图形,自己提出一个问题,并解答或证明你提出的问题.
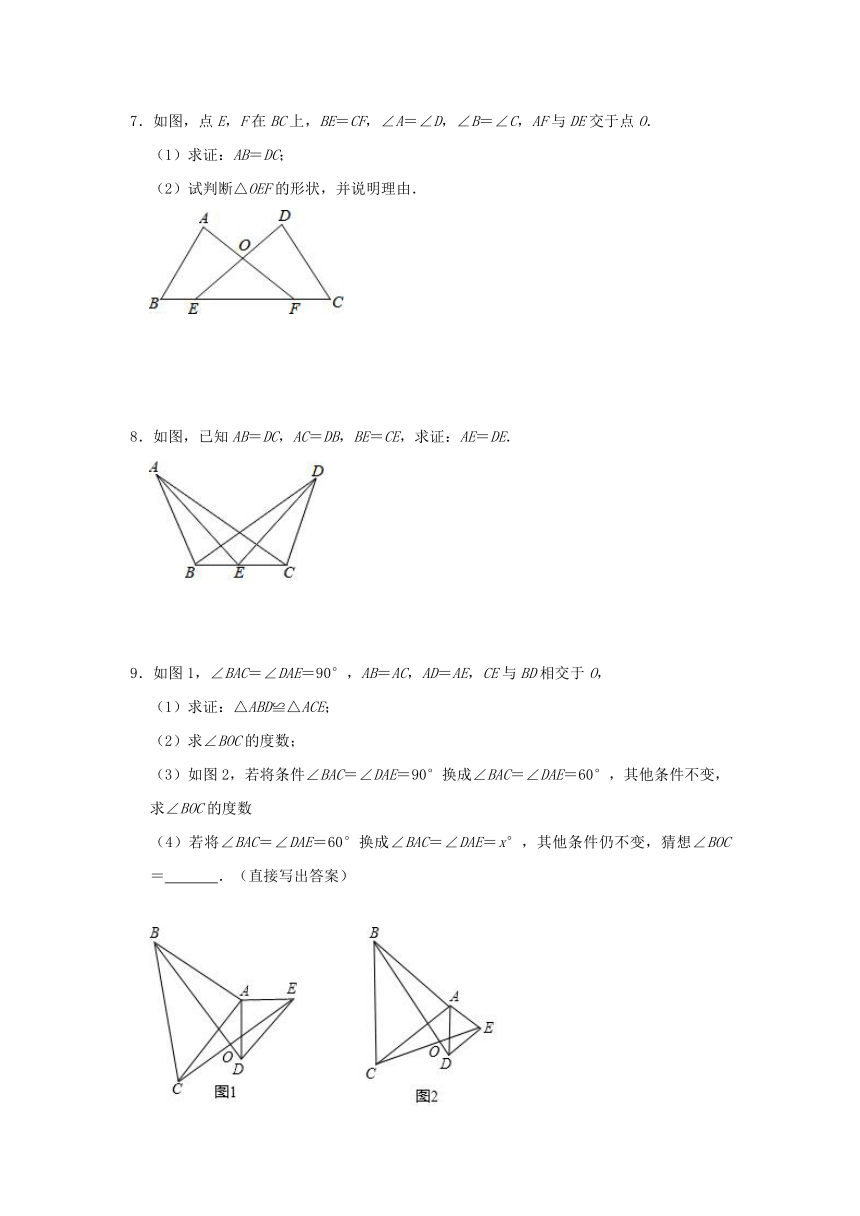
4.如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若∠ACB=30°,∠D=45°,求∠AEC的度数.
5.如图,在四边形ABCD中,AD=DC,DF是∠ADC的平分线,AF∥BC,连接AC,CF.求证:CA是∠BCF的平分线.
6.如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE;延长AB分别交CD,ED于G,F.
(1)求证:AB=CD;
(2)若∠ACB=65°,∠DCE=75°,求∠FGC的度数.
7.如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
8.如图,已知AB=DC,AC=DB,BE=CE,求证:AE=DE.
9.如图1,∠BAC=∠DAE=90°,AB=AC,AD=AE,CE与BD相交于O,
(1)求证:△ABD≌△ACE;
(2)求∠BOC的度数;
(3)如图2,若将条件∠BAC=∠DAE=90°换成∠BAC=∠DAE=60°,其他条件不变,求∠BOC的度数
(4)若将∠BAC=∠DAE=60°换成∠BAC=∠DAE=x°,其他条件仍不变,猜想∠BOC=
.(直接写出答案)
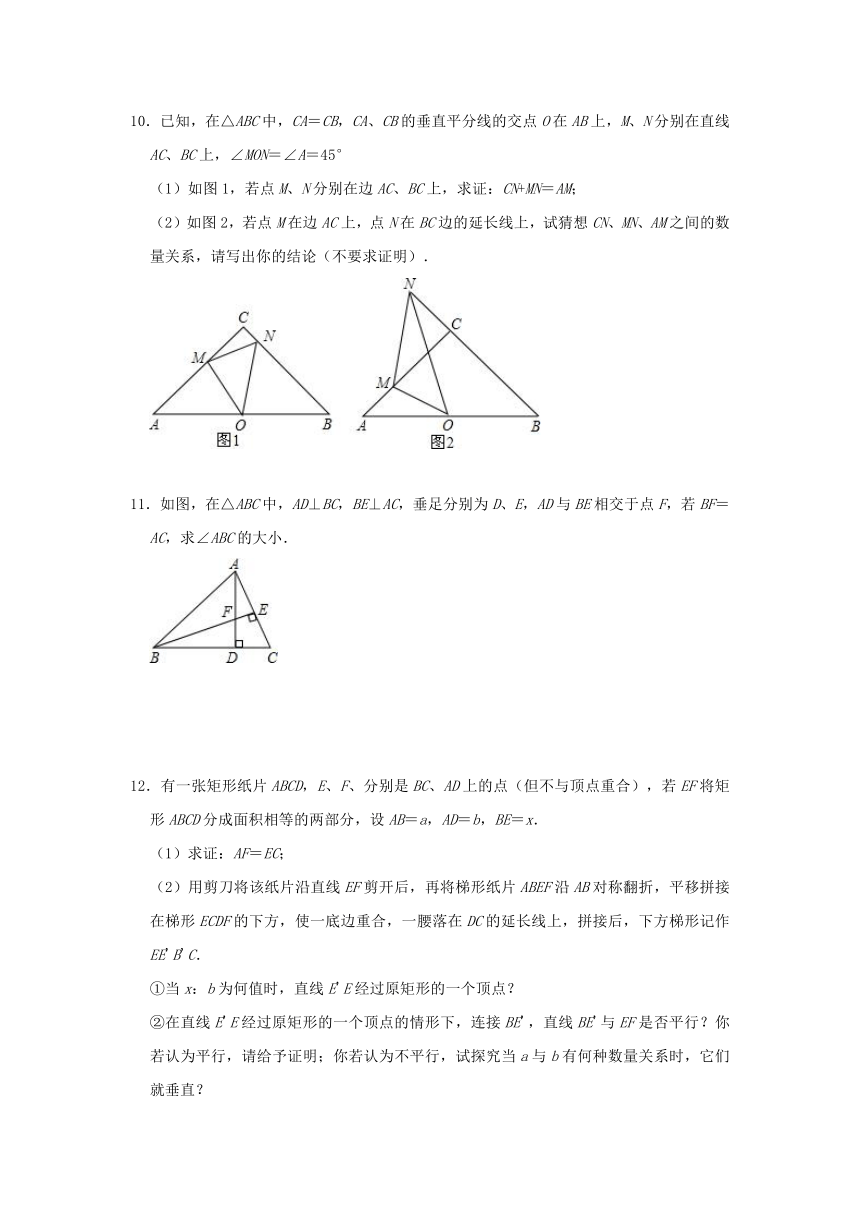
10.已知,在△ABC中,CA=CB,CA、CB的垂直平分线的交点O在AB上,M、N分别在直线AC、BC上,∠MON=∠A=45°
(1)如图1,若点M、N分别在边AC、BC上,求证:CN+MN=AM;
(2)如图2,若点M在边AC上,点N在BC边的延长线上,试猜想CN、MN、AM之间的数量关系,请写出你的结论(不要求证明).
11.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F,若BF=AC,求∠ABC的大小.
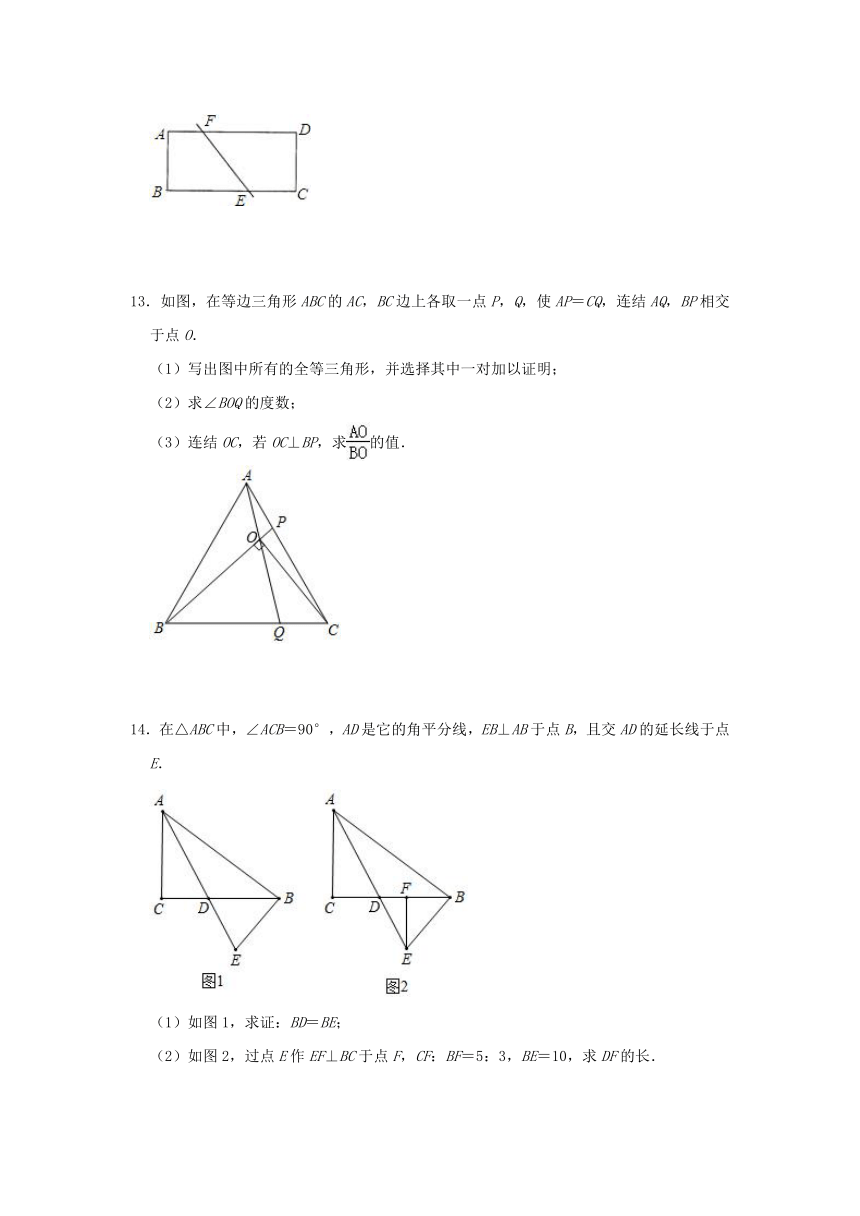
12.有一张矩形纸片ABCD,E、F、分别是BC、AD上的点(但不与顶点重合),若EF将矩形ABCD分成面积相等的两部分,设AB=a,AD=b,BE=x.
(1)求证:AF=EC;
(2)用剪刀将该纸片沿直线EF剪开后,再将梯形纸片ABEF沿AB对称翻折,平移拼接在梯形ECDF的下方,使一底边重合,一腰落在DC的延长线上,拼接后,下方梯形记作EE'B'C.
①当x:b为何值时,直线E'E经过原矩形的一个顶点?
②在直线E'E经过原矩形的一个顶点的情形下,连接BE',直线BE'与EF是否平行?你若认为平行,请给予证明;你若认为不平行,试探究当a与b有何种数量关系时,它们就垂直?
13.如图,在等边三角形ABC的AC,BC边上各取一点P,Q,使AP=CQ,连结AQ,BP相交于点O.
(1)写出图中所有的全等三角形,并选择其中一对加以证明;
(2)求∠BOQ的度数;
(3)连结OC,若OC⊥BP,求的值.
14.在△ABC中,∠ACB=90°,AD是它的角平分线,EB⊥AB于点B,且交AD的延长线于点E.
(1)如图1,求证:BD=BE;
(2)如图2,过点E作EF⊥BC于点F,CF:BF=5:3,BE=10,求DF的长.
15.图1,在△ABC中,BD是∠ABC的平分线,请你利用该图形构造一个以BD所在直线为对称轴且与△ABD全等的三角形
(1)如图2,在△ABC中,∠A=100°,∠C=50°,BD是∠ABC的角平分线,请你判断并写出AB、AD、BC之间的数量关系
(2)如图3,在△ABC中,∠C=40°,而(1)中的其他条件不变,请你判断AD、BD、BC之间的数量关系并证明.
参考答案
1.(1)证明:在△AOB和△AOC中,,
∴△AOB≌△AOC(SAS).
(2)在CB上截取CE=CA,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
在△ACD和△ECD中,,
∴△ACD≌△ECD(SAS),
∴∠CAD=∠CED=60°,
∵∠ACB=90°,
∴∠B=30°,
∴∠EDB=30°,
即∠EDB=∠B,
∴DE=EB,
∵BC=CE+BE,
∴BC=AC+DE,
∴BC=AC+AD.
2.(1)证明:在△ABC与△DCB中,
,
∴△ABC≌△DCB(SSS);
∴∠A=∠D;
(2)由(1)知∠A=∠D,
在△AOB与△DOC中,
,
∴△AOB≌△DOC(AAS),
∴OB=OC,
∵OC=2,
∴OB=OC=2.
3.证明:(1)∵∠ABC=45°,CD⊥AB于D,
∴△BCD是等腰直角三角形,H是BC边的中点,
∴BD=CD,
∵CD⊥AB于D,BE⊥AC于E,
∴∠DBF+∠A=90°,∠ACD+∠A=90°,
∴∠DBF=∠ACD,
在△BDF与△CDA中,
,
∴△BDF≌△CDA(ASA),
∴BF=AC;
(2)∵BE平分∠ABC,且BE⊥AC于E,
∴∠ABE=∠CBE,∠AEB=∠CEB=90°,
∴在△ABE与△CBE中,
,
∴△ABE≌△CBE(ASA),
∴AE=CE=AC,
∴BF=2CE,
即CE=BF;
(3)提出问题是连接DE,则∠DEB=45°,
证明如下:
∵∠CEB=∠CDB=90°,∴C,B,D,E四点共圆,
∴∠DEB=∠CDB=45°,
4.解:∵∠BCE=∠ACD=90°,
∴∠3+∠4=∠4+∠5,
∴∠3=∠5,
在△ABC和△DEC中,,
∴△ABC≌△DEC(AAS),
∴AC=CD;
(2)∵∠ACD=90°,AC=CD,
∴∠2=∠D=45°,
∵∠ACB=30°,∠BCE=∠ACD=90°,
∴∠4=60°,
∴∠AEC=180°﹣45°﹣60°=75°.
5.证明:∵DF是∠ADC的平分线,
∴∠CDF=∠ADF.
又∵AD=DC,DF=DF,
在△ADF与△CDF中,
,
∴△ADF≌△CDF,
∴AF=CF,
∴∠ACF=∠CAF.
∵AF∥CB,
∴∠CAF=∠ACB,
∴∠ACF=∠ACB,即CA平分∠BCF
6.证明:(1)∵BC∥DE,
∴∠ACB=∠CED,
在△ABC与△DCE中
,
∴△ABC≌△DCE(SAS),
∴AB=CD;
(2)∵△ABC≌△DCE,
∴∠A=∠D,∠ABC=∠DCE=75°,
∵∠ACB=65°,
∴∠A=∠D=180°﹣75°﹣65°=40°,
∴∠FBC=∠A+∠ACB=40°+65°=105°,
∵BC∥DE,
∴∠DFB=∠FBC=105°,
∴∠FGC=∠D+∠DFB=40°+105°=145°.
7.(1)证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE.
又∵∠A=∠D,∠B=∠C,
在△ABF与△DCE中,
,
∴△ABF≌△DCE(AAS),
∴AB=DC.
(2)△OEF为等腰三角形
理由如下:∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF,
∴△OEF为等腰三角形.
8.证明:在△ABC和△DCB中,
,
∴△ABC≌△DCB(SSS).
∴∠ABC=∠DCB.
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS).
∴AE=DE.
9.(1)证明:∵∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE,
(2)解:如图1中,设AC交BD于H.
∵△BAD≌△CAE,
∴∠HCO=∠HBA,
∵∠BHA=∠CHO,
∴∠COH=∠HAB=90°.
(3)如图2中,易证△BAD≌△CAE,
∴∠HCO=∠HBA,
∵∠BHA=∠CHO,
∴∠COH=∠HAB=60°.
(4)同法可证△BAD≌△CAE,
∴∠HCO=∠HBA,
∵∠BHA=∠CHO,
∴∠COH=∠HAB=x°.
故答案为x°.
10.解:(1)连接OC,在AM上截取AQ=CN,连接OQ,
∵O为CA、CB的垂直平分线的交点,
∴OC=OA=OB,
∵AC=BC,∴OC⊥AB,CO平分∠ACB,
∴∠A=∠B=45°,即∠ACB=90°,
∴∠OCN=45°,即∠OCN=∠A=45°,
在△AOQ和△CON中,
,
∴△AOQ≌△CON(SAS),
∴OQ=ON,∠AOQ=∠CON,
∵OC⊥AB,
∴∠AOC=∠AOQ+∠COQ=90°,
∴∠CON+∠COQ=90°,即∠QON=90°,
又∠MON=45°,
∴∠QOM=45°,
在△QOM和△NOM中,
∴△QOM≌△NOM(SAS),
∴QM=NM,
则AM=AQ+QM=CN+MN;
(2)MN=AM+CN.
11.解:∵AD⊥BC,BE⊥AC(已知),
∴∠ADB=∠ADC=∠BEC=90°(垂直定义),
又∵∠AFE=∠BFD(对顶角相等),
∴△AEF∽△BDF(两对对应角相等的两三角形相似),
∴∠FAE=∠FBD(相似三角形的对应角相等),
在△BFD和△ACD中,
,
∴△BFD≌△ACD(AAS),
∴BD=AD(全等三角形的对应边相等),
∴∠BAD=∠ABD(等边对等角),
又∵∠ADB=90°(已证),
∴∠ABC==45°(三角形的内角和定理).
12.解:(1)证明:由(x+AF)?a=(b﹣x+b﹣AF)?a,
得AF=b﹣x,
又EC=b﹣x,
∴AF=EC.
(2)翻折后的图形如图,
①如图1,当直线EE′经过原矩形顶点D时,x:b=,
如图2,当直线E′E经过原矩形的顶点A时,x:b=;
②如图1,当矩形E′E经过原矩形顶点D时,BE′∥EF,
理由如下:根据题意得,BE=DF,EE′=EF,
又∵∠BEE′=∠DEC=∠EDF,
∴在△BEE′与△FDE中,
,
∴△BEE′≌△FED(SAS),
∴∠BE′E=∠FED,
∴BE′∥EF;
如图2,当直线E′E经过原矩形的顶点A时,且当a:b=时,BE′与EF垂直.
13.解:(1)△ABP≌△ACQ,△ABQ≌△BCP
证明△ABP≌△ACQ
∵△ABC是等边三角形
∴∠BAP=∠ACQ=∠ABQ,AB=AC=BC
∵在△ABP和△ACQ中
∴△ABP≌△ACQ
(SAS)
(2)∵△ABP≌△ACQ
∴∠ABP=∠CAQ,∠BAQ+∠CAQ=60°
∴∠BAQ+∠ABP=60°
∵∠BOQ=∠BAQ+ABP
∴∠BOQ=60°.
(3)
如图所示,过点B作BD⊥AQ交AQ于点D
由(1)知△ABQ≌△BCP(SAS)
∴∠BAD=∠OBC
∴在△ABD和△BCO中
∴△ABD≌△BCO
(AAS)
∴AD=BO
在Rt△BOD中,∠BOD=60°,∠OBD=30°
∴BO=2OD
∴AD=2OD
∴点O为AD的中点
∴=
∴=.
14.证明:(1)如图1所示:
∵AD是∠BAC的角平分线,
∴∠BAD=∠CAD,
又∵EB⊥AB,
∴∠ABE=90°,
∴∠BAE+∠E=90°,
又∵∠CAD+∠ADC=90°,
∴∠ADC=∠E,
又∵∠ADC=∠BDE,
∴∠BDE=∠E,
∴BD=BE;
(2)过点D作DH⊥AB于H,设CF=5x,如图2所示:
∵∠ACB=90°,∴CD⊥AC,
又∵DH⊥AB,AD是∠BAC的角平分线,
∴CD=DH,
又∵EF⊥BD∴∠BFE=90°,
∴∠FEB+∠FBE=90°,
又∵∠ABC+∠FBE=90,
∴∠HBD=∠FEB,
∵DH⊥AB,∴∠BHD=90°,
∴∠BFE=∠BHD=90°,
在△BHD和△EBF中,
∴,
∴△BHD≌△EBF(AAS),
∴DH=BF,
∴CD=BF
∵CF:BF=5:3
∵CF=5x,∴BF=3x,CD=3x,
∴DF=CF﹣CD=5x﹣3x=2x,
∴BD=BF+DF=3x+2x═5x,
∵BE=10,
∴5x=10,x=2,
∴DF=4.
15.解:作出全等图形得(1分)
(1)BC=AB+AD…(2分)
(2)BC=BD+AD
证明:方法一:
在BC上截取BE=AB,连接DE,在BC上截取BF=BD,连接DF…(3分)
∵BD平分∠ABC,∴∠ABD=∠CBD
在△ABD和△EBD中
AB=BE
∠ABD=∠CBD
BD=BD
∴△ABD≌△EBD,
∴AD=DE…(4分)
∠DEB=∠A=100°
∴∠DEC=80°,
∵∠A=100°,∠C=40°
∴∠ABC=40°
∵BD平分∠ABC,
∴∠ABD=∠CBD=20°
∵BD=BF,
∴∠BFD=80°
∠DEC=∠BFD=80°,
∴DE=DF…(5分)
∵∠DFB=80°,∠C=40°
∴∠CDF=40°,
∴DF=CF
∴AD=CF
∴BC=BF+CF=BD+AD…(7分)
方法二:延长BD到F,使DF=AD,在BC上
截取BE=AB,通过证△ABE≌△DBE和
△CDF≌△CDE得到AD=DF;再证明BC=BF.
1.阅读探索题:
(1)如图1,OP是∠MON的平分线,以O为圆心任意长为半径作弧,分别交射线ON、OM于C、B两点,在射线OP上任取一点A(点O除外),连接AB、AC.求证:△AOB≌△AOC.
(2)请你参考以上方法,解答下列问题:
如图2,在
Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系并证明.
2.已知:如图,AC、BD相交于点O,AC=BD,AB=CD.
(1)求证:∠A=∠D;
(2)若OC=2,求OB的长.
3.已知,如图所示,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F.H是BC边上的中点,连接DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=BF;
(3)请你根据该题的条件并结合图形,自己提出一个问题,并解答或证明你提出的问题.
4.如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若∠ACB=30°,∠D=45°,求∠AEC的度数.
5.如图,在四边形ABCD中,AD=DC,DF是∠ADC的平分线,AF∥BC,连接AC,CF.求证:CA是∠BCF的平分线.
6.如图,点C在线段AE上,BC∥DE,AC=DE,BC=CE;延长AB分别交CD,ED于G,F.
(1)求证:AB=CD;
(2)若∠ACB=65°,∠DCE=75°,求∠FGC的度数.
7.如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
8.如图,已知AB=DC,AC=DB,BE=CE,求证:AE=DE.
9.如图1,∠BAC=∠DAE=90°,AB=AC,AD=AE,CE与BD相交于O,
(1)求证:△ABD≌△ACE;
(2)求∠BOC的度数;
(3)如图2,若将条件∠BAC=∠DAE=90°换成∠BAC=∠DAE=60°,其他条件不变,求∠BOC的度数
(4)若将∠BAC=∠DAE=60°换成∠BAC=∠DAE=x°,其他条件仍不变,猜想∠BOC=
.(直接写出答案)
10.已知,在△ABC中,CA=CB,CA、CB的垂直平分线的交点O在AB上,M、N分别在直线AC、BC上,∠MON=∠A=45°
(1)如图1,若点M、N分别在边AC、BC上,求证:CN+MN=AM;
(2)如图2,若点M在边AC上,点N在BC边的延长线上,试猜想CN、MN、AM之间的数量关系,请写出你的结论(不要求证明).
11.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D、E,AD与BE相交于点F,若BF=AC,求∠ABC的大小.
12.有一张矩形纸片ABCD,E、F、分别是BC、AD上的点(但不与顶点重合),若EF将矩形ABCD分成面积相等的两部分,设AB=a,AD=b,BE=x.
(1)求证:AF=EC;
(2)用剪刀将该纸片沿直线EF剪开后,再将梯形纸片ABEF沿AB对称翻折,平移拼接在梯形ECDF的下方,使一底边重合,一腰落在DC的延长线上,拼接后,下方梯形记作EE'B'C.
①当x:b为何值时,直线E'E经过原矩形的一个顶点?
②在直线E'E经过原矩形的一个顶点的情形下,连接BE',直线BE'与EF是否平行?你若认为平行,请给予证明;你若认为不平行,试探究当a与b有何种数量关系时,它们就垂直?
13.如图,在等边三角形ABC的AC,BC边上各取一点P,Q,使AP=CQ,连结AQ,BP相交于点O.
(1)写出图中所有的全等三角形,并选择其中一对加以证明;
(2)求∠BOQ的度数;
(3)连结OC,若OC⊥BP,求的值.
14.在△ABC中,∠ACB=90°,AD是它的角平分线,EB⊥AB于点B,且交AD的延长线于点E.
(1)如图1,求证:BD=BE;
(2)如图2,过点E作EF⊥BC于点F,CF:BF=5:3,BE=10,求DF的长.
15.图1,在△ABC中,BD是∠ABC的平分线,请你利用该图形构造一个以BD所在直线为对称轴且与△ABD全等的三角形
(1)如图2,在△ABC中,∠A=100°,∠C=50°,BD是∠ABC的角平分线,请你判断并写出AB、AD、BC之间的数量关系
(2)如图3,在△ABC中,∠C=40°,而(1)中的其他条件不变,请你判断AD、BD、BC之间的数量关系并证明.
参考答案
1.(1)证明:在△AOB和△AOC中,,
∴△AOB≌△AOC(SAS).
(2)在CB上截取CE=CA,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
在△ACD和△ECD中,,
∴△ACD≌△ECD(SAS),
∴∠CAD=∠CED=60°,
∵∠ACB=90°,
∴∠B=30°,
∴∠EDB=30°,
即∠EDB=∠B,
∴DE=EB,
∵BC=CE+BE,
∴BC=AC+DE,
∴BC=AC+AD.
2.(1)证明:在△ABC与△DCB中,
,
∴△ABC≌△DCB(SSS);
∴∠A=∠D;
(2)由(1)知∠A=∠D,
在△AOB与△DOC中,
,
∴△AOB≌△DOC(AAS),
∴OB=OC,
∵OC=2,
∴OB=OC=2.
3.证明:(1)∵∠ABC=45°,CD⊥AB于D,
∴△BCD是等腰直角三角形,H是BC边的中点,
∴BD=CD,
∵CD⊥AB于D,BE⊥AC于E,
∴∠DBF+∠A=90°,∠ACD+∠A=90°,
∴∠DBF=∠ACD,
在△BDF与△CDA中,
,
∴△BDF≌△CDA(ASA),
∴BF=AC;
(2)∵BE平分∠ABC,且BE⊥AC于E,
∴∠ABE=∠CBE,∠AEB=∠CEB=90°,
∴在△ABE与△CBE中,
,
∴△ABE≌△CBE(ASA),
∴AE=CE=AC,
∴BF=2CE,
即CE=BF;
(3)提出问题是连接DE,则∠DEB=45°,
证明如下:
∵∠CEB=∠CDB=90°,∴C,B,D,E四点共圆,
∴∠DEB=∠CDB=45°,
4.解:∵∠BCE=∠ACD=90°,
∴∠3+∠4=∠4+∠5,
∴∠3=∠5,
在△ABC和△DEC中,,
∴△ABC≌△DEC(AAS),
∴AC=CD;
(2)∵∠ACD=90°,AC=CD,
∴∠2=∠D=45°,
∵∠ACB=30°,∠BCE=∠ACD=90°,
∴∠4=60°,
∴∠AEC=180°﹣45°﹣60°=75°.
5.证明:∵DF是∠ADC的平分线,
∴∠CDF=∠ADF.
又∵AD=DC,DF=DF,
在△ADF与△CDF中,
,
∴△ADF≌△CDF,
∴AF=CF,
∴∠ACF=∠CAF.
∵AF∥CB,
∴∠CAF=∠ACB,
∴∠ACF=∠ACB,即CA平分∠BCF
6.证明:(1)∵BC∥DE,
∴∠ACB=∠CED,
在△ABC与△DCE中
,
∴△ABC≌△DCE(SAS),
∴AB=CD;
(2)∵△ABC≌△DCE,
∴∠A=∠D,∠ABC=∠DCE=75°,
∵∠ACB=65°,
∴∠A=∠D=180°﹣75°﹣65°=40°,
∴∠FBC=∠A+∠ACB=40°+65°=105°,
∵BC∥DE,
∴∠DFB=∠FBC=105°,
∴∠FGC=∠D+∠DFB=40°+105°=145°.
7.(1)证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE.
又∵∠A=∠D,∠B=∠C,
在△ABF与△DCE中,
,
∴△ABF≌△DCE(AAS),
∴AB=DC.
(2)△OEF为等腰三角形
理由如下:∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF,
∴△OEF为等腰三角形.
8.证明:在△ABC和△DCB中,
,
∴△ABC≌△DCB(SSS).
∴∠ABC=∠DCB.
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS).
∴AE=DE.
9.(1)证明:∵∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE,
(2)解:如图1中,设AC交BD于H.
∵△BAD≌△CAE,
∴∠HCO=∠HBA,
∵∠BHA=∠CHO,
∴∠COH=∠HAB=90°.
(3)如图2中,易证△BAD≌△CAE,
∴∠HCO=∠HBA,
∵∠BHA=∠CHO,
∴∠COH=∠HAB=60°.
(4)同法可证△BAD≌△CAE,
∴∠HCO=∠HBA,
∵∠BHA=∠CHO,
∴∠COH=∠HAB=x°.
故答案为x°.
10.解:(1)连接OC,在AM上截取AQ=CN,连接OQ,
∵O为CA、CB的垂直平分线的交点,
∴OC=OA=OB,
∵AC=BC,∴OC⊥AB,CO平分∠ACB,
∴∠A=∠B=45°,即∠ACB=90°,
∴∠OCN=45°,即∠OCN=∠A=45°,
在△AOQ和△CON中,
,
∴△AOQ≌△CON(SAS),
∴OQ=ON,∠AOQ=∠CON,
∵OC⊥AB,
∴∠AOC=∠AOQ+∠COQ=90°,
∴∠CON+∠COQ=90°,即∠QON=90°,
又∠MON=45°,
∴∠QOM=45°,
在△QOM和△NOM中,
∴△QOM≌△NOM(SAS),
∴QM=NM,
则AM=AQ+QM=CN+MN;
(2)MN=AM+CN.
11.解:∵AD⊥BC,BE⊥AC(已知),
∴∠ADB=∠ADC=∠BEC=90°(垂直定义),
又∵∠AFE=∠BFD(对顶角相等),
∴△AEF∽△BDF(两对对应角相等的两三角形相似),
∴∠FAE=∠FBD(相似三角形的对应角相等),
在△BFD和△ACD中,
,
∴△BFD≌△ACD(AAS),
∴BD=AD(全等三角形的对应边相等),
∴∠BAD=∠ABD(等边对等角),
又∵∠ADB=90°(已证),
∴∠ABC==45°(三角形的内角和定理).
12.解:(1)证明:由(x+AF)?a=(b﹣x+b﹣AF)?a,
得AF=b﹣x,
又EC=b﹣x,
∴AF=EC.
(2)翻折后的图形如图,
①如图1,当直线EE′经过原矩形顶点D时,x:b=,
如图2,当直线E′E经过原矩形的顶点A时,x:b=;
②如图1,当矩形E′E经过原矩形顶点D时,BE′∥EF,
理由如下:根据题意得,BE=DF,EE′=EF,
又∵∠BEE′=∠DEC=∠EDF,
∴在△BEE′与△FDE中,
,
∴△BEE′≌△FED(SAS),
∴∠BE′E=∠FED,
∴BE′∥EF;
如图2,当直线E′E经过原矩形的顶点A时,且当a:b=时,BE′与EF垂直.
13.解:(1)△ABP≌△ACQ,△ABQ≌△BCP
证明△ABP≌△ACQ
∵△ABC是等边三角形
∴∠BAP=∠ACQ=∠ABQ,AB=AC=BC
∵在△ABP和△ACQ中
∴△ABP≌△ACQ
(SAS)
(2)∵△ABP≌△ACQ
∴∠ABP=∠CAQ,∠BAQ+∠CAQ=60°
∴∠BAQ+∠ABP=60°
∵∠BOQ=∠BAQ+ABP
∴∠BOQ=60°.
(3)
如图所示,过点B作BD⊥AQ交AQ于点D
由(1)知△ABQ≌△BCP(SAS)
∴∠BAD=∠OBC
∴在△ABD和△BCO中
∴△ABD≌△BCO
(AAS)
∴AD=BO
在Rt△BOD中,∠BOD=60°,∠OBD=30°
∴BO=2OD
∴AD=2OD
∴点O为AD的中点
∴=
∴=.
14.证明:(1)如图1所示:
∵AD是∠BAC的角平分线,
∴∠BAD=∠CAD,
又∵EB⊥AB,
∴∠ABE=90°,
∴∠BAE+∠E=90°,
又∵∠CAD+∠ADC=90°,
∴∠ADC=∠E,
又∵∠ADC=∠BDE,
∴∠BDE=∠E,
∴BD=BE;
(2)过点D作DH⊥AB于H,设CF=5x,如图2所示:
∵∠ACB=90°,∴CD⊥AC,
又∵DH⊥AB,AD是∠BAC的角平分线,
∴CD=DH,
又∵EF⊥BD∴∠BFE=90°,
∴∠FEB+∠FBE=90°,
又∵∠ABC+∠FBE=90,
∴∠HBD=∠FEB,
∵DH⊥AB,∴∠BHD=90°,
∴∠BFE=∠BHD=90°,
在△BHD和△EBF中,
∴,
∴△BHD≌△EBF(AAS),
∴DH=BF,
∴CD=BF
∵CF:BF=5:3
∵CF=5x,∴BF=3x,CD=3x,
∴DF=CF﹣CD=5x﹣3x=2x,
∴BD=BF+DF=3x+2x═5x,
∵BE=10,
∴5x=10,x=2,
∴DF=4.
15.解:作出全等图形得(1分)
(1)BC=AB+AD…(2分)
(2)BC=BD+AD
证明:方法一:
在BC上截取BE=AB,连接DE,在BC上截取BF=BD,连接DF…(3分)
∵BD平分∠ABC,∴∠ABD=∠CBD
在△ABD和△EBD中
AB=BE
∠ABD=∠CBD
BD=BD
∴△ABD≌△EBD,
∴AD=DE…(4分)
∠DEB=∠A=100°
∴∠DEC=80°,
∵∠A=100°,∠C=40°
∴∠ABC=40°
∵BD平分∠ABC,
∴∠ABD=∠CBD=20°
∵BD=BF,
∴∠BFD=80°
∠DEC=∠BFD=80°,
∴DE=DF…(5分)
∵∠DFB=80°,∠C=40°
∴∠CDF=40°,
∴DF=CF
∴AD=CF
∴BC=BF+CF=BD+AD…(7分)
方法二:延长BD到F,使DF=AD,在BC上
截取BE=AB,通过证△ABE≌△DBE和
△CDF≌△CDE得到AD=DF;再证明BC=BF.
