人教版八年级上册数学分类(解答题)专练:12.2全等三角形判定(Word版 含答案)
文档属性
| 名称 | 人教版八年级上册数学分类(解答题)专练:12.2全等三角形判定(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 229.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-29 16:37:26 | ||
图片预览


文档简介
分类(解答题)专练:12.2全等三角形判定
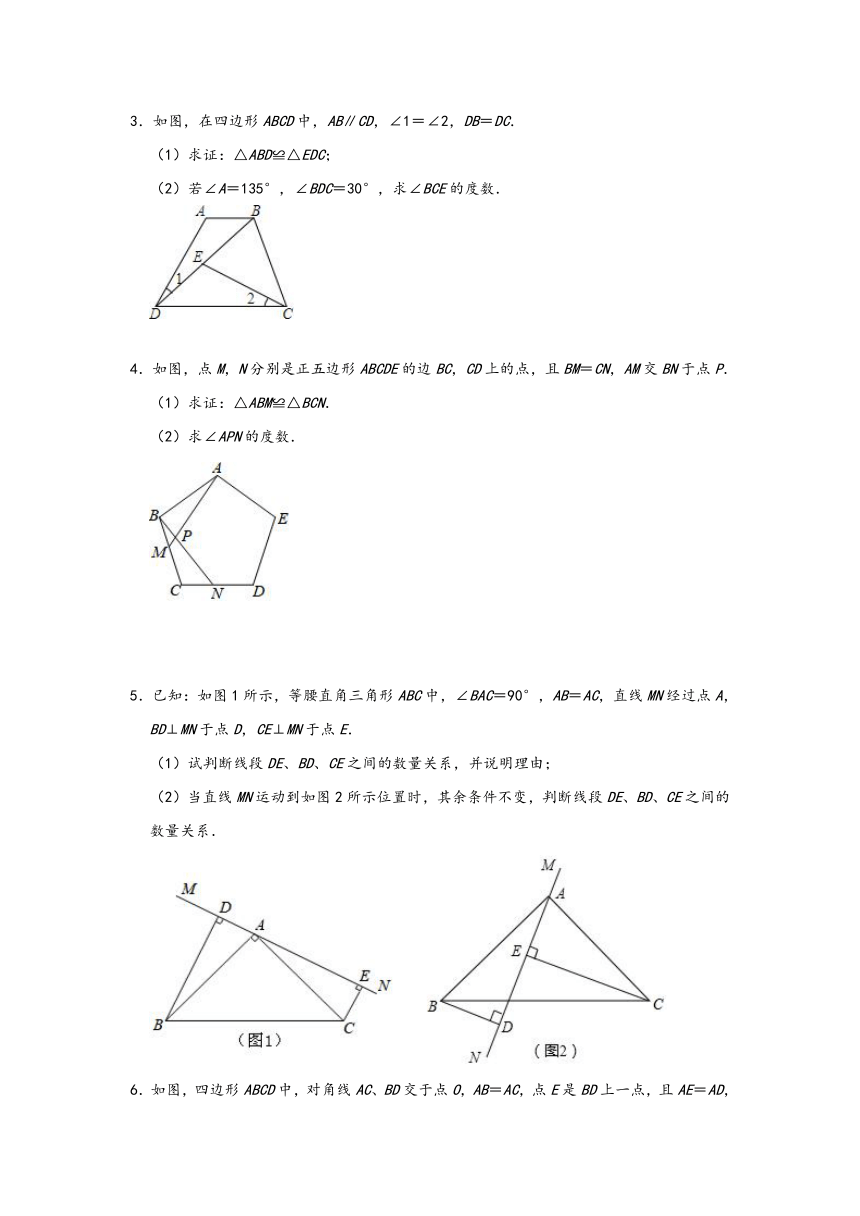
1.阅读探索题:
(1)如图1,OP是∠MON的平分线,以O为圆心任意长为半径作弧,分别交射线ON、OM于C、B两点,在射线OP上任取一点A(点O除外),连接AB、AC.求证:△AOB≌△AOC.
(2)请你参考以上方法,解答下列问题:
如图2,在
Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系并证明.
2.如图,在△ABC中,D为BC的中点,过D点的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF,并交AB于点E,连接EG,EF.
(1)求证:BG=CF.
(2)请你猜想BE+CF与EF的大小关系,并说明理由.
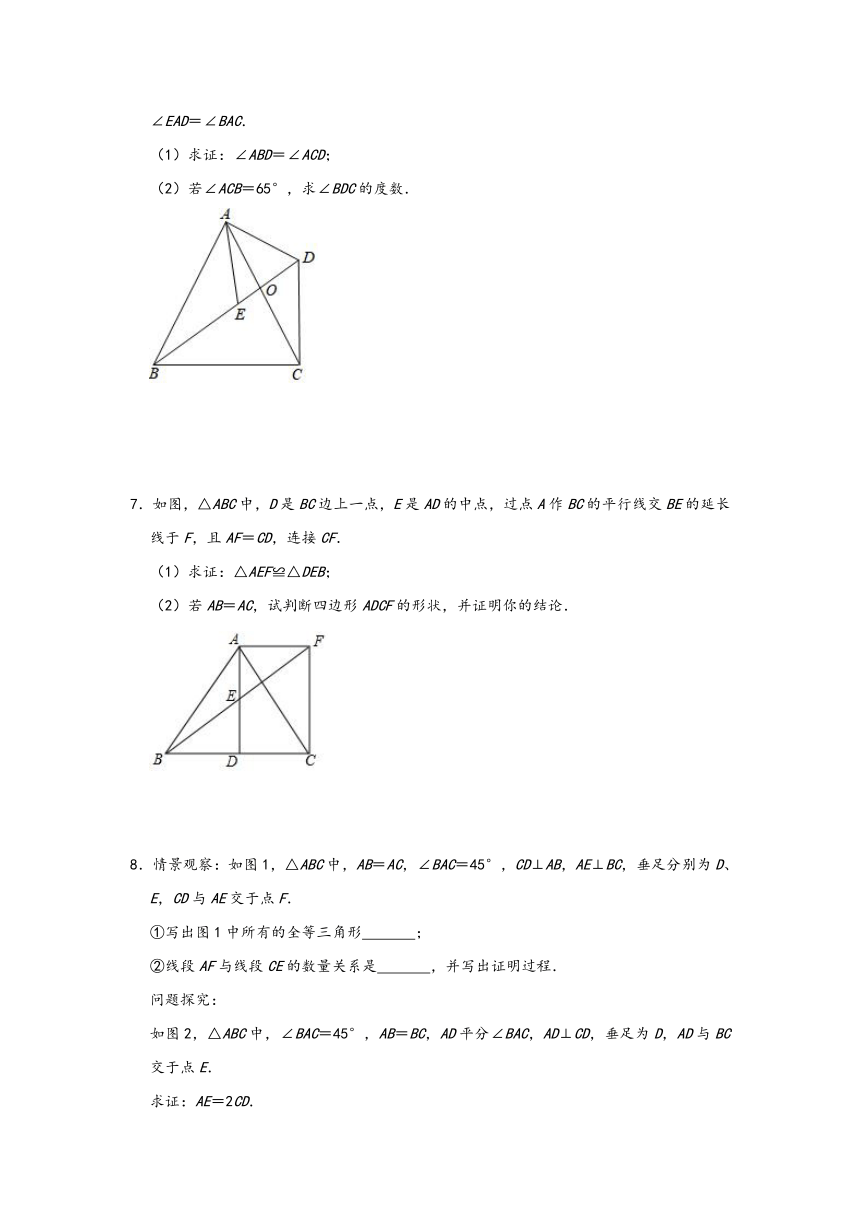
3.如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.
4.如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN.
(2)求∠APN的度数.
5.已知:如图1所示,等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.
(1)试判断线段DE、BD、CE之间的数量关系,并说明理由;
(2)当直线MN运动到如图2所示位置时,其余条件不变,判断线段DE、BD、CE之间的数量关系.
6.如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
(1)求证:∠ABD=∠ACD;
(2)若∠ACB=65°,求∠BDC的度数.
7.如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
8.情景观察:如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形
;
②线段AF与线段CE的数量关系是
,并写出证明过程.
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
9.如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
10.如图,已知△ABC中,AB=6cm,∠B=∠C,BC=4cm,点D为AB的中点.若点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
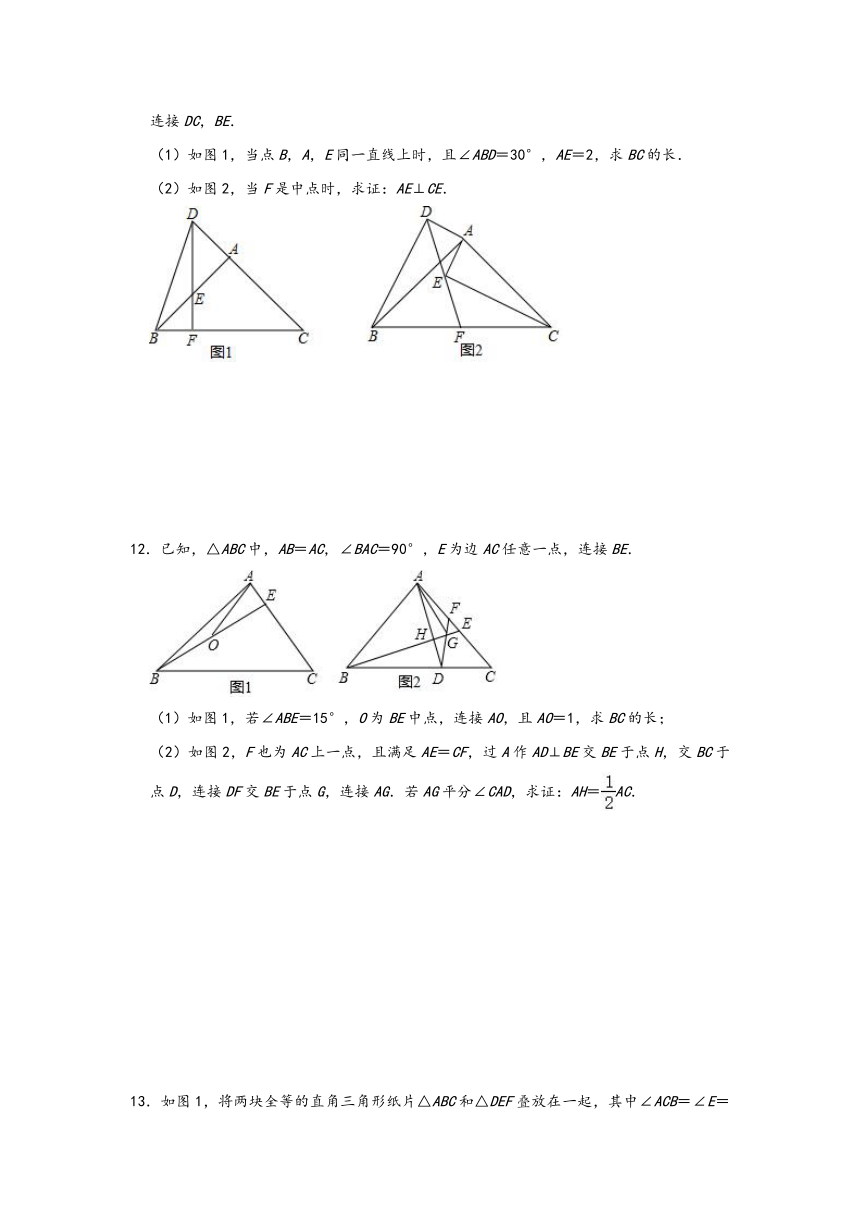
11.在△ABC与△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,延长DE交BC于点F,连接DC,BE.
(1)如图1,当点B,A,E同一直线上时,且∠ABD=30°,AE=2,求BC的长.
(2)如图2,当F是中点时,求证:AE⊥CE.
12.已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.
(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;
(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG.若AG平分∠CAD,求证:AH=AC.
13.如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;
(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
14.如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC.
(1)求∠APO+∠DCO的度数;
(2)求证:AC=AO+AP.
15.如图,已知:点D是△ABC的边BC上一动点,且AB=AC,DA=DE,∠BAC=∠ADE=α.
(1)如图1,当α=60°时,∠BCE=
;
(2)如图2,当α=90°时,试判断∠BCE的度数是否发生改变?若变化,请指出其变化范围;若不变化,请求出其值,并给出证明;
(3)如图3,当α=120°时,则∠BCE=
.
16.如图,CD是经过∠BCA顶点C的一条直线,且直线CD经过∠BCA的内部,点E,F在射线CD上,已知CA=CB且∠BEC=∠CFA=∠α.
(1)如图1,若∠BCA=90°,∠α=90°,问EF=BE﹣AF,成立吗?说明理由.
(2)将(1)中的已知条件改成∠BCA=60°,∠α=120°(如图2),问EF=BE﹣AF仍成立吗?说明理由.
(3)若0°<∠BCA<90°,请你添加一个关于∠α与∠BCA关系的条件,使结论EF=BE﹣AF仍然成立.你添加的条件是
.(直接写出结论)
参考答案
1.(1)证明:在△AOB和△AOC中,,
∴△AOB≌△AOC(SAS).
(2)在CB上截取CE=CA,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
在△ACD和△ECD中,,
∴△ACD≌△ECD(SAS),
∴∠CAD=∠CED=60°,
∵∠ACB=90°,
∴∠B=30°,
∴∠EDB=30°,
即∠EDB=∠B,
∴DE=EB,
∵BC=CE+BE,
∴BC=AC+DE,
∴BC=AC+AD.
2.(1)证明:∵BG∥AC,
∴∠C=∠GBD,
∵D是BC的中点,
∴BD=DC,
在△CFD和△BGD中
,
∴△CFD≌△BGD,
∴BG=CF.
(2)BE+CF>EF,
理由如下:
∵△CFD≌△BGD,
∴CF=BG,
在△BGE中,BG+BE>EG,
∵△CFD≌△BGD,
∴GD=DF,ED⊥GF,
∴EF=EG,
∴BG+CF>EF.
3.(1)证明:
∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(ASA),
(2)解:∵∠ABD=∠EDC=30°,∠A=135°,
∴∠1=∠2=15°,
∵DB=DC,
∴∠DCB==75°,
∴∠BCE=75°﹣15°=60°.
4.证明:(1)∵正五边形ABCDE,
∴AB=BC,∠ABM=∠C,
∴在△ABM和△BCN中
,
∴△ABM≌△BCN(SAS);
(2)∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC==108°.
即∠APN的度数为108°
5.解:(1)DE=BD+CE,理由如下:
∵BD⊥MN,CE⊥MN,
∴∠BDA=∠AEC=90°,
∴∠BAD+∠ABD=90°,
又∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE,
在△BAD和△ACE中
∴△BAD≌△ACE(AAS),
∴BD=AE,AD=CE,
又DE=AE+AD,
∴DE=BD+CE;
(2)DE=CE﹣BD,
同(1)可得△BAD≌△ACE,
故BD=AE,AD=CE,
又DE=AD﹣AE,
∴DE=CE﹣BD.
6.证明:(1)∵∠BAC=∠EAD
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC
即:∠BAE=∠CAD
在△ABE和△ACD中
∴△ABE≌△ACD
∴∠ABD=∠ACD
(2)∵∠BOC是△ABO和△DCO的外角
∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC
∴∠ABD+∠BAC=∠ACD+∠BDC
∵∠ABD=∠ACD
∴∠BAC=∠BDC
∵∠ACB=65°,AB=AC
∴∠ABC=∠ACB=65°
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=50°
∴∠BDC=∠BAC=50°.
7.证明:(1)∵E是AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,∠EAF=∠EDB,
∴△AEF≌△DEB(AAS);
(2)连接DF,
∵AF∥CD,AF=CD,
∴四边形ADCF是平行四边形,
∵△AEF≌△DEB,
∴BE=FE,
∵AE=DE,
∴四边形ABDF是平行四边形,
∴DF=AB,
∵AB=AC,
∴DF=AC,
∴四边形ADCF是矩形.
8.解:①图1中所有的全等三角形为△ABE≌△ACE,△ADF≌△CDB;
故答案为:△ABE≌△ACE,△ADF≌△CDB
②线段AF与线段CE的数量关系是:AF=2CE;
故答案为:AF=2CE.
证明:线段AF与线段CE的数量关系是AF=2CE,
∵△BCD≌△FAD,
∴AF=BC,
∵AB=AC,AE⊥BC,
∴BC=2CE,
∴AF=2CE;
问题探究:
证明:延长AB、CD交于点G,如图2所示:
∵AD平分∠BAC,
∴∠CAD=∠GAD,
∵AD⊥CD,
∴∠ADC=∠ADG=90°,
在△ADC和△ADG中,
,
∴△ADC≌△ADG(ASA),
∴CD=GD,即CG=2CD,
∵∠BAC=45°,AB=BC,
∴∠ABC=90°,
∴∠CBG=90°,
∴∠G+∠BCG=90°,
∵∠G+∠BAE=90°,
∴∠BAE=∠BCG,
在△ABE和△CBG中,
,
∴△ABE≌△CBG中(ASA),
∴AE=CG=2CD.
故答案为:①△ABE≌△ACE,△ADF≌△CDB;②AF=2CE;
9.(1)证明:∵CB=CA,DB=DA,
∴CD垂直平分线段AB,
∴CD⊥AB.
(2)①证明:∵AC=BC,
∴∠CBA=∠CAB,
又∵∠ACB=90°,
∴∠CBA=∠CAB=45°,
又∵∠CAD=∠CBD=15°,
∴∠DBA=∠DAB=30°,
∴∠BDE=30°+30°=60°,
∵AC=BC,∠CAD=∠CBD=15°,
∴BD=AD,
在△ADC和△BDC中,
,
∴△ADC≌△BDC(SAS),
∴∠ACD=∠BCD=45°,
∴∠CDE=60°,
∵∠CDE=∠BDE=60°,
∴DE平分∠BDC;
②解:结论:ME=BD,
理由:连接MC,
∵DC=DM,∠CDE=60°,
∴△MCD为等边三角形,
∴CM=CD,
∵EC=CA,∠EMC=120°,
∴∠ECM=∠BCD=45°
在△BDC和△EMC中,
,
∴△BDC≌△EMC(SAS),
∴ME=BD.
③当EN=EC时,∠ENC=7.5°或82.5°;当EN=CN时,∠ENC=150°;当CE=CN时,∠CNE=15°,
所以∠CNE的度数为7.5°、15°、82.5°、150°.
10.解:(1)全等,理由如下:
∵t=1秒,
∴BP=CQ=1×1=1厘米,
∵AB=6cm,点D为AB的中点,
∴BD=3cm.
又∵PC=BC﹣BP,BC=4cm,
∴PC=4﹣1=3cm,
∴PC=BD.
∵∠B=∠C,
∴△BPD≌△CPQ;
(2)∵vP≠vQ,
∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,
则BP=CP=2,BD=CQ=3,
∴点P,点Q运动的时间为:t=2秒,
∴vQ=1.5cm/s;
11.略
12.(1)略
(2)证明:如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.
∵BE⊥AP,
∴∠AHB=90°,
∴∠ABH+∠BAH=90°,
∵∠BAH+∠PAC=90°,
∴∠ABE=∠PAC,
在△ABE和△CAP中,
,
∴△ABE≌△CAP,
∴AE=CP=CF,∠AEB=∠P,
在△DCF和△DCP中,
,
∴△DCF≌△DCP,
∴∠DFC=∠P,
∴∠GFE=∠GEF,
∴GE=GF,∵GM⊥EF,
∴FM=ME,
∵AE=CF,
∴AF=CE,
∴AM=CM,
在△GAH和△GAM中,
,
∴△AGH≌△AGM,
∴AH=AM=CM=AC.
13.解:(1)∵∠ACB=90°,D是AB的中点,
∴DC=DB=DA.
∴∠B=∠DCB.
又∵△ABC≌△FDE,
∴∠FDE=∠B.
∴∠FDE=∠DCB.
∴DG∥BC.
∴∠AGD=∠ACB=90°.
∴DG⊥AC.
又∵DC=DA,
∴G是AC的中点.
∴CG=AC=×8=4,DG=BC=×6=3.
∴S△DCG=×CG?DG=×4×3=6.
(2)略
14.解:(1)连接BO,如图1所示:
∵AB=AC,AD⊥BC,
∴BD=CD,∠ODB=∠ODC,
在△OBD和△OCD中,
,
∴△OBD≌△OCD(SAS),
∴OB=OC,
又∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DBO=∠DCO,
又∵∠BAC=120°,
∠ABC=∠ACB=30°,
又∵∠ABD=∠ABO+∠DBO=30°,
∴APO+∠DCO=30°;
(2)过点O作OH⊥BP于点H,如图2所示:
∵∠BAC=120°,AB=AC,AD⊥BC,
∴∠HAO=∠CAD=60°,
又∵OH⊥BP,
∴∠OHA=90°,
∴∠HOA=30°,
∴AO=2AH,
又∵BO=PO,OH⊥BP,
∴BH=PH,
又∵HP=AP+AH,
∴BH=AP+AH,
又∵AB=BH+AH,
∴AB=AP+2AH,
又∵AB=AC,AO=2AH,
∴AC=AP+AO.
15.解:(1)如图,且AB=AC,DA=DE,∠BAC=∠ADE=60°
∴△ABC和△ADE是等边三角形,
∴∠BAD+∠DAC=∠EAC+∠DAC=60°,AD=AE,∠BCA=60°,
即,∠BAD=∠CAE,
∴△BAD≌△CAE,
∴∠B=∠ACE=60°,
∴∠BCE=∠BCA+∠ACE=120°;
(2)如图,
过D作DF⊥BC,交CA延长线于F,
∵∠BAC=∠FDC=90°,
∴∠ACB=∠DFC=45°,
∴在直角△FDC中:DF=DC,
又∵∠FDA+∠ADC=∠CDE+∠ADC=90°,
∴∠FDA=∠CDE
又∵DA=DE,
∴△FDA≌△CDE,
∴∠DFA=∠BCE,
∴∠BCE=45°;
同理,过D作DF⊥BC,AC于点F时,∠DFA=∠BCE=135°.
综上所述,∠BCE=45°或∠BCE=135°;
(3)如图,
作∠FDC=120°,交CA的延长线于F.
∵∠ADE=∠BAC=120°,
∴∠FDA+∠ADC=∠CDE+∠ADC,∠ACB=30°,
∴∠FDA=∠CDE,∠DFC=∠ACB=30°,DF=DC,
又∵AD=DE,
∴△FDA≌△CDE,
∴∠DCE=∠DFA=30°.
当点E在直线BC上方时,同法可得∠BCE=120°,
综上所述,∠BCE=30°或120°.
16.解:(1)EF=BE﹣AF成立,理由为:
在△BCE中,∠BEC=90°,∴∠CBE+∠BCE=90°,
∵∠BCA=90°,∴∠ACF+∠BCE=90°,
∴∠CBE=∠ACF,
又BC=CA,∠BEC=∠CFA=90°,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
又∵EF=CF﹣CE,
∴EF=BE﹣AF;
(2)EF=BE﹣AF仍成立,理由为:
在△BCE中,∠BEC=120°,∴∠CBE+∠BCE=60°,
∵∠BCA=60°,∴∠ACF+∠BCE=60°,
∴∠CBE=∠ACF,
又BC=CA,∠BEC=∠CFA=120°,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
又∵EF=CF﹣CE,
∴EF=BE﹣AF;
(3)当∠α+∠BCA=180°时,结论EF=BE﹣AF仍然成立.
故答案为:∠α+∠BCA=180°.
1.阅读探索题:
(1)如图1,OP是∠MON的平分线,以O为圆心任意长为半径作弧,分别交射线ON、OM于C、B两点,在射线OP上任取一点A(点O除外),连接AB、AC.求证:△AOB≌△AOC.
(2)请你参考以上方法,解答下列问题:
如图2,在
Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系并证明.
2.如图,在△ABC中,D为BC的中点,过D点的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF,并交AB于点E,连接EG,EF.
(1)求证:BG=CF.
(2)请你猜想BE+CF与EF的大小关系,并说明理由.
3.如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.
4.如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN.
(2)求∠APN的度数.
5.已知:如图1所示,等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.
(1)试判断线段DE、BD、CE之间的数量关系,并说明理由;
(2)当直线MN运动到如图2所示位置时,其余条件不变,判断线段DE、BD、CE之间的数量关系.
6.如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
(1)求证:∠ABD=∠ACD;
(2)若∠ACB=65°,求∠BDC的度数.
7.如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
8.情景观察:如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形
;
②线段AF与线段CE的数量关系是
,并写出证明过程.
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
9.如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
10.如图,已知△ABC中,AB=6cm,∠B=∠C,BC=4cm,点D为AB的中点.若点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
11.在△ABC与△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,延长DE交BC于点F,连接DC,BE.
(1)如图1,当点B,A,E同一直线上时,且∠ABD=30°,AE=2,求BC的长.
(2)如图2,当F是中点时,求证:AE⊥CE.
12.已知,△ABC中,AB=AC,∠BAC=90°,E为边AC任意一点,连接BE.
(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;
(2)如图2,F也为AC上一点,且满足AE=CF,过A作AD⊥BE交BE于点H,交BC于点D,连接DF交BE于点G,连接AG.若AG平分∠CAD,求证:AH=AC.
13.如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;
(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
14.如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC.
(1)求∠APO+∠DCO的度数;
(2)求证:AC=AO+AP.
15.如图,已知:点D是△ABC的边BC上一动点,且AB=AC,DA=DE,∠BAC=∠ADE=α.
(1)如图1,当α=60°时,∠BCE=
;
(2)如图2,当α=90°时,试判断∠BCE的度数是否发生改变?若变化,请指出其变化范围;若不变化,请求出其值,并给出证明;
(3)如图3,当α=120°时,则∠BCE=
.
16.如图,CD是经过∠BCA顶点C的一条直线,且直线CD经过∠BCA的内部,点E,F在射线CD上,已知CA=CB且∠BEC=∠CFA=∠α.
(1)如图1,若∠BCA=90°,∠α=90°,问EF=BE﹣AF,成立吗?说明理由.
(2)将(1)中的已知条件改成∠BCA=60°,∠α=120°(如图2),问EF=BE﹣AF仍成立吗?说明理由.
(3)若0°<∠BCA<90°,请你添加一个关于∠α与∠BCA关系的条件,使结论EF=BE﹣AF仍然成立.你添加的条件是
.(直接写出结论)
参考答案
1.(1)证明:在△AOB和△AOC中,,
∴△AOB≌△AOC(SAS).
(2)在CB上截取CE=CA,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
在△ACD和△ECD中,,
∴△ACD≌△ECD(SAS),
∴∠CAD=∠CED=60°,
∵∠ACB=90°,
∴∠B=30°,
∴∠EDB=30°,
即∠EDB=∠B,
∴DE=EB,
∵BC=CE+BE,
∴BC=AC+DE,
∴BC=AC+AD.
2.(1)证明:∵BG∥AC,
∴∠C=∠GBD,
∵D是BC的中点,
∴BD=DC,
在△CFD和△BGD中
,
∴△CFD≌△BGD,
∴BG=CF.
(2)BE+CF>EF,
理由如下:
∵△CFD≌△BGD,
∴CF=BG,
在△BGE中,BG+BE>EG,
∵△CFD≌△BGD,
∴GD=DF,ED⊥GF,
∴EF=EG,
∴BG+CF>EF.
3.(1)证明:
∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(ASA),
(2)解:∵∠ABD=∠EDC=30°,∠A=135°,
∴∠1=∠2=15°,
∵DB=DC,
∴∠DCB==75°,
∴∠BCE=75°﹣15°=60°.
4.证明:(1)∵正五边形ABCDE,
∴AB=BC,∠ABM=∠C,
∴在△ABM和△BCN中
,
∴△ABM≌△BCN(SAS);
(2)∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∵∠BAM+∠ABP=∠APN,
∴∠CBN+∠ABP=∠APN=∠ABC==108°.
即∠APN的度数为108°
5.解:(1)DE=BD+CE,理由如下:
∵BD⊥MN,CE⊥MN,
∴∠BDA=∠AEC=90°,
∴∠BAD+∠ABD=90°,
又∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE,
在△BAD和△ACE中
∴△BAD≌△ACE(AAS),
∴BD=AE,AD=CE,
又DE=AE+AD,
∴DE=BD+CE;
(2)DE=CE﹣BD,
同(1)可得△BAD≌△ACE,
故BD=AE,AD=CE,
又DE=AD﹣AE,
∴DE=CE﹣BD.
6.证明:(1)∵∠BAC=∠EAD
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC
即:∠BAE=∠CAD
在△ABE和△ACD中
∴△ABE≌△ACD
∴∠ABD=∠ACD
(2)∵∠BOC是△ABO和△DCO的外角
∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC
∴∠ABD+∠BAC=∠ACD+∠BDC
∵∠ABD=∠ACD
∴∠BAC=∠BDC
∵∠ACB=65°,AB=AC
∴∠ABC=∠ACB=65°
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=50°
∴∠BDC=∠BAC=50°.
7.证明:(1)∵E是AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,∠EAF=∠EDB,
∴△AEF≌△DEB(AAS);
(2)连接DF,
∵AF∥CD,AF=CD,
∴四边形ADCF是平行四边形,
∵△AEF≌△DEB,
∴BE=FE,
∵AE=DE,
∴四边形ABDF是平行四边形,
∴DF=AB,
∵AB=AC,
∴DF=AC,
∴四边形ADCF是矩形.
8.解:①图1中所有的全等三角形为△ABE≌△ACE,△ADF≌△CDB;
故答案为:△ABE≌△ACE,△ADF≌△CDB
②线段AF与线段CE的数量关系是:AF=2CE;
故答案为:AF=2CE.
证明:线段AF与线段CE的数量关系是AF=2CE,
∵△BCD≌△FAD,
∴AF=BC,
∵AB=AC,AE⊥BC,
∴BC=2CE,
∴AF=2CE;
问题探究:
证明:延长AB、CD交于点G,如图2所示:
∵AD平分∠BAC,
∴∠CAD=∠GAD,
∵AD⊥CD,
∴∠ADC=∠ADG=90°,
在△ADC和△ADG中,
,
∴△ADC≌△ADG(ASA),
∴CD=GD,即CG=2CD,
∵∠BAC=45°,AB=BC,
∴∠ABC=90°,
∴∠CBG=90°,
∴∠G+∠BCG=90°,
∵∠G+∠BAE=90°,
∴∠BAE=∠BCG,
在△ABE和△CBG中,
,
∴△ABE≌△CBG中(ASA),
∴AE=CG=2CD.
故答案为:①△ABE≌△ACE,△ADF≌△CDB;②AF=2CE;
9.(1)证明:∵CB=CA,DB=DA,
∴CD垂直平分线段AB,
∴CD⊥AB.
(2)①证明:∵AC=BC,
∴∠CBA=∠CAB,
又∵∠ACB=90°,
∴∠CBA=∠CAB=45°,
又∵∠CAD=∠CBD=15°,
∴∠DBA=∠DAB=30°,
∴∠BDE=30°+30°=60°,
∵AC=BC,∠CAD=∠CBD=15°,
∴BD=AD,
在△ADC和△BDC中,
,
∴△ADC≌△BDC(SAS),
∴∠ACD=∠BCD=45°,
∴∠CDE=60°,
∵∠CDE=∠BDE=60°,
∴DE平分∠BDC;
②解:结论:ME=BD,
理由:连接MC,
∵DC=DM,∠CDE=60°,
∴△MCD为等边三角形,
∴CM=CD,
∵EC=CA,∠EMC=120°,
∴∠ECM=∠BCD=45°
在△BDC和△EMC中,
,
∴△BDC≌△EMC(SAS),
∴ME=BD.
③当EN=EC时,∠ENC=7.5°或82.5°;当EN=CN时,∠ENC=150°;当CE=CN时,∠CNE=15°,
所以∠CNE的度数为7.5°、15°、82.5°、150°.
10.解:(1)全等,理由如下:
∵t=1秒,
∴BP=CQ=1×1=1厘米,
∵AB=6cm,点D为AB的中点,
∴BD=3cm.
又∵PC=BC﹣BP,BC=4cm,
∴PC=4﹣1=3cm,
∴PC=BD.
∵∠B=∠C,
∴△BPD≌△CPQ;
(2)∵vP≠vQ,
∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,
则BP=CP=2,BD=CQ=3,
∴点P,点Q运动的时间为:t=2秒,
∴vQ=1.5cm/s;
11.略
12.(1)略
(2)证明:如图2中,作CP⊥AC,交AD的延长线于P,GM⊥AC于M.
∵BE⊥AP,
∴∠AHB=90°,
∴∠ABH+∠BAH=90°,
∵∠BAH+∠PAC=90°,
∴∠ABE=∠PAC,
在△ABE和△CAP中,
,
∴△ABE≌△CAP,
∴AE=CP=CF,∠AEB=∠P,
在△DCF和△DCP中,
,
∴△DCF≌△DCP,
∴∠DFC=∠P,
∴∠GFE=∠GEF,
∴GE=GF,∵GM⊥EF,
∴FM=ME,
∵AE=CF,
∴AF=CE,
∴AM=CM,
在△GAH和△GAM中,
,
∴△AGH≌△AGM,
∴AH=AM=CM=AC.
13.解:(1)∵∠ACB=90°,D是AB的中点,
∴DC=DB=DA.
∴∠B=∠DCB.
又∵△ABC≌△FDE,
∴∠FDE=∠B.
∴∠FDE=∠DCB.
∴DG∥BC.
∴∠AGD=∠ACB=90°.
∴DG⊥AC.
又∵DC=DA,
∴G是AC的中点.
∴CG=AC=×8=4,DG=BC=×6=3.
∴S△DCG=×CG?DG=×4×3=6.
(2)略
14.解:(1)连接BO,如图1所示:
∵AB=AC,AD⊥BC,
∴BD=CD,∠ODB=∠ODC,
在△OBD和△OCD中,
,
∴△OBD≌△OCD(SAS),
∴OB=OC,
又∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DBO=∠DCO,
又∵∠BAC=120°,
∠ABC=∠ACB=30°,
又∵∠ABD=∠ABO+∠DBO=30°,
∴APO+∠DCO=30°;
(2)过点O作OH⊥BP于点H,如图2所示:
∵∠BAC=120°,AB=AC,AD⊥BC,
∴∠HAO=∠CAD=60°,
又∵OH⊥BP,
∴∠OHA=90°,
∴∠HOA=30°,
∴AO=2AH,
又∵BO=PO,OH⊥BP,
∴BH=PH,
又∵HP=AP+AH,
∴BH=AP+AH,
又∵AB=BH+AH,
∴AB=AP+2AH,
又∵AB=AC,AO=2AH,
∴AC=AP+AO.
15.解:(1)如图,且AB=AC,DA=DE,∠BAC=∠ADE=60°
∴△ABC和△ADE是等边三角形,
∴∠BAD+∠DAC=∠EAC+∠DAC=60°,AD=AE,∠BCA=60°,
即,∠BAD=∠CAE,
∴△BAD≌△CAE,
∴∠B=∠ACE=60°,
∴∠BCE=∠BCA+∠ACE=120°;
(2)如图,
过D作DF⊥BC,交CA延长线于F,
∵∠BAC=∠FDC=90°,
∴∠ACB=∠DFC=45°,
∴在直角△FDC中:DF=DC,
又∵∠FDA+∠ADC=∠CDE+∠ADC=90°,
∴∠FDA=∠CDE
又∵DA=DE,
∴△FDA≌△CDE,
∴∠DFA=∠BCE,
∴∠BCE=45°;
同理,过D作DF⊥BC,AC于点F时,∠DFA=∠BCE=135°.
综上所述,∠BCE=45°或∠BCE=135°;
(3)如图,
作∠FDC=120°,交CA的延长线于F.
∵∠ADE=∠BAC=120°,
∴∠FDA+∠ADC=∠CDE+∠ADC,∠ACB=30°,
∴∠FDA=∠CDE,∠DFC=∠ACB=30°,DF=DC,
又∵AD=DE,
∴△FDA≌△CDE,
∴∠DCE=∠DFA=30°.
当点E在直线BC上方时,同法可得∠BCE=120°,
综上所述,∠BCE=30°或120°.
16.解:(1)EF=BE﹣AF成立,理由为:
在△BCE中,∠BEC=90°,∴∠CBE+∠BCE=90°,
∵∠BCA=90°,∴∠ACF+∠BCE=90°,
∴∠CBE=∠ACF,
又BC=CA,∠BEC=∠CFA=90°,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
又∵EF=CF﹣CE,
∴EF=BE﹣AF;
(2)EF=BE﹣AF仍成立,理由为:
在△BCE中,∠BEC=120°,∴∠CBE+∠BCE=60°,
∵∠BCA=60°,∴∠ACF+∠BCE=60°,
∴∠CBE=∠ACF,
又BC=CA,∠BEC=∠CFA=120°,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
又∵EF=CF﹣CE,
∴EF=BE﹣AF;
(3)当∠α+∠BCA=180°时,结论EF=BE﹣AF仍然成立.
故答案为:∠α+∠BCA=180°.
