苏科版七年级数学第二章有理数复习教案
图片预览


文档简介
??
姓名:
年级:
初一
学科:
日期:
教学目标
1.理解有理数及其运算的意义,发展运算能力;了解无理数的概念,会判断无理数.
2.能用数轴上的点表示有理数,会比较有理数的大小;借助数轴理解相反数和绝对值的意义,会求有理数的相反数与绝对值.
3.体会转化、归纳等思想;掌握有理数的加、减、乘、除、乘方及混合运算并能解决简单的实际问题.4.会用科学记数法表示较大的数,能对含有较大数字的信息作出合理的解释和推断,发展数感.
教学重点
能用数轴上的点表示有理数,会比较有理数的大小;借助数轴理解相反数和绝对值的意义,会求有理数的相反数与绝对值.
教学难点
体会转化、归纳等思想;掌握有理数的加、减、乘、除、乘方及混合运算并能解决简单的实际问题.
教学内容
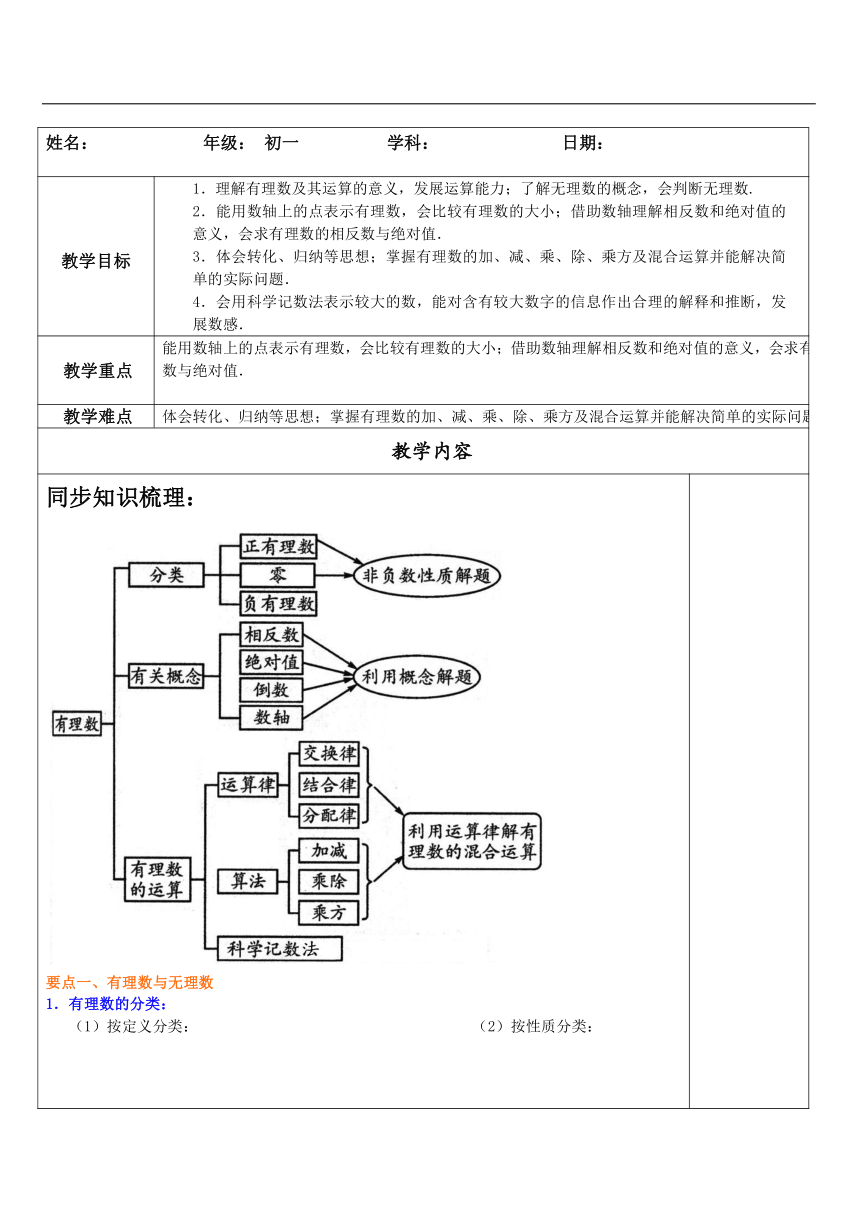
同步知识梳理:要点一、有理数与无理数1.有理数的分类:
(1)按定义分类:
(2)按性质分类:要点诠释:(1)用正数、负数表示相反意义的量;(2)有理数“0”的作用:作用举例表示数的性质0是自然数、是有理数表示没有3个苹果用+3表示,没有苹果用0表示表示某种状态
表示冰点表示正数与负数的界点0非正非负,是一个中性数2.无理数:无限不循环小数叫做无理数.要点诠释:(1)无理数的特征:无理数的小数部分位数无限.无理数的小数部分不循环,不能表示成分数的形式.
(2)目前常见的无理数有两种形式:①含类.②看似循环而实质不循环的数,
如:1.313113111……(相邻两个3之间1的个数逐渐增加).
3.数轴:规定了原点、正方向和单位长度的直线.要点诠释:(1)一切有理数都可以用数轴上的点表示出来,数轴上的点不都表示的是有理数,如.(2)在数轴上,右边的点所对应的数总比左边的点所对应的数大.4.相反数:只有符号不同的两个数互称为相反数,0的相反数是0.
要点诠释:(1)一对相反数在数轴上对应的点位于原点两侧,并且到原点的距离相等,这两点是关于原点对称的.(2)求任意一个数的相反数,只要在这个数的前面添上“”号即可.(3)多重符号的化简:数字前面“”号的个数若有偶数个时,化简结果为正,若有奇数个时,化简结果为负.5.绝对值:(1)代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
数a的绝对值记作.
(2)几何意义:一个数a的绝对值就是数轴上表示数a的点与原点的距离.要点二、有理数的运算
1
.法则:(1)加法法则:①同号两数相加,取相同的符号,并把绝对值相加.②绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.③一个数同0相加,仍得这个数.(2)减法法则:减去一个数,等于加这个数的相反数.即a-b=a+(-b)
.(3)乘法法则:①两数相乘,同号得正,异号得负,并把绝对值相乘.②任何数同0相乘,都得0.(4)除法法则:除以一个不等于0的数,等于乘这个数的倒数.即a÷b=a·(b≠0)
.
(5)乘方运算的符号法则:①负数的奇次幂是负数,负数的偶次幂是正数;②正数的任何次幂都是正数,0的任何非零次幂都是0.
(6)有理数的混合运算顺序:①先乘方,再乘除,最后加减;②同级运算,从左到右进行;③如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.要点诠释:“奇负偶正”口诀的应用:(1)多重负号的化简,这里奇偶指的是“-”号的个数,例如:-[-(-3)]=-3,-[+(-3)]=3.(2)有理数乘法,当多个非零因数相乘时,这里奇偶指的是负因数的个数,正负指结果中积的符号,例如:(-3)×(-2)×(-6)=-36,而(-3)×(-2)×6=36.(3)有理数乘方,这里奇偶指的是指数,当底数为负数时,指数为奇数,则幂为负;指数为偶数,则幂为正,例如:
,
.2.运算律:
(1)交换律:
①加法交换律:a+b=b+a;
②乘法交换律:ab=ba;(2)结合律:
①加法结合律:(a+b)+c=a+(b+c);
②乘法结合律:(ab)c=a(bc)
(3)分配律:a(b+c)=ab+ac要点三、有理数的大小比较比较大小常用的方法有:(1)数轴比较法;(2)法则比较法:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小;(3)
作差比较法.(4)作商比较法;(5)倒数比较法.要点四、科学记数法
把一个大于10的数表示成的形式(其中,是正整数),此种记法叫做科学记数法.例如:200
000=.例题精讲:类型一、有理数与无理数的相关概念
1.已知x与y互为相反数,m与n互为倒数,|x+y
|+(a-1)2=0,求a2-(x+y+mn)a+(x+y)2009+(-mn)2010的值.2.(2016?江西校级模拟)如果m,n互为相反数,那么|m+n﹣2016|=________.类型二、有理数的运算3.(1)
(2)
4.先观察下列各式:;;;…;,根据以上观察,计算:…的值.类型三、数学思想在本章中的应用5.(1)阅读下面材料:点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|.当A,B两点中有一点在原点时,不妨设点A在原点,如图(1),|AB|=|OB|=|b|=|a﹣b|;当A,B两点都不在原点时,①如图(2),点A,B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;②如图(3),点A,B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;③如图(4),点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=|a﹣b|;综上,数轴上A,B两点之间的距离|AB|=|a﹣b|.(2)回答下列问题:①数轴上表示2和5的两点之间的距离是
,数轴上表示﹣2和﹣5的两点之间的距离是
,数轴上表示1和﹣3的两点之间的距离是
;②数轴上表示x和﹣1的两点A和B之间的距离是
,如果|AB|=2,那么x为
;③当代数式|x+1|+|x﹣2|取最小值时,相应的x的取值范围是
.④解方程|x+1|+|x﹣2|=5.世界上著名的莱布尼茨三角形如图所示,则排在第10行从左边数第3个位置上的数是(
)A.
B.
C.
D.课堂练习:1.已知四种说法:
①|a|=a时,a>0;
|a|=-a时,
a<0.
②|a|就是a与-a中较大的数.
③|a|就是数轴上a到原点的距离.
④对于任意有理数,-|a|≤a≤|a|.
其中说法正确的个数是(
)
A.1
B.2
C.3
D.4
2.有四个说法:
①有最小的有理数
②有绝对值最小的有理数
③有最小的正有理数
④没有最大的负有理数
上述说法正确的是(
)
A.①②
B.③④
C.②④
D.①②
3.已知(-ab)3>0,则(
)
A.ab<0
B.ab>0
C.a>0且b<0
D.a<0且b<0
4.若|x-1|+|y+3|+|z-5|=0,则(x+1)(y-3)(z+5)的值是(
)
A.120
B.-15
C.0
D.-120
5.下列各对算式中,结果相等的是(
)
A.-a6与(-a)6
B.-a3与|-a|3
C.[(-a)2]3与(-a3)2
D.(ab)3与ab3
6.下列实数中是无理数的是( )A.
B.3.143
C.
D.3.101001000…(0的个数逐渐增加)7.在“百度”搜索引擎中输入“姚明”,能搜索到与之相关的网页约27000000个,将这个数用科学记数法表示为( )
A.2.7×105
B.
2.7×106
C.
2.7×107
D.
2.7×1088.计算:(1)(2)
课后作业:1.
与比较大小,必定为(
).A.
B.
C.
D.这要取决于b2.下列语句中,正确的个数是(
).①一个数与它的相反数的商为-1;②两个有理数之和大于其中任意一个加数;③若两数之和为正数,则这两个数一定都是正数;④若,则.
A.0
B.1
C.2
D.303.记,令,称为,,…,这列数的“理想数”.已知,,…,的“理想数”为2004,那么8,,,…,的“理想数”为(
)
A.2004
B.2006
C.2008
D.20104.甲、乙两队合做修一条1200米的路,甲队独做4小时可以完成,乙队独做6小时可以完成,问两人合做2小时能修多少米?( )
A.600米
B.
800
C.
1000米
D.
1200米5.把下列各数填在相应的表示集合的大括号内:-3,-0.4,π,-|-4|,-,0,4.262262226…(两个6之间依次增加一个“2”).整??数{????????????????????????????…}
负分数{?????????????????????????????…}
无理数{?????????????????????????????…}.6.如图,有理数对应数轴上两点A,B,判断下列各式的符号:________0;________0;0;________0.7.已知满足,则代数式的值是
。
课后作业
PAGE
姓名:
年级:
初一
学科:
日期:
教学目标
1.理解有理数及其运算的意义,发展运算能力;了解无理数的概念,会判断无理数.
2.能用数轴上的点表示有理数,会比较有理数的大小;借助数轴理解相反数和绝对值的意义,会求有理数的相反数与绝对值.
3.体会转化、归纳等思想;掌握有理数的加、减、乘、除、乘方及混合运算并能解决简单的实际问题.4.会用科学记数法表示较大的数,能对含有较大数字的信息作出合理的解释和推断,发展数感.
教学重点
能用数轴上的点表示有理数,会比较有理数的大小;借助数轴理解相反数和绝对值的意义,会求有理数的相反数与绝对值.
教学难点
体会转化、归纳等思想;掌握有理数的加、减、乘、除、乘方及混合运算并能解决简单的实际问题.
教学内容
同步知识梳理:要点一、有理数与无理数1.有理数的分类:
(1)按定义分类:
(2)按性质分类:要点诠释:(1)用正数、负数表示相反意义的量;(2)有理数“0”的作用:作用举例表示数的性质0是自然数、是有理数表示没有3个苹果用+3表示,没有苹果用0表示表示某种状态
表示冰点表示正数与负数的界点0非正非负,是一个中性数2.无理数:无限不循环小数叫做无理数.要点诠释:(1)无理数的特征:无理数的小数部分位数无限.无理数的小数部分不循环,不能表示成分数的形式.
(2)目前常见的无理数有两种形式:①含类.②看似循环而实质不循环的数,
如:1.313113111……(相邻两个3之间1的个数逐渐增加).
3.数轴:规定了原点、正方向和单位长度的直线.要点诠释:(1)一切有理数都可以用数轴上的点表示出来,数轴上的点不都表示的是有理数,如.(2)在数轴上,右边的点所对应的数总比左边的点所对应的数大.4.相反数:只有符号不同的两个数互称为相反数,0的相反数是0.
要点诠释:(1)一对相反数在数轴上对应的点位于原点两侧,并且到原点的距离相等,这两点是关于原点对称的.(2)求任意一个数的相反数,只要在这个数的前面添上“”号即可.(3)多重符号的化简:数字前面“”号的个数若有偶数个时,化简结果为正,若有奇数个时,化简结果为负.5.绝对值:(1)代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
数a的绝对值记作.
(2)几何意义:一个数a的绝对值就是数轴上表示数a的点与原点的距离.要点二、有理数的运算
1
.法则:(1)加法法则:①同号两数相加,取相同的符号,并把绝对值相加.②绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.③一个数同0相加,仍得这个数.(2)减法法则:减去一个数,等于加这个数的相反数.即a-b=a+(-b)
.(3)乘法法则:①两数相乘,同号得正,异号得负,并把绝对值相乘.②任何数同0相乘,都得0.(4)除法法则:除以一个不等于0的数,等于乘这个数的倒数.即a÷b=a·(b≠0)
.
(5)乘方运算的符号法则:①负数的奇次幂是负数,负数的偶次幂是正数;②正数的任何次幂都是正数,0的任何非零次幂都是0.
(6)有理数的混合运算顺序:①先乘方,再乘除,最后加减;②同级运算,从左到右进行;③如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.要点诠释:“奇负偶正”口诀的应用:(1)多重负号的化简,这里奇偶指的是“-”号的个数,例如:-[-(-3)]=-3,-[+(-3)]=3.(2)有理数乘法,当多个非零因数相乘时,这里奇偶指的是负因数的个数,正负指结果中积的符号,例如:(-3)×(-2)×(-6)=-36,而(-3)×(-2)×6=36.(3)有理数乘方,这里奇偶指的是指数,当底数为负数时,指数为奇数,则幂为负;指数为偶数,则幂为正,例如:
,
.2.运算律:
(1)交换律:
①加法交换律:a+b=b+a;
②乘法交换律:ab=ba;(2)结合律:
①加法结合律:(a+b)+c=a+(b+c);
②乘法结合律:(ab)c=a(bc)
(3)分配律:a(b+c)=ab+ac要点三、有理数的大小比较比较大小常用的方法有:(1)数轴比较法;(2)法则比较法:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小;(3)
作差比较法.(4)作商比较法;(5)倒数比较法.要点四、科学记数法
把一个大于10的数表示成的形式(其中,是正整数),此种记法叫做科学记数法.例如:200
000=.例题精讲:类型一、有理数与无理数的相关概念
1.已知x与y互为相反数,m与n互为倒数,|x+y
|+(a-1)2=0,求a2-(x+y+mn)a+(x+y)2009+(-mn)2010的值.2.(2016?江西校级模拟)如果m,n互为相反数,那么|m+n﹣2016|=________.类型二、有理数的运算3.(1)
(2)
4.先观察下列各式:;;;…;,根据以上观察,计算:…的值.类型三、数学思想在本章中的应用5.(1)阅读下面材料:点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|.当A,B两点中有一点在原点时,不妨设点A在原点,如图(1),|AB|=|OB|=|b|=|a﹣b|;当A,B两点都不在原点时,①如图(2),点A,B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;②如图(3),点A,B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;③如图(4),点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=|a﹣b|;综上,数轴上A,B两点之间的距离|AB|=|a﹣b|.(2)回答下列问题:①数轴上表示2和5的两点之间的距离是
,数轴上表示﹣2和﹣5的两点之间的距离是
,数轴上表示1和﹣3的两点之间的距离是
;②数轴上表示x和﹣1的两点A和B之间的距离是
,如果|AB|=2,那么x为
;③当代数式|x+1|+|x﹣2|取最小值时,相应的x的取值范围是
.④解方程|x+1|+|x﹣2|=5.世界上著名的莱布尼茨三角形如图所示,则排在第10行从左边数第3个位置上的数是(
)A.
B.
C.
D.课堂练习:1.已知四种说法:
①|a|=a时,a>0;
|a|=-a时,
a<0.
②|a|就是a与-a中较大的数.
③|a|就是数轴上a到原点的距离.
④对于任意有理数,-|a|≤a≤|a|.
其中说法正确的个数是(
)
A.1
B.2
C.3
D.4
2.有四个说法:
①有最小的有理数
②有绝对值最小的有理数
③有最小的正有理数
④没有最大的负有理数
上述说法正确的是(
)
A.①②
B.③④
C.②④
D.①②
3.已知(-ab)3>0,则(
)
A.ab<0
B.ab>0
C.a>0且b<0
D.a<0且b<0
4.若|x-1|+|y+3|+|z-5|=0,则(x+1)(y-3)(z+5)的值是(
)
A.120
B.-15
C.0
D.-120
5.下列各对算式中,结果相等的是(
)
A.-a6与(-a)6
B.-a3与|-a|3
C.[(-a)2]3与(-a3)2
D.(ab)3与ab3
6.下列实数中是无理数的是( )A.
B.3.143
C.
D.3.101001000…(0的个数逐渐增加)7.在“百度”搜索引擎中输入“姚明”,能搜索到与之相关的网页约27000000个,将这个数用科学记数法表示为( )
A.2.7×105
B.
2.7×106
C.
2.7×107
D.
2.7×1088.计算:(1)(2)
课后作业:1.
与比较大小,必定为(
).A.
B.
C.
D.这要取决于b2.下列语句中,正确的个数是(
).①一个数与它的相反数的商为-1;②两个有理数之和大于其中任意一个加数;③若两数之和为正数,则这两个数一定都是正数;④若,则.
A.0
B.1
C.2
D.303.记,令,称为,,…,这列数的“理想数”.已知,,…,的“理想数”为2004,那么8,,,…,的“理想数”为(
)
A.2004
B.2006
C.2008
D.20104.甲、乙两队合做修一条1200米的路,甲队独做4小时可以完成,乙队独做6小时可以完成,问两人合做2小时能修多少米?( )
A.600米
B.
800
C.
1000米
D.
1200米5.把下列各数填在相应的表示集合的大括号内:-3,-0.4,π,-|-4|,-,0,4.262262226…(两个6之间依次增加一个“2”).整??数{????????????????????????????…}
负分数{?????????????????????????????…}
无理数{?????????????????????????????…}.6.如图,有理数对应数轴上两点A,B,判断下列各式的符号:________0;________0;0;________0.7.已知满足,则代数式的值是
。
课后作业
PAGE
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
