人教版数学九年级下册28.1 锐角三角函数 课时3课件(32张)
文档属性
| 名称 | 人教版数学九年级下册28.1 锐角三角函数 课时3课件(32张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 888.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览





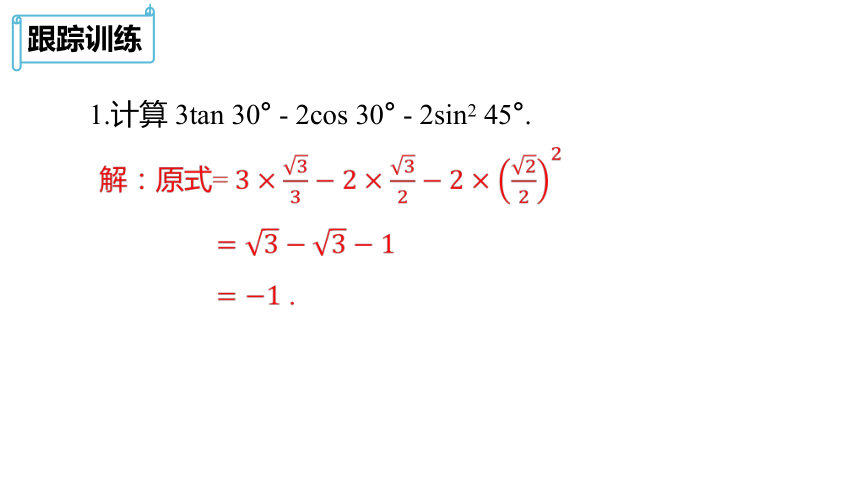
文档简介
28.1 锐角三角函数
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
A
B
C
∠A 的邻边
∠A 的对边
斜边
∠A的邻边
斜边
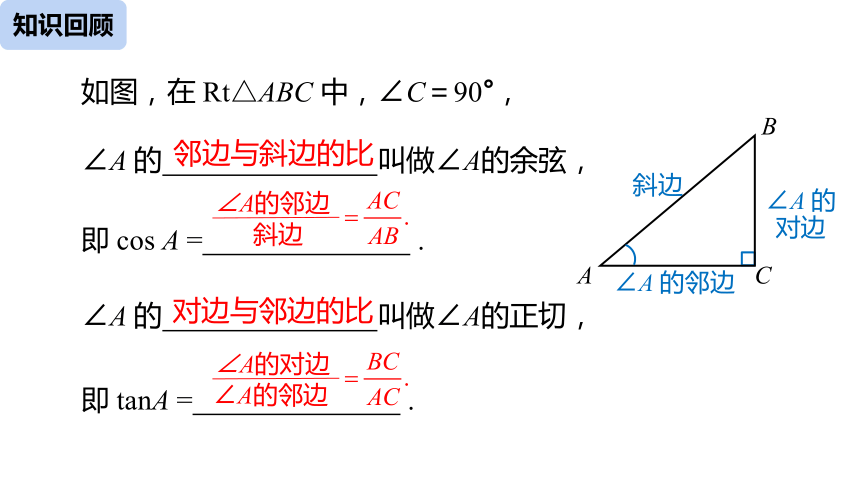
如图,在 Rt△ABC 中,∠C=90°,
∠A 的 叫做∠A的余弦,
即 cos A = .
邻边与斜边的比
∠A 的 叫做∠A的正切,
即 tanA = .
∠A的对边
∠A的邻边
对边与邻边的比
学习目标
1.运用三角函数的知识,自主探索,推导出30°、45°、60°角的三角函数值.
2.熟记三个特殊锐角的三角函数值,并能准确地加以运用.
课堂导入
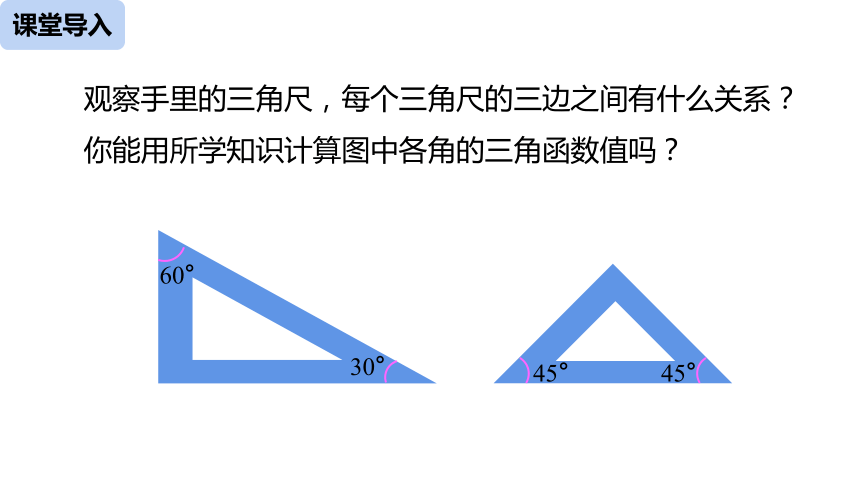
观察手里的三角尺,每个三角尺的三边之间有什么关系?你能用所学知识计算图中各角的三角函数值吗?
30°
60°
45°
45°
新知探究
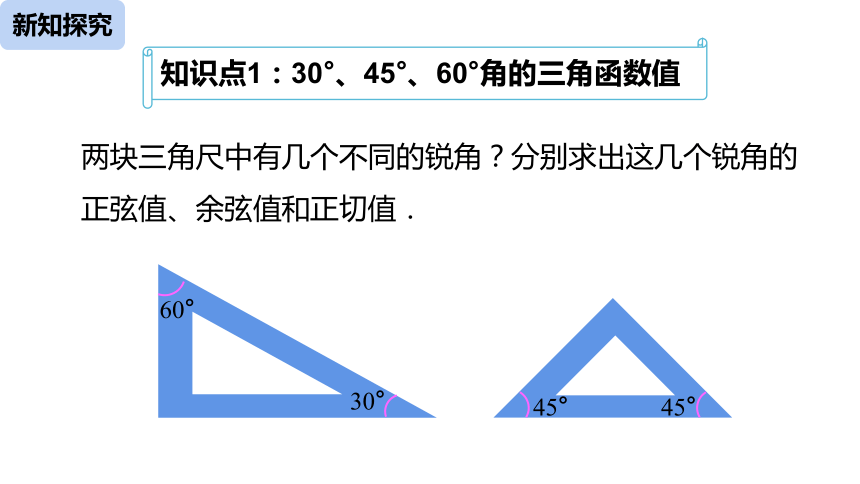
知识点1:30°、45°、60°角的三角函数值
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
60°
45°
45°
新知探究
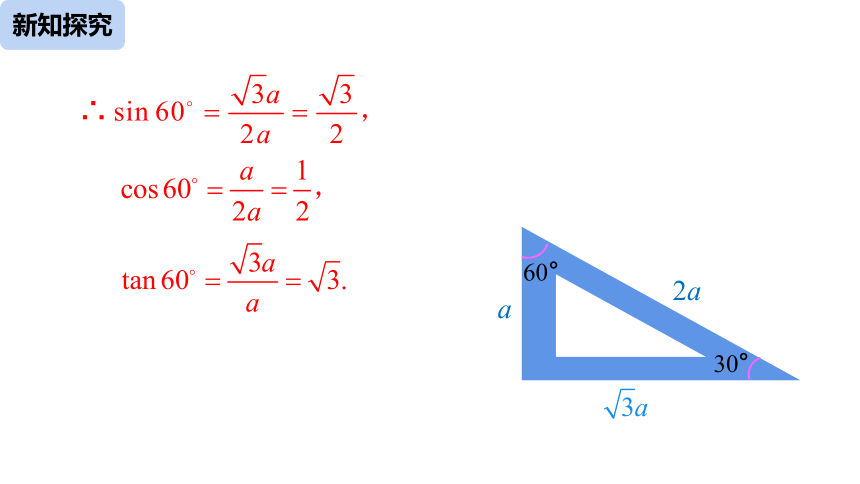
设 30°角所对的直角边长为 a,那么斜边长为 2a,
另一条直角边长 =
∴
a
2a
30°
60°
新知探究
∴
a
2a
30°
60°
新知探究
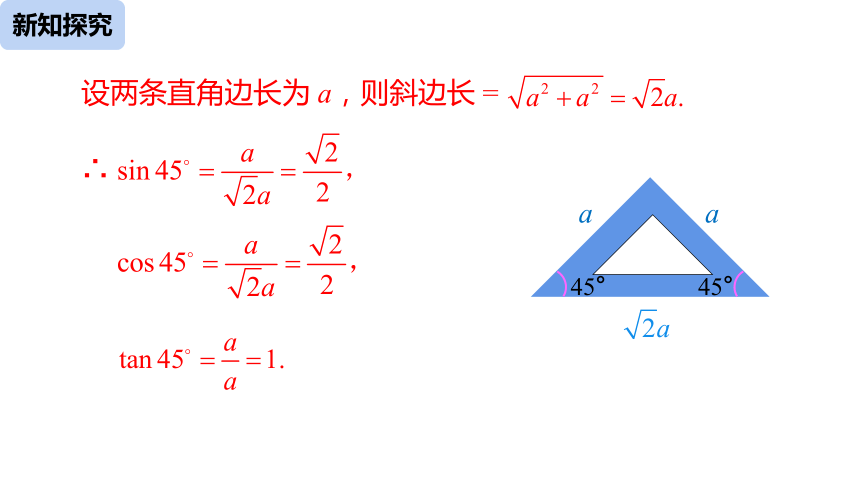
设两条直角边长为 a,则斜边长 =
∴
45°
45°
a
a
30°
45°
60°
sin α
cos α
tan α
新知探究
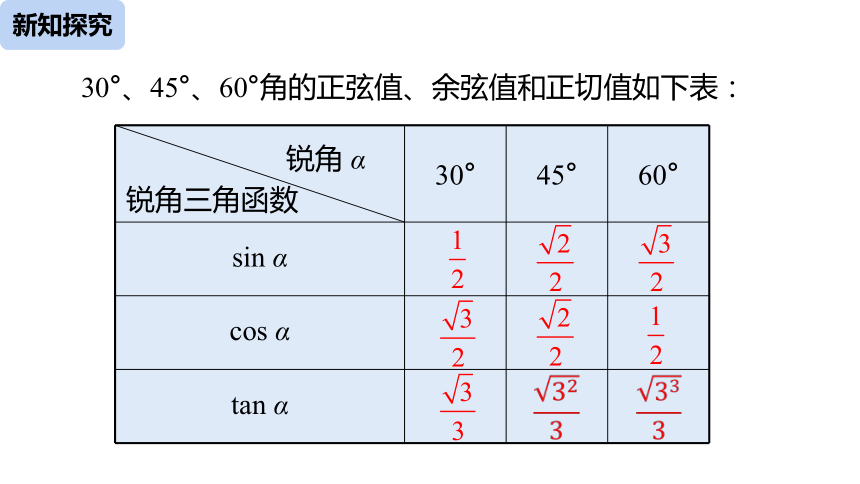
30°、45°、60°角的正弦值、余弦值和正切值如下表:
323
?
锐角三角函数
锐角 α
333
?
新知探究
记忆口诀
1,2,3;3,2,1;3,9,27;
弦比2,切比3,分子根号别忘添.
已知特殊角的度数,可求出相应的三角函数值;反之,已知一个特殊角的三角函数值,也可求出这个角的度数.
新知探究
例3 求下列各式的值:
解:cos260°+sin260°
(1) cos260°+sin260°;
cos260°表示(cos60°)2,
即 (cos60°)·(cos60°).
(2)
解:
跟踪训练
1.计算 3tan 30° - 2cos 30° - 2sin2 45°.
解:原式= 3×33?2×32?2×222
=3?3?1
=?1 .
?
跟踪训练
2.如图,已知⊙O 的两条弦AC,BD 相交于点E,∠BAC=70°,∠C=50°,那么sin∠AEB的值为( )
A. 12 B. 33
C. 22 D. 32
?
D
70°
70°
50°
60°
60°
新知探究
知识点2:通过三角函数值求角度
解: 在图中,
A
B
C
例4 (1) 如图,在 Rt△ABC中,∠C = 90°,AB = 6,BC = 3,求 ∠A 的度数;
?
∴ ∠A = 45°.
∵
新知探究
解: 在图中,
∴ α = 60°.
∵ tanα = ,
(2) 如图,AO 是圆锥的高,OB 是底面半径,AO = 3OB,求 α 的度数.
?
A
B
O
新知探究
已知 △ABC 中的∠A 与∠B 满足 (1-tanA)2 +|sinB - 32|=0,试判断 △ABC 的形状.
?
解:∵ (1-tanA)2 + | sinB- |=0,
∴ tanA-1=0,sinB- =0,
∴ tanA=1,sinB=
∴ ∠A=45°,∠B=60°,
∠C=180°-45°-60°=75°,
∴△ABC 是锐角三角形.
跟踪训练
1.在 Rt△ABC 中,∠C =90°,BC = 7 ,AC = 21 ,求∠A,∠B 的度数.
?
B
A
C
21
?
7
?
还有其他解法吗?
跟踪训练
1.在 Rt△ABC 中,∠C =90°,BC = 7 ,AC = 21 ,求∠A,∠B 的度数.
?
B
A
C
21
?
7
?
27
?
跟踪训练
1.在 Rt△ABC 中,∠C =90°,BC = 7 ,AC = 21 ,求∠A,∠B 的度数.
?
B
A
C
21
?
7
?
27
?
跟踪训练
2.如图,在△ABC 中,∠C=90°,点D 在AC 上.已知∠BDC=45°,BD=102,AB=20,求∠A 的度数.
?
解:在Rt△BDC中,
BC=BD·sin∠BDC=102×22=10,
在 Rt△ACB中,
∵ sinA=????????????????=1020=12,
∴∠A=30°.
?
随堂练习
1.sin60°的倒数为( )
A. 2 B. 32 C. 33 D. 233
?
????????
?
????????????
?
D
随堂练习
2.若△ABC 中,sin A=cos B=22,则下列最确切的结论是( )
A. △ABC 是直角三角形
B. △ABC 是等腰三角形
C. △ABC 是等腰直角三角形
D. △ABC 是锐角三角形
?
C
∠A=∠B=45°
随堂练习
3.已知α为锐角,且关于x的方程x2-tan α·x+14=0有两个相等的实根,则α 的度数为( )
A.30° B.45° C.60° D.90°
?
B
????=?tan?????2?4×14=0
?
tan?????=1
?
随堂练习
4.计算:
(1) ;
(2) ;
(3) .
解:(1)原式 ;
(2)原式 ;
(3)原式 .
随堂练习
随堂练习
5.在△ABC 中,∠A,∠B 满足 |sinA- 32| - ( 33-tan B)2=0,试判断△ABC 的形状,并说明理由.
?
sin????=32→∠A=60°
?
tan????=33→∠B=30°
?
随堂练习
5.在△ABC 中,∠A,∠B 满足 |sin A- 32| - ( 33-tan B)2=0,试判断△ABC 的形状,并说明理由.
?
解:∵ |sin A- 32| - ( 33-tan B)2=0 ,
?
∴ sin A-32=0,33-tan B=0 ,
∴ sin A= 32 ,tan B= 33 ,
∴ ∠A=60°,∠B=30°,
∠C=180°-60°-30°=90°,
∴△ABC 是直角三角形.
?
课堂小结
特殊角的三角函数值:
30°
45°
60°
sin α
cos α
tan α
1
锐角三角函数
锐角 α
对接中考
1.(2020·天津中考)2sin45°的值等于( )
A. 1
B. 2
C. 3
D. 2
?
2×22=2
?
B
对接中考
2.(2019·怀化中考)已知∠α为锐角,且sinα=12,则∠α=( )
A.30°
B.45°
C.60°
D.90°
?
sin30°=12
?
A
对接中考
3.(2019·甘肃中考)在△ABC 中,∠C =90°,tan A = 33 ,则 cos B =_______.
?
∠A =30°
∠B =60°
cos????=12
?
12
?
课后作业
请完成课本后习题第3题.
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
A
B
C
∠A 的邻边
∠A 的对边
斜边
∠A的邻边
斜边
如图,在 Rt△ABC 中,∠C=90°,
∠A 的 叫做∠A的余弦,
即 cos A = .
邻边与斜边的比
∠A 的 叫做∠A的正切,
即 tanA = .
∠A的对边
∠A的邻边
对边与邻边的比
学习目标
1.运用三角函数的知识,自主探索,推导出30°、45°、60°角的三角函数值.
2.熟记三个特殊锐角的三角函数值,并能准确地加以运用.
课堂导入
观察手里的三角尺,每个三角尺的三边之间有什么关系?你能用所学知识计算图中各角的三角函数值吗?
30°
60°
45°
45°
新知探究
知识点1:30°、45°、60°角的三角函数值
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
30°
60°
45°
45°
新知探究
设 30°角所对的直角边长为 a,那么斜边长为 2a,
另一条直角边长 =
∴
a
2a
30°
60°
新知探究
∴
a
2a
30°
60°
新知探究
设两条直角边长为 a,则斜边长 =
∴
45°
45°
a
a
30°
45°
60°
sin α
cos α
tan α
新知探究
30°、45°、60°角的正弦值、余弦值和正切值如下表:
323
?
锐角三角函数
锐角 α
333
?
新知探究
记忆口诀
1,2,3;3,2,1;3,9,27;
弦比2,切比3,分子根号别忘添.
已知特殊角的度数,可求出相应的三角函数值;反之,已知一个特殊角的三角函数值,也可求出这个角的度数.
新知探究
例3 求下列各式的值:
解:cos260°+sin260°
(1) cos260°+sin260°;
cos260°表示(cos60°)2,
即 (cos60°)·(cos60°).
(2)
解:
跟踪训练
1.计算 3tan 30° - 2cos 30° - 2sin2 45°.
解:原式= 3×33?2×32?2×222
=3?3?1
=?1 .
?
跟踪训练
2.如图,已知⊙O 的两条弦AC,BD 相交于点E,∠BAC=70°,∠C=50°,那么sin∠AEB的值为( )
A. 12 B. 33
C. 22 D. 32
?
D
70°
70°
50°
60°
60°
新知探究
知识点2:通过三角函数值求角度
解: 在图中,
A
B
C
例4 (1) 如图,在 Rt△ABC中,∠C = 90°,AB = 6,BC = 3,求 ∠A 的度数;
?
∴ ∠A = 45°.
∵
新知探究
解: 在图中,
∴ α = 60°.
∵ tanα = ,
(2) 如图,AO 是圆锥的高,OB 是底面半径,AO = 3OB,求 α 的度数.
?
A
B
O
新知探究
已知 △ABC 中的∠A 与∠B 满足 (1-tanA)2 +|sinB - 32|=0,试判断 △ABC 的形状.
?
解:∵ (1-tanA)2 + | sinB- |=0,
∴ tanA-1=0,sinB- =0,
∴ tanA=1,sinB=
∴ ∠A=45°,∠B=60°,
∠C=180°-45°-60°=75°,
∴△ABC 是锐角三角形.
跟踪训练
1.在 Rt△ABC 中,∠C =90°,BC = 7 ,AC = 21 ,求∠A,∠B 的度数.
?
B
A
C
21
?
7
?
还有其他解法吗?
跟踪训练
1.在 Rt△ABC 中,∠C =90°,BC = 7 ,AC = 21 ,求∠A,∠B 的度数.
?
B
A
C
21
?
7
?
27
?
跟踪训练
1.在 Rt△ABC 中,∠C =90°,BC = 7 ,AC = 21 ,求∠A,∠B 的度数.
?
B
A
C
21
?
7
?
27
?
跟踪训练
2.如图,在△ABC 中,∠C=90°,点D 在AC 上.已知∠BDC=45°,BD=102,AB=20,求∠A 的度数.
?
解:在Rt△BDC中,
BC=BD·sin∠BDC=102×22=10,
在 Rt△ACB中,
∵ sinA=????????????????=1020=12,
∴∠A=30°.
?
随堂练习
1.sin60°的倒数为( )
A. 2 B. 32 C. 33 D. 233
?
????????
?
????????????
?
D
随堂练习
2.若△ABC 中,sin A=cos B=22,则下列最确切的结论是( )
A. △ABC 是直角三角形
B. △ABC 是等腰三角形
C. △ABC 是等腰直角三角形
D. △ABC 是锐角三角形
?
C
∠A=∠B=45°
随堂练习
3.已知α为锐角,且关于x的方程x2-tan α·x+14=0有两个相等的实根,则α 的度数为( )
A.30° B.45° C.60° D.90°
?
B
????=?tan?????2?4×14=0
?
tan?????=1
?
随堂练习
4.计算:
(1) ;
(2) ;
(3) .
解:(1)原式 ;
(2)原式 ;
(3)原式 .
随堂练习
随堂练习
5.在△ABC 中,∠A,∠B 满足 |sinA- 32| - ( 33-tan B)2=0,试判断△ABC 的形状,并说明理由.
?
sin????=32→∠A=60°
?
tan????=33→∠B=30°
?
随堂练习
5.在△ABC 中,∠A,∠B 满足 |sin A- 32| - ( 33-tan B)2=0,试判断△ABC 的形状,并说明理由.
?
解:∵ |sin A- 32| - ( 33-tan B)2=0 ,
?
∴ sin A-32=0,33-tan B=0 ,
∴ sin A= 32 ,tan B= 33 ,
∴ ∠A=60°,∠B=30°,
∠C=180°-60°-30°=90°,
∴△ABC 是直角三角形.
?
课堂小结
特殊角的三角函数值:
30°
45°
60°
sin α
cos α
tan α
1
锐角三角函数
锐角 α
对接中考
1.(2020·天津中考)2sin45°的值等于( )
A. 1
B. 2
C. 3
D. 2
?
2×22=2
?
B
对接中考
2.(2019·怀化中考)已知∠α为锐角,且sinα=12,则∠α=( )
A.30°
B.45°
C.60°
D.90°
?
sin30°=12
?
A
对接中考
3.(2019·甘肃中考)在△ABC 中,∠C =90°,tan A = 33 ,则 cos B =_______.
?
∠A =30°
∠B =60°
cos????=12
?
12
?
课后作业
请完成课本后习题第3题.
