人教版数学九年级下册28.1 锐角三角函数 课时4课件(28张)
文档属性
| 名称 | 人教版数学九年级下册28.1 锐角三角函数 课时4课件(28张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览





文档简介
28.1 锐角三角函数
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
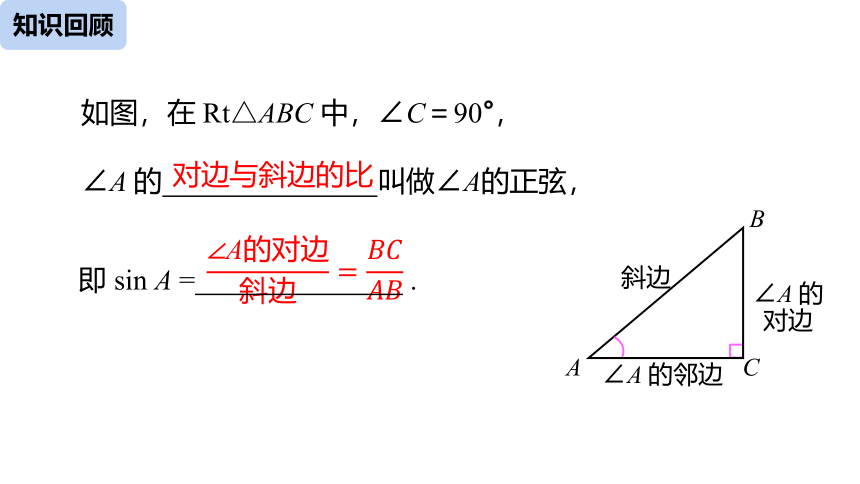
如图,在 Rt△ABC 中,∠C=90°,
∠A 的 叫做∠A的正弦,
对边与斜边的比
∠A的对边斜边=????????????????
?
即 sin A = .
A
B
C
∠A 的邻边
∠A 的
对边
斜边
知识回顾
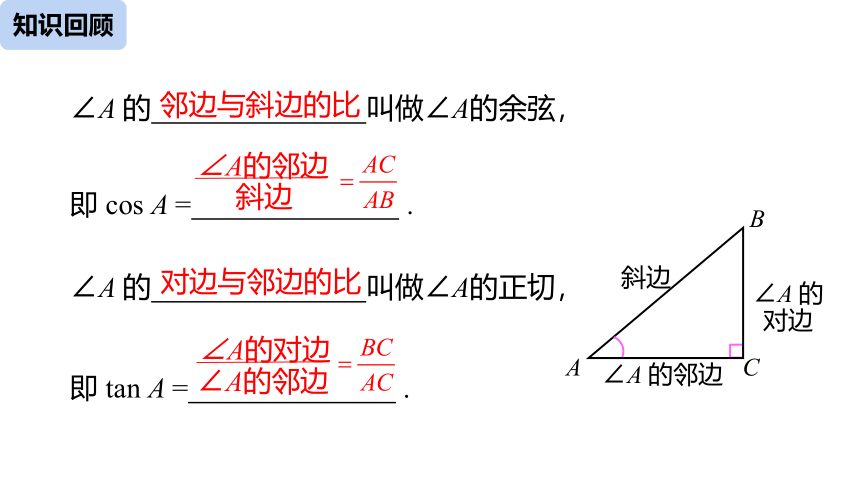
∠A的邻边
斜边
∠A 的 叫做∠A的余弦,
即 cos A = .
邻边与斜边的比
即 tan A = .
∠A的对边
∠A的邻边
对边与邻边的比
∠A 的 叫做∠A的正切,
A
B
C
∠A 的邻边
∠A 的
对边
斜边
学习目标
2.能根据锐角三角函数的定义解决与直角三角形有关的简单计算.
1.进一步认识锐角正弦、余弦和正切.
课堂导入
通过前面的学习,我们知道在直角三角形中,利用三角函数可以求出相关边长和角的度数,那么,在其他图形中我们能利用三角函数解决问题吗?
新知探究
知识点:利用三角函数解决问题
1.如图,在 Rt△ABC 中,∠C=90°,∠BAC=30°,延长 CA 至 D 点,使 AD=AB.
(1)求∠D;
(2)求tan D 的值.
D
A
C
B
解: (1) ∵ AB =AD,
∴ ∠D =∠ABD,
∵ ∠BAC =∠D +∠ABD =30°,
∴ ∠D =15°.
新知探究
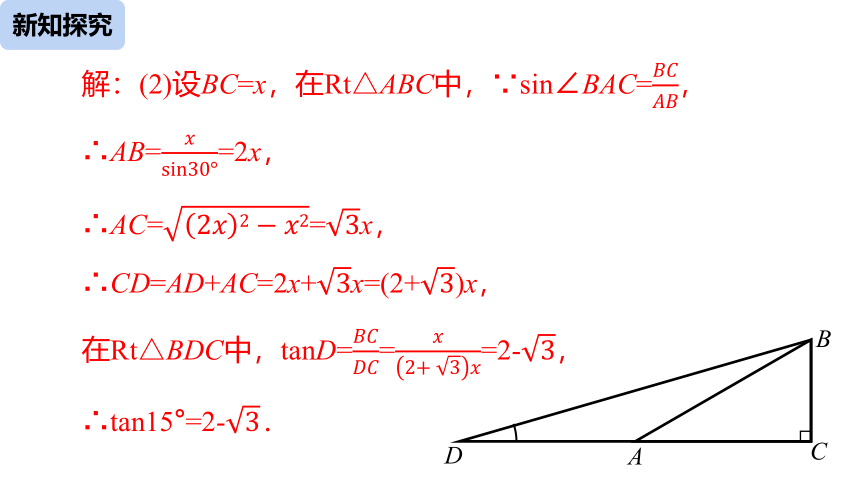
解:(2)设BC=x,在Rt△ABC中,∵sin∠BAC=????????????????,
∴AB=????sin30°=2x,
∴AC=2????2?????2=3x,
∴CD=AD+AC=2x+3x=(2+3)x,
在Rt△BDC中,tanD=????????????????=????2+3????=2-3,
∴tan15°=2-3.
?
D
A
C
B
新知探究
D
A
C
B
x
x
2x
?
2x
?
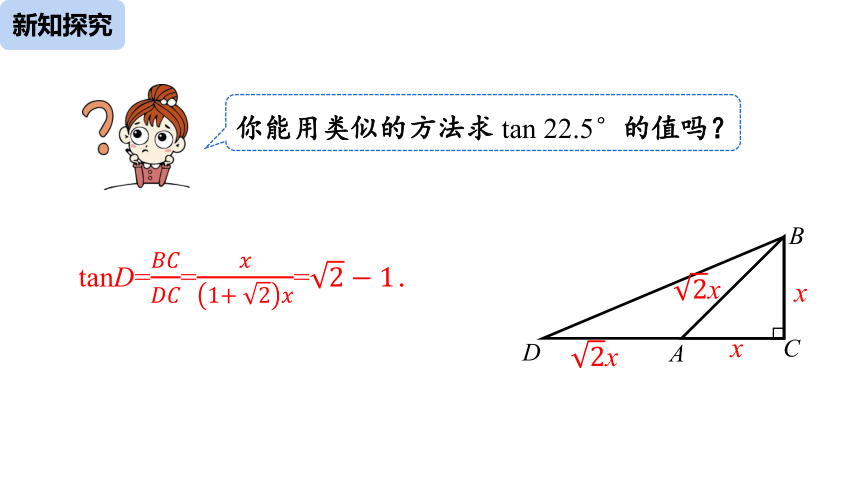
tanD=????????????????=????1+2????=2?1.
?
你能用类似的方法求 tan 22.5°的值吗?
新知探究
利用参数法求锐角三角函数值
当已知锐角 α 的一个三角函数值求锐角 α 的其他三角函数值时:
1.画出锐角 α 所在的直角三角形;
2.利用已知的三角函数值,通过采用设参数的方法,并结合勾股定理表示出三角形的三条边的长;
3.根据锐角三角函数的定义求解.
新知探究
2.已知,如图,⊙O 的半径 OA=4,弦 AB= 43,求劣弧
AB 的长.
?
O
A
B
解:连接OB,过点 O 作 AB 的垂线,
垂足为点 D,则点 D 为 AB 的中点,
∵ AB=43?,∴AD=23?,
在Rt△OAD中,sin∠AOD=????????????????=234=32,
∴∠AOD=60°,∴∠AOB=120°,
∴劣弧AB的长=120×????×4180=83?π.
?
D
新知探究
3.如图,钝角三角形 ABC 中,AC=12 cm,AB=16 cm,sinA
=13 .求 tan B 的值.
?
A
C
B
D
解:过点 C 作 AB 的垂线,垂足为点 D,
在Rt△ACD中,sinA=????????????????=????????12=13,
∴CD =4cm,则 ????????=????????2?????????2=82cm,
则 BD =AB-AD =16-82cm,
∴在Rt△BCD中,tanB=????????????????=416?82=2+24.
?
新知探究
构造直角三角形求锐角三角函数值
锐角三角函数是在直角三角形的条件下定义的,因此当题目要求某一个锐角的三角函数值时,要先观察这个锐角是否在某一个直角三角形中,当这个锐角不在直角三角形中时,一般可以先通过作辅助线构造与该角有关的直角三角形,再利用锐角三角函数的定义进行求解.
新知探究
求一个锐角的三角函数的实质是求什么?
实质是求边长的比.
可以转化为边长的比.
已知一个锐角的三角函数值可以转化为怎样的条件?
跟踪训练
如图,已知钝角三角形 ABC,点 D 在 BC 的延长线上,连接 AD,若∠ACB =2∠D,AD =2,AC= 32 ,求 sin D 的值.
?
B
A
D
C
B
A
D
C
跟踪训练
解:过点 C 作 CH⊥AD 于点 H.
∵ ∠ACB =2∠D,∠ACB =∠D +∠CAD,
∴ ∠D =∠CAD,
∴ CD =AC =32,AH =HD =1,
∴ CH = ????????2?????????2=322?12=52 ,
?
sin D = ????????????????=5232=53.
?
H
随堂练习
1.如图,△ABC 的顶点是正方形网格的格点,则 sin A 的值为( )
D
????
?
????????
?
A.12
?
B.55
?
C.1010
?
D.255
?
B
本题源自《教材帮》
在网格中求锐角三角函数值的方法
在网格中求某一锐角的三角函数值时,先借助网格的特点,利用勾股定理求出三角形的各边长,然后利用勾股定理的逆定理判断该三角形是否为直角三角形.若是,再利用锐角三角函数的定义求出三角函数值;若不是,则需作辅助线构造直角三角形.当锐角所在的直角三角形的各边不能求出时,可利用等角转换法进行求解.
随堂练习
随堂练习
2.如图是墙壁上在 l1,l2 两条平行线间边长为 a 的正方形瓷砖,该瓷砖与平行线的较大夹角为 α ,则两条平行线间的距离为( )
A.asinα
B.asinα+acosα
C.2acosα
D.asinα-acosα
B
D
C
A
随堂练习
解:过 B 作 EF⊥l1于点 E,EF⊥l2于点 F ,
∵ 四边形 ABCD 是正方形,
∴ AB=BC=a,∠ABC =90°,
∴∠ABE +∠CBF =∠ABE+∠BAE=90°,
∴∠BAE=∠CBF,
∵∠AEB=∠BFC=90°,
∴△ABE≌△BCF (AAS),
∴ BE =CF,
F
E
B
D
C
A
随堂练习
在 Rt△BCF 中,BF =a·sinα,CF=a·cosα,
∴ BE =a·cosα,
∴ EF=BE+BF=asinα+acosα,
即两条平行线间的距离为 asinα+acosα .
F
E
B
D
C
A
随堂练习
3.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=43,则CD的值为.
?
O
4
3
2
5
在Rt△OCD中,sin O =????????????????=????????2
?
在Rt△OAB中,sin O =????????????????=35
?
65
?
2
课堂小结
求一个锐角的三角函数的实质是求边长的比.
已知一个锐角的三角函数值可以转化为边长的比.
在非直角三角形中,可以通过添加辅助线,构造直角三角形,结合三角函数解决问题.
1
2
3
对接中考
1.(2020·安徽中考)如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cosA=45,则BD的长度为( )
A. 94 B. 125
C. 154 D. 4
?
????????=????????????????????????=5
?
4
????????=????????????????????????=????????????
?
C
3
A
D
C
B
对接中考
2.(2020·菏泽中考)如图,在△ABC 中,∠ACB =90°,点 D 为 AB 边的中点,连接 CD,若 BC =4,CD =3,则 cos∠DCB 的值为 .
解析:过点D作DE⊥BC,垂足为点E,
∵∠ACB=90°,DE⊥BC,
∴DE//AC,又∵点D为AB边的中点,
∴BE=EC=12BC=2,
在Rt△DCE中,cos∠DCB=????????????????=23 .
?
23
?
E
A
B
D
C
对接中考
2.(2020·菏泽中考)如图,在△ABC 中,∠ACB =90°,点 D 为 AB 边的中点,连接 CD,若 BC =4,CD =3,则 cos∠DCB 的值为 .
23
?
A
B
D
C
4
3
3
3
cos∠DCB= cos∠ABC=????????????????=46=23.
?
对接中考
3.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则????????????????=,tan∠APD=.
?
△ACP∽△BDP
B
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
C
A
D
P
????????????????=????????????????=31
?
3
3.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则????????????????=,tan∠APD=.
?
对接中考
DP=PF= 12 CF= 12 BF
?
B
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
C
A
D
P
E
F
tan∠APD= tan∠BPF=????????????????=2
?
2
3
课后作业
请完成课本后练习第2题.
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
如图,在 Rt△ABC 中,∠C=90°,
∠A 的 叫做∠A的正弦,
对边与斜边的比
∠A的对边斜边=????????????????
?
即 sin A = .
A
B
C
∠A 的邻边
∠A 的
对边
斜边
知识回顾
∠A的邻边
斜边
∠A 的 叫做∠A的余弦,
即 cos A = .
邻边与斜边的比
即 tan A = .
∠A的对边
∠A的邻边
对边与邻边的比
∠A 的 叫做∠A的正切,
A
B
C
∠A 的邻边
∠A 的
对边
斜边
学习目标
2.能根据锐角三角函数的定义解决与直角三角形有关的简单计算.
1.进一步认识锐角正弦、余弦和正切.
课堂导入
通过前面的学习,我们知道在直角三角形中,利用三角函数可以求出相关边长和角的度数,那么,在其他图形中我们能利用三角函数解决问题吗?
新知探究
知识点:利用三角函数解决问题
1.如图,在 Rt△ABC 中,∠C=90°,∠BAC=30°,延长 CA 至 D 点,使 AD=AB.
(1)求∠D;
(2)求tan D 的值.
D
A
C
B
解: (1) ∵ AB =AD,
∴ ∠D =∠ABD,
∵ ∠BAC =∠D +∠ABD =30°,
∴ ∠D =15°.
新知探究
解:(2)设BC=x,在Rt△ABC中,∵sin∠BAC=????????????????,
∴AB=????sin30°=2x,
∴AC=2????2?????2=3x,
∴CD=AD+AC=2x+3x=(2+3)x,
在Rt△BDC中,tanD=????????????????=????2+3????=2-3,
∴tan15°=2-3.
?
D
A
C
B
新知探究
D
A
C
B
x
x
2x
?
2x
?
tanD=????????????????=????1+2????=2?1.
?
你能用类似的方法求 tan 22.5°的值吗?
新知探究
利用参数法求锐角三角函数值
当已知锐角 α 的一个三角函数值求锐角 α 的其他三角函数值时:
1.画出锐角 α 所在的直角三角形;
2.利用已知的三角函数值,通过采用设参数的方法,并结合勾股定理表示出三角形的三条边的长;
3.根据锐角三角函数的定义求解.
新知探究
2.已知,如图,⊙O 的半径 OA=4,弦 AB= 43,求劣弧
AB 的长.
?
O
A
B
解:连接OB,过点 O 作 AB 的垂线,
垂足为点 D,则点 D 为 AB 的中点,
∵ AB=43?,∴AD=23?,
在Rt△OAD中,sin∠AOD=????????????????=234=32,
∴∠AOD=60°,∴∠AOB=120°,
∴劣弧AB的长=120×????×4180=83?π.
?
D
新知探究
3.如图,钝角三角形 ABC 中,AC=12 cm,AB=16 cm,sinA
=13 .求 tan B 的值.
?
A
C
B
D
解:过点 C 作 AB 的垂线,垂足为点 D,
在Rt△ACD中,sinA=????????????????=????????12=13,
∴CD =4cm,则 ????????=????????2?????????2=82cm,
则 BD =AB-AD =16-82cm,
∴在Rt△BCD中,tanB=????????????????=416?82=2+24.
?
新知探究
构造直角三角形求锐角三角函数值
锐角三角函数是在直角三角形的条件下定义的,因此当题目要求某一个锐角的三角函数值时,要先观察这个锐角是否在某一个直角三角形中,当这个锐角不在直角三角形中时,一般可以先通过作辅助线构造与该角有关的直角三角形,再利用锐角三角函数的定义进行求解.
新知探究
求一个锐角的三角函数的实质是求什么?
实质是求边长的比.
可以转化为边长的比.
已知一个锐角的三角函数值可以转化为怎样的条件?
跟踪训练
如图,已知钝角三角形 ABC,点 D 在 BC 的延长线上,连接 AD,若∠ACB =2∠D,AD =2,AC= 32 ,求 sin D 的值.
?
B
A
D
C
B
A
D
C
跟踪训练
解:过点 C 作 CH⊥AD 于点 H.
∵ ∠ACB =2∠D,∠ACB =∠D +∠CAD,
∴ ∠D =∠CAD,
∴ CD =AC =32,AH =HD =1,
∴ CH = ????????2?????????2=322?12=52 ,
?
sin D = ????????????????=5232=53.
?
H
随堂练习
1.如图,△ABC 的顶点是正方形网格的格点,则 sin A 的值为( )
D
????
?
????????
?
A.12
?
B.55
?
C.1010
?
D.255
?
B
本题源自《教材帮》
在网格中求锐角三角函数值的方法
在网格中求某一锐角的三角函数值时,先借助网格的特点,利用勾股定理求出三角形的各边长,然后利用勾股定理的逆定理判断该三角形是否为直角三角形.若是,再利用锐角三角函数的定义求出三角函数值;若不是,则需作辅助线构造直角三角形.当锐角所在的直角三角形的各边不能求出时,可利用等角转换法进行求解.
随堂练习
随堂练习
2.如图是墙壁上在 l1,l2 两条平行线间边长为 a 的正方形瓷砖,该瓷砖与平行线的较大夹角为 α ,则两条平行线间的距离为( )
A.asinα
B.asinα+acosα
C.2acosα
D.asinα-acosα
B
D
C
A
随堂练习
解:过 B 作 EF⊥l1于点 E,EF⊥l2于点 F ,
∵ 四边形 ABCD 是正方形,
∴ AB=BC=a,∠ABC =90°,
∴∠ABE +∠CBF =∠ABE+∠BAE=90°,
∴∠BAE=∠CBF,
∵∠AEB=∠BFC=90°,
∴△ABE≌△BCF (AAS),
∴ BE =CF,
F
E
B
D
C
A
随堂练习
在 Rt△BCF 中,BF =a·sinα,CF=a·cosα,
∴ BE =a·cosα,
∴ EF=BE+BF=asinα+acosα,
即两条平行线间的距离为 asinα+acosα .
F
E
B
D
C
A
随堂练习
3.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=43,则CD的值为.
?
O
4
3
2
5
在Rt△OCD中,sin O =????????????????=????????2
?
在Rt△OAB中,sin O =????????????????=35
?
65
?
2
课堂小结
求一个锐角的三角函数的实质是求边长的比.
已知一个锐角的三角函数值可以转化为边长的比.
在非直角三角形中,可以通过添加辅助线,构造直角三角形,结合三角函数解决问题.
1
2
3
对接中考
1.(2020·安徽中考)如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cosA=45,则BD的长度为( )
A. 94 B. 125
C. 154 D. 4
?
????????=????????????????????????=5
?
4
????????=????????????????????????=????????????
?
C
3
A
D
C
B
对接中考
2.(2020·菏泽中考)如图,在△ABC 中,∠ACB =90°,点 D 为 AB 边的中点,连接 CD,若 BC =4,CD =3,则 cos∠DCB 的值为 .
解析:过点D作DE⊥BC,垂足为点E,
∵∠ACB=90°,DE⊥BC,
∴DE//AC,又∵点D为AB边的中点,
∴BE=EC=12BC=2,
在Rt△DCE中,cos∠DCB=????????????????=23 .
?
23
?
E
A
B
D
C
对接中考
2.(2020·菏泽中考)如图,在△ABC 中,∠ACB =90°,点 D 为 AB 边的中点,连接 CD,若 BC =4,CD =3,则 cos∠DCB 的值为 .
23
?
A
B
D
C
4
3
3
3
cos∠DCB= cos∠ABC=????????????????=46=23.
?
对接中考
3.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则????????????????=,tan∠APD=.
?
△ACP∽△BDP
B
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
C
A
D
P
????????????????=????????????????=31
?
3
3.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则????????????????=,tan∠APD=.
?
对接中考
DP=PF= 12 CF= 12 BF
?
B
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
C
A
D
P
E
F
tan∠APD= tan∠BPF=????????????????=2
?
2
3
课后作业
请完成课本后练习第2题.
