人教版数学九年级下册28.1 锐角三角函数 课时2课件(34张)
文档属性
| 名称 | 人教版数学九年级下册28.1 锐角三角函数 课时2课件(34张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 23:46:25 | ||
图片预览






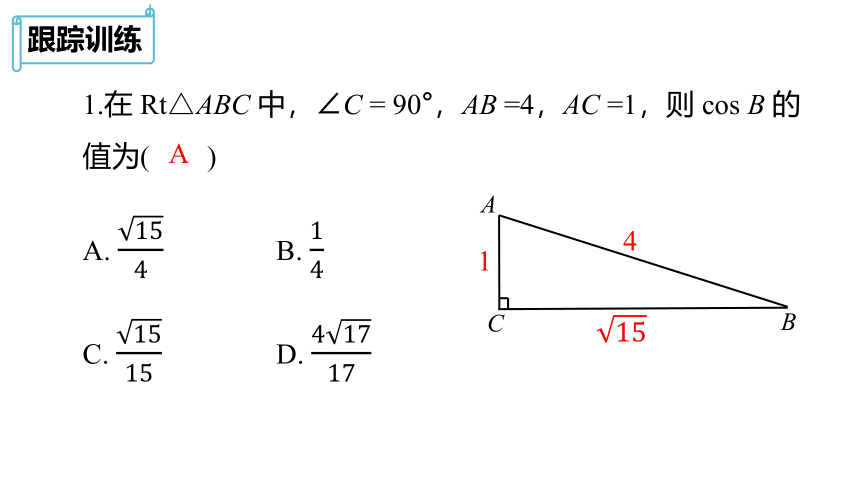
文档简介
28.1 锐角三角函数
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
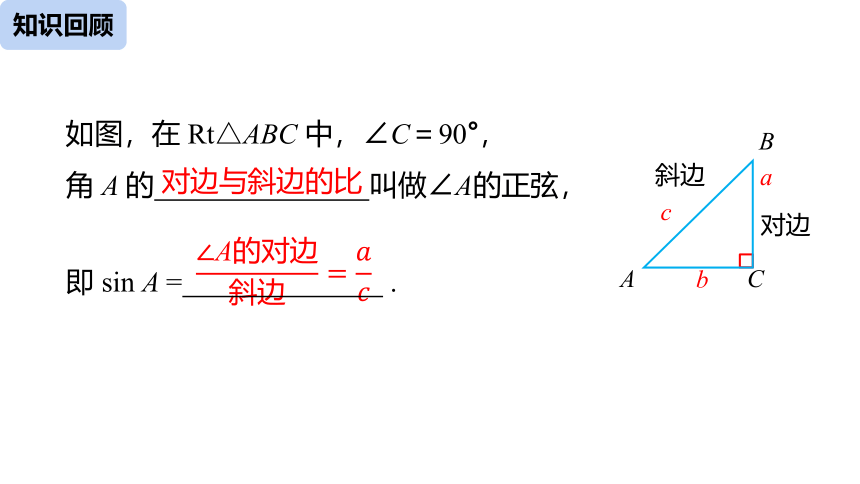
如图,在 Rt△ABC 中,∠C=90°,
角 A 的 叫做∠A的正弦,
对边与斜边的比
∠A的对边斜边=????????
?
即 sin A = .
A
B
C
c
a
b
对边
斜边
学习目标
1.认识并理解余弦、正切的概念,进而得到锐角三角函数的概念.
2.能灵活运用锐角三角函数进行相关运算.
课堂导入
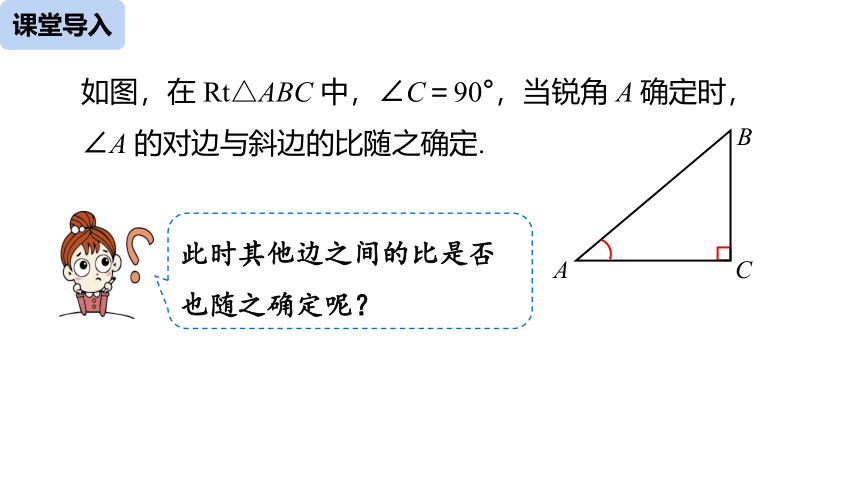
如图,在 Rt△ABC 中,∠C=90°,当锐角 A 确定时,∠A 的对边与斜边的比随之确定.
A
B
C
此时其他边之间的比是否
也随之确定呢?
新知探究
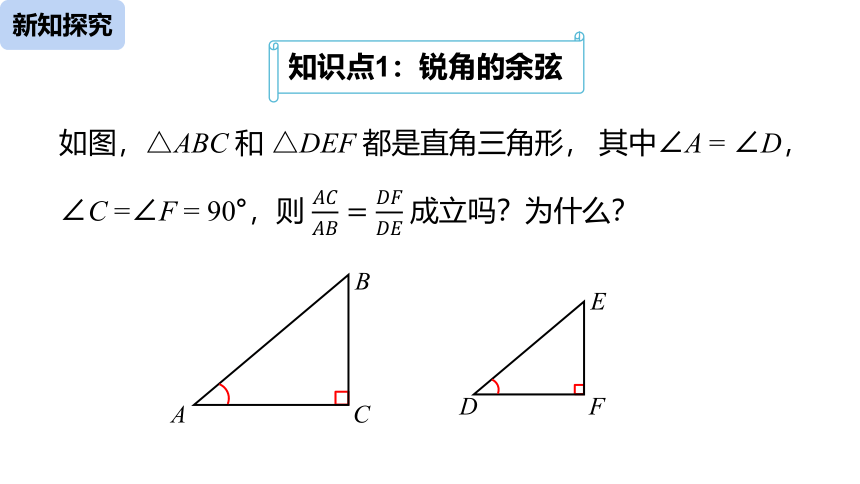
知识点1:锐角的余弦
如图,△ABC 和 △DEF 都是直角三角形, 其中∠A = ∠D,∠C =∠F = 90°,则 ????????????????=???????????????? 成立吗?为什么?
?
A
B
C
D
E
F
新知探究
∵
∠A=∠D,∠C=∠F=90°,
∴
∠B=∠E,
∴sinB = sinE,
因此
A
B
C
D
E
F
在有一个锐角相等的所有直角三角形中,这个锐角的邻边与斜边的比值是一个常数,与直角三角形的大小无关.
新知探究
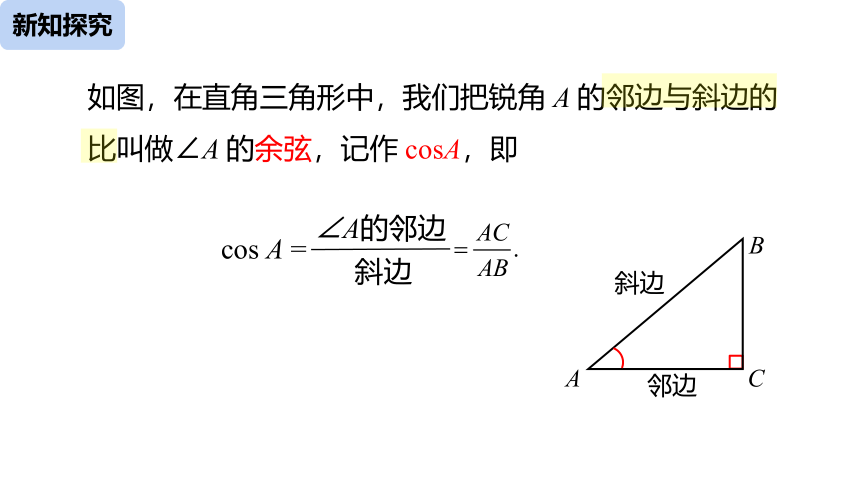
如图,在直角三角形中,我们把锐角 A 的邻边与斜边的比叫做∠A 的余弦,记作 cosA,即
A
B
C
斜边
邻边
∠A的邻边
斜边
cos A =
新知探究
1.余弦是在直角三角形中定义的,反映了直角三角形边与角的关系.
2.余弦是一个比值,是两条线段长度的比,是没有单位的数值,它只与锐角的大小有关,而与三角形的大小无关.
新知探究
A
B
C
4
3
图①
解:如图①,在 Rt△ABC 中,由勾股定理得
因此
确定角的邻边和斜边
如图,在 Rt△ABC 中,∠C=90°,求 cosA 和 cosB 的值.
新知探究
A
B
C
13
5
图②
解:如图②,在Rt△ABC中,由勾股定理得
因此
确定角的邻边和斜边
如图,在 Rt△ABC 中,∠C=90°,求 cosA 和 cosB 的值.
跟踪训练
1.在 Rt△ABC 中,∠C = 90°,AB =4,AC =1,则 cos B 的
值为( )
A. 154 B. 14
C. 1515 D. 41717
?
A
B
C
1
4
15
?
A
跟踪训练
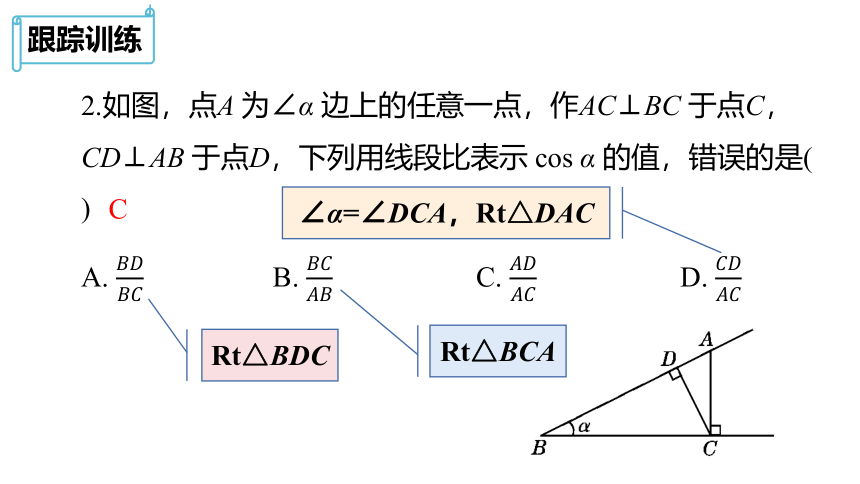
2.如图,点A 为∠α 边上的任意一点,作AC⊥BC 于点C,CD⊥AB 于点D,下列用线段比表示 cos α 的值,错误的是( )
A. ???????????????? B. ???????????????? C. ???????????????? D. ????????????????
?
C
Rt△BDC
Rt△BCA
∠α=∠DCA,Rt△DAC
新知探究
知识点2:锐角的正切
如图,△ABC 和 △DEF 都是直角三角形, 其中∠A =∠D,∠C = ∠F = 90°,则 ????????????????=???????????????? 成立吗?为什么?
?
A
B
C
D
E
F
新知探究
∴ Rt△ABC ∽ Rt△DEF.
即 BC · DF = AC · EF ,
∠A=∠D ,∠C =∠F = 90°,
∵
∴
∴
A
B
C
D
E
F
在有一个锐角相等的所有直角三角形中,这个锐角的对边与邻边的比值是一个常数,与直角三角形的大小无关.
新知探究
如图,在直角三角形中,我们把锐角 A 的对边与邻边的比叫做 ∠A 的正切,记作 tanA, 即
∠A的邻边
∠A的对边
tan A =
A
B
C
邻边
对边
新知探究
1.正切是在直角三角形中定义的,反映了直角三角形边与角的关系.
2.正切是一个比值,是两条线段长度的比,是没有单位的数值,它只与锐角的大小有关,而与三角形的大小无关.
新知探究
活学巧记
锐角三角函数值,正弦等于对比斜,
余弦等于邻比斜,正切等于对比邻,
由于都是两边比,因此其值都为正.
新知探究
∠A 的正弦、余弦、正切都是∠A 的锐角三角函数.
对于锐角 A 的每一个确定的值,sin A 有唯一确定的值与它对应,所以 sin A 是 A 的函数.同样地,cos A,tan A 也是 A 的函数.
由于直角三角形的斜边大于直角边,且各边的边长均为正数,所以锐角三角函数值都是正实数,且0< sin A <1,0< cos A <1,tan A >0.
新知探究
例2 如图,在 Rt△ABC 中,∠C =90°,AB =10,BC =6,求 sin A,cos A,tan A 的值.
A
B
C
10
6
解:由勾股定理得
因此
新知探究
A
B
C
6
如图,在 Rt△ABC 中,∠C = 90°,BC = 6, sin A = 35,求 cosA、tanB 的值.
?
解:∵
又
∴
∴
跟踪训练
分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
5
分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
13
?
跟踪训练
随堂练习
1.如图,在 4×4 的小正方形方格图形中,小正方形的顶点称为格点,△ABC 的顶点都在格点上,则图中∠ABC 的余弦值是( )
A. 2B. 255
C. 12D. 55
?
解析:设小正方形的边长为1,由图可知,
AC= 22+42 = 25 ,BC= 12+22 = 5 ,AB= 32+42 =5,
∴ AC2 +BC2 =AB2,
∴ △ABC 是直角三角形,且∠ACB =90°,
∴ cos∠ABC = ????????????????=55.
?
随堂练习
随堂练习
2.如图,在半径为 3 的⊙O 中,直径 AB 与弦 CD 相交于点 E,连接 AC,BD,若 AC = 2,则 tan D = .
1.直径所对的圆周角为直角;
2.同弧或等弧所对的圆周角相等.
随堂练习
2.如图,在半径为 3 的⊙O 中,直径 AB 与弦 CD 相交于点 E,连接 AC,BD,若 AC = 2,则 tan D = .
解析:如图所示,连接 BC.
∵ AB 为⊙O 的直径,∴∠ACB =90°.
又 AB =6,∴ BC =????????2?????????2=62?22=42.
∵ ∠D =∠A,∴ tan D =tan A = ????????????????=422=22 .
?
22
?
随堂练习
3.已知 α是锐角,且 cos α= 45 ,求 sin α, tan α的值.
?
3k
5k
4k
????????????????=????????
?
随堂练习
利用参数法求锐角三角函数值
当已知锐角 α 的一个三角函数值求锐角 α 的其他三角函数值时,可先画出锐角 α 所在的直角三角形,然后利用已知的三角函数值,通过采用设参数的方法,并结合勾股定理表示出三角形的三条边的长,再根据锐角三角函数的定义求解.
课堂小结
∠A的对边
斜边
sin A =
三角函数
正弦
∠A的邻边
斜边
cos A =
余弦
∠A的对边
∠A的邻边
tan A =
正切
对接中考
1.(2020·杭州中考)如图,在△ABC 中,∠C =90°,设∠A,∠B,∠C 所对的边分别为 a,b,c,则( )
A.c=b·sin B
B.b=c·sin B
C.a=b·tan B
D.b=c·tan B
B
C
A
B
对接中考
2.(2018·滨州中考)在△ABC中,∠C=90°,若tanA=12,则sinB=.
?
k
5k
?
2k
????????????????=????????
?
A
B
C
255
?
对接中考
3.(2019·杭州中考)在直角三角形 ABC 中,若 2AB =AC,则cos C = .
k
3k
?
2k
C
A
B
∠B =90°
k
5k
?
2k
C
B
A
对接中考
还有可能∠A =90°
此题容易考虑问题不全面,即只考虑到∠B =90°或∠A =90°,而漏掉另外一种情况.有效杜绝此类错误产生的方法是依据题意绘制图形.
课后作业
请完成课本后习题第1题.
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
如图,在 Rt△ABC 中,∠C=90°,
角 A 的 叫做∠A的正弦,
对边与斜边的比
∠A的对边斜边=????????
?
即 sin A = .
A
B
C
c
a
b
对边
斜边
学习目标
1.认识并理解余弦、正切的概念,进而得到锐角三角函数的概念.
2.能灵活运用锐角三角函数进行相关运算.
课堂导入
如图,在 Rt△ABC 中,∠C=90°,当锐角 A 确定时,∠A 的对边与斜边的比随之确定.
A
B
C
此时其他边之间的比是否
也随之确定呢?
新知探究
知识点1:锐角的余弦
如图,△ABC 和 △DEF 都是直角三角形, 其中∠A = ∠D,∠C =∠F = 90°,则 ????????????????=???????????????? 成立吗?为什么?
?
A
B
C
D
E
F
新知探究
∵
∠A=∠D,∠C=∠F=90°,
∴
∠B=∠E,
∴sinB = sinE,
因此
A
B
C
D
E
F
在有一个锐角相等的所有直角三角形中,这个锐角的邻边与斜边的比值是一个常数,与直角三角形的大小无关.
新知探究
如图,在直角三角形中,我们把锐角 A 的邻边与斜边的比叫做∠A 的余弦,记作 cosA,即
A
B
C
斜边
邻边
∠A的邻边
斜边
cos A =
新知探究
1.余弦是在直角三角形中定义的,反映了直角三角形边与角的关系.
2.余弦是一个比值,是两条线段长度的比,是没有单位的数值,它只与锐角的大小有关,而与三角形的大小无关.
新知探究
A
B
C
4
3
图①
解:如图①,在 Rt△ABC 中,由勾股定理得
因此
确定角的邻边和斜边
如图,在 Rt△ABC 中,∠C=90°,求 cosA 和 cosB 的值.
新知探究
A
B
C
13
5
图②
解:如图②,在Rt△ABC中,由勾股定理得
因此
确定角的邻边和斜边
如图,在 Rt△ABC 中,∠C=90°,求 cosA 和 cosB 的值.
跟踪训练
1.在 Rt△ABC 中,∠C = 90°,AB =4,AC =1,则 cos B 的
值为( )
A. 154 B. 14
C. 1515 D. 41717
?
A
B
C
1
4
15
?
A
跟踪训练
2.如图,点A 为∠α 边上的任意一点,作AC⊥BC 于点C,CD⊥AB 于点D,下列用线段比表示 cos α 的值,错误的是( )
A. ???????????????? B. ???????????????? C. ???????????????? D. ????????????????
?
C
Rt△BDC
Rt△BCA
∠α=∠DCA,Rt△DAC
新知探究
知识点2:锐角的正切
如图,△ABC 和 △DEF 都是直角三角形, 其中∠A =∠D,∠C = ∠F = 90°,则 ????????????????=???????????????? 成立吗?为什么?
?
A
B
C
D
E
F
新知探究
∴ Rt△ABC ∽ Rt△DEF.
即 BC · DF = AC · EF ,
∠A=∠D ,∠C =∠F = 90°,
∵
∴
∴
A
B
C
D
E
F
在有一个锐角相等的所有直角三角形中,这个锐角的对边与邻边的比值是一个常数,与直角三角形的大小无关.
新知探究
如图,在直角三角形中,我们把锐角 A 的对边与邻边的比叫做 ∠A 的正切,记作 tanA, 即
∠A的邻边
∠A的对边
tan A =
A
B
C
邻边
对边
新知探究
1.正切是在直角三角形中定义的,反映了直角三角形边与角的关系.
2.正切是一个比值,是两条线段长度的比,是没有单位的数值,它只与锐角的大小有关,而与三角形的大小无关.
新知探究
活学巧记
锐角三角函数值,正弦等于对比斜,
余弦等于邻比斜,正切等于对比邻,
由于都是两边比,因此其值都为正.
新知探究
∠A 的正弦、余弦、正切都是∠A 的锐角三角函数.
对于锐角 A 的每一个确定的值,sin A 有唯一确定的值与它对应,所以 sin A 是 A 的函数.同样地,cos A,tan A 也是 A 的函数.
由于直角三角形的斜边大于直角边,且各边的边长均为正数,所以锐角三角函数值都是正实数,且0< sin A <1,0< cos A <1,tan A >0.
新知探究
例2 如图,在 Rt△ABC 中,∠C =90°,AB =10,BC =6,求 sin A,cos A,tan A 的值.
A
B
C
10
6
解:由勾股定理得
因此
新知探究
A
B
C
6
如图,在 Rt△ABC 中,∠C = 90°,BC = 6, sin A = 35,求 cosA、tanB 的值.
?
解:∵
又
∴
∴
跟踪训练
分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
5
分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.
13
?
跟踪训练
随堂练习
1.如图,在 4×4 的小正方形方格图形中,小正方形的顶点称为格点,△ABC 的顶点都在格点上,则图中∠ABC 的余弦值是( )
A. 2B. 255
C. 12D. 55
?
解析:设小正方形的边长为1,由图可知,
AC= 22+42 = 25 ,BC= 12+22 = 5 ,AB= 32+42 =5,
∴ AC2 +BC2 =AB2,
∴ △ABC 是直角三角形,且∠ACB =90°,
∴ cos∠ABC = ????????????????=55.
?
随堂练习
随堂练习
2.如图,在半径为 3 的⊙O 中,直径 AB 与弦 CD 相交于点 E,连接 AC,BD,若 AC = 2,则 tan D = .
1.直径所对的圆周角为直角;
2.同弧或等弧所对的圆周角相等.
随堂练习
2.如图,在半径为 3 的⊙O 中,直径 AB 与弦 CD 相交于点 E,连接 AC,BD,若 AC = 2,则 tan D = .
解析:如图所示,连接 BC.
∵ AB 为⊙O 的直径,∴∠ACB =90°.
又 AB =6,∴ BC =????????2?????????2=62?22=42.
∵ ∠D =∠A,∴ tan D =tan A = ????????????????=422=22 .
?
22
?
随堂练习
3.已知 α是锐角,且 cos α= 45 ,求 sin α, tan α的值.
?
3k
5k
4k
????????????????=????????
?
随堂练习
利用参数法求锐角三角函数值
当已知锐角 α 的一个三角函数值求锐角 α 的其他三角函数值时,可先画出锐角 α 所在的直角三角形,然后利用已知的三角函数值,通过采用设参数的方法,并结合勾股定理表示出三角形的三条边的长,再根据锐角三角函数的定义求解.
课堂小结
∠A的对边
斜边
sin A =
三角函数
正弦
∠A的邻边
斜边
cos A =
余弦
∠A的对边
∠A的邻边
tan A =
正切
对接中考
1.(2020·杭州中考)如图,在△ABC 中,∠C =90°,设∠A,∠B,∠C 所对的边分别为 a,b,c,则( )
A.c=b·sin B
B.b=c·sin B
C.a=b·tan B
D.b=c·tan B
B
C
A
B
对接中考
2.(2018·滨州中考)在△ABC中,∠C=90°,若tanA=12,则sinB=.
?
k
5k
?
2k
????????????????=????????
?
A
B
C
255
?
对接中考
3.(2019·杭州中考)在直角三角形 ABC 中,若 2AB =AC,则cos C = .
k
3k
?
2k
C
A
B
∠B =90°
k
5k
?
2k
C
B
A
对接中考
还有可能∠A =90°
此题容易考虑问题不全面,即只考虑到∠B =90°或∠A =90°,而漏掉另外一种情况.有效杜绝此类错误产生的方法是依据题意绘制图形.
课后作业
请完成课本后习题第1题.
