人教版数学九年级下册28.2.2 应用举例 课时1课件(28张)
文档属性
| 名称 | 人教版数学九年级下册28.2.2 应用举例 课时1课件(28张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览






文档简介
28.2.2 应用举例
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
(1) 三边之间的关系:
a2+b2=c2(勾股定理);
解直角三角形的依据有哪些?
(2) 两锐角之间的关系:
∠ A +∠ B = 90?;
(3) 边角之间的关系:
sinA=
a
c
A
C
B
a
b
c
cosA=
b
c
tanA=
a
b
学习目标
1.巩固解直角三角形的相关知识.
2.能从实际问题中构造直角三角形,从而把实际问题转化为解直角三角形的问题,并能灵活选择三角函数解决问题.
课堂导入
人体工程学研究人员发现若成年人的脚掌长为 15 cm,鞋跟高度约在 3 cm左右为最佳. 据此,可以算出高跟鞋的鞋底与地面的夹角为 11°左右时,人脚的感觉最舒适.
你知道这是怎么计算的吗?
新知探究
知识点:利用解直角三角形解决实际问题
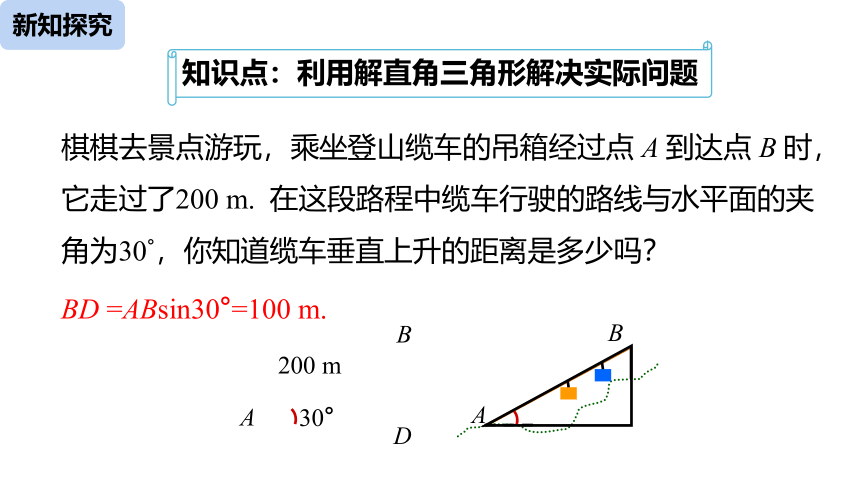
棋棋去景点游玩,乘坐登山缆车的吊箱经过点 A 到达点 B 时,它走过了200 m. 在这段路程中缆车行驶的路线与水平面的夹角为30°,你知道缆车垂直上升的距离是多少吗?
A
B
A
B
D
30°
200 m
BD =ABsin30°=100 m.
新知探究
A
B
C
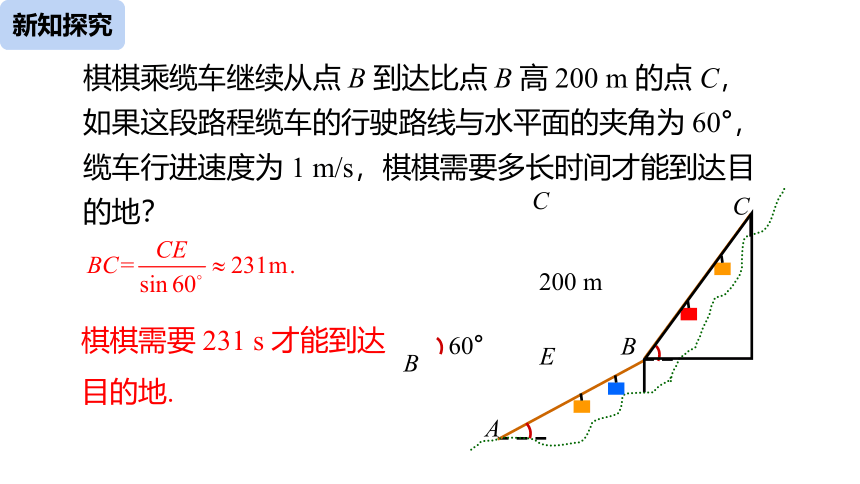
棋棋乘缆车继续从点 B 到达比点 B 高 200 m 的点 C, 如果这段路程缆车的行驶路线与水平面的夹角为 60°,缆车行进速度为 1 m/s,棋棋需要多长时间才能到达目的地?
C
E
60°
200 m
棋棋需要 231 s 才能到达目的地.
B
新知探究
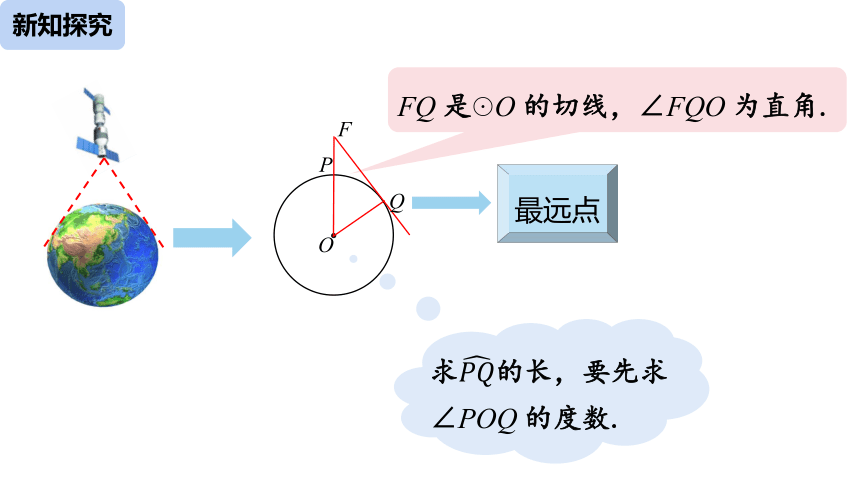
例3 2012年6月18日,“神州”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接. “神州”九号与“天宫”一号的组合体在离地球表面 343 km 的圆形轨道上运行. 如图,当组合体运行到地球表面 P 点的正上方
时,从中能直接看到的地球表面最远的点
在什么位置?最远点与 P 点的距离是多少
(地球半径约为 6400 km,π 取 3.142,结果
取整数)?
新知探究
FQ 是☉O 的切线,∠FQO 为直角.
O
F
P
Q
最远点
求????????的长,要先求∠POQ 的度数.
?
新知探究
利用解直角三角形解决实际问题的一般过程:
将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
根据问题中的条件,选用合适的锐角三角函数解直角三角形;
得到数学问题的答案;
得到实际问题的答案.
1
2
3
4
新知探究
1.当实际问题中涉及的图形可以直接转化为直角三角形时,可利用解直角三角形的知识直接求解.
2.数学问题的解符合实际意义才可以成为实际问题的解.
新知探究
如图,秋千链子的长度为 3 m,静止时的秋千踏板(大小忽略不计)距地面 0.5 m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为 53°,则秋千踏板与地面的最大距离约为多少?
(参考数据:sin53°≈0.8,cos53°≈0.6)
0.5m
3m
53°
新知探究
解:如图,设秋千链子的上端固定于A处,秋千踏板摆动到最高位置时踏板位于B处.过点A,B的铅垂线分别为AD,BE,点D,E在地面上,过B作BC⊥AD于点C.
在Rt△ABC中,AB=3,∠CAB=53°,
∵cos53°=????????????????,
∴AC=3cos53°≈3×0.6=1.8m,
∴CD≈3+0.5-1.8=1.7m,
∴BE=CD≈1.7m,
答:秋千踏板与地面的最大距离约为1.7m.
?
0.5m
3m
A
B
C
D
E
53°
跟踪训练
图为放置在水平桌面上的台灯的平面示意图,灯臂 AO长为 40 cm,与水平面所形成的夹角∠OAM 为 75°.由光源 O 射出的边缘光线 OC,OB 与水平面所形成的夹角∠OCA,∠OBA 分别为90°和30°,求该台灯照亮水平面的宽度 BC.(不考虑其他因素,结果精确到 0.1 cm.参考数据:
sin75°≈0.97,cos75°≈0.26,3≈1.73)
?
解:在 Rt△AOC 中,sin75°=????????????????=????????40 ≈ 0.97,
解得 OC ≈ 38.8 cm.
在 Rt△BOC 中,tan30°=?????????????????=38.8????????≈1.733,
解得 BC ≈ 67.3 cm.
答:该台灯照亮水平面的宽度 BC 约为67.3 cm.
?
跟踪训练
注意结果必须根据题目要求精确到0.1cm.
借助公共边解双直角三角形
当实际问题的示意图中出现有公共直角边的两个直角三角形时,一般借助这条公共边“牵线搭桥”,即先在其中一个直角三角形中求出公共边,再在另一个直角三角形中根据所求得的公共边选用适当的三角函数进行求解.
跟踪训练
随堂练习
1.芜湖长江大桥是一座公路和铁路两用桥梁,如图(1),图(2)是从图(1)中引申出的平面图.假设拉索 AB 与水平桥面的夹角是 30°,拉索 CD 与水平桥面的夹角是 60°,两拉索顶端的距离 BC 为 2米.两拉索底端的距离 AD 为20米,请求出立柱 BH 的长.(结果精确到0.1米,3≈1.732)
?
随堂练习
解:设 DH =x 米. ∵ ∠CDH =60° ,∠H =90°,
∴ CH =DH·tan60°=3x 米,
∴ BH =BC +CH =(2+3 x)米.
∵∠A =30°, ∴ AH=????????tan30°=(23 +3x)米.
∵ AH =AD +DH,∴ 23 +3x=20+x,解得 x =10- 3.
∴ BH =2+ 3(10- 3)=10 3 -1≈16.3(米).
答:立柱 BH 的长约为16.3米.
?
随堂练习
2.某房地产集团筹建一小区,小区内居民楼南北朝向,楼高统一为 16 m(五层).已知该城市冬至正午时分太阳高度最低,太阳光线与水平线的夹角为32°,如果南、北两楼相隔仅有 20 m,如图所示.
(1)此时南楼的影子落在北楼上有多高?(已知 tan32°=0.6249)
(2)根据居住要求,每层楼在冬天都要受阳光照射,请你重新设计一下方案(结果精确到0.1 m)
随堂练习
解:(1)如图,过点 C 作 CE⊥AB 于点 E,
由题意可知∠ACE =32°,CE =BD =20 m.
在 Rt△ACE 中, ∵ tan∠ACE =????????????????,
∴ AE =CE·tan∠ACE =20·tan32°≈12.5(m),
∴ DC =EB =AB-AE =16-12.5=3.5(m),
∴ 此时南楼的影子落在北楼上约 3.5 m 高.
?
E
随堂练习
解:(2)如图,若使每层楼在冬天都受阳光照射,则 DC =0 m,即点 C 与点 D 重合.
当点 C 与点 D 重合时,tan∠ACB =????????????????,
即 tan32°=????????????????,
∴ BD= ????????tan32°=16tan32°≈25.6?(m),
∴ 重新设计时,两楼的距离至少应为 25.6 m 才能使每层楼在冬天都受阳光照射.
?
随堂练习
3.如图1,AB =EG =5,FG =10,AD =4,小红想用△EFG 包裹矩形 ABCD,她包裹的方法如图2所示,则矩形 ABCD 未包裹住的面积为 .
F
E
G
B
D
C
A
图1
图2
B
D
C(G)
A
E
F
B
D
C(G)
A
B′
C′
F
E
H
H
随堂练习
解:如图,将矩形ABCD以AD为轴翻折,将Rt△EFG 以EG 为轴翻折,则△B′C′H 即为未包裹住的面积,
∵Rt△HBE∽Rt△HB′C′,
∴????????????????′=????????????′????′,即10?????????′????????′=5?44,
解得HB′=8,
∴S△B′C′H=12·B′C′·B′H=12×4×8=16.
?
B
D
C(G)
A
B′
C′
F
E
H
课堂小结
利用解直角三角形解决实际问题的一般过程:
实际问题
数学问题
数学问题的答案
实际问题的答案
选用适当的锐角三角函数解直角三角形
对接中考
1.(2019·温州中考)某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆 AB 的长为( )
A. 95sin???? m B. 95cos???? m C. 59sin????? m D.59cos???? m
?
D
BD= 32+0.3=95
?
????????????????=????????????????
?
B
对接中考
2.(2020·长春中考)比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点B,塔身中心线AB与垂直中心线AC的夹角为∠A,过点B向垂直中心线AC引垂线,垂足为点D.通过测量可得AB、BD、AD的长度,利用测量所得的数据计算∠A的三角函数值,进而可求∠A的大小.下列关系式正确的是( )
sinA=???????????????? B.cosA=????????????????
C.tanA=????????????????? D. sinA=????????????????
?
解析:sinA=????????????????,cosA=?????????????????,tanA=?????????????????.
?
A
A
D
C
B
垂直中心线
塔身中心线
对接中考
3.(2020·孝感中考)某型号飞机的机翼形状如图所示,根据图中数据计算 AB 的长为 m.(结果保留根号)
解:如图,在Rt△DEA中,∵∠EDA=45°,
∴DE=AE=5?(m);
在Rt△BCF中,∵cos∠BCF=?????????????????,
∴CB=5cos30°?=1033?(m),∴BF=12?BC=533?(m),
∵AB+AE=EF+BF,
∴AB=3.4+533?5?=533?1.6(m).
?
F
E
533?1.6
?
D
5m
C
A
B
3.4m
45°
30°
课后作业
请完成课本后习题第2、7题.
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
(1) 三边之间的关系:
a2+b2=c2(勾股定理);
解直角三角形的依据有哪些?
(2) 两锐角之间的关系:
∠ A +∠ B = 90?;
(3) 边角之间的关系:
sinA=
a
c
A
C
B
a
b
c
cosA=
b
c
tanA=
a
b
学习目标
1.巩固解直角三角形的相关知识.
2.能从实际问题中构造直角三角形,从而把实际问题转化为解直角三角形的问题,并能灵活选择三角函数解决问题.
课堂导入
人体工程学研究人员发现若成年人的脚掌长为 15 cm,鞋跟高度约在 3 cm左右为最佳. 据此,可以算出高跟鞋的鞋底与地面的夹角为 11°左右时,人脚的感觉最舒适.
你知道这是怎么计算的吗?
新知探究
知识点:利用解直角三角形解决实际问题
棋棋去景点游玩,乘坐登山缆车的吊箱经过点 A 到达点 B 时,它走过了200 m. 在这段路程中缆车行驶的路线与水平面的夹角为30°,你知道缆车垂直上升的距离是多少吗?
A
B
A
B
D
30°
200 m
BD =ABsin30°=100 m.
新知探究
A
B
C
棋棋乘缆车继续从点 B 到达比点 B 高 200 m 的点 C, 如果这段路程缆车的行驶路线与水平面的夹角为 60°,缆车行进速度为 1 m/s,棋棋需要多长时间才能到达目的地?
C
E
60°
200 m
棋棋需要 231 s 才能到达目的地.
B
新知探究
例3 2012年6月18日,“神州”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接. “神州”九号与“天宫”一号的组合体在离地球表面 343 km 的圆形轨道上运行. 如图,当组合体运行到地球表面 P 点的正上方
时,从中能直接看到的地球表面最远的点
在什么位置?最远点与 P 点的距离是多少
(地球半径约为 6400 km,π 取 3.142,结果
取整数)?
新知探究
FQ 是☉O 的切线,∠FQO 为直角.
O
F
P
Q
最远点
求????????的长,要先求∠POQ 的度数.
?
新知探究
利用解直角三角形解决实际问题的一般过程:
将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
根据问题中的条件,选用合适的锐角三角函数解直角三角形;
得到数学问题的答案;
得到实际问题的答案.
1
2
3
4
新知探究
1.当实际问题中涉及的图形可以直接转化为直角三角形时,可利用解直角三角形的知识直接求解.
2.数学问题的解符合实际意义才可以成为实际问题的解.
新知探究
如图,秋千链子的长度为 3 m,静止时的秋千踏板(大小忽略不计)距地面 0.5 m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为 53°,则秋千踏板与地面的最大距离约为多少?
(参考数据:sin53°≈0.8,cos53°≈0.6)
0.5m
3m
53°
新知探究
解:如图,设秋千链子的上端固定于A处,秋千踏板摆动到最高位置时踏板位于B处.过点A,B的铅垂线分别为AD,BE,点D,E在地面上,过B作BC⊥AD于点C.
在Rt△ABC中,AB=3,∠CAB=53°,
∵cos53°=????????????????,
∴AC=3cos53°≈3×0.6=1.8m,
∴CD≈3+0.5-1.8=1.7m,
∴BE=CD≈1.7m,
答:秋千踏板与地面的最大距离约为1.7m.
?
0.5m
3m
A
B
C
D
E
53°
跟踪训练
图为放置在水平桌面上的台灯的平面示意图,灯臂 AO长为 40 cm,与水平面所形成的夹角∠OAM 为 75°.由光源 O 射出的边缘光线 OC,OB 与水平面所形成的夹角∠OCA,∠OBA 分别为90°和30°,求该台灯照亮水平面的宽度 BC.(不考虑其他因素,结果精确到 0.1 cm.参考数据:
sin75°≈0.97,cos75°≈0.26,3≈1.73)
?
解:在 Rt△AOC 中,sin75°=????????????????=????????40 ≈ 0.97,
解得 OC ≈ 38.8 cm.
在 Rt△BOC 中,tan30°=?????????????????=38.8????????≈1.733,
解得 BC ≈ 67.3 cm.
答:该台灯照亮水平面的宽度 BC 约为67.3 cm.
?
跟踪训练
注意结果必须根据题目要求精确到0.1cm.
借助公共边解双直角三角形
当实际问题的示意图中出现有公共直角边的两个直角三角形时,一般借助这条公共边“牵线搭桥”,即先在其中一个直角三角形中求出公共边,再在另一个直角三角形中根据所求得的公共边选用适当的三角函数进行求解.
跟踪训练
随堂练习
1.芜湖长江大桥是一座公路和铁路两用桥梁,如图(1),图(2)是从图(1)中引申出的平面图.假设拉索 AB 与水平桥面的夹角是 30°,拉索 CD 与水平桥面的夹角是 60°,两拉索顶端的距离 BC 为 2米.两拉索底端的距离 AD 为20米,请求出立柱 BH 的长.(结果精确到0.1米,3≈1.732)
?
随堂练习
解:设 DH =x 米. ∵ ∠CDH =60° ,∠H =90°,
∴ CH =DH·tan60°=3x 米,
∴ BH =BC +CH =(2+3 x)米.
∵∠A =30°, ∴ AH=????????tan30°=(23 +3x)米.
∵ AH =AD +DH,∴ 23 +3x=20+x,解得 x =10- 3.
∴ BH =2+ 3(10- 3)=10 3 -1≈16.3(米).
答:立柱 BH 的长约为16.3米.
?
随堂练习
2.某房地产集团筹建一小区,小区内居民楼南北朝向,楼高统一为 16 m(五层).已知该城市冬至正午时分太阳高度最低,太阳光线与水平线的夹角为32°,如果南、北两楼相隔仅有 20 m,如图所示.
(1)此时南楼的影子落在北楼上有多高?(已知 tan32°=0.6249)
(2)根据居住要求,每层楼在冬天都要受阳光照射,请你重新设计一下方案(结果精确到0.1 m)
随堂练习
解:(1)如图,过点 C 作 CE⊥AB 于点 E,
由题意可知∠ACE =32°,CE =BD =20 m.
在 Rt△ACE 中, ∵ tan∠ACE =????????????????,
∴ AE =CE·tan∠ACE =20·tan32°≈12.5(m),
∴ DC =EB =AB-AE =16-12.5=3.5(m),
∴ 此时南楼的影子落在北楼上约 3.5 m 高.
?
E
随堂练习
解:(2)如图,若使每层楼在冬天都受阳光照射,则 DC =0 m,即点 C 与点 D 重合.
当点 C 与点 D 重合时,tan∠ACB =????????????????,
即 tan32°=????????????????,
∴ BD= ????????tan32°=16tan32°≈25.6?(m),
∴ 重新设计时,两楼的距离至少应为 25.6 m 才能使每层楼在冬天都受阳光照射.
?
随堂练习
3.如图1,AB =EG =5,FG =10,AD =4,小红想用△EFG 包裹矩形 ABCD,她包裹的方法如图2所示,则矩形 ABCD 未包裹住的面积为 .
F
E
G
B
D
C
A
图1
图2
B
D
C(G)
A
E
F
B
D
C(G)
A
B′
C′
F
E
H
H
随堂练习
解:如图,将矩形ABCD以AD为轴翻折,将Rt△EFG 以EG 为轴翻折,则△B′C′H 即为未包裹住的面积,
∵Rt△HBE∽Rt△HB′C′,
∴????????????????′=????????????′????′,即10?????????′????????′=5?44,
解得HB′=8,
∴S△B′C′H=12·B′C′·B′H=12×4×8=16.
?
B
D
C(G)
A
B′
C′
F
E
H
课堂小结
利用解直角三角形解决实际问题的一般过程:
实际问题
数学问题
数学问题的答案
实际问题的答案
选用适当的锐角三角函数解直角三角形
对接中考
1.(2019·温州中考)某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆 AB 的长为( )
A. 95sin???? m B. 95cos???? m C. 59sin????? m D.59cos???? m
?
D
BD= 32+0.3=95
?
????????????????=????????????????
?
B
对接中考
2.(2020·长春中考)比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点B,塔身中心线AB与垂直中心线AC的夹角为∠A,过点B向垂直中心线AC引垂线,垂足为点D.通过测量可得AB、BD、AD的长度,利用测量所得的数据计算∠A的三角函数值,进而可求∠A的大小.下列关系式正确的是( )
sinA=???????????????? B.cosA=????????????????
C.tanA=????????????????? D. sinA=????????????????
?
解析:sinA=????????????????,cosA=?????????????????,tanA=?????????????????.
?
A
A
D
C
B
垂直中心线
塔身中心线
对接中考
3.(2020·孝感中考)某型号飞机的机翼形状如图所示,根据图中数据计算 AB 的长为 m.(结果保留根号)
解:如图,在Rt△DEA中,∵∠EDA=45°,
∴DE=AE=5?(m);
在Rt△BCF中,∵cos∠BCF=?????????????????,
∴CB=5cos30°?=1033?(m),∴BF=12?BC=533?(m),
∵AB+AE=EF+BF,
∴AB=3.4+533?5?=533?1.6(m).
?
F
E
533?1.6
?
D
5m
C
A
B
3.4m
45°
30°
课后作业
请完成课本后习题第2、7题.
