人教版数学九年级下册28章 锐角三角函数小结 课时1课件(20张)
文档属性
| 名称 | 人教版数学九年级下册28章 锐角三角函数小结 课时1课件(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 490.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 23:49:06 | ||
图片预览





文档简介
锐角三角函数
人教版-数学-九年级-下册
知识梳理-重点解析-深化练习
28 小结课
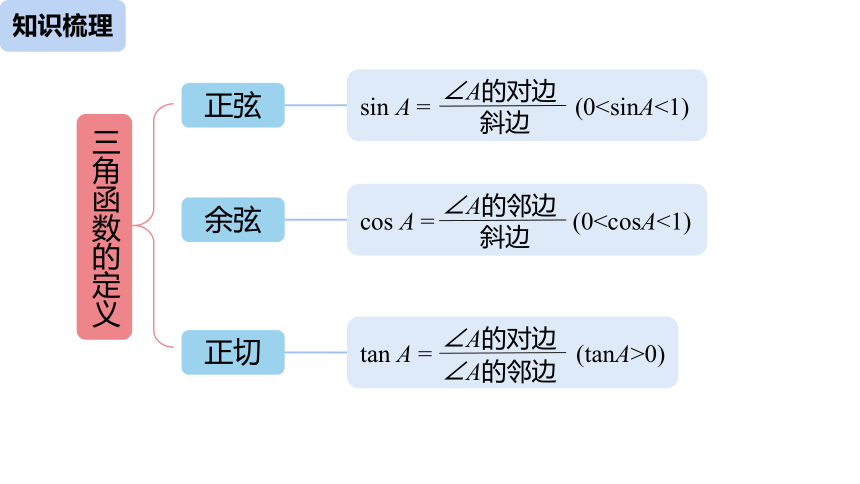
知识梳理
∠A的对边
斜边
sin A = (0三角函数的定义
正弦
∠A的邻边
斜边
cos A = (0余弦
∠A的对边
∠A的邻边
tan A = (tanA>0)
正切
知识梳理
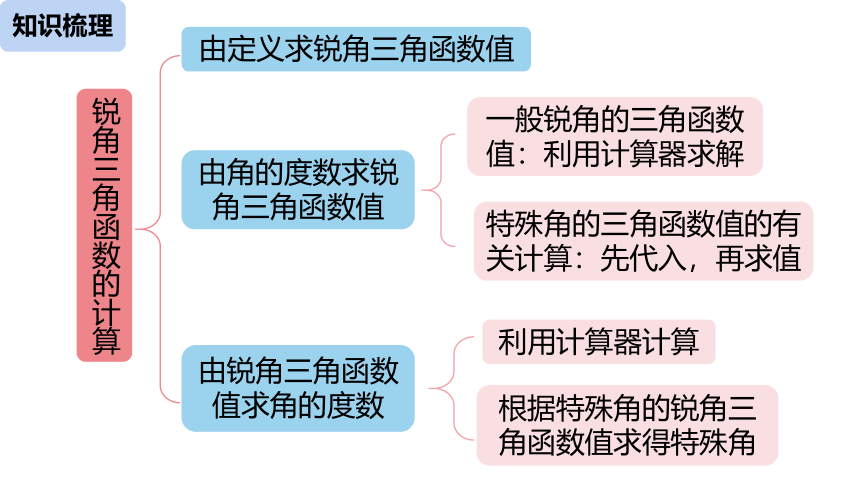
锐角三角函数的计算
由定义求锐角三角函数值
由锐角三角函数值求角的度数
由角的度数求锐角三角函数值
一般锐角的三角函数值:利用计算器求解
特殊角的三角函数值的有关计算:先代入,再求值
利用计算器计算
根据特殊角的锐角三角函数值求得特殊角
知识梳理
(1)∠A的正弦:sinA= = ;
(2)∠A的余弦:cosA= = ;
(3)∠A的正切:tanA= = .
1. 锐角三角函数
如图所示,在Rt△ABC中,∠C=90°,
a,b,c 分别是∠A,∠B,∠C 的对边.
∠A的邻边
斜边
∠A的邻边
∠A的对边
∠A的对边
斜边
知识梳理
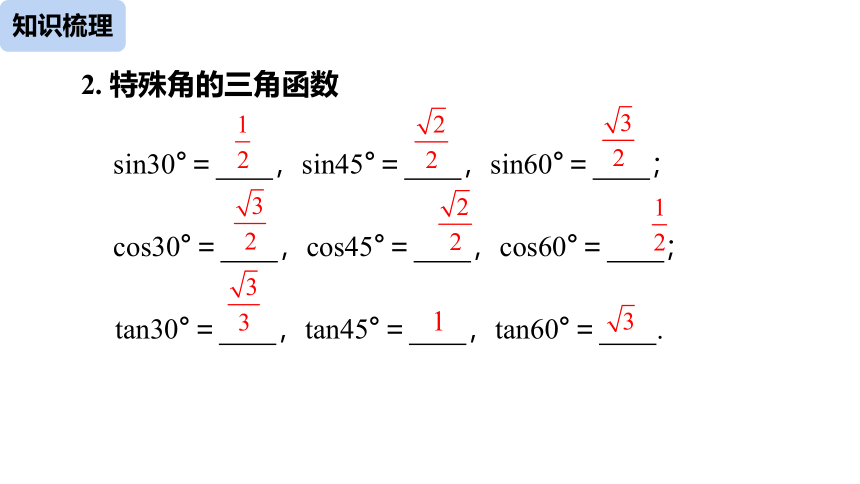
sin30°= ,sin45°= ,sin60°= ;
cos30°= ,cos45°= ,cos60°= ;
tan30°= ,tan45°= ,tan60°= .
2. 特殊角的三角函数
1
知识梳理
(1) 利用计算器求锐角三角函数值
屏幕显示结果.
第一步:按计算器 键,
sin
tan
cos
3. 借助计算器求锐角三角函数值及锐角
第二步:输入角度值,再按 键,
=
知识梳理
(2) 利用计算器求锐角的度数
还可以再按 键,进一步得到角的精确度数.
屏幕显示答案 .
° ' ″
2nd F
第一步:按计算器 键,
2nd F
sin
cos
tan
第二步:输入三角函数值,再按 键,
=
知识梳理
(1) 三角函数之间的关系
sinα = ,cosα = ,
sin2α + cos2α = ,tanα · tan(90°-α) = .
cos(90°-α)
sin(90°-α)
1
1
对于 sinα 与 tanα,角度越大,函数值越 ;
对于 cosα,角度越大,函数值越 .
大
小
(2) 锐角三角函数的增减性
4.探索三角函数的性质
重点解析
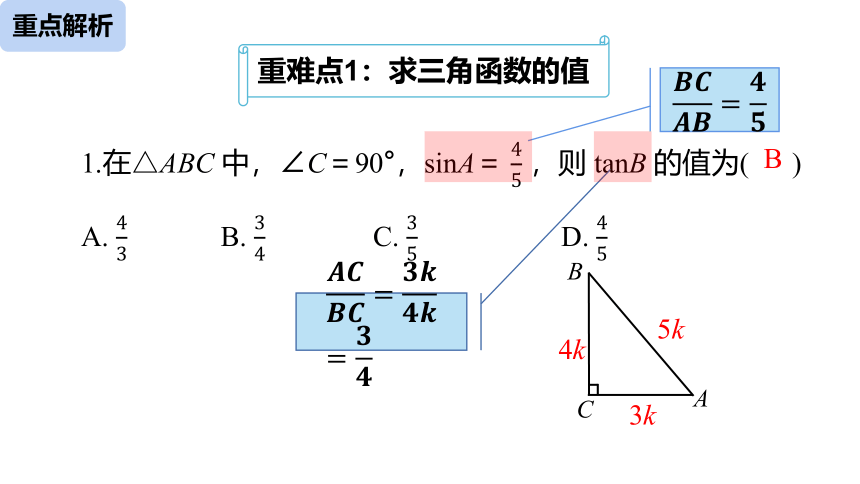
重难点1:求三角函数的值
1.在△ABC 中,∠C=90°,sinA= 45 ,则 tanB 的值为( )
A. 43 B. 34 C. 35 D. 45
?
B
A
B
C
4k
5k
3k
????????????????=????????
?
????????????????=????????????????=????????
?
重点解析
(1)根据特殊角的三角函数值求值;
(2)直接运用三角函数的定义求值;
(3)借助边的数量关系求值;
(4)借助等角求值;
(5)根据三角函数关系求值;
(6)构造直角三角形求值.
求三角函数值方法较多,解法灵活,在具体解题时要根据已知条件采取适当的计算方法,常用的方法主要有:
重点解析
2.矩形 ABCD 中 AB=10,BC=8,E 为 AD 边上一点,沿 CE 将△CDE 对折,使点 D 正好落在 AB 边上,求 tan∠AFE.
10
8
A
B
C
D
F
E
重点解析
解:由折叠的性质可得,CF=CD,
∠EFC=∠EDC=90°.
∵∠AFE+∠EFC+∠BFC=180°,
∴∠AFE+∠BFC=90°.
∵∠BCF+∠BFC=90°,∴∠AFE=∠BCF.
在Rt△BFC中,BC=8,CF=CD=10,
由勾股定理易得BF=6.
∴tan∠BCF = .
∴tan∠AFE=tan∠BCF= .
10
8
A
B
C
D
F
E
重点解析
重难点2:特殊角的三角函数值
计算:(1)
解:原式=
(2) 8sin260°+tan45°-4cos30°.
解:原式=
重点解析
重难点3:探索三角函数的性质
1.sin58°、cos58°、cos28°的大小关系是( )
A.cos28°<cos58°<sin58°
B.sin58°<cos28°<cos58°
C.cos58°<sin58°<cos28°
D.sin58°<cos58°<cos28°
cos32°
对于 cosα,角度越大,函数值越小
C
重点解析
2.在Rt△ABC中,∠C=90°,sinB=35,则sinA的值是( )
A. 35 B. 45 C. 53 D. 54
?
∠A与∠B互余
sin2A+sin2B=1
sinA=?????????????????=????????
?
B
深化练习
1. 在△ABC中, ∠A、 ∠B都是锐角,且sinA=cosB,那么△ABC一定是 ______ 三角形.
直角
∠A与∠B互余
深化练习
2. 如图,在网格中,小正方形的边长均为1,点A,B,C 都在格点上,则∠ABC 的正切值是____.
22
?
10
?
2
?
????????????????
?
深化练习
3.已知12<cosα<sin80°,则锐角α的取值范围是( )
A.30°<α<80°
B.10°<α<80°
C.60°<α<80°
D.10°<α<60°
?
cos60°
对于 cosα,角度越大,函数值越小
D
cos10°
深化练习
解:∵在 Rt△ABD中,tan∠BAD= ????????????????=34,
∴BD = AD·tan∠BAD=12× 34=9,
∴CD=BC-BD=14-9=5,
∴ ,
∴sinC= ????????????????=1213 .
?
4.如图,△ABC 中,AD⊥BC,垂足为点 D,若 BC=14,
AD=12,tan∠BAD= 34 ,求 sinC的值.
?
深化练习
(1) tan30°+cos45°+tan60°;
(2) tan30°· tan60°+ cos230°.
5.计算:
解:原式
解:原式
人教版-数学-九年级-下册
知识梳理-重点解析-深化练习
28 小结课
知识梳理
∠A的对边
斜边
sin A = (0
正弦
∠A的邻边
斜边
cos A = (0
∠A的对边
∠A的邻边
tan A = (tanA>0)
正切
知识梳理
锐角三角函数的计算
由定义求锐角三角函数值
由锐角三角函数值求角的度数
由角的度数求锐角三角函数值
一般锐角的三角函数值:利用计算器求解
特殊角的三角函数值的有关计算:先代入,再求值
利用计算器计算
根据特殊角的锐角三角函数值求得特殊角
知识梳理
(1)∠A的正弦:sinA= = ;
(2)∠A的余弦:cosA= = ;
(3)∠A的正切:tanA= = .
1. 锐角三角函数
如图所示,在Rt△ABC中,∠C=90°,
a,b,c 分别是∠A,∠B,∠C 的对边.
∠A的邻边
斜边
∠A的邻边
∠A的对边
∠A的对边
斜边
知识梳理
sin30°= ,sin45°= ,sin60°= ;
cos30°= ,cos45°= ,cos60°= ;
tan30°= ,tan45°= ,tan60°= .
2. 特殊角的三角函数
1
知识梳理
(1) 利用计算器求锐角三角函数值
屏幕显示结果.
第一步:按计算器 键,
sin
tan
cos
3. 借助计算器求锐角三角函数值及锐角
第二步:输入角度值,再按 键,
=
知识梳理
(2) 利用计算器求锐角的度数
还可以再按 键,进一步得到角的精确度数.
屏幕显示答案 .
° ' ″
2nd F
第一步:按计算器 键,
2nd F
sin
cos
tan
第二步:输入三角函数值,再按 键,
=
知识梳理
(1) 三角函数之间的关系
sinα = ,cosα = ,
sin2α + cos2α = ,tanα · tan(90°-α) = .
cos(90°-α)
sin(90°-α)
1
1
对于 sinα 与 tanα,角度越大,函数值越 ;
对于 cosα,角度越大,函数值越 .
大
小
(2) 锐角三角函数的增减性
4.探索三角函数的性质
重点解析
重难点1:求三角函数的值
1.在△ABC 中,∠C=90°,sinA= 45 ,则 tanB 的值为( )
A. 43 B. 34 C. 35 D. 45
?
B
A
B
C
4k
5k
3k
????????????????=????????
?
????????????????=????????????????=????????
?
重点解析
(1)根据特殊角的三角函数值求值;
(2)直接运用三角函数的定义求值;
(3)借助边的数量关系求值;
(4)借助等角求值;
(5)根据三角函数关系求值;
(6)构造直角三角形求值.
求三角函数值方法较多,解法灵活,在具体解题时要根据已知条件采取适当的计算方法,常用的方法主要有:
重点解析
2.矩形 ABCD 中 AB=10,BC=8,E 为 AD 边上一点,沿 CE 将△CDE 对折,使点 D 正好落在 AB 边上,求 tan∠AFE.
10
8
A
B
C
D
F
E
重点解析
解:由折叠的性质可得,CF=CD,
∠EFC=∠EDC=90°.
∵∠AFE+∠EFC+∠BFC=180°,
∴∠AFE+∠BFC=90°.
∵∠BCF+∠BFC=90°,∴∠AFE=∠BCF.
在Rt△BFC中,BC=8,CF=CD=10,
由勾股定理易得BF=6.
∴tan∠BCF = .
∴tan∠AFE=tan∠BCF= .
10
8
A
B
C
D
F
E
重点解析
重难点2:特殊角的三角函数值
计算:(1)
解:原式=
(2) 8sin260°+tan45°-4cos30°.
解:原式=
重点解析
重难点3:探索三角函数的性质
1.sin58°、cos58°、cos28°的大小关系是( )
A.cos28°<cos58°<sin58°
B.sin58°<cos28°<cos58°
C.cos58°<sin58°<cos28°
D.sin58°<cos58°<cos28°
cos32°
对于 cosα,角度越大,函数值越小
C
重点解析
2.在Rt△ABC中,∠C=90°,sinB=35,则sinA的值是( )
A. 35 B. 45 C. 53 D. 54
?
∠A与∠B互余
sin2A+sin2B=1
sinA=?????????????????=????????
?
B
深化练习
1. 在△ABC中, ∠A、 ∠B都是锐角,且sinA=cosB,那么△ABC一定是 ______ 三角形.
直角
∠A与∠B互余
深化练习
2. 如图,在网格中,小正方形的边长均为1,点A,B,C 都在格点上,则∠ABC 的正切值是____.
22
?
10
?
2
?
????????????????
?
深化练习
3.已知12<cosα<sin80°,则锐角α的取值范围是( )
A.30°<α<80°
B.10°<α<80°
C.60°<α<80°
D.10°<α<60°
?
cos60°
对于 cosα,角度越大,函数值越小
D
cos10°
深化练习
解:∵在 Rt△ABD中,tan∠BAD= ????????????????=34,
∴BD = AD·tan∠BAD=12× 34=9,
∴CD=BC-BD=14-9=5,
∴ ,
∴sinC= ????????????????=1213 .
?
4.如图,△ABC 中,AD⊥BC,垂足为点 D,若 BC=14,
AD=12,tan∠BAD= 34 ,求 sinC的值.
?
深化练习
(1) tan30°+cos45°+tan60°;
(2) tan30°· tan60°+ cos230°.
5.计算:
解:原式
解:原式
