人教版数学九年级下册28.2.2 应用举例 课时2课件(27张)
文档属性
| 名称 | 人教版数学九年级下册28.2.2 应用举例 课时2课件(27张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览





文档简介
28.2.2 应用举例
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
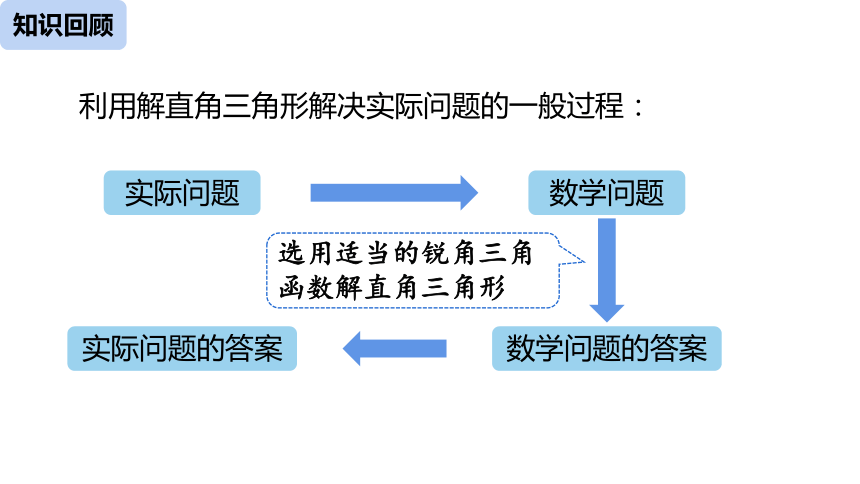
利用解直角三角形解决实际问题的一般过程:
实际问题
数学问题
数学问题的答案
实际问题的答案
选用适当的锐角三角函数解直角三角形
学习目标
2.能运用解直角三角形的知识解决有关仰角和俯角的实际问题,在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路.
1.巩固解直角三角形的有关知识.
课堂导入
某探险者某天到达如图所示的点 A 处时,他准备估算出自己离海拔 3500 m 的山峰顶点B处的水平距离.他能想出一个可行的办法吗?
.
A
B
.
.
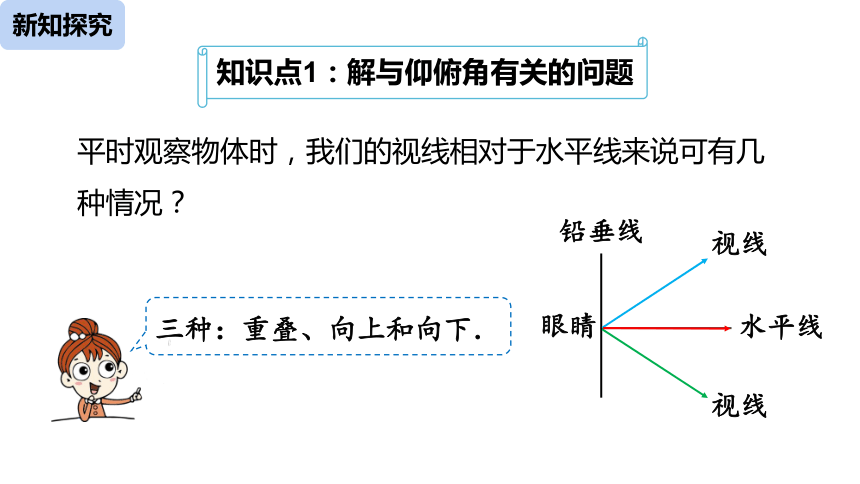
平时观察物体时,我们的视线相对于水平线来说可有几种情况?
三种:重叠、向上和向下.
新知探究
知识点1:解与仰俯角有关的问题
铅垂线
眼睛
视线
水平线
视线
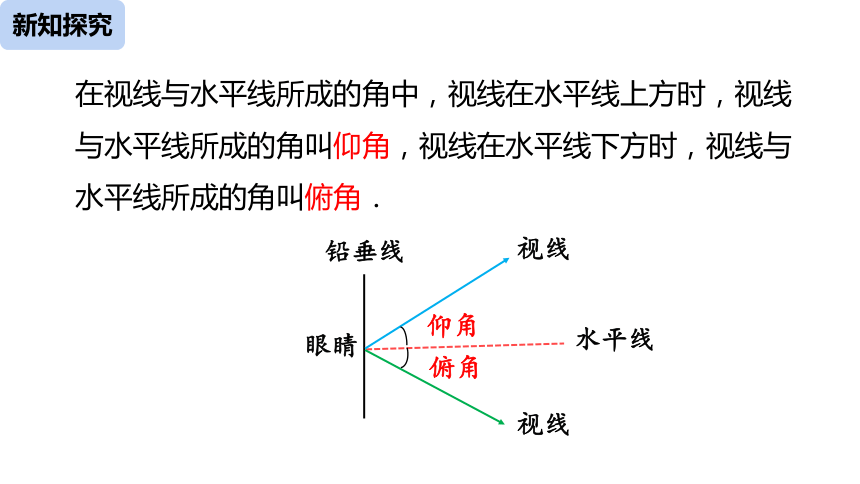
在视线与水平线所成的角中,视线在水平线上方时,视线与水平线所成的角叫仰角,视线在水平线下方时,视线与水平线所成的角叫俯角.
新知探究
铅垂线
眼睛
视线
水平线
视线
仰角
俯角
新知探究
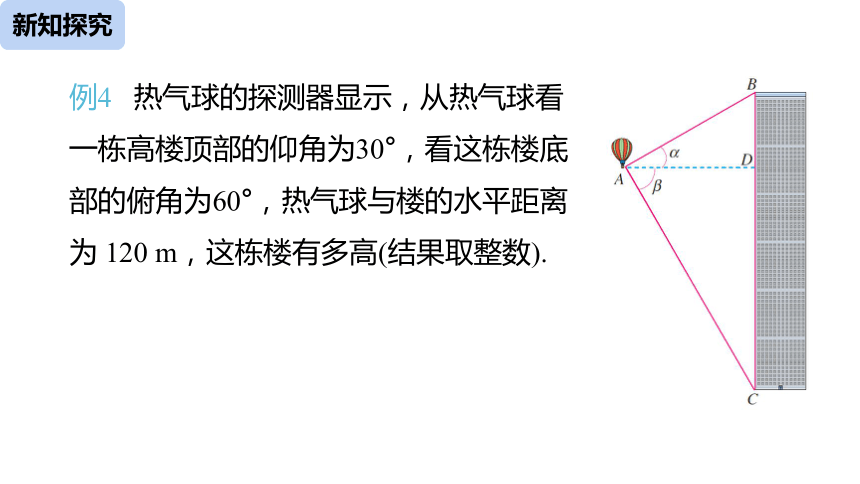
例4 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为 120 m,这栋楼有多高(结果取整数).
新知探究
分析:我们知道,在视线与水平线所成的角中,视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α =30°,β =60°. 在Rt△ABD中,α =30°,AD=120,所以可以利用解直角三角形的知识求出 BD ;类似地可以求出 CD ,进而求出 BC .
新知探究
解:如图,α = 30°,β= 60°, AD=120.
答:这栋楼高约为277m.
新知探究
如图,小明想测量塔 AB 的高度.他在 D 处仰望塔顶,测得仰角为 30°,再往塔的方向前进 50 m 至 C 处,测得仰角为60°,已知小明的身高为 1.5 m,那么该塔有多高?(结果取整数)
D′
A
B′
B
D
C′
C
新知探究
解:如图,由题意可知,∠AD′B′=30°,∠AC′B′=60°,
DC= 50 m.
∴ ∠D′AB′=60°,∠C′AB′=30°,D′C′=50 m .设 AB′=x m.
D′
A
B′
B
D
C′
C
跟踪训练
如图,在数学活动课中,小敏为了测量校园内旗杆 CD 的高度,先在教学楼的底端 A 处,观测到旗杆顶端 C 的仰角∠CAD =60°,然后爬到教学楼上的 B 处,观测
到旗杆底端 D的俯角是30°,已知教学楼 AB 高4米.
(1)求教学楼与旗杆的水平距离 AD (结果
保留根号);
(2)求旗杆 CD 的高度.
(1)求教学楼与旗杆的水平距离 AD (结果保留根号);
解:(1)∵在教学楼上的 B 处观测到旗杆底端 D 的俯角是30°,∴∠ADB =30°.
在Rt△ABD 中,∵∠BAD =90°,∠ADB =30°,AB =4米,
∴ AD =????????tan∠????????????=4tan30°=433=43(米).
∴教学楼与旗杆的水平距离 AD 为43 米.
?
跟踪训练
(2)求旗杆 CD 的高度.
解:(2)在 Rt△ACD 中,∵∠ADC =90°,∠CAD =60°,AD =43米,
∴ CD =AD·tan60°=43?×3=12(米).
∴ 旗杆 CD 的高度是12米.
?
跟踪训练
随堂练习
1.如图,某同学在楼房的 A 处测得荷塘一端 B 处的俯角为24°,荷塘另一端点 D 与点 C,B 在同一直线上,已知楼房 AC=32米,CD=16米,则荷塘的宽 BD 为( )(sin24°≈0.41,cos24°≈0.91,tan24°≈0.45.结果精确到0.1)
A.55.1?米 B.30.4?米
C.51.2?米 D.19.2?米
随堂练习
解:由题意知,∠ABC=24°,∠ACB=90°,AC=32米,
∵tan∠ABC=tan24°=????????????????,
∴BC=????????tan24°=320.45≈71.1米,
∵CD=16米,
∴BD=BC-CD=71.1-16=55.1米.
?
随堂练习
2.如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;
(2)量得测角仪的高度CD=a;
(3)量得测角仪到旗杆的水平距离DB=b.
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
( )
A.a+btanαB.a+bsinα
C.a+????tan????D.a+????sin????
?
α
随堂练习
解析:如图,过C作CF⊥AB于点F,则四边形BFCD是矩形,
∴BF=CD=a,CF=DB =b,
∵∠ACF=α,
∴tanα=????????????????=????????????????,
∴AF=btanα,
∴AB=AF+BF=a+btanα.
?
F
α
随堂练习
3.如图,为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB的高度等于( )
A. 12(3+1) m
B. 12(3?1) m
C. 6(3+1) m
D. 6(3?1) m
?
A
B
C
D
随堂练习
解:∵在Rt△ABC中,∠ACB=30°,
∴tan∠ACB=tan30°=????????????????,
∴BC=????????tan30°=3AB,
∵在Rt△ABD中,tan∠ADB=tan45°=????????????????,
∴BD=????????tan45°=AB.
∵CD=BC-BD=AB(3-1)=12,
∴AB=6(3?+1)m.
?
A
B
C
D
课堂小结
仰角、俯角的概念
运用解直角三角形解决仰角、俯角问题
利用仰角、俯角解直角三角形
测量高度
测量距离
对接中考
1.(2020·长沙中考)从一艘船上测得到海岸上高为42米的灯塔顶部的仰角为30°,则船离灯塔的水平距离是( )
A.423米 B.143米
C.21米 D.42米
?
30°
42米
42÷tan30°=423
?
A
对接中考
2.(2019·广东中考)如图,某校教学楼 AC 与实验楼 BD 的水平间距 CD = 153 米,在实验楼顶部 B 点测得教学楼顶部 A 点的仰角是 30°,底部 C 点的俯角是 45°,则教学楼 AC 的高度是米(结果保留根号).
?
对接中考
解析:设过点 B 的水平线与 AC 交于点 E,如图所示.
易知在Rt△BEC 中,∠CBE =45°,BE = CD =153 米,
所以 CE =BE×tan45°=153 米.
在Rt△ABE 中,∠ABE =30°,BE = 153 米,
所以 AE = BE×tan30°=15米.
所以 AC =CE +AE =(153?+15)米.
?
E
对接中考
3.(2020·眉山中考)某数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为 20 米的发射塔 AB,如图所示.在山脚平地上的 D 处测得塔底 B 的仰角为 30°,向小山前进 80 米到达点 E 处,测得塔顶 A 的仰角为60°,求小山 BC 的高度.
对接中考
解:设BC为x米,则AC=(20+x)米,
由条件知∠DBC=∠AEC=60°,DE=80米.
在Rt△DBC中,tan60°=????????????????=?????????????,则DC=3x米.
∴CE=(3x-80) 米.
在Rt△ACE中,tan60°=?????????????????=20+????3?????80?=3.
解得x=10+403?.
答:小山BC的高度为(10+403)米.
?
课后作业
请完成课本后习题第3、4题.
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
利用解直角三角形解决实际问题的一般过程:
实际问题
数学问题
数学问题的答案
实际问题的答案
选用适当的锐角三角函数解直角三角形
学习目标
2.能运用解直角三角形的知识解决有关仰角和俯角的实际问题,在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路.
1.巩固解直角三角形的有关知识.
课堂导入
某探险者某天到达如图所示的点 A 处时,他准备估算出自己离海拔 3500 m 的山峰顶点B处的水平距离.他能想出一个可行的办法吗?
.
A
B
.
.
平时观察物体时,我们的视线相对于水平线来说可有几种情况?
三种:重叠、向上和向下.
新知探究
知识点1:解与仰俯角有关的问题
铅垂线
眼睛
视线
水平线
视线
在视线与水平线所成的角中,视线在水平线上方时,视线与水平线所成的角叫仰角,视线在水平线下方时,视线与水平线所成的角叫俯角.
新知探究
铅垂线
眼睛
视线
水平线
视线
仰角
俯角
新知探究
例4 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为 120 m,这栋楼有多高(结果取整数).
新知探究
分析:我们知道,在视线与水平线所成的角中,视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α =30°,β =60°. 在Rt△ABD中,α =30°,AD=120,所以可以利用解直角三角形的知识求出 BD ;类似地可以求出 CD ,进而求出 BC .
新知探究
解:如图,α = 30°,β= 60°, AD=120.
答:这栋楼高约为277m.
新知探究
如图,小明想测量塔 AB 的高度.他在 D 处仰望塔顶,测得仰角为 30°,再往塔的方向前进 50 m 至 C 处,测得仰角为60°,已知小明的身高为 1.5 m,那么该塔有多高?(结果取整数)
D′
A
B′
B
D
C′
C
新知探究
解:如图,由题意可知,∠AD′B′=30°,∠AC′B′=60°,
DC= 50 m.
∴ ∠D′AB′=60°,∠C′AB′=30°,D′C′=50 m .设 AB′=x m.
D′
A
B′
B
D
C′
C
跟踪训练
如图,在数学活动课中,小敏为了测量校园内旗杆 CD 的高度,先在教学楼的底端 A 处,观测到旗杆顶端 C 的仰角∠CAD =60°,然后爬到教学楼上的 B 处,观测
到旗杆底端 D的俯角是30°,已知教学楼 AB 高4米.
(1)求教学楼与旗杆的水平距离 AD (结果
保留根号);
(2)求旗杆 CD 的高度.
(1)求教学楼与旗杆的水平距离 AD (结果保留根号);
解:(1)∵在教学楼上的 B 处观测到旗杆底端 D 的俯角是30°,∴∠ADB =30°.
在Rt△ABD 中,∵∠BAD =90°,∠ADB =30°,AB =4米,
∴ AD =????????tan∠????????????=4tan30°=433=43(米).
∴教学楼与旗杆的水平距离 AD 为43 米.
?
跟踪训练
(2)求旗杆 CD 的高度.
解:(2)在 Rt△ACD 中,∵∠ADC =90°,∠CAD =60°,AD =43米,
∴ CD =AD·tan60°=43?×3=12(米).
∴ 旗杆 CD 的高度是12米.
?
跟踪训练
随堂练习
1.如图,某同学在楼房的 A 处测得荷塘一端 B 处的俯角为24°,荷塘另一端点 D 与点 C,B 在同一直线上,已知楼房 AC=32米,CD=16米,则荷塘的宽 BD 为( )(sin24°≈0.41,cos24°≈0.91,tan24°≈0.45.结果精确到0.1)
A.55.1?米 B.30.4?米
C.51.2?米 D.19.2?米
随堂练习
解:由题意知,∠ABC=24°,∠ACB=90°,AC=32米,
∵tan∠ABC=tan24°=????????????????,
∴BC=????????tan24°=320.45≈71.1米,
∵CD=16米,
∴BD=BC-CD=71.1-16=55.1米.
?
随堂练习
2.如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;
(2)量得测角仪的高度CD=a;
(3)量得测角仪到旗杆的水平距离DB=b.
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
( )
A.a+btanαB.a+bsinα
C.a+????tan????D.a+????sin????
?
α
随堂练习
解析:如图,过C作CF⊥AB于点F,则四边形BFCD是矩形,
∴BF=CD=a,CF=DB =b,
∵∠ACF=α,
∴tanα=????????????????=????????????????,
∴AF=btanα,
∴AB=AF+BF=a+btanα.
?
F
α
随堂练习
3.如图,为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB的高度等于( )
A. 12(3+1) m
B. 12(3?1) m
C. 6(3+1) m
D. 6(3?1) m
?
A
B
C
D
随堂练习
解:∵在Rt△ABC中,∠ACB=30°,
∴tan∠ACB=tan30°=????????????????,
∴BC=????????tan30°=3AB,
∵在Rt△ABD中,tan∠ADB=tan45°=????????????????,
∴BD=????????tan45°=AB.
∵CD=BC-BD=AB(3-1)=12,
∴AB=6(3?+1)m.
?
A
B
C
D
课堂小结
仰角、俯角的概念
运用解直角三角形解决仰角、俯角问题
利用仰角、俯角解直角三角形
测量高度
测量距离
对接中考
1.(2020·长沙中考)从一艘船上测得到海岸上高为42米的灯塔顶部的仰角为30°,则船离灯塔的水平距离是( )
A.423米 B.143米
C.21米 D.42米
?
30°
42米
42÷tan30°=423
?
A
对接中考
2.(2019·广东中考)如图,某校教学楼 AC 与实验楼 BD 的水平间距 CD = 153 米,在实验楼顶部 B 点测得教学楼顶部 A 点的仰角是 30°,底部 C 点的俯角是 45°,则教学楼 AC 的高度是米(结果保留根号).
?
对接中考
解析:设过点 B 的水平线与 AC 交于点 E,如图所示.
易知在Rt△BEC 中,∠CBE =45°,BE = CD =153 米,
所以 CE =BE×tan45°=153 米.
在Rt△ABE 中,∠ABE =30°,BE = 153 米,
所以 AE = BE×tan30°=15米.
所以 AC =CE +AE =(153?+15)米.
?
E
对接中考
3.(2020·眉山中考)某数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为 20 米的发射塔 AB,如图所示.在山脚平地上的 D 处测得塔底 B 的仰角为 30°,向小山前进 80 米到达点 E 处,测得塔顶 A 的仰角为60°,求小山 BC 的高度.
对接中考
解:设BC为x米,则AC=(20+x)米,
由条件知∠DBC=∠AEC=60°,DE=80米.
在Rt△DBC中,tan60°=????????????????=?????????????,则DC=3x米.
∴CE=(3x-80) 米.
在Rt△ACE中,tan60°=?????????????????=20+????3?????80?=3.
解得x=10+403?.
答:小山BC的高度为(10+403)米.
?
课后作业
请完成课本后习题第3、4题.
