人教版数学九年级下册28.2.2 应用举例 课时3课件(38张)
文档属性
| 名称 | 人教版数学九年级下册28.2.2 应用举例 课时3课件(38张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 23:50:08 | ||
图片预览








文档简介
28.2.2 应用举例
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
西南
东北
东
西
北
南
西北
东南
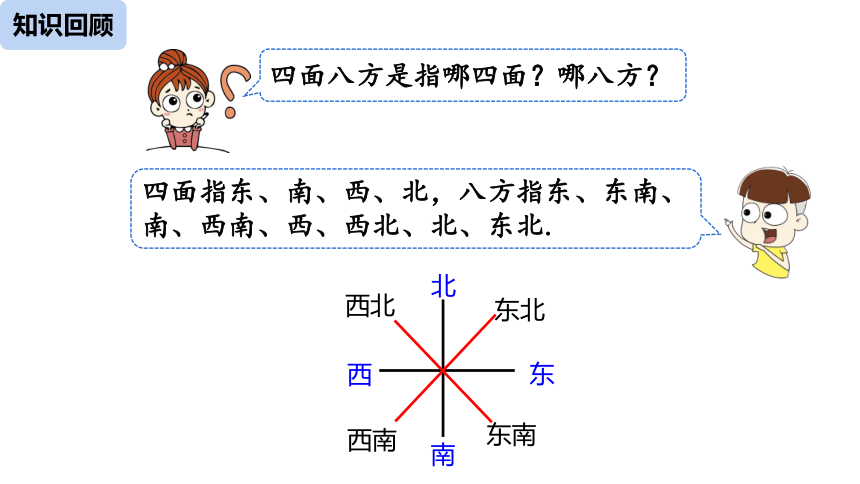
四面八方是指哪四面?哪八方?
四面指东、南、西、北,八方指东、东南、南、西南、西、西北、北、东北.
学习目标
1.正确理解方向角、坡度的概念.
2.能运用解直角三角形知识解决方向角、坡度的问题;能够掌握综合性较强的题型,融会贯通地运用相关的数学知识,进一步提高运用解直角三角形知识分析解决问题的综合能力.
课堂导入
方向角在测绘、地质与地球物理勘探、航空、航海、炮兵射击及部队行进时等都广泛使用. 你知道怎样利用方向角测量两地的距离吗?
新知探究
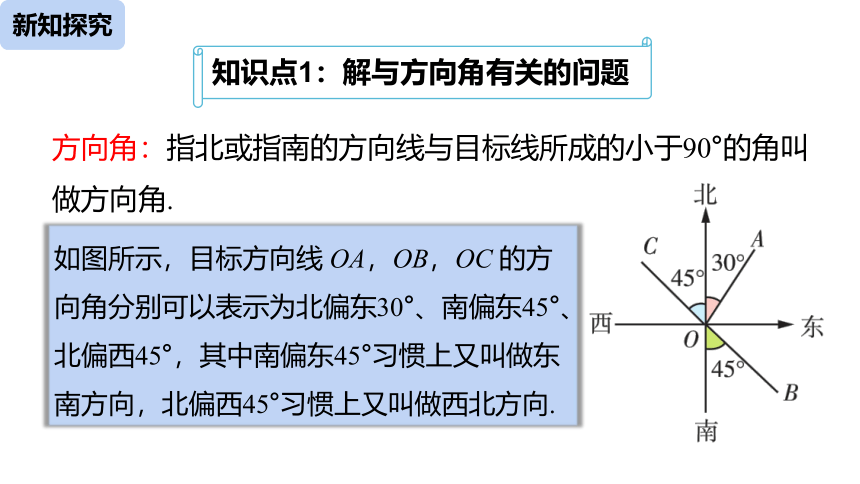
方向角:指北或指南的方向线与目标线所成的小于90°的角叫做方向角.
知识点1:解与方向角有关的问题
如图所示,目标方向线 OA,OB,OC 的方向角分别可以表示为北偏东30°、南偏东45°、北偏西45°,其中南偏东45°习惯上又叫做东南方向,北偏西45°习惯上又叫做西北方向.
新知探究
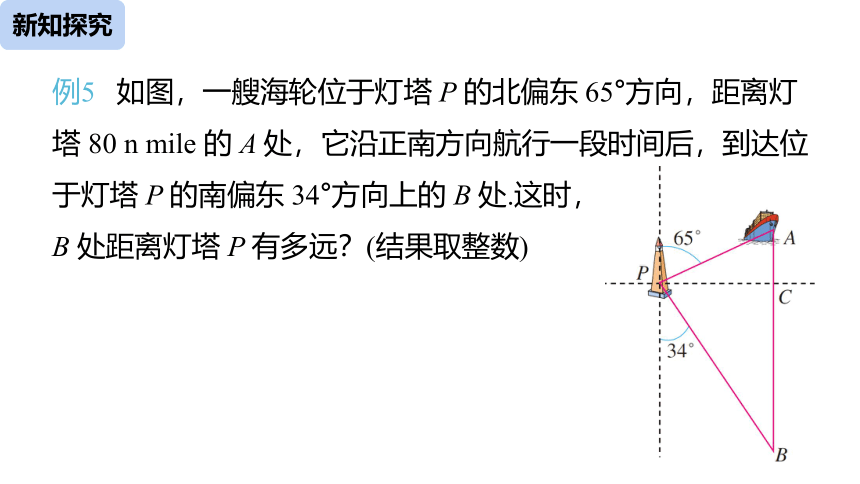
例5 如图,一艘海轮位于灯塔 P 的北偏东 65°方向,距离灯塔 80 n mile 的 A 处,它沿正南方向航行一段时间后,到达位于灯塔 P 的南偏东 34°方向上的 B 处.这时,
B 处距离灯塔 P 有多远?(结果取整数)
新知探究
解:如图 ,在 Rt△APC 中,
PC =PA·cos(90°-65°) =80×cos25° ≈ 72.505(n mile).
在 Rt△BPC 中,∠B=34°,
因此,当海轮到达位于灯塔 P 的南偏东34°方向时,它距离灯塔 P 大约130 n mile.
新知探究
1.解决实际问题时,可利用正南、正北、正东、正西方向线构造直角三角形.
2.方向角通常以南北方向线为主,分南偏东(或西)和北偏东(或西),观测点不同,所得的方向角也不同,但各个观测点的南北方向线是互相平行的.
新知探究
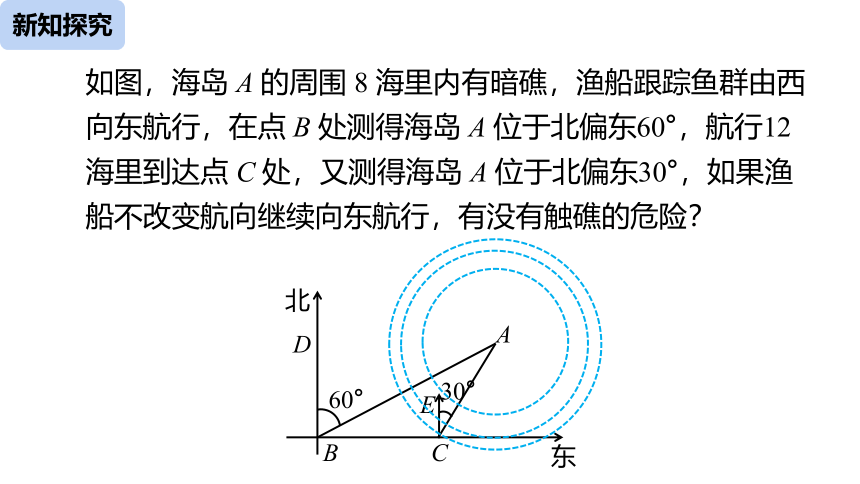
如图,海岛 A 的周围 8 海里内有暗礁,渔船跟踪鱼群由西向东航行,在点 B 处测得海岛 A 位于北偏东60°,航行12海里到达点 C 处,又测得海岛 A 位于北偏东30°,如果渔船不改变航向继续向东航行,有没有触礁的危险?
北
东
A
C
B
60°
30°
D
E
新知探究
解:过 A 作AF⊥BC的延长线于点 F,则 AF 是点 A 到 BC 的 最短距离.
∵BD//CE//AF,
∴∠DBA =∠BAF =60°,∠ACE =∠CAF =30°,
∴∠BAC =∠BAF-∠CAF =60°-30°=30°.
又∵∠ABC =∠DBF-∠DBA = 90°-60°=30°=∠BAC,
∴ BC =AC =12海里,
∴AF =AC·cos30°=63 (海里),
63 ≈10.392>8,
故没有触礁的危险.
?
北
东
A
C
B
60°
30°
D
E
F
新知探究
解决暗礁影响类问题的方法
求解是否触礁的问题时,一般都是求出暗礁中心到航线的距离,将这个距离与暗礁半径比较大小,距离小于或等于半径有危险,距离大于半径没有危险.台风、噪声影响等其他类似问题也用类似方法解决.
跟踪训练
如图,一轮船在 M 处观测灯塔 P 位于南偏西30°方向,该轮船沿正南方向以 15 海里/时的速度匀速航行 2 小时后到达 N 处,再观测灯塔 P 位于南偏西 60° 方向,若该轮船继续向南航行至灯塔 P 最近的位置 T 处,此时轮船与灯塔之间的距离 PT 为 海里(结果保留根号).
解析:由题意得,MN =15×2=30(海里).
∵ ∠PMN =30° ,∠PNT = 60°,
∴ ∠MPN =∠PMN = 30°,
∴ PN =MN =30 海里.
∵ 该轮船继续向南航行至 T 处距灯塔 P 最近,
∴ PT⊥MT,
∴ PT =PN·sin∠PNT=153海里.
?
跟踪训练
新知探究
知识点2:解与坡度有关的问题
如图,从山脚到山顶有两条路 AB 与 BC,问哪条路比较陡?
A
B
C
如何用数量来表示哪条路陡呢?
新知探究
坡面与水平面的夹角叫做坡角,一般用字母 α,β,γ 表示 .
坡面的铅直高度 ( h ) 和水平宽度 ( l ) 的比叫做坡面的坡度 (或坡比),通常用 i 表示, 即 i = h : l .
α
l
h
i= h : l
坡面
水平面
1.坡度不是角的度数,它是坡角的正切值,即 i =tanα;
2.坡度越大,坡角 α 就越大,坡面就越陡.
新知探究
1.如图,一山坡的坡度为 i=1:2.小刚从山脚 A 出发, 沿山坡向上走了 240 m 到达点 C.这座山坡的坡角约是多少度?小刚上升了约多少米?(角度精确到 0.01°,长度精确到0.1 m)
i=1:2
A
B
C
新知探究
在 Rt△ABC 中,∠B =90°,∠A =26.57°,AC =240 m,
解:
用 α 表示坡角的大小,由题意可得
因此 α≈26.57°.
即这座山坡的坡角约为 26.57°,小刚上升了约 107.3 m.
从而 BC =240×sin26.57°≈107.3(m).
因此
i=1:2
A
B
C
α
新知探究
2.水库大坝的横断面是梯形,坝顶宽 6 m,坝高 23 m,斜坡 AB 的坡度 i1=1∶3,斜坡 CD 的坡度 i2=1∶2.5,求:
(1) 斜坡 CD 的坡角 α (精确到 1°);
A
D
B
C
i2=1:2.5
23
6
α
i1=1:3
解: 斜坡 CD 的坡度 i2= tanα = 1 : 2.5=0.4,
由计算器可算得 α ≈ 22°.
故斜坡 CD 的坡角 α 约为 22°.
新知探究
解:分别过点 B、C 作 BE⊥AD,CF⊥AD,垂足分别
为点 E、 F,由题意可知 BE=CF=23 m , EF=BC=6 m.
(2) 坝底 AD 与斜坡 AB 的长度 (精确到 0.1 m).
E
F
A
D
B
C
23
6
α
i1=1:3
i2=1:2.5
在 Rt△ABE 中,
1
新知探究
=69+6+57.5=132.5 (m).
在 Rt△ABE 中,由勾股定理可得
故坝底 AD 的长度为 132.5 m,斜坡 AB 的长度约为 72.7 m.
E
F
A
D
B
C
i2=1:2.5
23
6
α
i1=1:3
在 Rt△DCF 中,同理可得
2
如图所示,某拦水大坝的横断面为梯形 ABCD,AE,DF 为梯形的高,其中迎水坡 AB 的坡角 α =45°,坡长 AB =62 米,背水坡 CD 的坡度 i=1:3( i 为 DF 与 FC 的比值),则背水坡 CD 的坡长为米.
?
跟踪训练
解析:迎水坡 AB 的坡角 α=45°,坡长 AB =62米,
∴ AE =AB·sinα=62?×sin45°=6(米).
∵ 背水坡 CD 的坡度 i=1: 3( i 为 DF 与 FC 的比值),
∴ tanC =13=33,
∴ ∠C =30°,
∴ CD =2DF =2AE =12米.
?
跟踪训练
随堂练习
1.如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AP=63千米,则A,B两点间的距离为( )千米.
A.4 B.43 C.2 D.6
?
随堂练习
解析:由题意知,∠PAB=30°,∠PBC=60°,
∴∠APB=∠PBC-∠PAB=60°-30°=30°,
∴∠PAB=∠APB,∴AB=PB,
在Rt△PAC中,∵AP=63千米,
∴PC=12PA=33千米,
在Rt△PBC中,∵sin∠PBC=????????????????,
∴PB=????????sin60°?=3332?=6千米.
?
随堂练习
2.为满足广大滑板爱好者的需求,某广场修建了一个小型滑板场,如图,爱好者们从 A 处滑下,经缓冲区 EF 之后,滑向 C 处,已知 AB⊥BD 于点 B,CD⊥BD 于点 D,AB =2CD,BD = 13 m,缓冲区EF =3 m,斜坡轨道 AE 的坡度 i =1:2,斜坡轨道 FC 的坡角为 37°,其中 B、E、F、D 在同一直线上,则 AB 的长度约为( )
(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
A.3.55 m B.3.75 m
C.3.95 m D.4.15 m
A
D
C
B
E
F
随堂练习
解析:∵AB=2CD,∴设CD=x,则AB=2x,
∵tan37°≈0.75,
∴????????????????=?????????????=0.75,则DF=43x,
∵斜坡轨道AE的坡度i=1:2,
∴BE=2AB=4x,
故BD-EF=BE+FD=13-3=4x+43x,
解得x=158,故AB=2× 158?=154?=3.75(m).
?
A
D
C
B
E
F
随堂练习
3.为了维护海洋权益,国家海洋局加大了在南海的巡逻力度,一天,我国两艘海监船刚好在我国某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60(6+2)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(6?2)海里.
?
随堂练习
(1)分别求出 A 与 C 及 B 与 C 的距离 AC、BC;(结果保留根号)
解:(1)如图,过点 C 作 CE⊥AB 于点 E,
可得∠ACE =30°,∠BCE =45°,
设 AE =x 海里,
则在 Rt△ACE 中,CE =3x 海里,AC =2x 海里,
在 Rt△BCE 中,BE =CE =3x 海里,BC =6x 海里.
∵ AB =AE +BE,∴ x+3x=60(6+2),
解得 x =602.
∴ AC =1202 海里,BC = 1203 海里.
?
E
随堂练习
(2)已知在灯塔D周围100海里范围内有暗礁群,我国 A处海监船沿AC前往C处盘查,途中有无触礁的危险?
(参考数据:2≈1.41,3≈1.73,6≈2.45)
?
解:(2)如图,过点 D 作 DF⊥AC 于点 F,
则∠DAF =60°.
在Rt△AFD 中,DF =DA·sin 60°=32DA,
∴ DF =32?×120( 6?2 )=60( 32?6)≈106.8(海里)> 100 海里,
∴ 无触礁危险.
?
F
课堂小结
解直角三角形的应用
方向角问题
坡度问题
坡角
坡度(或坡比):
1.(2019·长沙中考)如图,一艘轮船从位于灯塔 C 的北偏东 60°方向,距离灯塔 60 n mile 的小岛 A 出发,沿正南方向航行一段时间后,到达位于灯塔 C 的南偏东 45°方向上的 B 处,这时轮船 B 与小岛 A 的距离是( )
A.303 n mile
B.60 n mile
C.120 n mile
D. (30+303) n mile
?
对接中考
对接中考
解析:如图,设过点 C 的水平线与 AB 交于点 D.
由题意易知,∠ACD =30°,∠BCD =45°,AC =60 n mile.
在 Rt△ACD 中,sin∠ACD =????????????????,cos∠ACD =?????????????????,
∴AD =AC·sin∠ACD =30 n mile,
CD =AC·cos∠ACD = 60×32=303(n mile).
在 Rt△DCB 中,易知∠B =∠BCD =45°,
∴ BD =CD =303 n mile,
∴ AB =AD+BD =(30+303)n mile.
?
对接中考
2.(2020·仙桃市中考)如图,海中有个小岛 A,一艘轮船由西向东航行,在点 B 处测得小岛 A 位于它的东北方向,此时轮船与小岛相距 20 海里,继续航行至点 D 处,测得小岛 A 在它的北偏西60°方向,此时轮船与小岛的距离 AD 为 海里.
A
B
D
北
东
45°
60°
对接中考
解:如图,过点A作AC⊥BD于点C,
根据题意可知:
∠BAC=∠ABC=45°,∠ADC=30°,AB=20,
在Rt△ABC中,AC=BC=AB·sin45°=20×22=102,
在Rt△ACD中,∠ADC=30°,
∴AD=2AC=202(海里).
?
C
A
B
D
北
东
45°
60°
对接中考
3.(2020·泰安中考)如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC//AD,BE⊥AD,斜坡 AB 长 26 m,斜坡 AB 的坡比为 12:5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过 50°时,可确保山体不滑坡.如果改造时保持
坡脚 A 不动,则坡顶 B 沿 BC 至少向右移
m时,才能确保山体不滑坡.
(取tan50°=1.2)
A
E
D
C
B
对接中考
解:在BC上取点F,使∠FAE=50°,过点F作FH⊥AD于点 H,
∵BF//EH,BE⊥AD,FH⊥AD,
∴四边形BEHF为矩形,
∴BF=EH,BE=FH,
∵斜坡AB的坡比为12:5,
∴????????????????=125,
?
F
H
A
E
D
C
B
对接中考
设BE=12x,则AE=5x,
由勾股定理得,AE2+BE2=AB2,即(5x)2+(12x)2=262,
解得x=2,
∴AE=10,BE=24,∴FH=BE=24,
在Rt△FAH中,tan∠FAH=????????????????,
∴AH=????????tan50°=20,∴BF=EH=AH-AE=10,
∴至少向右移10m时,才能确保山体不滑坡.
?
F
H
A
E
D
C
B
课后作业
请完成课本后习题第5、9题.
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
西南
东北
东
西
北
南
西北
东南
四面八方是指哪四面?哪八方?
四面指东、南、西、北,八方指东、东南、南、西南、西、西北、北、东北.
学习目标
1.正确理解方向角、坡度的概念.
2.能运用解直角三角形知识解决方向角、坡度的问题;能够掌握综合性较强的题型,融会贯通地运用相关的数学知识,进一步提高运用解直角三角形知识分析解决问题的综合能力.
课堂导入
方向角在测绘、地质与地球物理勘探、航空、航海、炮兵射击及部队行进时等都广泛使用. 你知道怎样利用方向角测量两地的距离吗?
新知探究
方向角:指北或指南的方向线与目标线所成的小于90°的角叫做方向角.
知识点1:解与方向角有关的问题
如图所示,目标方向线 OA,OB,OC 的方向角分别可以表示为北偏东30°、南偏东45°、北偏西45°,其中南偏东45°习惯上又叫做东南方向,北偏西45°习惯上又叫做西北方向.
新知探究
例5 如图,一艘海轮位于灯塔 P 的北偏东 65°方向,距离灯塔 80 n mile 的 A 处,它沿正南方向航行一段时间后,到达位于灯塔 P 的南偏东 34°方向上的 B 处.这时,
B 处距离灯塔 P 有多远?(结果取整数)
新知探究
解:如图 ,在 Rt△APC 中,
PC =PA·cos(90°-65°) =80×cos25° ≈ 72.505(n mile).
在 Rt△BPC 中,∠B=34°,
因此,当海轮到达位于灯塔 P 的南偏东34°方向时,它距离灯塔 P 大约130 n mile.
新知探究
1.解决实际问题时,可利用正南、正北、正东、正西方向线构造直角三角形.
2.方向角通常以南北方向线为主,分南偏东(或西)和北偏东(或西),观测点不同,所得的方向角也不同,但各个观测点的南北方向线是互相平行的.
新知探究
如图,海岛 A 的周围 8 海里内有暗礁,渔船跟踪鱼群由西向东航行,在点 B 处测得海岛 A 位于北偏东60°,航行12海里到达点 C 处,又测得海岛 A 位于北偏东30°,如果渔船不改变航向继续向东航行,有没有触礁的危险?
北
东
A
C
B
60°
30°
D
E
新知探究
解:过 A 作AF⊥BC的延长线于点 F,则 AF 是点 A 到 BC 的 最短距离.
∵BD//CE//AF,
∴∠DBA =∠BAF =60°,∠ACE =∠CAF =30°,
∴∠BAC =∠BAF-∠CAF =60°-30°=30°.
又∵∠ABC =∠DBF-∠DBA = 90°-60°=30°=∠BAC,
∴ BC =AC =12海里,
∴AF =AC·cos30°=63 (海里),
63 ≈10.392>8,
故没有触礁的危险.
?
北
东
A
C
B
60°
30°
D
E
F
新知探究
解决暗礁影响类问题的方法
求解是否触礁的问题时,一般都是求出暗礁中心到航线的距离,将这个距离与暗礁半径比较大小,距离小于或等于半径有危险,距离大于半径没有危险.台风、噪声影响等其他类似问题也用类似方法解决.
跟踪训练
如图,一轮船在 M 处观测灯塔 P 位于南偏西30°方向,该轮船沿正南方向以 15 海里/时的速度匀速航行 2 小时后到达 N 处,再观测灯塔 P 位于南偏西 60° 方向,若该轮船继续向南航行至灯塔 P 最近的位置 T 处,此时轮船与灯塔之间的距离 PT 为 海里(结果保留根号).
解析:由题意得,MN =15×2=30(海里).
∵ ∠PMN =30° ,∠PNT = 60°,
∴ ∠MPN =∠PMN = 30°,
∴ PN =MN =30 海里.
∵ 该轮船继续向南航行至 T 处距灯塔 P 最近,
∴ PT⊥MT,
∴ PT =PN·sin∠PNT=153海里.
?
跟踪训练
新知探究
知识点2:解与坡度有关的问题
如图,从山脚到山顶有两条路 AB 与 BC,问哪条路比较陡?
A
B
C
如何用数量来表示哪条路陡呢?
新知探究
坡面与水平面的夹角叫做坡角,一般用字母 α,β,γ 表示 .
坡面的铅直高度 ( h ) 和水平宽度 ( l ) 的比叫做坡面的坡度 (或坡比),通常用 i 表示, 即 i = h : l .
α
l
h
i= h : l
坡面
水平面
1.坡度不是角的度数,它是坡角的正切值,即 i =tanα;
2.坡度越大,坡角 α 就越大,坡面就越陡.
新知探究
1.如图,一山坡的坡度为 i=1:2.小刚从山脚 A 出发, 沿山坡向上走了 240 m 到达点 C.这座山坡的坡角约是多少度?小刚上升了约多少米?(角度精确到 0.01°,长度精确到0.1 m)
i=1:2
A
B
C
新知探究
在 Rt△ABC 中,∠B =90°,∠A =26.57°,AC =240 m,
解:
用 α 表示坡角的大小,由题意可得
因此 α≈26.57°.
即这座山坡的坡角约为 26.57°,小刚上升了约 107.3 m.
从而 BC =240×sin26.57°≈107.3(m).
因此
i=1:2
A
B
C
α
新知探究
2.水库大坝的横断面是梯形,坝顶宽 6 m,坝高 23 m,斜坡 AB 的坡度 i1=1∶3,斜坡 CD 的坡度 i2=1∶2.5,求:
(1) 斜坡 CD 的坡角 α (精确到 1°);
A
D
B
C
i2=1:2.5
23
6
α
i1=1:3
解: 斜坡 CD 的坡度 i2= tanα = 1 : 2.5=0.4,
由计算器可算得 α ≈ 22°.
故斜坡 CD 的坡角 α 约为 22°.
新知探究
解:分别过点 B、C 作 BE⊥AD,CF⊥AD,垂足分别
为点 E、 F,由题意可知 BE=CF=23 m , EF=BC=6 m.
(2) 坝底 AD 与斜坡 AB 的长度 (精确到 0.1 m).
E
F
A
D
B
C
23
6
α
i1=1:3
i2=1:2.5
在 Rt△ABE 中,
1
新知探究
=69+6+57.5=132.5 (m).
在 Rt△ABE 中,由勾股定理可得
故坝底 AD 的长度为 132.5 m,斜坡 AB 的长度约为 72.7 m.
E
F
A
D
B
C
i2=1:2.5
23
6
α
i1=1:3
在 Rt△DCF 中,同理可得
2
如图所示,某拦水大坝的横断面为梯形 ABCD,AE,DF 为梯形的高,其中迎水坡 AB 的坡角 α =45°,坡长 AB =62 米,背水坡 CD 的坡度 i=1:3( i 为 DF 与 FC 的比值),则背水坡 CD 的坡长为米.
?
跟踪训练
解析:迎水坡 AB 的坡角 α=45°,坡长 AB =62米,
∴ AE =AB·sinα=62?×sin45°=6(米).
∵ 背水坡 CD 的坡度 i=1: 3( i 为 DF 与 FC 的比值),
∴ tanC =13=33,
∴ ∠C =30°,
∴ CD =2DF =2AE =12米.
?
跟踪训练
随堂练习
1.如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AP=63千米,则A,B两点间的距离为( )千米.
A.4 B.43 C.2 D.6
?
随堂练习
解析:由题意知,∠PAB=30°,∠PBC=60°,
∴∠APB=∠PBC-∠PAB=60°-30°=30°,
∴∠PAB=∠APB,∴AB=PB,
在Rt△PAC中,∵AP=63千米,
∴PC=12PA=33千米,
在Rt△PBC中,∵sin∠PBC=????????????????,
∴PB=????????sin60°?=3332?=6千米.
?
随堂练习
2.为满足广大滑板爱好者的需求,某广场修建了一个小型滑板场,如图,爱好者们从 A 处滑下,经缓冲区 EF 之后,滑向 C 处,已知 AB⊥BD 于点 B,CD⊥BD 于点 D,AB =2CD,BD = 13 m,缓冲区EF =3 m,斜坡轨道 AE 的坡度 i =1:2,斜坡轨道 FC 的坡角为 37°,其中 B、E、F、D 在同一直线上,则 AB 的长度约为( )
(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
A.3.55 m B.3.75 m
C.3.95 m D.4.15 m
A
D
C
B
E
F
随堂练习
解析:∵AB=2CD,∴设CD=x,则AB=2x,
∵tan37°≈0.75,
∴????????????????=?????????????=0.75,则DF=43x,
∵斜坡轨道AE的坡度i=1:2,
∴BE=2AB=4x,
故BD-EF=BE+FD=13-3=4x+43x,
解得x=158,故AB=2× 158?=154?=3.75(m).
?
A
D
C
B
E
F
随堂练习
3.为了维护海洋权益,国家海洋局加大了在南海的巡逻力度,一天,我国两艘海监船刚好在我国某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60(6+2)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(6?2)海里.
?
随堂练习
(1)分别求出 A 与 C 及 B 与 C 的距离 AC、BC;(结果保留根号)
解:(1)如图,过点 C 作 CE⊥AB 于点 E,
可得∠ACE =30°,∠BCE =45°,
设 AE =x 海里,
则在 Rt△ACE 中,CE =3x 海里,AC =2x 海里,
在 Rt△BCE 中,BE =CE =3x 海里,BC =6x 海里.
∵ AB =AE +BE,∴ x+3x=60(6+2),
解得 x =602.
∴ AC =1202 海里,BC = 1203 海里.
?
E
随堂练习
(2)已知在灯塔D周围100海里范围内有暗礁群,我国 A处海监船沿AC前往C处盘查,途中有无触礁的危险?
(参考数据:2≈1.41,3≈1.73,6≈2.45)
?
解:(2)如图,过点 D 作 DF⊥AC 于点 F,
则∠DAF =60°.
在Rt△AFD 中,DF =DA·sin 60°=32DA,
∴ DF =32?×120( 6?2 )=60( 32?6)≈106.8(海里)> 100 海里,
∴ 无触礁危险.
?
F
课堂小结
解直角三角形的应用
方向角问题
坡度问题
坡角
坡度(或坡比):
1.(2019·长沙中考)如图,一艘轮船从位于灯塔 C 的北偏东 60°方向,距离灯塔 60 n mile 的小岛 A 出发,沿正南方向航行一段时间后,到达位于灯塔 C 的南偏东 45°方向上的 B 处,这时轮船 B 与小岛 A 的距离是( )
A.303 n mile
B.60 n mile
C.120 n mile
D. (30+303) n mile
?
对接中考
对接中考
解析:如图,设过点 C 的水平线与 AB 交于点 D.
由题意易知,∠ACD =30°,∠BCD =45°,AC =60 n mile.
在 Rt△ACD 中,sin∠ACD =????????????????,cos∠ACD =?????????????????,
∴AD =AC·sin∠ACD =30 n mile,
CD =AC·cos∠ACD = 60×32=303(n mile).
在 Rt△DCB 中,易知∠B =∠BCD =45°,
∴ BD =CD =303 n mile,
∴ AB =AD+BD =(30+303)n mile.
?
对接中考
2.(2020·仙桃市中考)如图,海中有个小岛 A,一艘轮船由西向东航行,在点 B 处测得小岛 A 位于它的东北方向,此时轮船与小岛相距 20 海里,继续航行至点 D 处,测得小岛 A 在它的北偏西60°方向,此时轮船与小岛的距离 AD 为 海里.
A
B
D
北
东
45°
60°
对接中考
解:如图,过点A作AC⊥BD于点C,
根据题意可知:
∠BAC=∠ABC=45°,∠ADC=30°,AB=20,
在Rt△ABC中,AC=BC=AB·sin45°=20×22=102,
在Rt△ACD中,∠ADC=30°,
∴AD=2AC=202(海里).
?
C
A
B
D
北
东
45°
60°
对接中考
3.(2020·泰安中考)如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC//AD,BE⊥AD,斜坡 AB 长 26 m,斜坡 AB 的坡比为 12:5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过 50°时,可确保山体不滑坡.如果改造时保持
坡脚 A 不动,则坡顶 B 沿 BC 至少向右移
m时,才能确保山体不滑坡.
(取tan50°=1.2)
A
E
D
C
B
对接中考
解:在BC上取点F,使∠FAE=50°,过点F作FH⊥AD于点 H,
∵BF//EH,BE⊥AD,FH⊥AD,
∴四边形BEHF为矩形,
∴BF=EH,BE=FH,
∵斜坡AB的坡比为12:5,
∴????????????????=125,
?
F
H
A
E
D
C
B
对接中考
设BE=12x,则AE=5x,
由勾股定理得,AE2+BE2=AB2,即(5x)2+(12x)2=262,
解得x=2,
∴AE=10,BE=24,∴FH=BE=24,
在Rt△FAH中,tan∠FAH=????????????????,
∴AH=????????tan50°=20,∴BF=EH=AH-AE=10,
∴至少向右移10m时,才能确保山体不滑坡.
?
F
H
A
E
D
C
B
课后作业
请完成课本后习题第5、9题.
