人教版数学九年级下册28章 锐角三角函数小结 课时2课件(34张)
文档属性
| 名称 | 人教版数学九年级下册28章 锐角三角函数小结 课时2课件(34张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览






文档简介
锐角三角函数
人教版-数学-九年级-下册
知识梳理-重点解析-深化练习
28 小结课
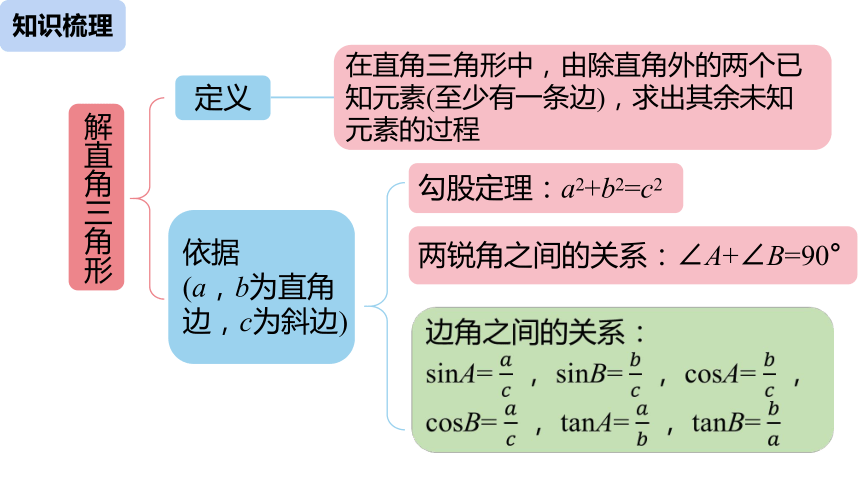
知识梳理
解直角三角形
定义
依据
(a,b为直角边,c为斜边)
勾股定理:a2+b2=c2
两锐角之间的关系:∠A+∠B=90°
边角之间的关系:
sinA= ????????,sinB= ????????,cosA= ????????,cosB= ????????,tanA= ????????,tanB= ????????
?
在直角三角形中,由除直角外的两个已知元素(至少有一条边),求出其余未知元素的过程
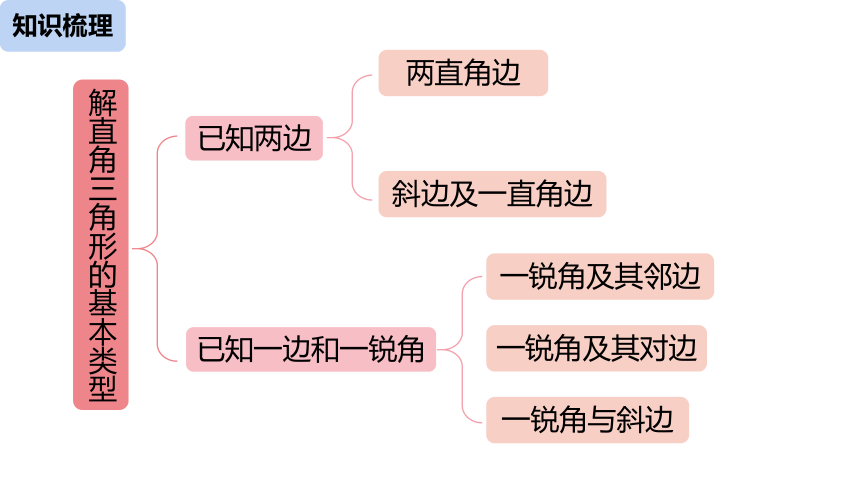
知识梳理
解直角三角形的基本类型
已知两边
已知一边和一锐角
两直角边
斜边及一直角边
一锐角及其邻边
一锐角及其对边
一锐角与斜边
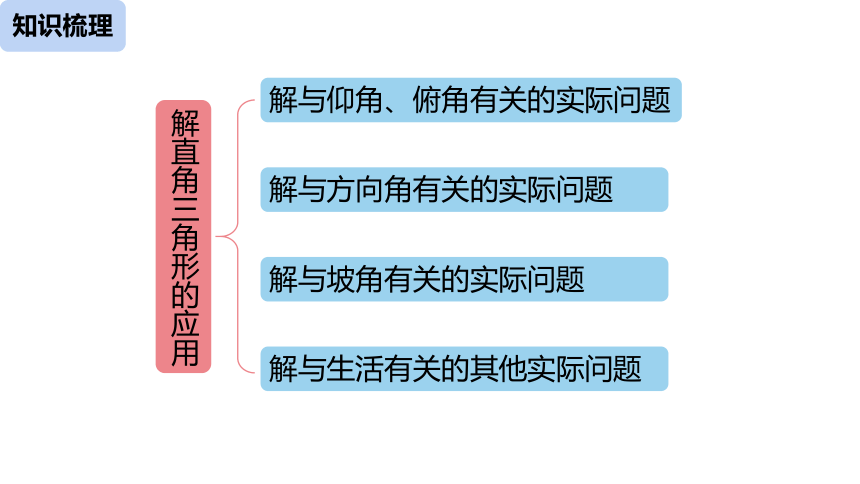
知识梳理
解直角三角形的应用
解与仰角、俯角有关的实际问题
解与方向角有关的实际问题
解与坡角有关的实际问题
解与生活有关的其他实际问题
知识梳理
(1) 在Rt△ABC中,∠C=90°,a,b,c 分别是∠A,∠B,∠C 的对边.
三边关系:___________;
三角关系: ;
边角关系:sinA=cosB=____ ,cosA=sinB = ,
tanA= ,tanB= .
a2+b2=c2
∠A=90°-∠B
5. 解直角三角形
知识梳理
(2) 直角三角形可解的条件
解直角三角形时知道其中的 2 个元素(至少有一个是边),就可以求出其余的 3 个未知元素.
(3)直角三角形的解法
①知一边一锐角:先由两锐角互余关系求出另一锐角;知斜边,再用正弦(或余弦)求另两边;知直角边,用正切求
知识梳理
另一直角边,再用正弦或勾股定理求斜边;
②知两边:先用勾股定理求另一边,再用边角关系求锐角;
③斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题.
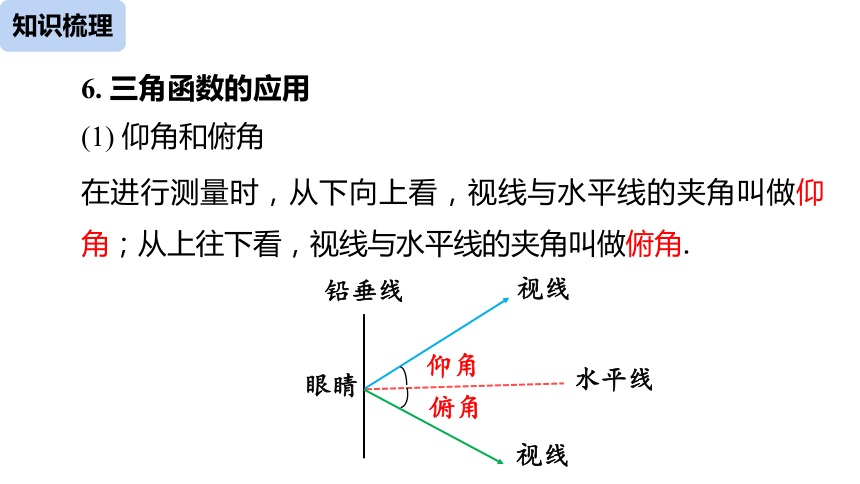
知识梳理
(1) 仰角和俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
6. 三角函数的应用
铅垂线
眼睛
视线
水平线
视线
仰角
俯角
知识梳理
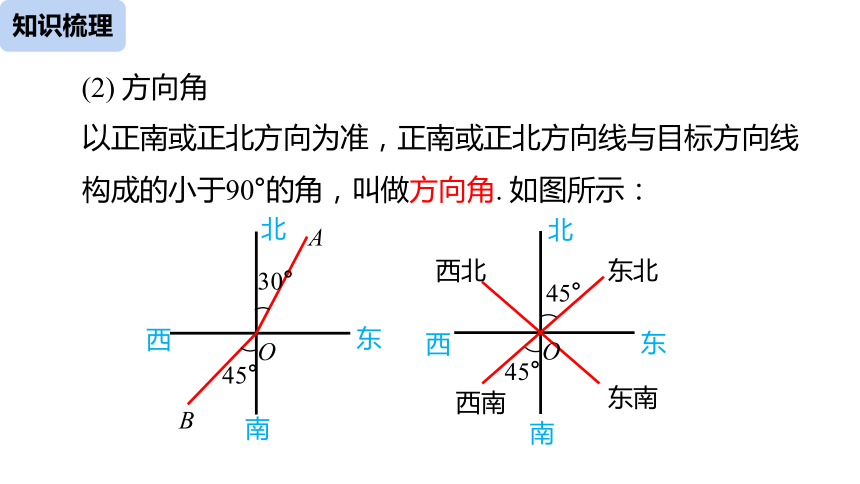
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方向角. 如图所示:
30°
45°
B
O
A
东
西
北
南
(2) 方向角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
知识梳理
坡面与水平面的夹角叫做坡角,记作 α,有 i = tan α.
坡度通常写成 1∶m 的形式,如 i =1∶6.
显然,坡度越大,坡角 α 就越大,
坡面就越陡.
如图:坡面的铅垂高度(h)和水平长度(l)的比叫做坡度.记作 i,即 i = .
(3) 坡度,坡角
知识梳理
将实际问题抽象为数学问题(画出平面图形,
转化为解直角三角形的问题);
根据条件的特点,适当选用锐角三角函数等
去解直角三角形;
得到数学问题的答案;
得到实际问题的答案.
(4) 利用解直角三角形的知识解决实际问题的一般过程:
1
2
3
4
重点解析
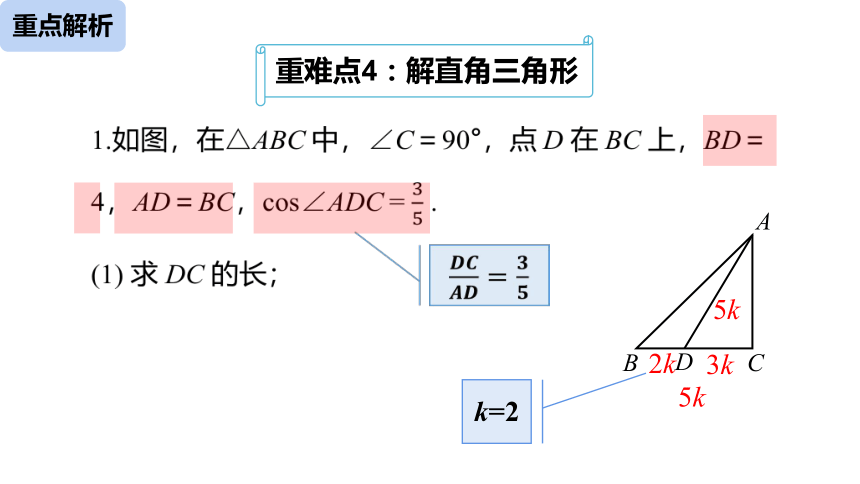
重难点4:解直角三角形
1.如图,在△ABC 中,∠C=90°,点 D 在 BC 上,BD=4,AD=BC,cos∠ADC= 35 .
(1) 求 DC 的长;
?
A
B
C
D
5k
3k
????????????????=????????
?
k=2
5k
2k
重点解析
又 BC-CD=BD,
解得 k =2, ∴ CD = 6.
A
B
C
D
解:在Rt△ACD中,cos∠ADC= ????????????????=35,
设 DC =3k,则 AD =5k,
?
重点解析
(2) 求 sinB 的值.
解:BC=BD+CD=4+6=10=AD,
在Rt△ACD中,
在Rt△ABC中,
A
B
C
D
重点解析
2.已知:如图,Rt△AOB 中,∠O=90°,以 OA 为半径作⊙O,BC 切⊙O 于点 C,连接 AC 交 OB 于点 P.
(1) 求证:BP=BC;
重点解析
解:连接OC.
∵BC是⊙O的切线,
∴∠OCB=90°,
∴∠OCA+∠BCA=90°.
∵OA=OC,∴∠OCA=∠OAC,
∴∠OAC+∠BCA=90°,
∵∠BOA=90°,∴∠OAC+∠APO=90°,
∵∠APO=∠BPC,∴∠BPC=∠BCA,∴BP=BC.
重点解析
解:延长 AO 交⊙O 于点 E,连接 CE,
在 Rt△AOP 中,∵sin∠PAO= 13 ,
设OP=x,则 AP=3x,
∴AO= 22x,AC =3x+7,
∵AO=OE,∴OE= 22x,
∴AE= 42x.
?
(2) 若 sin∠PAO= 13 ,且 PC=7,求⊙O 的半径.
?
E
直径所对的圆周角为直角.
重点解析
∵ sin∠PAO=13, ∴ cos∠PAO =223,
∴在 Rt△ACE中,cos∠CAE=????????????????=223,
∴ 3????+742????=223 ,解得 x=3,
∴AO= 22x=62 ,即⊙O 的半径为 62 .
?
(2) 若 sin∠PAO= 13 ,且 PC=7,求⊙O 的半径.
?
E
重点解析
重难点5:三角函数的应用
1.如图,防洪大堤的横截面是梯形 ABCD,其中 AD∥BC,α=60°,汛期来临前对其进行了加固,改造后的背水面坡角 β=45°.若原坡长 AB =20 m,求改造后的坡长 AE.(结果保留根号)
A
D
C
B
E
α
β
重点解析
解:过点 A 作 AF⊥BC 于点 F,
在 Rt△ABF 中,
∠ABF =∠α=60°,
则 AF=AB·sin60°= 103 (m),
在 Rt△AEF 中,∠E=∠β=45°,
则 ????????=????????sin45°=106 (m).
故改造后的坡长 AE 为 106m.
?
F
A
D
C
B
E
α
β
重点解析
2.如图,某数学活动小组选定测量小河对岸大树 BC 的高度,他们在斜坡上 D 处测得大树顶端B的仰角是 30°,朝大树方向下坡走 6 米到达坡底 A 处,在 A 处测得大树顶端 B 的仰角是 48°,若坡角∠FAE=30°,求大树的高度.(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,
tan48°≈1.11, 3 ≈1.73)
?
重点解析
解:如图,过点 D 作 DG⊥BC 于点 G,DH⊥CE 于点 H,
则四边形 DHCG 为矩形.
故 DG=CH,CG=DH,DG∥HC,
∴∠DAH=∠FAE=30°,
在 Rt△AHD 中,
∵∠DAH=30°,AD=6,
∴DH=3,AH= 33 ,
∴CG=3,
?
G
H
重点解析
设 BC 为 x,在 Rt△ABC 中,
????????=????????tan∠????????????=????1.11 ,
?
在 Rt△BDG 中,∵ BG=DG · tan30°,
∴
∴
解得 x ≈13,
∴大树的高度约为 13 米.
G
H
重点解析
3.如图,轮船甲位于码头 O 的正西方向 A 处,轮船乙位于码头 O 的正北方向 C 处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为 45 km/h 和 36 km/h,经过 0.1 h,轮船甲行驶至 B 处,轮船乙行驶至 D 处,测得∠DBO=58°,此时 B 处
距离码头 O 多远?(参考数据:sin58°≈0.85,
cos58°≈0.53,tan58°≈1.60)
重点解析
解:设 B 处距离码头 O x km,
在Rt△CAO 中,∠CAO=45°,
∴CO=AO · tan∠CAO=(45×0.1+x)· tan45°=4.5+x,
在Rt△DBO中,∠DBO=58°,
∴DO=BO · tan∠DBO=x · tan58°,
∵DC=DO-CO,
∵tan∠CAO = ,
∵tan∠DBO = ,
重点解析
∴36×0.1=x · tan58°-(4.5+x),
此时 B 处距离码头 O 约13.5 km.
∴
深化练习
1.如图所示,在 Rt△ABC 中,∠C=90°,AC= 3 .点 D 为 BC 边上一点,且 BD=2AD,∠ADC=60°.求△ABC 的周长 (结果保留根号).
?
深化练习
∴ BD=2AD=4.
∴ BC=BD+DC=5.
解:在 Rt△ADC 中,
在 Rt△ABC 中,
∴ △ABC 的周长为 AB+BC+AC
深化练习
2.如图,AB 为⊙O 的直径,且弦 CD⊥AB 于点 E,过点 B 的切线与 AD 的延长线交于点 F.若cos∠C = 45 ,DF=3,
求⊙O 的半径.
?
深化练习
解:连接 BD.
在⊙O 中,∠C =∠A,
∵BF 是⊙O 的切线,∴∠ABF=90°.
设 AB=4x,则 AF=5x,
由勾股定理得,BF=3x.
∵AB是⊙O 的直径,∴BD⊥AD,
∴cosA =cosC =
∴△ABF∽△BDF,
∴⊙O的半径为
∴
深化练习
3.如图,某防洪指挥部发现长江边一处防洪大堤 (横断面为梯形 ABCD) 急需加固,背水坡的坡角为45°,高10米.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽 2米,加固后背水坡EF的坡比
i=1:3 .求加固后坝底增加的宽度AF. (结果保留根号)
?
A
B
C
D
E
F
45°
i=1:
深化练习
A
B
C
D
E
F
45°
i=1:
G
H
解:作 DG⊥AB 于点 G,EH⊥AB 于点 H,
则 GH=DE=2 米,EH=DG=10 米.
(米),
(米).
又∵AG=DG=10米,
∴ (米).
故加固后坝底增加的宽度 AF 为 米.
深化练习
4.如图,为了测出某塔 CD 的高度,在塔前的平地上选择一点 A,用测角仪测得塔顶 D 的仰角为30°,在A、C 之间选择一点 B(A、B、C 三点在同一直线上).用测角仪测得塔顶 D 的仰角为75°,且 AB 间的距离为 40 m.
(1) 求点 B 到 AD 的距离;
E
75°
30°
A
B
C
D
解:(1) 过点 B 作 BE⊥AD 于点 E.
在 Rt△ABE 中,∵∠A=30°,
∴BE = 12AB=20m.
?
深化练习
(2) 求塔高CD (结果用根号表示).
解:(2)在 Rt△ABE 中,
∵∠A=30°,∴∠ABE=60°,
∵∠DBC=75°,∴∠EBD=180°-60°-75°=45°,
∴DE=EB=20 m,
则 AD=AE+DE= 203+20(m),
在 Rt△ADC 中,∠A=30°,
∴ ????????=????????2=10+103(m).
?
E
75°
30°
A
B
D
C
人教版-数学-九年级-下册
知识梳理-重点解析-深化练习
28 小结课
知识梳理
解直角三角形
定义
依据
(a,b为直角边,c为斜边)
勾股定理:a2+b2=c2
两锐角之间的关系:∠A+∠B=90°
边角之间的关系:
sinA= ????????,sinB= ????????,cosA= ????????,cosB= ????????,tanA= ????????,tanB= ????????
?
在直角三角形中,由除直角外的两个已知元素(至少有一条边),求出其余未知元素的过程
知识梳理
解直角三角形的基本类型
已知两边
已知一边和一锐角
两直角边
斜边及一直角边
一锐角及其邻边
一锐角及其对边
一锐角与斜边
知识梳理
解直角三角形的应用
解与仰角、俯角有关的实际问题
解与方向角有关的实际问题
解与坡角有关的实际问题
解与生活有关的其他实际问题
知识梳理
(1) 在Rt△ABC中,∠C=90°,a,b,c 分别是∠A,∠B,∠C 的对边.
三边关系:___________;
三角关系: ;
边角关系:sinA=cosB=____ ,cosA=sinB = ,
tanA= ,tanB= .
a2+b2=c2
∠A=90°-∠B
5. 解直角三角形
知识梳理
(2) 直角三角形可解的条件
解直角三角形时知道其中的 2 个元素(至少有一个是边),就可以求出其余的 3 个未知元素.
(3)直角三角形的解法
①知一边一锐角:先由两锐角互余关系求出另一锐角;知斜边,再用正弦(或余弦)求另两边;知直角边,用正切求
知识梳理
另一直角边,再用正弦或勾股定理求斜边;
②知两边:先用勾股定理求另一边,再用边角关系求锐角;
③斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题.
知识梳理
(1) 仰角和俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
6. 三角函数的应用
铅垂线
眼睛
视线
水平线
视线
仰角
俯角
知识梳理
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方向角. 如图所示:
30°
45°
B
O
A
东
西
北
南
(2) 方向角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
知识梳理
坡面与水平面的夹角叫做坡角,记作 α,有 i = tan α.
坡度通常写成 1∶m 的形式,如 i =1∶6.
显然,坡度越大,坡角 α 就越大,
坡面就越陡.
如图:坡面的铅垂高度(h)和水平长度(l)的比叫做坡度.记作 i,即 i = .
(3) 坡度,坡角
知识梳理
将实际问题抽象为数学问题(画出平面图形,
转化为解直角三角形的问题);
根据条件的特点,适当选用锐角三角函数等
去解直角三角形;
得到数学问题的答案;
得到实际问题的答案.
(4) 利用解直角三角形的知识解决实际问题的一般过程:
1
2
3
4
重点解析
重难点4:解直角三角形
1.如图,在△ABC 中,∠C=90°,点 D 在 BC 上,BD=4,AD=BC,cos∠ADC= 35 .
(1) 求 DC 的长;
?
A
B
C
D
5k
3k
????????????????=????????
?
k=2
5k
2k
重点解析
又 BC-CD=BD,
解得 k =2, ∴ CD = 6.
A
B
C
D
解:在Rt△ACD中,cos∠ADC= ????????????????=35,
设 DC =3k,则 AD =5k,
?
重点解析
(2) 求 sinB 的值.
解:BC=BD+CD=4+6=10=AD,
在Rt△ACD中,
在Rt△ABC中,
A
B
C
D
重点解析
2.已知:如图,Rt△AOB 中,∠O=90°,以 OA 为半径作⊙O,BC 切⊙O 于点 C,连接 AC 交 OB 于点 P.
(1) 求证:BP=BC;
重点解析
解:连接OC.
∵BC是⊙O的切线,
∴∠OCB=90°,
∴∠OCA+∠BCA=90°.
∵OA=OC,∴∠OCA=∠OAC,
∴∠OAC+∠BCA=90°,
∵∠BOA=90°,∴∠OAC+∠APO=90°,
∵∠APO=∠BPC,∴∠BPC=∠BCA,∴BP=BC.
重点解析
解:延长 AO 交⊙O 于点 E,连接 CE,
在 Rt△AOP 中,∵sin∠PAO= 13 ,
设OP=x,则 AP=3x,
∴AO= 22x,AC =3x+7,
∵AO=OE,∴OE= 22x,
∴AE= 42x.
?
(2) 若 sin∠PAO= 13 ,且 PC=7,求⊙O 的半径.
?
E
直径所对的圆周角为直角.
重点解析
∵ sin∠PAO=13, ∴ cos∠PAO =223,
∴在 Rt△ACE中,cos∠CAE=????????????????=223,
∴ 3????+742????=223 ,解得 x=3,
∴AO= 22x=62 ,即⊙O 的半径为 62 .
?
(2) 若 sin∠PAO= 13 ,且 PC=7,求⊙O 的半径.
?
E
重点解析
重难点5:三角函数的应用
1.如图,防洪大堤的横截面是梯形 ABCD,其中 AD∥BC,α=60°,汛期来临前对其进行了加固,改造后的背水面坡角 β=45°.若原坡长 AB =20 m,求改造后的坡长 AE.(结果保留根号)
A
D
C
B
E
α
β
重点解析
解:过点 A 作 AF⊥BC 于点 F,
在 Rt△ABF 中,
∠ABF =∠α=60°,
则 AF=AB·sin60°= 103 (m),
在 Rt△AEF 中,∠E=∠β=45°,
则 ????????=????????sin45°=106 (m).
故改造后的坡长 AE 为 106m.
?
F
A
D
C
B
E
α
β
重点解析
2.如图,某数学活动小组选定测量小河对岸大树 BC 的高度,他们在斜坡上 D 处测得大树顶端B的仰角是 30°,朝大树方向下坡走 6 米到达坡底 A 处,在 A 处测得大树顶端 B 的仰角是 48°,若坡角∠FAE=30°,求大树的高度.(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,
tan48°≈1.11, 3 ≈1.73)
?
重点解析
解:如图,过点 D 作 DG⊥BC 于点 G,DH⊥CE 于点 H,
则四边形 DHCG 为矩形.
故 DG=CH,CG=DH,DG∥HC,
∴∠DAH=∠FAE=30°,
在 Rt△AHD 中,
∵∠DAH=30°,AD=6,
∴DH=3,AH= 33 ,
∴CG=3,
?
G
H
重点解析
设 BC 为 x,在 Rt△ABC 中,
????????=????????tan∠????????????=????1.11 ,
?
在 Rt△BDG 中,∵ BG=DG · tan30°,
∴
∴
解得 x ≈13,
∴大树的高度约为 13 米.
G
H
重点解析
3.如图,轮船甲位于码头 O 的正西方向 A 处,轮船乙位于码头 O 的正北方向 C 处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为 45 km/h 和 36 km/h,经过 0.1 h,轮船甲行驶至 B 处,轮船乙行驶至 D 处,测得∠DBO=58°,此时 B 处
距离码头 O 多远?(参考数据:sin58°≈0.85,
cos58°≈0.53,tan58°≈1.60)
重点解析
解:设 B 处距离码头 O x km,
在Rt△CAO 中,∠CAO=45°,
∴CO=AO · tan∠CAO=(45×0.1+x)· tan45°=4.5+x,
在Rt△DBO中,∠DBO=58°,
∴DO=BO · tan∠DBO=x · tan58°,
∵DC=DO-CO,
∵tan∠CAO = ,
∵tan∠DBO = ,
重点解析
∴36×0.1=x · tan58°-(4.5+x),
此时 B 处距离码头 O 约13.5 km.
∴
深化练习
1.如图所示,在 Rt△ABC 中,∠C=90°,AC= 3 .点 D 为 BC 边上一点,且 BD=2AD,∠ADC=60°.求△ABC 的周长 (结果保留根号).
?
深化练习
∴ BD=2AD=4.
∴ BC=BD+DC=5.
解:在 Rt△ADC 中,
在 Rt△ABC 中,
∴ △ABC 的周长为 AB+BC+AC
深化练习
2.如图,AB 为⊙O 的直径,且弦 CD⊥AB 于点 E,过点 B 的切线与 AD 的延长线交于点 F.若cos∠C = 45 ,DF=3,
求⊙O 的半径.
?
深化练习
解:连接 BD.
在⊙O 中,∠C =∠A,
∵BF 是⊙O 的切线,∴∠ABF=90°.
设 AB=4x,则 AF=5x,
由勾股定理得,BF=3x.
∵AB是⊙O 的直径,∴BD⊥AD,
∴cosA =cosC =
∴△ABF∽△BDF,
∴⊙O的半径为
∴
深化练习
3.如图,某防洪指挥部发现长江边一处防洪大堤 (横断面为梯形 ABCD) 急需加固,背水坡的坡角为45°,高10米.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽 2米,加固后背水坡EF的坡比
i=1:3 .求加固后坝底增加的宽度AF. (结果保留根号)
?
A
B
C
D
E
F
45°
i=1:
深化练习
A
B
C
D
E
F
45°
i=1:
G
H
解:作 DG⊥AB 于点 G,EH⊥AB 于点 H,
则 GH=DE=2 米,EH=DG=10 米.
(米),
(米).
又∵AG=DG=10米,
∴ (米).
故加固后坝底增加的宽度 AF 为 米.
深化练习
4.如图,为了测出某塔 CD 的高度,在塔前的平地上选择一点 A,用测角仪测得塔顶 D 的仰角为30°,在A、C 之间选择一点 B(A、B、C 三点在同一直线上).用测角仪测得塔顶 D 的仰角为75°,且 AB 间的距离为 40 m.
(1) 求点 B 到 AD 的距离;
E
75°
30°
A
B
C
D
解:(1) 过点 B 作 BE⊥AD 于点 E.
在 Rt△ABE 中,∵∠A=30°,
∴BE = 12AB=20m.
?
深化练习
(2) 求塔高CD (结果用根号表示).
解:(2)在 Rt△ABE 中,
∵∠A=30°,∴∠ABE=60°,
∵∠DBC=75°,∴∠EBD=180°-60°-75°=45°,
∴DE=EB=20 m,
则 AD=AE+DE= 203+20(m),
在 Rt△ADC 中,∠A=30°,
∴ ????????=????????2=10+103(m).
?
E
75°
30°
A
B
D
C
