人教版数学九年级下册28章 锐角三角函数数学活动课件(29张PPT)
文档属性
| 名称 | 人教版数学九年级下册28章 锐角三角函数数学活动课件(29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 23:51:45 | ||
图片预览





文档简介
28 数学活动
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
我们学过哪些利用相似三角形知识测量物体高度的方法?
利用影子测量物体的高度.
利用平面镜的反射测量物体的高度.
借助标杆测量物体的高度.
学习目标
1.会制作测角仪,应用制作的测角仪测量实物的高度,体会三角函数和解直角三角形在实际生活中的应用价值.
2.在实际操作中培养学生分析问题、解决问题的能力.
课堂导入
在学习了本章内容以后,你能用解直角三角形知识测量物体的高度吗?
新知探究
知识点1:制作测角仪
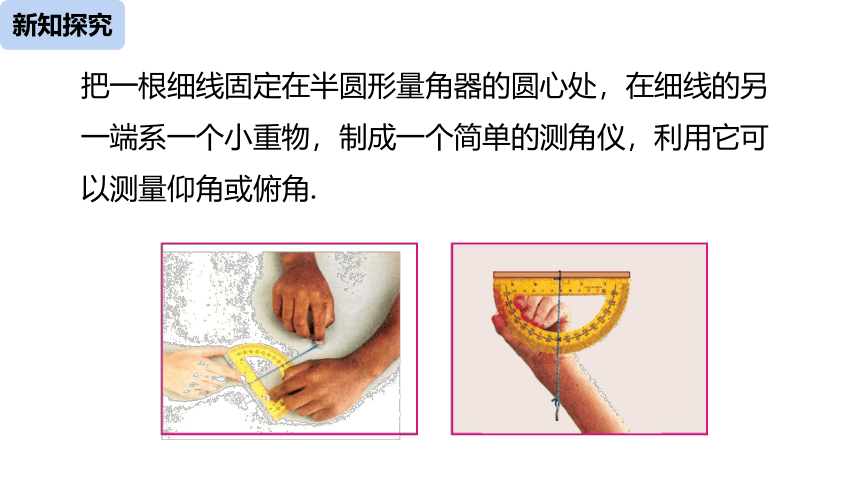
利用解直角三角形知识测量物体的高度,我们需要先测量角度的大小,你能用下面的物品制作一个简易的测角仪器吗?
新知探究
把一根细线固定在半圆形量角器的圆心处,在细线的另一端系一个小重物,制成一个简单的测角仪,利用它可以测量仰角或俯角.
新知探究
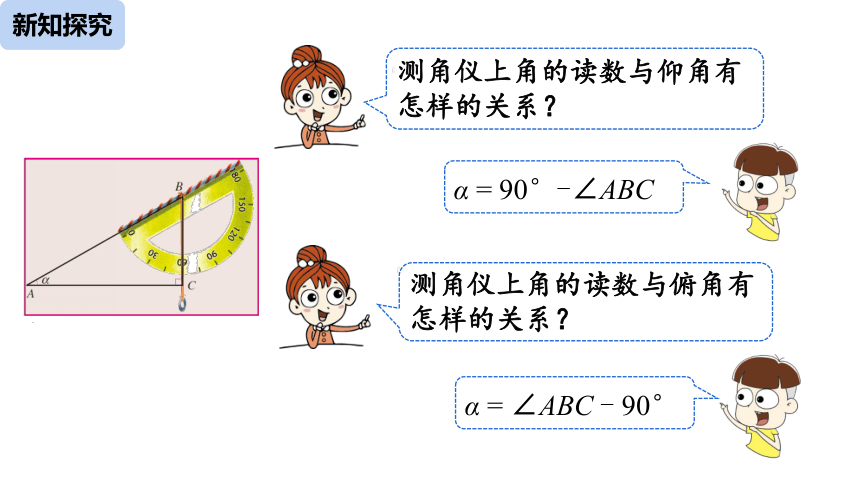
如何使用测角仪呢?
将仪器用手托起,拿到眼前,使视线沿着仪器的直径刚好到达树的最高点(如图).
新知探究
α = 90°-∠ABC
α = ∠ABC - 90°
测角仪上角的读数与仰角有怎样的关系?
测角仪上角的读数与俯角有怎样的关系?
新知探究
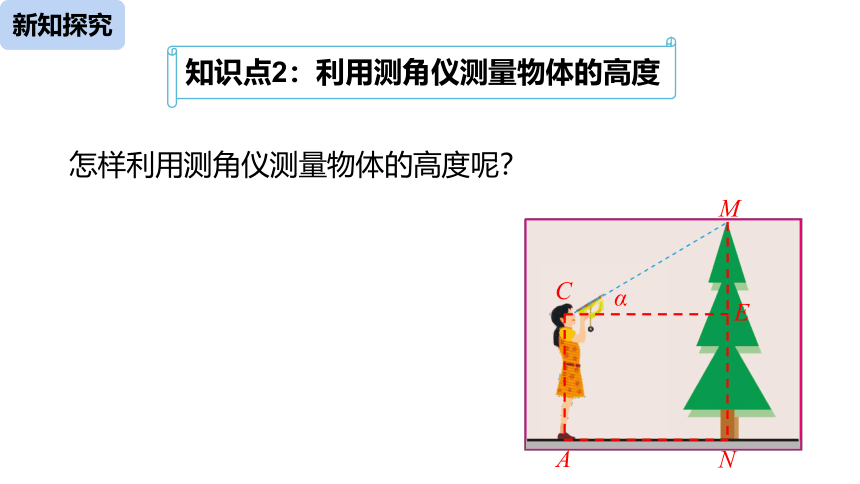
知识点2:利用测角仪测量物体的高度
怎样利用测角仪测量物体的高度呢?
A
C
M
N
E
α
新知探究
①在测点 A 安置测角仪,测得 M 的仰角∠MCE= α;
②量出测点 A 到物体底部 N 的水平距离 AN=l;
③量出测角仪的高度 AC = a,可求出
MN = ME + EN = l · tanα + a.
测量底部可以到达的物体的高度步骤:
A
C
M
N
E
α
a
l
新知探究
若不能直接测出AN的长度,还有别的方法可以测出物体的高度吗?
B
D
M
N
β
A
C
α
知识梳理
测量底部不能到达的物体的高度步骤:
①在测点 A 处安置测角仪,测得此时 M 的仰角∠MCE =α;
②在测点 A 与物体之间的B处安置测角仪,测得此时 M 的仰角∠MDE =β;
A
C
B
D
M
N
E
α
β
a
知识梳理
③量出测角仪的高度 AC =BD =a,以及测点 A,B 之间的距离 AB =b.根据测量数据,可求出物体高度 MN 的方程 ,解这个方程就可以求出塔高 MN.
A
C
B
D
M
N
E
α
β
a
b
跟踪训练
如图,某数学兴趣小组想测量一棵树 CD 的高度,他们先在点 A 处测得树顶 C 的仰角为 30°,然后沿 AD 方向前行 10 m 到达 B 点,在 B 处测得树顶 C 的仰角为 60° (A、B、D 三点在同一直线上).请你根据他们的测量数据计算这棵树的高度(结果精确到 0.1 m).
解:设CD=x.
∴AB=AD-BD,
在Rt△BCD中,BD=
在Rt△ACD中,
即
跟踪训练
∴
随堂练习
1.如图,为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB的高度等于( )
A. 12( 3 +1) m
B. 12( 3 -1) m
C. 6( 3 +1) m
D. 6( 3 -1) m
?
????????tan30°=3????????
?
3?1????????=12
?
C
B
A
C
D
????????tan45°=????????
?
随堂练习
2.如图,某大楼 DE 的顶部竖有一块广告牌 CD,小林在山坡的坡脚 A 处测得广告牌底部 D 的仰角为 53°,沿坡面 AB 向上走到 B 处测得广告牌顶部 C 的仰角为45°.已知山坡 AB 的坡度为 i=1:2.4,AB =26米,AE =30米.则
广告牌 CD 的高度约为( )米.(参考数据:
tan 37°≈0.75,sin 37° ≈ 0.60,cos 37°≈0.80)
A.35 B.30
C.24 D.20
随堂练习
解:过B作BG⊥DE于点G,BH⊥EA的延长线于点H,
则BG=AH+AE,GE=BH,
在Rt△ABH 中,i=tan∠BAH=1:2.4=????????????????,
∴AH=2.4BH,
∴AB=????????2+????????2=2.6BH=26,
∴BH=10,AH=24,
∴BG=AH+AE=24+30=54,
?
G
H
随堂练习
在Rt△BGC中,∠CBG=45°,
∴CG=BG=54.
在Rt△ADE中,∠DAE=53°,
∴∠ADE=90°-53°=37°,
∵tan∠ADE=????????????????=tan37°≈0.75,
∴DE≈43AE≈40.
∴CD=CG+GE-DE≈54+10-40≈24(米).
?
G
H
随堂练习
3.小明为了测量一楼房AB的高度,如图,小明从楼底B出发走了10米到达一坡角(即∠DCM)为30°的斜坡的底部,再走12米到达一观测平台,测得楼顶A的仰角∠ADH为37°,则楼房AB的高度约为( )米.(参考数据:cos37° ≈ 0.80,tan37° ≈ 0.75,3 ≈1.7)
A.15 B.21
C.22 D.16
?
随堂练习
解:过点 D 作DN⊥BM于点 N,
则HB=DN,DH=BN,
∵∠DCN=30°,CD=12,
∴HB=DN=12CD=6,
CN=3DN=63?,
∴DH=BN=BC+CN=10+63?,
?
N
随堂练习
在Rt△ADH中,tan∠ADH=????????????????=tan37°≈ 0.75,
∴AH≈ 0.75DH ≈ 0.75×(10+63) ≈ 15.29,
∴AB=AH+HB ≈ 15.29 +6≈21(米),
即楼房AB的高度约为21米.
?
N
MN = ME + EN = l · tanα + a.
课堂小结
测量物体的高度
底部能到达
底部不能到达
A
C
M
N
E
α
a
A
C
B
D
M
N
E
α
β
a
b
对接中考
1.(2020·温州中考)如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪的高AD为1.5米,则铁塔的高BC为( )
A.(1.5+150tanα)米
B.(1.5+ 150tan???? )米
C.(1.5+150sinα)米
D.(1.5+ 150sin???? )米
?
150tanα
1.5
A
E
对接中考
2.(2020·乐山中考)如图是某商场营业大厅自动扶梯示意图.自动扶梯 AB 的倾斜角为 30°,在自动扶梯下方地面 C 处测得扶梯顶端 B 的仰角为 60°,A、C 之间的距离为4 m,则自动扶梯的垂直高度 BD=? m.(结果保留根号)
4 m
30°
BCsin60°
23
?
对接中考
3.(2020·重庆中考)如图,垂直于水平面的5G信号塔 AB 建在垂直于水平面的悬崖边 B 点处,某测量员从山脚 C 点出发沿水平方向前行 78 米到 D 点(点 A,B,C 在同一直线上),再沿斜坡 DE 方向前行 78 米到 E 点(点 A,B,C,D,E 在同一平面内),在点 E 处测得 5G 信号塔顶端 A 的仰角为 43°,悬崖 BC 的高为 144.5 米,斜坡 DE 的坡度 i=1:2.4,则信号塔 AB 的高度约为( )
(参考数据:sin43°≈0.68,cos43°≈ 0.73,tan43°≈ 0.93)
A.23米 B.24米
C.24.5米 D.25米
对接中考
解:过点 E 作 EF⊥CD, 交 CD 的延长线于点 F,过点 E作 EM⊥AC 于点M,
∵ 斜坡 DE 的坡度 i=1:2.4,DE=CD=78米,
∴ 设 EF =x,则 DF=2.4x.
在 Rt△DEF 中,∵ EF2+DF2=DE2,
即 x2+(2.4x)2=782,解得 x=30,
∴ EF=30米,DF=72米,
∴ CF=DF+DC=72+78=150 米.
M
F
对接中考
∵ EM⊥AC,AC⊥CD,EF⊥CD,
∴ 四边形 EFCM 是矩形,
∴ EM=CF=150米,CM=EF=30米.
在 Rt△AEM 中,∵ ∠AEM=43°,
∴ AM=EM·tan43°≈150×0.93=139.5米,
∴ AC=AM+CM=139.5+30=169.5米.
∴ AB=AC-BC=169.5-144.5=25米.
M
F
课后作业
请完成课本后习题第8题.
锐角三角函数
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
我们学过哪些利用相似三角形知识测量物体高度的方法?
利用影子测量物体的高度.
利用平面镜的反射测量物体的高度.
借助标杆测量物体的高度.
学习目标
1.会制作测角仪,应用制作的测角仪测量实物的高度,体会三角函数和解直角三角形在实际生活中的应用价值.
2.在实际操作中培养学生分析问题、解决问题的能力.
课堂导入
在学习了本章内容以后,你能用解直角三角形知识测量物体的高度吗?
新知探究
知识点1:制作测角仪
利用解直角三角形知识测量物体的高度,我们需要先测量角度的大小,你能用下面的物品制作一个简易的测角仪器吗?
新知探究
把一根细线固定在半圆形量角器的圆心处,在细线的另一端系一个小重物,制成一个简单的测角仪,利用它可以测量仰角或俯角.
新知探究
如何使用测角仪呢?
将仪器用手托起,拿到眼前,使视线沿着仪器的直径刚好到达树的最高点(如图).
新知探究
α = 90°-∠ABC
α = ∠ABC - 90°
测角仪上角的读数与仰角有怎样的关系?
测角仪上角的读数与俯角有怎样的关系?
新知探究
知识点2:利用测角仪测量物体的高度
怎样利用测角仪测量物体的高度呢?
A
C
M
N
E
α
新知探究
①在测点 A 安置测角仪,测得 M 的仰角∠MCE= α;
②量出测点 A 到物体底部 N 的水平距离 AN=l;
③量出测角仪的高度 AC = a,可求出
MN = ME + EN = l · tanα + a.
测量底部可以到达的物体的高度步骤:
A
C
M
N
E
α
a
l
新知探究
若不能直接测出AN的长度,还有别的方法可以测出物体的高度吗?
B
D
M
N
β
A
C
α
知识梳理
测量底部不能到达的物体的高度步骤:
①在测点 A 处安置测角仪,测得此时 M 的仰角∠MCE =α;
②在测点 A 与物体之间的B处安置测角仪,测得此时 M 的仰角∠MDE =β;
A
C
B
D
M
N
E
α
β
a
知识梳理
③量出测角仪的高度 AC =BD =a,以及测点 A,B 之间的距离 AB =b.根据测量数据,可求出物体高度 MN 的方程 ,解这个方程就可以求出塔高 MN.
A
C
B
D
M
N
E
α
β
a
b
跟踪训练
如图,某数学兴趣小组想测量一棵树 CD 的高度,他们先在点 A 处测得树顶 C 的仰角为 30°,然后沿 AD 方向前行 10 m 到达 B 点,在 B 处测得树顶 C 的仰角为 60° (A、B、D 三点在同一直线上).请你根据他们的测量数据计算这棵树的高度(结果精确到 0.1 m).
解:设CD=x.
∴AB=AD-BD,
在Rt△BCD中,BD=
在Rt△ACD中,
即
跟踪训练
∴
随堂练习
1.如图,为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB的高度等于( )
A. 12( 3 +1) m
B. 12( 3 -1) m
C. 6( 3 +1) m
D. 6( 3 -1) m
?
????????tan30°=3????????
?
3?1????????=12
?
C
B
A
C
D
????????tan45°=????????
?
随堂练习
2.如图,某大楼 DE 的顶部竖有一块广告牌 CD,小林在山坡的坡脚 A 处测得广告牌底部 D 的仰角为 53°,沿坡面 AB 向上走到 B 处测得广告牌顶部 C 的仰角为45°.已知山坡 AB 的坡度为 i=1:2.4,AB =26米,AE =30米.则
广告牌 CD 的高度约为( )米.(参考数据:
tan 37°≈0.75,sin 37° ≈ 0.60,cos 37°≈0.80)
A.35 B.30
C.24 D.20
随堂练习
解:过B作BG⊥DE于点G,BH⊥EA的延长线于点H,
则BG=AH+AE,GE=BH,
在Rt△ABH 中,i=tan∠BAH=1:2.4=????????????????,
∴AH=2.4BH,
∴AB=????????2+????????2=2.6BH=26,
∴BH=10,AH=24,
∴BG=AH+AE=24+30=54,
?
G
H
随堂练习
在Rt△BGC中,∠CBG=45°,
∴CG=BG=54.
在Rt△ADE中,∠DAE=53°,
∴∠ADE=90°-53°=37°,
∵tan∠ADE=????????????????=tan37°≈0.75,
∴DE≈43AE≈40.
∴CD=CG+GE-DE≈54+10-40≈24(米).
?
G
H
随堂练习
3.小明为了测量一楼房AB的高度,如图,小明从楼底B出发走了10米到达一坡角(即∠DCM)为30°的斜坡的底部,再走12米到达一观测平台,测得楼顶A的仰角∠ADH为37°,则楼房AB的高度约为( )米.(参考数据:cos37° ≈ 0.80,tan37° ≈ 0.75,3 ≈1.7)
A.15 B.21
C.22 D.16
?
随堂练习
解:过点 D 作DN⊥BM于点 N,
则HB=DN,DH=BN,
∵∠DCN=30°,CD=12,
∴HB=DN=12CD=6,
CN=3DN=63?,
∴DH=BN=BC+CN=10+63?,
?
N
随堂练习
在Rt△ADH中,tan∠ADH=????????????????=tan37°≈ 0.75,
∴AH≈ 0.75DH ≈ 0.75×(10+63) ≈ 15.29,
∴AB=AH+HB ≈ 15.29 +6≈21(米),
即楼房AB的高度约为21米.
?
N
MN = ME + EN = l · tanα + a.
课堂小结
测量物体的高度
底部能到达
底部不能到达
A
C
M
N
E
α
a
A
C
B
D
M
N
E
α
β
a
b
对接中考
1.(2020·温州中考)如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪的高AD为1.5米,则铁塔的高BC为( )
A.(1.5+150tanα)米
B.(1.5+ 150tan???? )米
C.(1.5+150sinα)米
D.(1.5+ 150sin???? )米
?
150tanα
1.5
A
E
对接中考
2.(2020·乐山中考)如图是某商场营业大厅自动扶梯示意图.自动扶梯 AB 的倾斜角为 30°,在自动扶梯下方地面 C 处测得扶梯顶端 B 的仰角为 60°,A、C 之间的距离为4 m,则自动扶梯的垂直高度 BD=? m.(结果保留根号)
4 m
30°
BCsin60°
23
?
对接中考
3.(2020·重庆中考)如图,垂直于水平面的5G信号塔 AB 建在垂直于水平面的悬崖边 B 点处,某测量员从山脚 C 点出发沿水平方向前行 78 米到 D 点(点 A,B,C 在同一直线上),再沿斜坡 DE 方向前行 78 米到 E 点(点 A,B,C,D,E 在同一平面内),在点 E 处测得 5G 信号塔顶端 A 的仰角为 43°,悬崖 BC 的高为 144.5 米,斜坡 DE 的坡度 i=1:2.4,则信号塔 AB 的高度约为( )
(参考数据:sin43°≈0.68,cos43°≈ 0.73,tan43°≈ 0.93)
A.23米 B.24米
C.24.5米 D.25米
对接中考
解:过点 E 作 EF⊥CD, 交 CD 的延长线于点 F,过点 E作 EM⊥AC 于点M,
∵ 斜坡 DE 的坡度 i=1:2.4,DE=CD=78米,
∴ 设 EF =x,则 DF=2.4x.
在 Rt△DEF 中,∵ EF2+DF2=DE2,
即 x2+(2.4x)2=782,解得 x=30,
∴ EF=30米,DF=72米,
∴ CF=DF+DC=72+78=150 米.
M
F
对接中考
∵ EM⊥AC,AC⊥CD,EF⊥CD,
∴ 四边形 EFCM 是矩形,
∴ EM=CF=150米,CM=EF=30米.
在 Rt△AEM 中,∵ ∠AEM=43°,
∴ AM=EM·tan43°≈150×0.93=139.5米,
∴ AC=AM+CM=139.5+30=169.5米.
∴ AB=AC-BC=169.5-144.5=25米.
M
F
课后作业
请完成课本后习题第8题.
