人教版数学九年级下册29.2 三视图 课时4课件(27张)
文档属性
| 名称 | 人教版数学九年级下册29.2 三视图 课时4课件(27张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 698.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览





文档简介
29.2 三视图
投影与视图
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
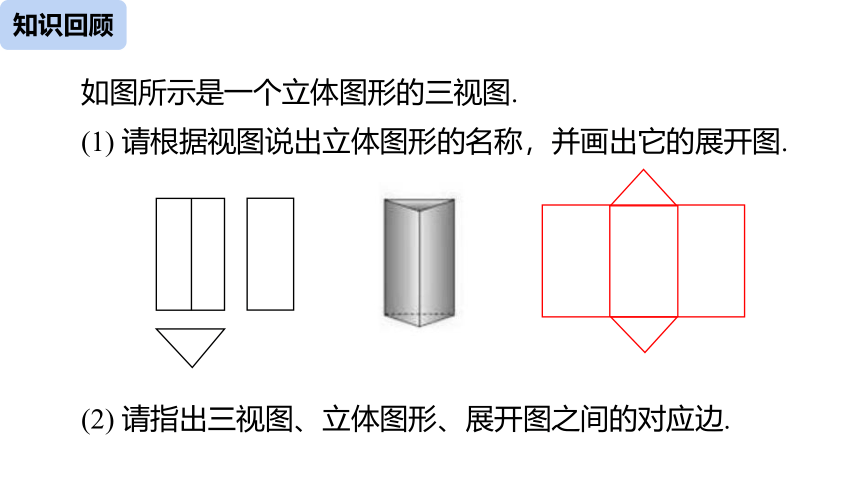
如图所示是一个立体图形的三视图.
(1) 请根据视图说出立体图形的名称,并画出它的展开图.
(2) 请指出三视图、立体图形、展开图之间的对应边.
学习目标
1.能熟练地画出物体的三视图和由三视图想象出物体形状,进一步提高空间想象能力.
2.由三视图想象出立体图形后能进行简单的面积或体积的计算.
课堂导入
在实际生活中,我们研究一个几何体通常要知道它的表面积和体积,那么根据几何体的三视图能否求出几何体的表面积和体积呢?本节课我们就来研究根据物体三视图求其展开图形的面积问题.
新知探究
知识点:三视图的有关计算
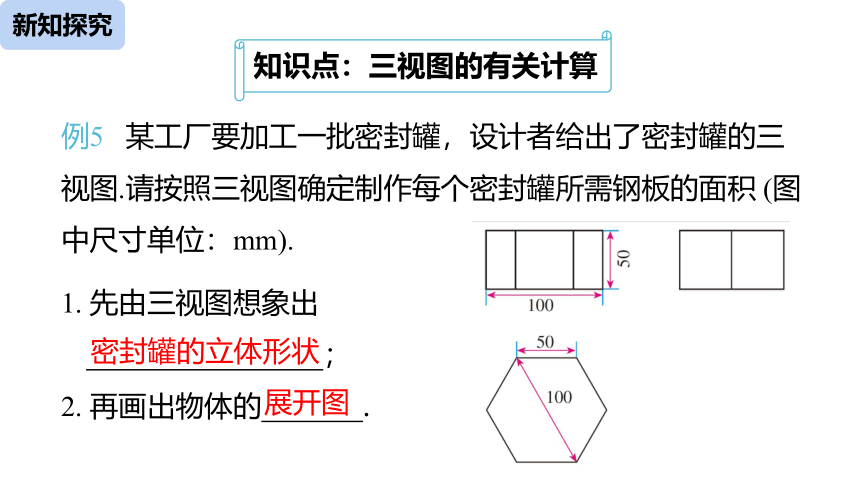
1. 先由三视图想象出
;
2. 再画出物体的 .
密封罐的立体形状
展开图
例5 某工厂要加工一批密封罐,设计者给出了密封罐的三视图.请按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位:mm).
新知探究
解:由三视图可知,密封罐的形状是正六棱柱.
50mm
50mm
密封罐的高为50 mm,底面正六边形的直径为100 mm,边长为50 mm,
100mm
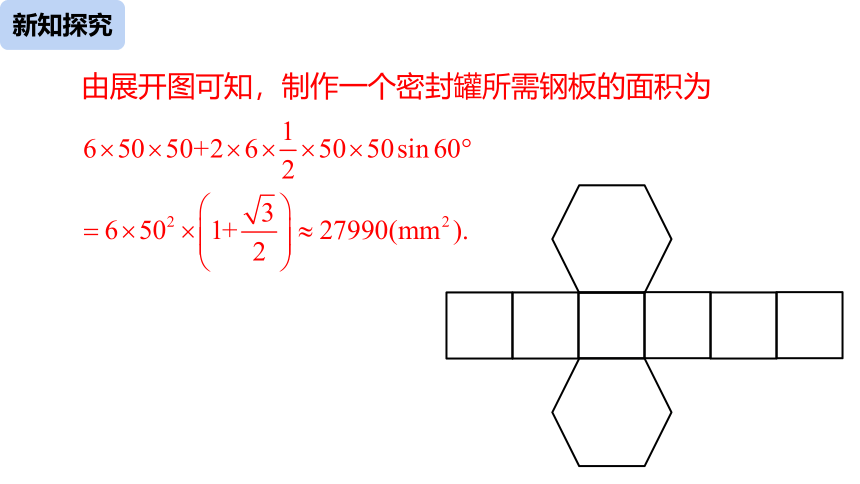
如图,是它的展开图.
新知探究
由展开图可知,制作一个密封罐所需钢板的面积为
新知探究
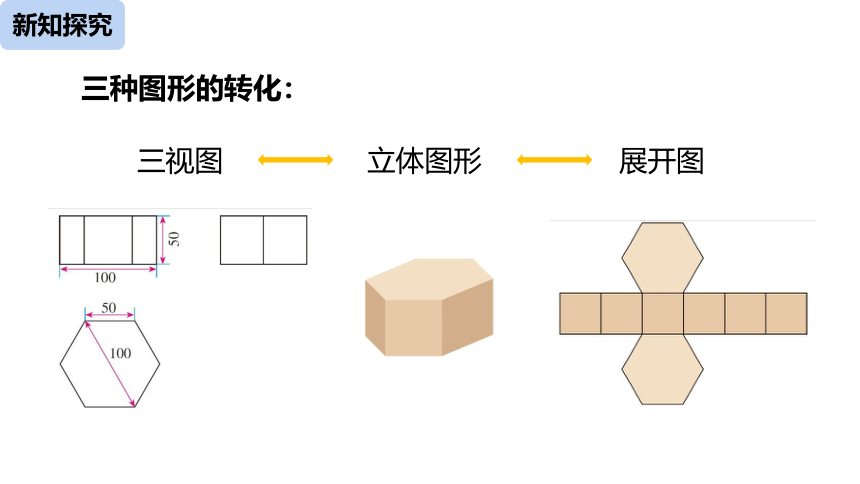
三种图形的转化:
三视图
立体图形
展开图
新知探究
先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.
将立体图形展开成一个平面图形 (展开图),观察它的组成部分.
最后根据已知数据,求出展开图的面积.
由三视图求立体图形面积的方法
1
3
2
新知探究
如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
解:该几何体的上面是底面直径为 20 cm,高为 32 cm 的圆柱,下面是长为 30 cm,宽为 25 cm,高为 40 cm 的长方体.
表面积为:
20×32π+30×40×2+25×40×2+25×30×2=(5900+640π)(cm2).
新知探究
如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
体积为:
25×30×40+102×32π=(30000+3200π)(cm3).
解:该几何体的上面是底面直径为 20 cm,高为 32 cm 的圆柱,下面是长为 30 cm,宽为 25 cm,高为 40 cm 的长方体.
新知探究
先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等;
根据已知数据,结合几何体体积公式求出立体图形的 体积.
由三视图求立体图形体积的方法
1
2
跟踪训练
如图,是一个几何体的三视图,则该几何体的表面积是 .
2 cm
2 cm
3cm
?
解析:该几何体上面是底面直径为2cm,高为3cm的圆锥体,可求出母线为1+(3)2=2cm,
下面是底面边长为2cm,高为2cm的圆柱体,
则该几何体的表面积=S圆柱底面积+S圆柱侧面积+S圆锥侧面积
=π×12+2π×1×2+12×2π×1×2
=π+4π+2π
=7π.
?
跟踪训练
随堂练习
1.如图是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是( )
A.80- 2π B.80+4π
C.80 D.80+6π
本题易忽略长方体内部挖去一个圆柱后形成的表面面积.
随堂练习
解析:由三视图可知,该几何体是长方体中间挖去一个圆柱后的几何体.
其中,长方体的长、宽、高分别为 4,4,3,圆柱的底面直径为 2,高为 3.
则长方体的表面积为 4×4×2+4×3×4=80,
圆柱的侧面积为 2π×3=6π,
上、下底面空心圆面积和为 2π,
故这个几何体的表面积为 80+6π - 2π=80+4π.
随堂练习
2.如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
A.800π+1200
B.160π+1700
C.3200π+1200
D.800π+3000
随堂练习
解析:由三视图可知,该几何体是由一个圆柱和一个长方体组成的,
圆柱底面直径为 20,高为 8,
长方体的长为 30,宽为 20,高为 5,
故该几何体的体积为
π×102×8+30×20×5=800π+3000.
随堂练习
3.在某儿童游乐园门口需要修建一个由正方体和圆柱组合而成的立体图形,如图所示,已知正方体的棱长与圆柱的直径及高相等,都是 1 m.
(1)请画出该立体图形的三视图;
解:(1)该立体图形的三视图如图所示.
随堂练习
(2)为了好看,需要在该立体图形表面刷一层油漆,已知油漆每平方米30元,那么一共需要花费多少元?(结果精确到0.1)
计算该立方体图形的表面积时,要注意圆柱和正方体的重合部分,还有正方体的下底面与地面是重合的,不能计算在内.
解:(2)根据题意得,该立体图形表面需要刷油漆的面积为1×1×5+π×1×1=(5+π)(m2),
则 30×(5+π)≈244.2(元).
答:一共需要花费约244.2元.
(2)为了好看,需要在该立体图形表面刷一层油漆,已知油漆每平方米30元,那么一共需要花费多少元?(结果精确到0.1)
随堂练习
先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.再将立体图形展开成一个平面图形 (展开图),观察它的组成部分.最后根据已知数据,求出展开图的面积.
先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等,再根据已知数据,结合几何体体积公式求出立体图形的体积.
课堂小结
三视图
立体图形
表面积
体积
对接中考
1.(2020·荆门中考)如图是一个几何体的三视图,则该几何体的体积为( )
A.1 B.2
C.2D.4
?
解析:由三视图可知该几何体是底面边为2,高为1的等腰三角形,高为2的直三棱柱,
故该几何体的体积为(1+1)×1÷2×2=2×1÷2×2=2.
B
对接中考
2.(2019·桂林中考)一个物体的三视图如图所示,其中主视图和左视图是全等的等边三角形,俯视图是圆,根据图中所示数据,可求这个物体的表面积为( )
A.π B.2π
C.3πD.( 3 +1)π
?
对接中考
解析:由三视图可知,该几何体是一个圆锥,其轴截面是一个高为 3 的正三角形,
所以正三角形的边长为 3sin60° =2,
所以圆锥的底面圆半径是 1,母线长是 2,
所以底面周长为 2π,侧面积为 12×2π×2 =2π,
又底面积为 πr2=π,
所以表面积是2π+π=3π.
?
对接中考
3.(2018·临沂中考)如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据求得这个几何体的侧面积是( )
A.12 cm2 B. (12+π) cm2
C.6π cm2 D.8π cm2
解析:由三视图确定该几何体是圆柱体,
底面半径是 2÷2=1(cm),高是 3 cm.
所以该几何体的侧面积为 2π×1×3 =6π(cm2).
C
课后作业
请完成课本后习题第10题.
投影与视图
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
如图所示是一个立体图形的三视图.
(1) 请根据视图说出立体图形的名称,并画出它的展开图.
(2) 请指出三视图、立体图形、展开图之间的对应边.
学习目标
1.能熟练地画出物体的三视图和由三视图想象出物体形状,进一步提高空间想象能力.
2.由三视图想象出立体图形后能进行简单的面积或体积的计算.
课堂导入
在实际生活中,我们研究一个几何体通常要知道它的表面积和体积,那么根据几何体的三视图能否求出几何体的表面积和体积呢?本节课我们就来研究根据物体三视图求其展开图形的面积问题.
新知探究
知识点:三视图的有关计算
1. 先由三视图想象出
;
2. 再画出物体的 .
密封罐的立体形状
展开图
例5 某工厂要加工一批密封罐,设计者给出了密封罐的三视图.请按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位:mm).
新知探究
解:由三视图可知,密封罐的形状是正六棱柱.
50mm
50mm
密封罐的高为50 mm,底面正六边形的直径为100 mm,边长为50 mm,
100mm
如图,是它的展开图.
新知探究
由展开图可知,制作一个密封罐所需钢板的面积为
新知探究
三种图形的转化:
三视图
立体图形
展开图
新知探究
先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.
将立体图形展开成一个平面图形 (展开图),观察它的组成部分.
最后根据已知数据,求出展开图的面积.
由三视图求立体图形面积的方法
1
3
2
新知探究
如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
解:该几何体的上面是底面直径为 20 cm,高为 32 cm 的圆柱,下面是长为 30 cm,宽为 25 cm,高为 40 cm 的长方体.
表面积为:
20×32π+30×40×2+25×40×2+25×30×2=(5900+640π)(cm2).
新知探究
如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
体积为:
25×30×40+102×32π=(30000+3200π)(cm3).
解:该几何体的上面是底面直径为 20 cm,高为 32 cm 的圆柱,下面是长为 30 cm,宽为 25 cm,高为 40 cm 的长方体.
新知探究
先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等;
根据已知数据,结合几何体体积公式求出立体图形的 体积.
由三视图求立体图形体积的方法
1
2
跟踪训练
如图,是一个几何体的三视图,则该几何体的表面积是 .
2 cm
2 cm
3cm
?
解析:该几何体上面是底面直径为2cm,高为3cm的圆锥体,可求出母线为1+(3)2=2cm,
下面是底面边长为2cm,高为2cm的圆柱体,
则该几何体的表面积=S圆柱底面积+S圆柱侧面积+S圆锥侧面积
=π×12+2π×1×2+12×2π×1×2
=π+4π+2π
=7π.
?
跟踪训练
随堂练习
1.如图是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是( )
A.80- 2π B.80+4π
C.80 D.80+6π
本题易忽略长方体内部挖去一个圆柱后形成的表面面积.
随堂练习
解析:由三视图可知,该几何体是长方体中间挖去一个圆柱后的几何体.
其中,长方体的长、宽、高分别为 4,4,3,圆柱的底面直径为 2,高为 3.
则长方体的表面积为 4×4×2+4×3×4=80,
圆柱的侧面积为 2π×3=6π,
上、下底面空心圆面积和为 2π,
故这个几何体的表面积为 80+6π - 2π=80+4π.
随堂练习
2.如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
A.800π+1200
B.160π+1700
C.3200π+1200
D.800π+3000
随堂练习
解析:由三视图可知,该几何体是由一个圆柱和一个长方体组成的,
圆柱底面直径为 20,高为 8,
长方体的长为 30,宽为 20,高为 5,
故该几何体的体积为
π×102×8+30×20×5=800π+3000.
随堂练习
3.在某儿童游乐园门口需要修建一个由正方体和圆柱组合而成的立体图形,如图所示,已知正方体的棱长与圆柱的直径及高相等,都是 1 m.
(1)请画出该立体图形的三视图;
解:(1)该立体图形的三视图如图所示.
随堂练习
(2)为了好看,需要在该立体图形表面刷一层油漆,已知油漆每平方米30元,那么一共需要花费多少元?(结果精确到0.1)
计算该立方体图形的表面积时,要注意圆柱和正方体的重合部分,还有正方体的下底面与地面是重合的,不能计算在内.
解:(2)根据题意得,该立体图形表面需要刷油漆的面积为1×1×5+π×1×1=(5+π)(m2),
则 30×(5+π)≈244.2(元).
答:一共需要花费约244.2元.
(2)为了好看,需要在该立体图形表面刷一层油漆,已知油漆每平方米30元,那么一共需要花费多少元?(结果精确到0.1)
随堂练习
先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.再将立体图形展开成一个平面图形 (展开图),观察它的组成部分.最后根据已知数据,求出展开图的面积.
先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高、底面半径等,再根据已知数据,结合几何体体积公式求出立体图形的体积.
课堂小结
三视图
立体图形
表面积
体积
对接中考
1.(2020·荆门中考)如图是一个几何体的三视图,则该几何体的体积为( )
A.1 B.2
C.2D.4
?
解析:由三视图可知该几何体是底面边为2,高为1的等腰三角形,高为2的直三棱柱,
故该几何体的体积为(1+1)×1÷2×2=2×1÷2×2=2.
B
对接中考
2.(2019·桂林中考)一个物体的三视图如图所示,其中主视图和左视图是全等的等边三角形,俯视图是圆,根据图中所示数据,可求这个物体的表面积为( )
A.π B.2π
C.3πD.( 3 +1)π
?
对接中考
解析:由三视图可知,该几何体是一个圆锥,其轴截面是一个高为 3 的正三角形,
所以正三角形的边长为 3sin60° =2,
所以圆锥的底面圆半径是 1,母线长是 2,
所以底面周长为 2π,侧面积为 12×2π×2 =2π,
又底面积为 πr2=π,
所以表面积是2π+π=3π.
?
对接中考
3.(2018·临沂中考)如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据求得这个几何体的侧面积是( )
A.12 cm2 B. (12+π) cm2
C.6π cm2 D.8π cm2
解析:由三视图确定该几何体是圆柱体,
底面半径是 2÷2=1(cm),高是 3 cm.
所以该几何体的侧面积为 2π×1×3 =6π(cm2).
C
课后作业
请完成课本后习题第10题.
