人教版数学九年级下册29.2 三视图 课时3课件(24张)
文档属性
| 名称 | 人教版数学九年级下册29.2 三视图 课时3课件(24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 834.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 23:54:22 | ||
图片预览





文档简介
29.2 三视图
投影与视图
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
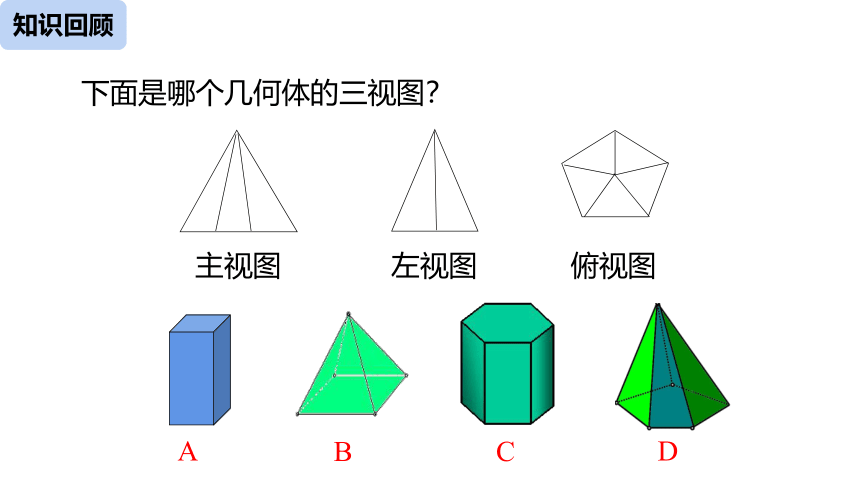
A
C
B
D
下面是哪个几何体的三视图?
主视图 左视图 俯视图
学习目标
1.会根据物体的三视图描述出基本几何体的形状.
2.会根据复杂的三视图判断实物原型.
课堂导入
我们知道,由几何体可以画出三视图,反过来,能否由三视图还原几何体呢?
新知探究
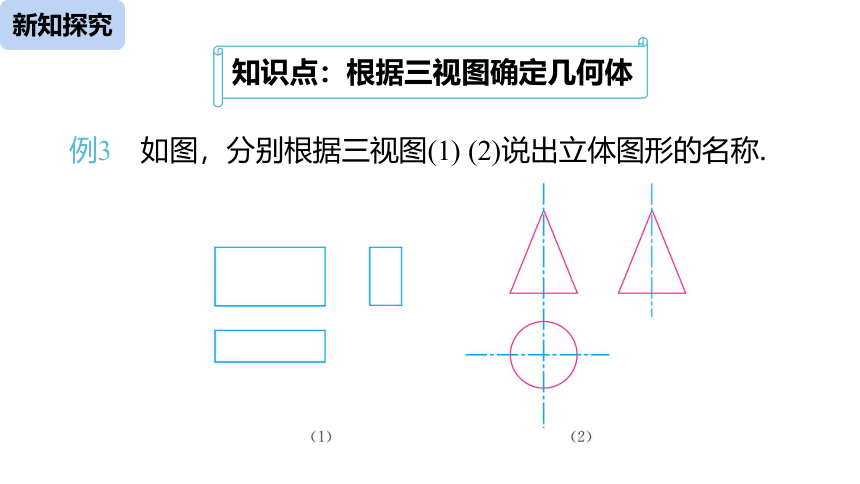
知识点:根据三视图确定几何体
例3 如图,分别根据三视图(1) (2)说出立体图形的名称.
新知探究
(1) 从三个方向看立体图形,视图都是矩形,可以想象这个立体图形是 ,如图(1)所示.
长方体
新知探究
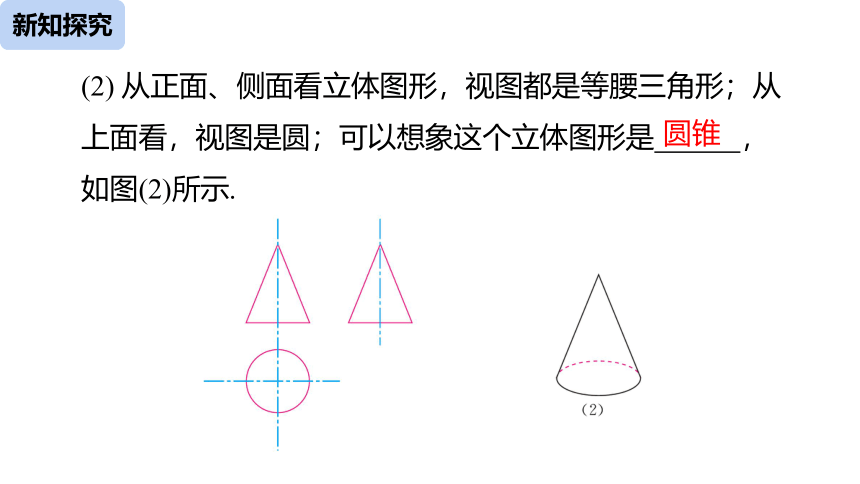
(2) 从正面、侧面看立体图形,视图都是等腰三角形;从上面看,视图是圆;可以想象这个立体图形是 ,如图(2)所示.
圆锥
新知探究
由三视图还原几何体的方法
由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的正面、上面和左面,然后综合起来考虑整体形状.
新知探究
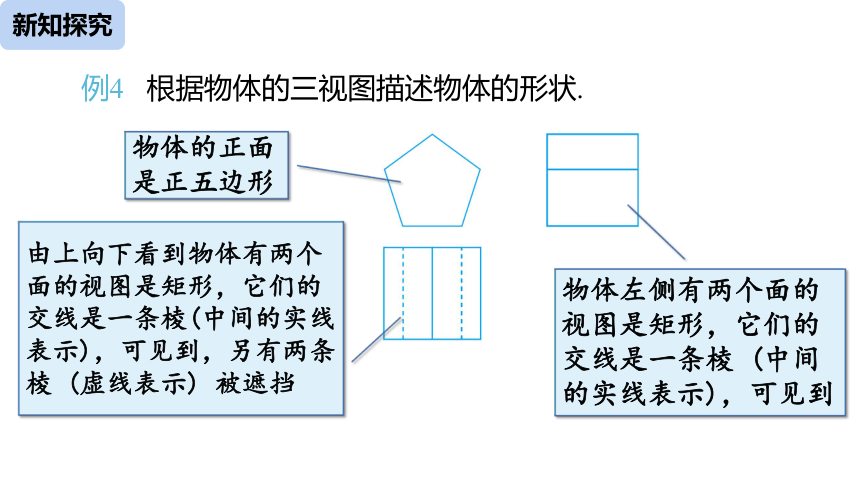
物体的正面是正五边形
由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱(中间的实线表示),可见到,另有两条棱 (虚线表示) 被遮挡
物体左侧有两个面的视图是矩形,它们的交线是一条棱 (中间的实线表示),可见到
例4 根据物体的三视图描述物体的形状.
新知探究
例4 根据物体的三视图描述物体的形状.
物体的形状是正五棱柱,如右图所示.
新知探究
1.根据主视图、俯视图和左视图想象几何体的正面、上面和左面的形状以及几何体的长、宽、高.
2.根据实线和虚线想象几何体看得见和看不见的轮廓线.
3.熟记一些简单几何体的三视图会对复杂几何体的想象有帮助.
4.利用由三视图还原几何体与由几何体画三视图的互逆过程,反复练习,不断总结方法.
由三视图想象几何体形状的常用途径
新知探究
请根据下面提供的三视图,画出几何图形.
(1) 主视图
左视图
俯视图
新知探究
(2) 主视图
左视图
俯视图
请根据下面提供的三视图,画出几何图形.
新知探究
一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性,如正方体的主视图是正方形,但主视图是正方形的几何体可能是直棱柱、长方体、圆柱等.
新知探究
活学巧记
三视图定几何体,主视图想象正面,
俯视图想象上面,左视图想象左面,
综合起来图形现;三视图和几何体,
相互转化可检验.
跟踪训练
根据图中三视图可知该几何体是( )
A.三棱锥
B.三棱柱
C.四棱锥
D.四棱柱
柱体
三棱柱
B
随堂练习
1.如图所示的三视图表示的几何体是( )
A
B
C
D
A
主视图
左视图
俯视图
随堂练习
2.如图,是一个几何体的主视图和左视图,则这个几何体可能为( )
B
A
C
D
两矩形的宽一致
矩形中间有一条实线
矩形中间有一条虚线
B
主视图
左视图
随堂练习
3.如图,是一个几何体的三视图,则这个几何体是( )
A
B
C
D
上方是圆锥体
下方是长方体
B
课堂小结
由三视图确定几何体
由三视图确定简单几何体
由三视图确定复杂几何体
由三视图确定简单几何体的组合体
对接中考
1.(2020·宜昌中考)诗句“横看成岭侧成峰,远近高低各不同”,意思是说要认清事物的本质,就必须从不同角度去观察.如图是对某物体从不同角度观察的记录情况,对该物体的判断最接近本质的是( )
A.是圆柱形物体和球形物体的组合体,里面有两个垂直的空心管
B.是圆柱形物体和球形物体的组合体,里面有两个平行的空心管
C.是圆柱形物体,里面有两个垂直的空心管
D.是圆柱形物体,里面有两个平行的空心管
D
对接中考
2.(2020·鄂尔多斯中考)已知某物体的三视图如图所示,那么与它对应的物体是( )
C
上方是圆柱体
下方是长方体
长方体的宽与圆柱底面的直径相等
对接中考
3.(2020·雅安中考)一个几何体由若干大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为( )
A.4 B.5 C.6 D.7
1
B
至少有一处为2个
1
1
2
课后作业
请完成课本后习题第4题.
投影与视图
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
知识回顾
A
C
B
D
下面是哪个几何体的三视图?
主视图 左视图 俯视图
学习目标
1.会根据物体的三视图描述出基本几何体的形状.
2.会根据复杂的三视图判断实物原型.
课堂导入
我们知道,由几何体可以画出三视图,反过来,能否由三视图还原几何体呢?
新知探究
知识点:根据三视图确定几何体
例3 如图,分别根据三视图(1) (2)说出立体图形的名称.
新知探究
(1) 从三个方向看立体图形,视图都是矩形,可以想象这个立体图形是 ,如图(1)所示.
长方体
新知探究
(2) 从正面、侧面看立体图形,视图都是等腰三角形;从上面看,视图是圆;可以想象这个立体图形是 ,如图(2)所示.
圆锥
新知探究
由三视图还原几何体的方法
由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的正面、上面和左面,然后综合起来考虑整体形状.
新知探究
物体的正面是正五边形
由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱(中间的实线表示),可见到,另有两条棱 (虚线表示) 被遮挡
物体左侧有两个面的视图是矩形,它们的交线是一条棱 (中间的实线表示),可见到
例4 根据物体的三视图描述物体的形状.
新知探究
例4 根据物体的三视图描述物体的形状.
物体的形状是正五棱柱,如右图所示.
新知探究
1.根据主视图、俯视图和左视图想象几何体的正面、上面和左面的形状以及几何体的长、宽、高.
2.根据实线和虚线想象几何体看得见和看不见的轮廓线.
3.熟记一些简单几何体的三视图会对复杂几何体的想象有帮助.
4.利用由三视图还原几何体与由几何体画三视图的互逆过程,反复练习,不断总结方法.
由三视图想象几何体形状的常用途径
新知探究
请根据下面提供的三视图,画出几何图形.
(1) 主视图
左视图
俯视图
新知探究
(2) 主视图
左视图
俯视图
请根据下面提供的三视图,画出几何图形.
新知探究
一个摆好的几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性,如正方体的主视图是正方形,但主视图是正方形的几何体可能是直棱柱、长方体、圆柱等.
新知探究
活学巧记
三视图定几何体,主视图想象正面,
俯视图想象上面,左视图想象左面,
综合起来图形现;三视图和几何体,
相互转化可检验.
跟踪训练
根据图中三视图可知该几何体是( )
A.三棱锥
B.三棱柱
C.四棱锥
D.四棱柱
柱体
三棱柱
B
随堂练习
1.如图所示的三视图表示的几何体是( )
A
B
C
D
A
主视图
左视图
俯视图
随堂练习
2.如图,是一个几何体的主视图和左视图,则这个几何体可能为( )
B
A
C
D
两矩形的宽一致
矩形中间有一条实线
矩形中间有一条虚线
B
主视图
左视图
随堂练习
3.如图,是一个几何体的三视图,则这个几何体是( )
A
B
C
D
上方是圆锥体
下方是长方体
B
课堂小结
由三视图确定几何体
由三视图确定简单几何体
由三视图确定复杂几何体
由三视图确定简单几何体的组合体
对接中考
1.(2020·宜昌中考)诗句“横看成岭侧成峰,远近高低各不同”,意思是说要认清事物的本质,就必须从不同角度去观察.如图是对某物体从不同角度观察的记录情况,对该物体的判断最接近本质的是( )
A.是圆柱形物体和球形物体的组合体,里面有两个垂直的空心管
B.是圆柱形物体和球形物体的组合体,里面有两个平行的空心管
C.是圆柱形物体,里面有两个垂直的空心管
D.是圆柱形物体,里面有两个平行的空心管
D
对接中考
2.(2020·鄂尔多斯中考)已知某物体的三视图如图所示,那么与它对应的物体是( )
C
上方是圆柱体
下方是长方体
长方体的宽与圆柱底面的直径相等
对接中考
3.(2020·雅安中考)一个几何体由若干大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为( )
A.4 B.5 C.6 D.7
1
B
至少有一处为2个
1
1
2
课后作业
请完成课本后习题第4题.
