人教版数学九年级下册29.3 课题学习 制作立体模型 课时1课件(24张)
文档属性
| 名称 | 人教版数学九年级下册29.3 课题学习 制作立体模型 课时1课件(24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1000.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 23:54:57 | ||
图片预览







文档简介
投影与视图
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
29.3 课题学习 制作立体模型
知识回顾
如图,根据三视图描述物体的形状.
学习目标
1.通过根据三视图制作立体模型的实践活动,体验平面图形向立体图形转化的过程,体会用三视图表示立体图形的作用.
2.进一步感受立体图形与平面图形之间的联系.
课堂导入
观察下面的玩具模型,它们是如何得到的呢?
课堂导入
观察三视图,并综合考虑各视图表达的含义以及视图间的联系,可以想象出三视图所表示的立体图形的形状,这是由视图转化为立体图形的过程. 这节课我们通过动手实践,来体会这个过程.
新知探究
知识点:根据三视图制作立体模型
一、课题学习目的
通过由三视图制作立体模型的实践活动,体验平面图形向立体图形转化的过程,体会用三视图表示立体图形的作用,进一步感受立体图形与平面图形之间的联系.
新知探究
二、工具准备
刻度尺、剪刀、小刀、胶水、硬纸板、马铃薯(或萝卜)等.
新知探究
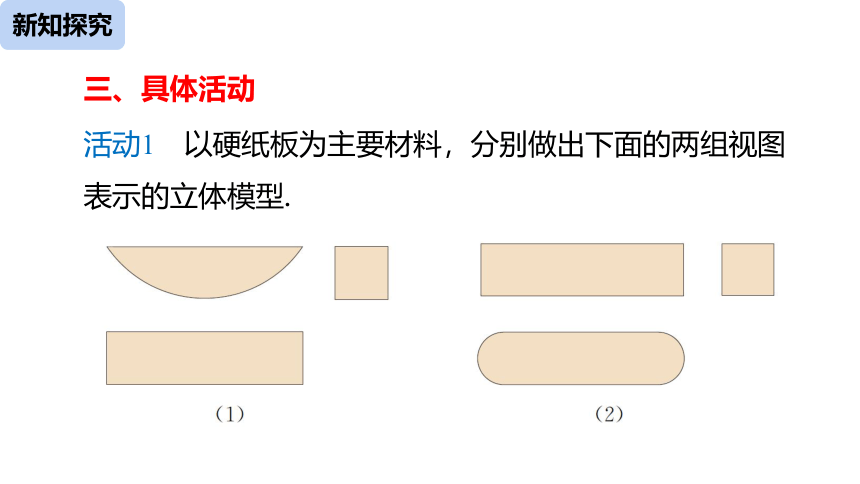
活动1 以硬纸板为主要材料,分别做出下面的两组视图表示的立体模型.
三、具体活动
新知探究
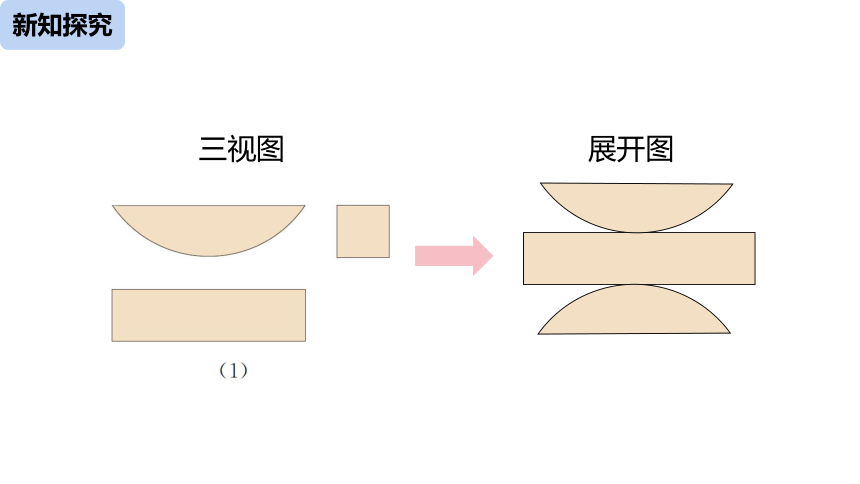
三视图
展开图
新知探究
三视图
展开图
新知探究
根据三视图制作立体模型,需要先由三视图想出立体图形,再画出平面展开图并折合展开图为立体图形或先分别画出立体图形的各个侧面,再将它们黏合起来.
新知探究
活动2 按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型.
圆锥
由三视图想出立体图形,将想出来的立体图形直接刻制出来.
新知探究
底面为五边形的直五棱柱,底面五边形有三个直角.
活动2 按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型.
跟踪训练
某几何体的三视图如图所示,则这个几何体是( )
A
随堂练习
主视图
左视图
俯视图
1.请根据下面提供的三视图,画出几何图形.
随堂练习
1.请根据下面提供的三视图,画出几何图形.
主视图
左视图
俯视图
随堂练习
2.一个几何体的主视图和左视图如图所示,请补画出这个几何体的俯视图.
左视图
主视图
随堂练习
3.如图是一个上下底密封的纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积.(结果可保留根号)
随堂练习
解:根据该几何体的三视图可知其是一个六棱柱,
∵其高为12cm,底面半径为5 cm,
∴其侧面积为6×5×12=360cm2,
底面积为12×5×32×5×12?=753??cm2,
∴其表面积为(753?+360)cm2.
?
课堂小结
三视图
立体模型
立体图形
想象
刻制
立体图形
想象
展开图
画出
折合
对接中考
1.(2020·随州中考)一个几何体的三视图如图所示,则该几何体为( )
A.圆柱
B.圆锥
C.四棱柱
D.四棱锥
A
对接中考
2.(2020·呼和浩特中考)一个几何体的三视图如图所示,则该几何体的表面积为 .
解析:观察该几何体的三视图发现其为半个圆柱,
半圆柱的直径为 2,高为 2,
故其表面积为 π×12+(π+2)×2=3π+4.
3π+4
2
2
主视图
左视图
俯视图
1
对接中考
3.(2020·宁夏中考)如图 2 是图 1 长方体的三视图,若用 S 表示面积,S主=a2,S左=a2+a,则S俯=( )
A.a2+a B.2a2
C.a2+2a+1 D.2a2+a
解:∵ S主=a2=a·a,S左=a2+a=a(a+1),
∴ 俯视图的长为 a+1,宽为 a,
∴ S俯=a·(a+1)=a2+a.
A
课后作业
请完成课本后习题第6题.
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
29.3 课题学习 制作立体模型
知识回顾
如图,根据三视图描述物体的形状.
学习目标
1.通过根据三视图制作立体模型的实践活动,体验平面图形向立体图形转化的过程,体会用三视图表示立体图形的作用.
2.进一步感受立体图形与平面图形之间的联系.
课堂导入
观察下面的玩具模型,它们是如何得到的呢?
课堂导入
观察三视图,并综合考虑各视图表达的含义以及视图间的联系,可以想象出三视图所表示的立体图形的形状,这是由视图转化为立体图形的过程. 这节课我们通过动手实践,来体会这个过程.
新知探究
知识点:根据三视图制作立体模型
一、课题学习目的
通过由三视图制作立体模型的实践活动,体验平面图形向立体图形转化的过程,体会用三视图表示立体图形的作用,进一步感受立体图形与平面图形之间的联系.
新知探究
二、工具准备
刻度尺、剪刀、小刀、胶水、硬纸板、马铃薯(或萝卜)等.
新知探究
活动1 以硬纸板为主要材料,分别做出下面的两组视图表示的立体模型.
三、具体活动
新知探究
三视图
展开图
新知探究
三视图
展开图
新知探究
根据三视图制作立体模型,需要先由三视图想出立体图形,再画出平面展开图并折合展开图为立体图形或先分别画出立体图形的各个侧面,再将它们黏合起来.
新知探究
活动2 按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型.
圆锥
由三视图想出立体图形,将想出来的立体图形直接刻制出来.
新知探究
底面为五边形的直五棱柱,底面五边形有三个直角.
活动2 按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型.
跟踪训练
某几何体的三视图如图所示,则这个几何体是( )
A
随堂练习
主视图
左视图
俯视图
1.请根据下面提供的三视图,画出几何图形.
随堂练习
1.请根据下面提供的三视图,画出几何图形.
主视图
左视图
俯视图
随堂练习
2.一个几何体的主视图和左视图如图所示,请补画出这个几何体的俯视图.
左视图
主视图
随堂练习
3.如图是一个上下底密封的纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积.(结果可保留根号)
随堂练习
解:根据该几何体的三视图可知其是一个六棱柱,
∵其高为12cm,底面半径为5 cm,
∴其侧面积为6×5×12=360cm2,
底面积为12×5×32×5×12?=753??cm2,
∴其表面积为(753?+360)cm2.
?
课堂小结
三视图
立体模型
立体图形
想象
刻制
立体图形
想象
展开图
画出
折合
对接中考
1.(2020·随州中考)一个几何体的三视图如图所示,则该几何体为( )
A.圆柱
B.圆锥
C.四棱柱
D.四棱锥
A
对接中考
2.(2020·呼和浩特中考)一个几何体的三视图如图所示,则该几何体的表面积为 .
解析:观察该几何体的三视图发现其为半个圆柱,
半圆柱的直径为 2,高为 2,
故其表面积为 π×12+(π+2)×2=3π+4.
3π+4
2
2
主视图
左视图
俯视图
1
对接中考
3.(2020·宁夏中考)如图 2 是图 1 长方体的三视图,若用 S 表示面积,S主=a2,S左=a2+a,则S俯=( )
A.a2+a B.2a2
C.a2+2a+1 D.2a2+a
解:∵ S主=a2=a·a,S左=a2+a=a(a+1),
∴ 俯视图的长为 a+1,宽为 a,
∴ S俯=a·(a+1)=a2+a.
A
课后作业
请完成课本后习题第6题.
