人教版数学九年级下册29.3 课题学习 制作立体模型 课时2课件(21张)
文档属性
| 名称 | 人教版数学九年级下册29.3 课题学习 制作立体模型 课时2课件(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 611.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 00:00:00 | ||
图片预览



文档简介
投影与视图
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
29.3 课题学习 制作立体模型
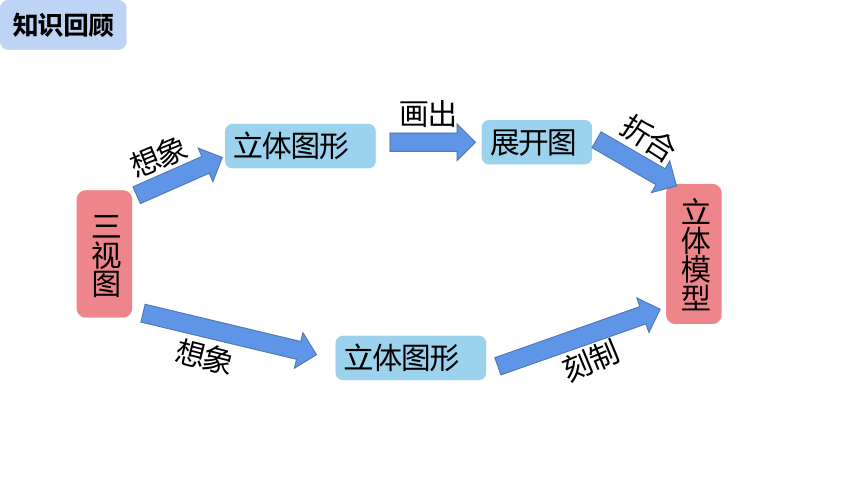
知识回顾
三视图
立体模型
立体图形
想象
刻制
立体图形
想象
展开图
画出
折合
学习目标
1.通过根据展开图制作立体模型的实践活动,体验平面图形向立体图形转化的过程,体会展开图与立体图形的关系.
2.进一步感受立体图形与平面图形之间的联系.
课堂导入
与几何体相关的平面图形包括三视图和展开图,上节课我们知道由三视图可以得到几何体,那么由展开图怎样得到几何体呢? 这节课我们将通过动手实践,来体会这个过程.
新知探究
知识点:根据展开图制作立体模型
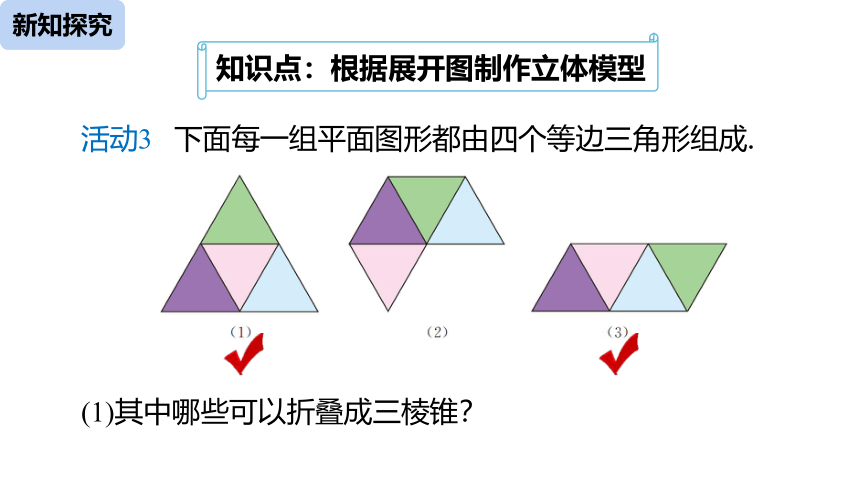
活动3 下面每一组平面图形都由四个等边三角形组成.
(1)其中哪些可以折叠成三棱锥?
新知探究
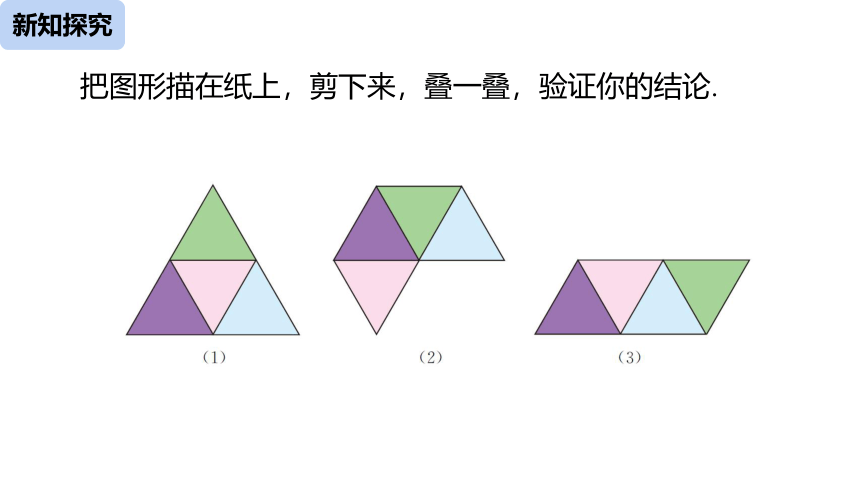
把图形描在纸上,剪下来,叠一叠,验证你的结论.
新知探究
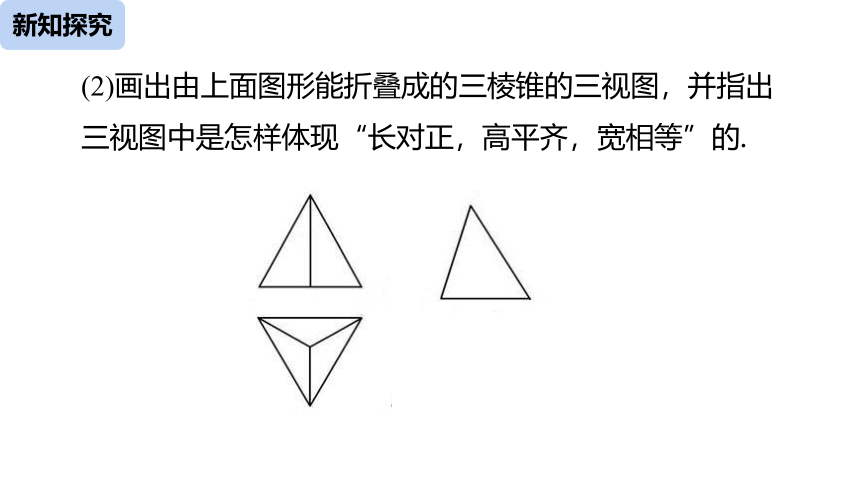
(2)画出由上面图形能折叠成的三棱锥的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的.
新知探究
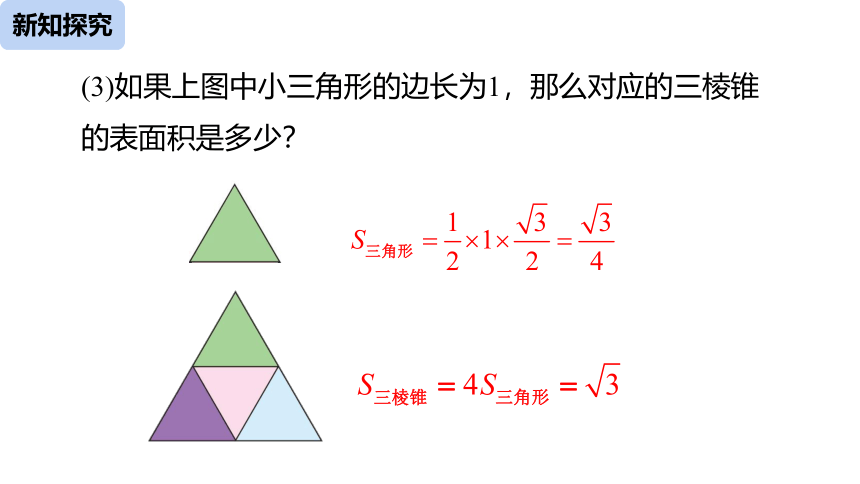
(3)如果上图中小三角形的边长为1,那么对应的三棱锥的表面积是多少?
新知探究
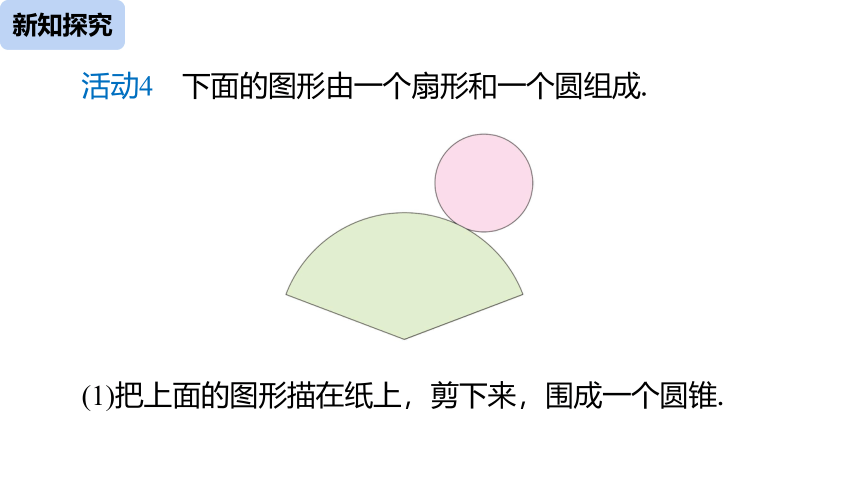
活动4 下面的图形由一个扇形和一个圆组成.
(1)把上面的图形描在纸上,剪下来,围成一个圆锥.
新知探究
(2)画出由上面图形围成的圆锥的三视图.
(3)如果图中扇形的半径为13,圆的半径为5,那么对应的圆锥的体积是多少?
13
12
5
V= 13×π×????2×h
= 13×π×52×12
= 100π .
?
新知探究
跟踪训练
一个几何体的表面展开图如图所示,这个几何体是( )
A.正方体
B.三棱锥
C.四棱锥
D.圆柱
D
随堂练习
1.下列平面展开图是由5个大小相同的正方形组成的,其中沿正方形的边不能折成无盖小方盒的是( )
B
A B C D
随堂练习
2.如图是某几何体的平面展开图,求图中小圆的半径.
解:
随堂练习
3.如图,长方体长为4 cm,宽为2 cm,高为5 cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,求蚂蚁爬行的最短路径长.
随堂练习
解:作出这个长方体的侧面展开图,则最短路径如图为PQ.
课堂小结
三种图形的转化:
三视图
立体图形
展开图
对接中考
1.(2020·衡阳中考)下列不是三棱柱展开图的是( )
A
B
C
D
两个三角形重合为同一底面,而另一底面没有
B
对接中考
2.(2020·永州中考)如图,这是一个底面为等边三角形的正三棱柱和它的主视图、俯视图,则它的左视图的面积是( )
A.4 B.2 C.3 D.23
?
左视图为矩形
高平齐→矩形长为2
宽相等→矩形宽为????
?
2
D
对接中考
3.(2019·大庆中考)一个“粮仓”的三视图如图所示(单位:m),则它的体积是( )
A.21π m3 B.30π m3
C.45π m3 D.63π m3
解析:观察发现该几何体为圆锥和圆柱
的结合体,其体积为:32π×4+13×32π×3=45πm3.
?
C
课后作业
写一篇短文介绍三视图、展开图的应用,以及你的感受.
人教版-数学-九年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-对接中考
29.3 课题学习 制作立体模型
知识回顾
三视图
立体模型
立体图形
想象
刻制
立体图形
想象
展开图
画出
折合
学习目标
1.通过根据展开图制作立体模型的实践活动,体验平面图形向立体图形转化的过程,体会展开图与立体图形的关系.
2.进一步感受立体图形与平面图形之间的联系.
课堂导入
与几何体相关的平面图形包括三视图和展开图,上节课我们知道由三视图可以得到几何体,那么由展开图怎样得到几何体呢? 这节课我们将通过动手实践,来体会这个过程.
新知探究
知识点:根据展开图制作立体模型
活动3 下面每一组平面图形都由四个等边三角形组成.
(1)其中哪些可以折叠成三棱锥?
新知探究
把图形描在纸上,剪下来,叠一叠,验证你的结论.
新知探究
(2)画出由上面图形能折叠成的三棱锥的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的.
新知探究
(3)如果上图中小三角形的边长为1,那么对应的三棱锥的表面积是多少?
新知探究
活动4 下面的图形由一个扇形和一个圆组成.
(1)把上面的图形描在纸上,剪下来,围成一个圆锥.
新知探究
(2)画出由上面图形围成的圆锥的三视图.
(3)如果图中扇形的半径为13,圆的半径为5,那么对应的圆锥的体积是多少?
13
12
5
V= 13×π×????2×h
= 13×π×52×12
= 100π .
?
新知探究
跟踪训练
一个几何体的表面展开图如图所示,这个几何体是( )
A.正方体
B.三棱锥
C.四棱锥
D.圆柱
D
随堂练习
1.下列平面展开图是由5个大小相同的正方形组成的,其中沿正方形的边不能折成无盖小方盒的是( )
B
A B C D
随堂练习
2.如图是某几何体的平面展开图,求图中小圆的半径.
解:
随堂练习
3.如图,长方体长为4 cm,宽为2 cm,高为5 cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,求蚂蚁爬行的最短路径长.
随堂练习
解:作出这个长方体的侧面展开图,则最短路径如图为PQ.
课堂小结
三种图形的转化:
三视图
立体图形
展开图
对接中考
1.(2020·衡阳中考)下列不是三棱柱展开图的是( )
A
B
C
D
两个三角形重合为同一底面,而另一底面没有
B
对接中考
2.(2020·永州中考)如图,这是一个底面为等边三角形的正三棱柱和它的主视图、俯视图,则它的左视图的面积是( )
A.4 B.2 C.3 D.23
?
左视图为矩形
高平齐→矩形长为2
宽相等→矩形宽为????
?
2
D
对接中考
3.(2019·大庆中考)一个“粮仓”的三视图如图所示(单位:m),则它的体积是( )
A.21π m3 B.30π m3
C.45π m3 D.63π m3
解析:观察发现该几何体为圆锥和圆柱
的结合体,其体积为:32π×4+13×32π×3=45πm3.
?
C
课后作业
写一篇短文介绍三视图、展开图的应用,以及你的感受.
