北师大版九年级上册数学 第3章概率的进一步认识 单元测试(Word版 含答案)
文档属性
| 名称 | 北师大版九年级上册数学 第3章概率的进一步认识 单元测试(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 162.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-27 23:31:19 | ||
图片预览




文档简介
第3章
概率的进一步认识
单元测试
一.选择题
1.不透明布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出一个球,两次都摸出白球的概率是( )
A.
B.
C.
D.
2.如图是两个可以自由转动的转盘,其中一个转盘平均分为4份,另一个转盘平均分为3份,两个转盘分别标有数字;同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为5的概率是( )
A.
B.
C.
D.
3.从分别写有数字1,2,3,4,5的5张卡片中任意取出两张,把第一张卡片上的数字作为十位数字,第二张卡片上的数字作为个位数字,组成一个两位数,则所组成的数是5的倍数的概率是( )
A.
B.
C.
D.
4.在一个口袋中有5个完全相同的小球,把它们分别标号为1,2,3,4,5,随机摸出一个小球不放回,再随机摸出一个小球,则两次摸出小球的标号之和能被3整除的概率是( )
A.
B.
C.
D.
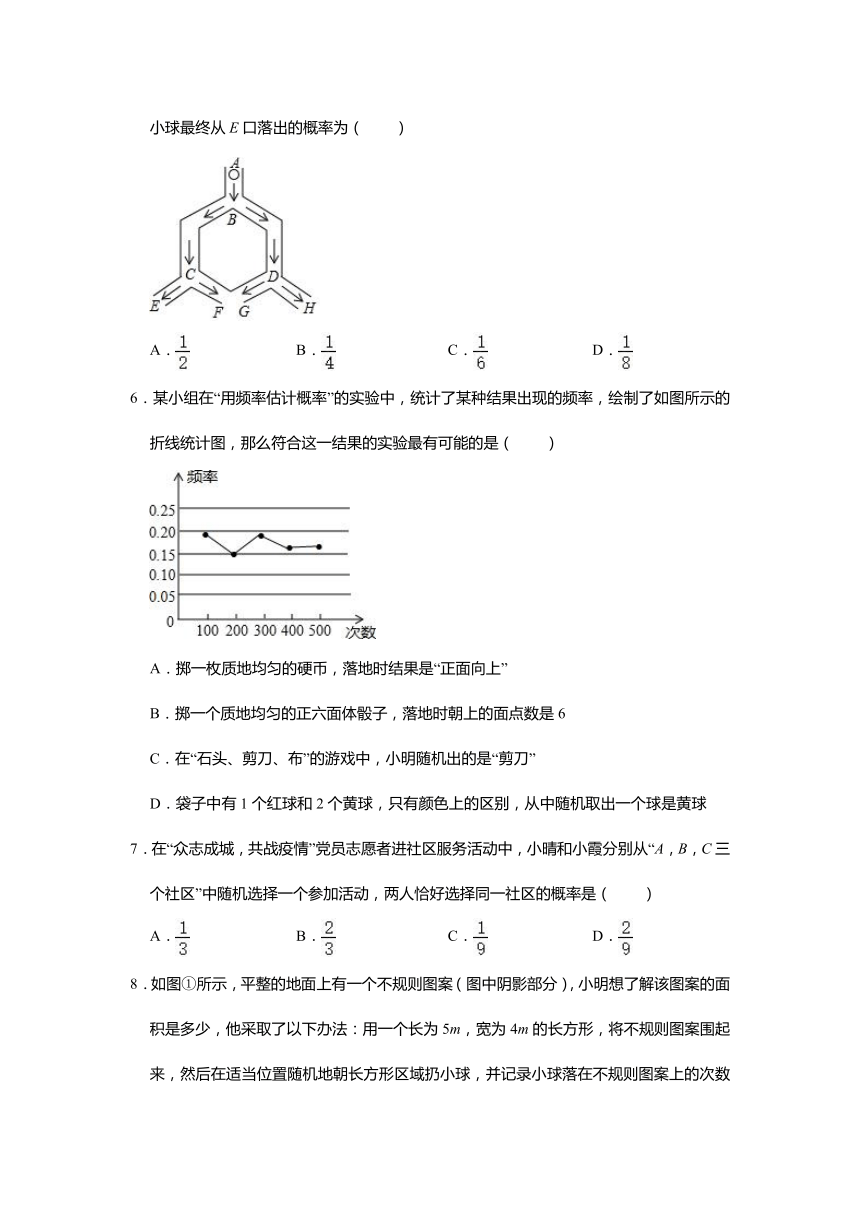
5.如图,小球从A口往下落,在每个交又口都有向左或向右两种可能,且可能性相同,则小球最终从E口落出的概率为( )
A.
B.
C.
D.
6.某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )
A.掷一枚质地均匀的硬币,落地时结果是“正面向上”
B.掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6
C.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D.袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球
7.在“众志成城,共战疫情”党员志愿者进社区服务活动中,小晴和小霞分别从“A,B,C三个社区”中随机选择一个参加活动,两人恰好选择同一社区的概率是( )
A.
B.
C.
D.
8.如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5m,宽为4m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了②所示的折线统计图,由此他估计不规则图案的面积大约为( )
A.6m2
B.7m2
C.8m2
D.9m2
9.从长度分别为1cm、3cm、5cm、6cm四条线段中随机取出三条,则能够组成三角形的概率为( )
A.
B.
C.
D.
10.下列事件的概率,与“任意选2个人,恰好同月过生日”这一事件的概率相等的是( )
A.任意选2个人,恰好生肖相同
B.任意选2个人,恰好同一天过生日
C.任意掷2枚骰子,恰好朝上的点数相同
D.任意掷2枚硬币,恰好朝上的一面相同
二.填空题
11.不透明的袋子中装有红、蓝小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到相同颜色的小球的概率是
.
12.技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为
.(结果要求保留两位小数)
13.某校开展以“我和我的祖国”为主题的“大合唱”活动,七年级准备从小明、小东、小聪三名男生和小红、小慧两名女生中各随机选出一名男生和一名女生担任领唱,则小聪和小慧被同时选中的概率是
.
14.在“抛掷正六面体”的试验中,正六面体的六个面分别标有数字“1”“2”“3”“4”“5”“6”,在试验次数很大时,数字“6”朝上的频率的变化趋势接近的值是
.
15.要考察某运动员罚篮命中率,下表是在多次测试中的统计数据:
罚进个数
80
140
293
523
613
823
罚球总数
110
182
396
701
820
1098
估计该运动员罚篮命中的概率是
.(结果精确到0.01)
16.在一个不透明的袋子中装有3个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.7附近,则袋子中红球约有
个.
17.现有5张正面分别标有数字﹣3,﹣1,1,2,4的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为m,n.则一次函数y=mx+n经过第一、二、四象限的概率是
.
18.2019年12月,湖北省武汉市出现多起病毒性肺炎病例,2020年1月20日,习近平总书记对新型冠状病毒感染的肺炎疫情作出重要指示,强调要把人民群众生命安全和身体健康放在第一位,坚决遏制疫情蔓延势头.全国各地的医护人员积极报名参与抗疫第一线的支援工作.重庆市某医院准备从报名的甲、乙、丙、丁四名医生中随机选择2人去支援湖北,那么乙、丙两人中至少有一人被选中的概率为
.
三.解答题
19.从2021年起,江苏省高考采用“3+1+2”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选1科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
(1)若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是
;
(2)若小明在“1”中选择了物理,用画树状图的方法求他在“2”中选化学、生物的概率.
20.在1、2、3、4这四个数中,先任意取一个数a,然后在余下的数中任意取出一个数b,组成一个点(a,b).求组成的点(a,b)恰好横坐标为偶数且纵坐标为奇数的概率(请用“画树状图”或“列表”等方法写出分析过程).
21.某校开展征文活动,征文主题只能从“爱国”、“敬业”、“诚信”、“友善”四个主题中选择一个,每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.
(1)将上面的条形统计图补充完整;
(2)在扇形统计图中,选择“爱国”主题所对应的圆心角是
°.
(3)如果该校七年级共有1200名考生,请估计选择以“友善”为主题的七年级学生有
名:
(4)学生会宣传部有七年级的2名男生和2名女生,现从中随机挑选2名同学参加“主题征文”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
22.为落实我市关于开展中小学课后服务工作的要求,某学校开设了四门校本课程供学生选择:A.趣味数学;B.博乐阅读;C.快乐英语;D.硬笔书法.某年级共有100名学生选择了A课程,为了解本年级选择A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试,将他们的成绩(百分制)分成六组,绘制成频数分布直方图.
(1)已知70≤x<80这组的数据为:72,73,74,75,76,76,79.则这组数据的中位数是
;众数是
;
(2)根据题中信息,估计该年级选择A课程学生成绩在80≤x<90的总人数;
(3)该年级学生小乔随机选取了一门课程,则小乔选中课程D的概率是
;
(4)该年级每名学生选两门不同的课程,小张和小王在选课程的过程中,若第一次都选了课程C,那么他俩第二次同时选择课程A或课程B的概率是多少?请用列表法或树状图的方法加以说明.
23.实际问题:
某商场为鼓励消费,设计了抽奖活动,方案如下:根据不同的消费金额,每次抽奖时可以从100张面值分别为1元、2元、3元、…、100元的奖券中(面值为整数),一次任意抽取2张、3张、4张、…等若干张奖券,奖券的面值金额之和即为优惠金额.某顾客获得了一次抽取5张奖券的机会,小明想知道该顾客共有多少种不同的优惠金额?
问题建模:
从1,2,3,…,n(n为整数,且n≥3)这n个整数中任取a
(1<a<n)个整数,这a个整数之和共有多少种不同的结果?
模型探究:
我们采取一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,从中找出解决问题的方法.
探究一:
(1)从1,2,3这3个整数中任取2个整数,这2个整数之和共有多少种不同的结果?
表①
所取的2个整数
1,2
1,3
2,3
2个整数之和
3
4
5
如表①,所取的2个整数之和可以为3,4,5,也就是从3到5的连续整数,其中最小是3,最大是5,所以共有3种不同的结果.
(2)从1,2,3,4这4个整数中任取2个整数,这2个整数之和共有多少种不同的结果?
表②
所取的2个整数
1,2
1,3
1,4
2,3
2,4
3,4
2个整数之和
3
4
5
5
6
7
如表②,所取的2个整数之和可以为3,4,5,6,7,也就是从3到7的连续整数,其中最小是3,最大是7,所以共有5种不同的结果.
(3)从1,2,3,4,5这5个整数中任取2个整数,这2个整数之和共有
种不同的结果.
(4)从1,2,3,…,n(n为整数,且n≥3)这n个整数中任取2个整数,这2个整数之和共有
种不同的结果.
探究二:
(1)从1,2,3,4这4个整数中任取3个整数,这3个整数之和共有
种不同的结果.
(2)从1,2,3,…,n(n为整数,且n≥4)这n个整数中任取3个整数,这3个整数之和共有
种不同的结果.
探究三:
从1,2,3,…,n(n为整数,且n≥5)这n个整数中任取4个整数,这4个整数之和共有
种不同的结果.
归纳结论:
从1,2,3,…,n(n为整数,且n≥3)这n个整数中任取a(1<a<n)个整数,这a个整数之和共有
种不同的结果.
问题解决:
从100张面值分别为1元、2元、3元、…、100元的奖券中(面值为整数),一次任意抽取5张奖券,共有
种不同的优惠金额.
拓展延伸:
(1)从1,2,3,…,36这36个整数中任取多少个整数,使得取出的这些整数之和共有204种不同的结果?(写出解答过程)
(2)从3,4,5,…,n+3(n为整数,且n≥2)这(n+1)个整数中任取a(1<a<n+1)个整数,这a个整数之和共有
种不同的结果.
参考答案
1.A.
2.C.
3.C
4.B
5.B
6.B
7.A
8.B
9.A
10.A
11..
12.0.99
13.
14.
15.0.75
16.7
17.:
18.
19.解:(1)在“2”中已选择了地理,从剩下的化学、生物,思想品德三科中选一科,因此选择生物的概率为;
答案为:;
(2)用树状图表示所有可能出现的结果如下:
共有12种可能出现的结果,其中选中“化学”“生物”的有2种,
∴P(化学生物)==.
20.解:画树状图为:
共有12种等可能的结果数,其中组成的点(a,b)恰好横坐标为偶数且纵坐标为奇数的结果数为4,
所以组成的点(a,b)恰好横坐标为偶数且纵坐标为奇数的概率==.
21.解:(1)调查的总人数为3÷6%=50(人),
所以以“友善”为主题的人数为50×30%=15(人),
条形统计图补充为:
(2)在扇形统计图中,选择“爱国”主题所对应的圆心角的度数为360°×=144°;
(3)1200×30%=360,
所以估计选择以“友善”为主题的七年级学生有360名;
答案为144,360;
(4)画树状图为:
共有12种等可能的结果数,其中“1男1女”的结果数为8,
所以恰好选中“1男1女”的概率==.
22.解:(1)在72,73,74,75,76,76,79这组已经按从小到大排列好的数据中,中位数为75,众数为76;
故答案为:75,76;
(2)观察直方图,抽取的30名学生成绩在80≤x<90范围内选取A课程的有9人,所占比为,
那么估计该年级100名学生,学生成绩在80≤x<90范围内,选取A课程的总人数为(人);
(3)因为学校开设了四门校本课程供学生选择,小乔随机选取一门课程,则他选中课程D的概率为;
故答案为:;
(4)因该年级每名学生选两门不同的课程,第一次都选了课程C,列树状图如下:
等可能结果共有9种,他俩第二次同时选择课程A或课程B的有2种,
所以,他俩第二次同时选择课程A或课程B的概率是.
23.解:探究一:
(3)从1,2,3,4,5这5个整数中任取2个整数,这2个整数之和最小值为1+2=3,最大值为4+5=9,这2个整数之和共有9﹣3+1=7种不同情况;
故答案为:7;
(4)从1,2,3,…,n(n为整数,且n≥3)这n个整数中任取2个整数,这2个整数之和最小值为1+2=3,最大值为n+n﹣1=2n﹣1,这2个整数之和共有2n﹣1﹣3+1=2n﹣3种不同情况;
答案为:(2n﹣3);
探究二:
(1)从1,2,3,4这4个整数中任取3个整数,这3个整数之和的最小值为1+2+3=6,最大值为2+3+4=9,这3个整数之和共有9﹣6+1=4种不同情况;
故答案为:4;
(2)从1,2,3,…,n(n为整数,且n≥4)这n个整数中任取3个整数,这3个整数之和的最小值为1+2+3=6,最大值为n+(n﹣1)+(n﹣2)=3n﹣3,这3个整数之和共有3n﹣3﹣6+1=3n﹣8种不同结果,
故答案为:(3n﹣8);
探究三:
从1,2,3,…,n(n为整数,且n≥5)这n个整数中任取4个整数,这4个整数之和的最小值为1+2+3+4=10,最大值为n+(n﹣1)+(n﹣2)+(n﹣3)=4n﹣6,因此这4个整数之和共有4n﹣6﹣10+1=4n﹣15种不同结果,
归纳总结:
从1,2,3,…,n(n为整数,且n≥5)这n个整数中任取a个整数,这a个整数之和的最小值为1+2+…+a=,最大值为n+(n﹣1)+(n﹣2)+(n﹣3)+…+(n﹣a+1)=na﹣,因此这a个整数之和共有na﹣﹣+1=a(n﹣a)+1种不同结果,
答案为:[a(n﹣a)+1];
问题解决:
将n=100,a=5,代入a(n﹣a)+1得;5×(100﹣5)+1=476,
答案为:476;
拓展延伸:
(1)设从1,2,3,…,36这36个整数中任取a个整数,使得取出的这些整数之和共有204种不同的结果,由上述结论得,
a(36﹣a)+1=204,解得,a=7或a=29;
答:从1,2,3,…,36这36个整数中任取7个整数或取29个整数,能使取出的这些整数之和共有204种不同的结果;
(2)根据上述规律,从(n+1)个连续整数中任取a个整数,这a个整数之和共有[a(n+1﹣a)+1]种不同的结果,
答案为:[a(n+1﹣a)+1].
概率的进一步认识
单元测试
一.选择题
1.不透明布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出一个球,两次都摸出白球的概率是( )
A.
B.
C.
D.
2.如图是两个可以自由转动的转盘,其中一个转盘平均分为4份,另一个转盘平均分为3份,两个转盘分别标有数字;同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为5的概率是( )
A.
B.
C.
D.
3.从分别写有数字1,2,3,4,5的5张卡片中任意取出两张,把第一张卡片上的数字作为十位数字,第二张卡片上的数字作为个位数字,组成一个两位数,则所组成的数是5的倍数的概率是( )
A.
B.
C.
D.
4.在一个口袋中有5个完全相同的小球,把它们分别标号为1,2,3,4,5,随机摸出一个小球不放回,再随机摸出一个小球,则两次摸出小球的标号之和能被3整除的概率是( )
A.
B.
C.
D.
5.如图,小球从A口往下落,在每个交又口都有向左或向右两种可能,且可能性相同,则小球最终从E口落出的概率为( )
A.
B.
C.
D.
6.某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线统计图,那么符合这一结果的实验最有可能的是( )
A.掷一枚质地均匀的硬币,落地时结果是“正面向上”
B.掷一个质地均匀的正六面体骰子,落地时朝上的面点数是6
C.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D.袋子中有1个红球和2个黄球,只有颜色上的区别,从中随机取出一个球是黄球
7.在“众志成城,共战疫情”党员志愿者进社区服务活动中,小晴和小霞分别从“A,B,C三个社区”中随机选择一个参加活动,两人恰好选择同一社区的概率是( )
A.
B.
C.
D.
8.如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5m,宽为4m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了②所示的折线统计图,由此他估计不规则图案的面积大约为( )
A.6m2
B.7m2
C.8m2
D.9m2
9.从长度分别为1cm、3cm、5cm、6cm四条线段中随机取出三条,则能够组成三角形的概率为( )
A.
B.
C.
D.
10.下列事件的概率,与“任意选2个人,恰好同月过生日”这一事件的概率相等的是( )
A.任意选2个人,恰好生肖相同
B.任意选2个人,恰好同一天过生日
C.任意掷2枚骰子,恰好朝上的点数相同
D.任意掷2枚硬币,恰好朝上的一面相同
二.填空题
11.不透明的袋子中装有红、蓝小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到相同颜色的小球的概率是
.
12.技术变革带来产品质量的提升.某企业技术变革后,抽检某一产品2020件,欣喜发现产品合格的频率已达到0.9911,依此我们可以估计该产品合格的概率为
.(结果要求保留两位小数)
13.某校开展以“我和我的祖国”为主题的“大合唱”活动,七年级准备从小明、小东、小聪三名男生和小红、小慧两名女生中各随机选出一名男生和一名女生担任领唱,则小聪和小慧被同时选中的概率是
.
14.在“抛掷正六面体”的试验中,正六面体的六个面分别标有数字“1”“2”“3”“4”“5”“6”,在试验次数很大时,数字“6”朝上的频率的变化趋势接近的值是
.
15.要考察某运动员罚篮命中率,下表是在多次测试中的统计数据:
罚进个数
80
140
293
523
613
823
罚球总数
110
182
396
701
820
1098
估计该运动员罚篮命中的概率是
.(结果精确到0.01)
16.在一个不透明的袋子中装有3个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.7附近,则袋子中红球约有
个.
17.现有5张正面分别标有数字﹣3,﹣1,1,2,4的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为m,n.则一次函数y=mx+n经过第一、二、四象限的概率是
.
18.2019年12月,湖北省武汉市出现多起病毒性肺炎病例,2020年1月20日,习近平总书记对新型冠状病毒感染的肺炎疫情作出重要指示,强调要把人民群众生命安全和身体健康放在第一位,坚决遏制疫情蔓延势头.全国各地的医护人员积极报名参与抗疫第一线的支援工作.重庆市某医院准备从报名的甲、乙、丙、丁四名医生中随机选择2人去支援湖北,那么乙、丙两人中至少有一人被选中的概率为
.
三.解答题
19.从2021年起,江苏省高考采用“3+1+2”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选1科,“2”是指在化学、生物、思想政治、地理4科中任选2科.
(1)若小丽在“1”中选择了历史,在“2”中已选择了地理,则她选择生物的概率是
;
(2)若小明在“1”中选择了物理,用画树状图的方法求他在“2”中选化学、生物的概率.
20.在1、2、3、4这四个数中,先任意取一个数a,然后在余下的数中任意取出一个数b,组成一个点(a,b).求组成的点(a,b)恰好横坐标为偶数且纵坐标为奇数的概率(请用“画树状图”或“列表”等方法写出分析过程).
21.某校开展征文活动,征文主题只能从“爱国”、“敬业”、“诚信”、“友善”四个主题中选择一个,每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.
(1)将上面的条形统计图补充完整;
(2)在扇形统计图中,选择“爱国”主题所对应的圆心角是
°.
(3)如果该校七年级共有1200名考生,请估计选择以“友善”为主题的七年级学生有
名:
(4)学生会宣传部有七年级的2名男生和2名女生,现从中随机挑选2名同学参加“主题征文”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
22.为落实我市关于开展中小学课后服务工作的要求,某学校开设了四门校本课程供学生选择:A.趣味数学;B.博乐阅读;C.快乐英语;D.硬笔书法.某年级共有100名学生选择了A课程,为了解本年级选择A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试,将他们的成绩(百分制)分成六组,绘制成频数分布直方图.
(1)已知70≤x<80这组的数据为:72,73,74,75,76,76,79.则这组数据的中位数是
;众数是
;
(2)根据题中信息,估计该年级选择A课程学生成绩在80≤x<90的总人数;
(3)该年级学生小乔随机选取了一门课程,则小乔选中课程D的概率是
;
(4)该年级每名学生选两门不同的课程,小张和小王在选课程的过程中,若第一次都选了课程C,那么他俩第二次同时选择课程A或课程B的概率是多少?请用列表法或树状图的方法加以说明.
23.实际问题:
某商场为鼓励消费,设计了抽奖活动,方案如下:根据不同的消费金额,每次抽奖时可以从100张面值分别为1元、2元、3元、…、100元的奖券中(面值为整数),一次任意抽取2张、3张、4张、…等若干张奖券,奖券的面值金额之和即为优惠金额.某顾客获得了一次抽取5张奖券的机会,小明想知道该顾客共有多少种不同的优惠金额?
问题建模:
从1,2,3,…,n(n为整数,且n≥3)这n个整数中任取a
(1<a<n)个整数,这a个整数之和共有多少种不同的结果?
模型探究:
我们采取一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,从中找出解决问题的方法.
探究一:
(1)从1,2,3这3个整数中任取2个整数,这2个整数之和共有多少种不同的结果?
表①
所取的2个整数
1,2
1,3
2,3
2个整数之和
3
4
5
如表①,所取的2个整数之和可以为3,4,5,也就是从3到5的连续整数,其中最小是3,最大是5,所以共有3种不同的结果.
(2)从1,2,3,4这4个整数中任取2个整数,这2个整数之和共有多少种不同的结果?
表②
所取的2个整数
1,2
1,3
1,4
2,3
2,4
3,4
2个整数之和
3
4
5
5
6
7
如表②,所取的2个整数之和可以为3,4,5,6,7,也就是从3到7的连续整数,其中最小是3,最大是7,所以共有5种不同的结果.
(3)从1,2,3,4,5这5个整数中任取2个整数,这2个整数之和共有
种不同的结果.
(4)从1,2,3,…,n(n为整数,且n≥3)这n个整数中任取2个整数,这2个整数之和共有
种不同的结果.
探究二:
(1)从1,2,3,4这4个整数中任取3个整数,这3个整数之和共有
种不同的结果.
(2)从1,2,3,…,n(n为整数,且n≥4)这n个整数中任取3个整数,这3个整数之和共有
种不同的结果.
探究三:
从1,2,3,…,n(n为整数,且n≥5)这n个整数中任取4个整数,这4个整数之和共有
种不同的结果.
归纳结论:
从1,2,3,…,n(n为整数,且n≥3)这n个整数中任取a(1<a<n)个整数,这a个整数之和共有
种不同的结果.
问题解决:
从100张面值分别为1元、2元、3元、…、100元的奖券中(面值为整数),一次任意抽取5张奖券,共有
种不同的优惠金额.
拓展延伸:
(1)从1,2,3,…,36这36个整数中任取多少个整数,使得取出的这些整数之和共有204种不同的结果?(写出解答过程)
(2)从3,4,5,…,n+3(n为整数,且n≥2)这(n+1)个整数中任取a(1<a<n+1)个整数,这a个整数之和共有
种不同的结果.
参考答案
1.A.
2.C.
3.C
4.B
5.B
6.B
7.A
8.B
9.A
10.A
11..
12.0.99
13.
14.
15.0.75
16.7
17.:
18.
19.解:(1)在“2”中已选择了地理,从剩下的化学、生物,思想品德三科中选一科,因此选择生物的概率为;
答案为:;
(2)用树状图表示所有可能出现的结果如下:
共有12种可能出现的结果,其中选中“化学”“生物”的有2种,
∴P(化学生物)==.
20.解:画树状图为:
共有12种等可能的结果数,其中组成的点(a,b)恰好横坐标为偶数且纵坐标为奇数的结果数为4,
所以组成的点(a,b)恰好横坐标为偶数且纵坐标为奇数的概率==.
21.解:(1)调查的总人数为3÷6%=50(人),
所以以“友善”为主题的人数为50×30%=15(人),
条形统计图补充为:
(2)在扇形统计图中,选择“爱国”主题所对应的圆心角的度数为360°×=144°;
(3)1200×30%=360,
所以估计选择以“友善”为主题的七年级学生有360名;
答案为144,360;
(4)画树状图为:
共有12种等可能的结果数,其中“1男1女”的结果数为8,
所以恰好选中“1男1女”的概率==.
22.解:(1)在72,73,74,75,76,76,79这组已经按从小到大排列好的数据中,中位数为75,众数为76;
故答案为:75,76;
(2)观察直方图,抽取的30名学生成绩在80≤x<90范围内选取A课程的有9人,所占比为,
那么估计该年级100名学生,学生成绩在80≤x<90范围内,选取A课程的总人数为(人);
(3)因为学校开设了四门校本课程供学生选择,小乔随机选取一门课程,则他选中课程D的概率为;
故答案为:;
(4)因该年级每名学生选两门不同的课程,第一次都选了课程C,列树状图如下:
等可能结果共有9种,他俩第二次同时选择课程A或课程B的有2种,
所以,他俩第二次同时选择课程A或课程B的概率是.
23.解:探究一:
(3)从1,2,3,4,5这5个整数中任取2个整数,这2个整数之和最小值为1+2=3,最大值为4+5=9,这2个整数之和共有9﹣3+1=7种不同情况;
故答案为:7;
(4)从1,2,3,…,n(n为整数,且n≥3)这n个整数中任取2个整数,这2个整数之和最小值为1+2=3,最大值为n+n﹣1=2n﹣1,这2个整数之和共有2n﹣1﹣3+1=2n﹣3种不同情况;
答案为:(2n﹣3);
探究二:
(1)从1,2,3,4这4个整数中任取3个整数,这3个整数之和的最小值为1+2+3=6,最大值为2+3+4=9,这3个整数之和共有9﹣6+1=4种不同情况;
故答案为:4;
(2)从1,2,3,…,n(n为整数,且n≥4)这n个整数中任取3个整数,这3个整数之和的最小值为1+2+3=6,最大值为n+(n﹣1)+(n﹣2)=3n﹣3,这3个整数之和共有3n﹣3﹣6+1=3n﹣8种不同结果,
故答案为:(3n﹣8);
探究三:
从1,2,3,…,n(n为整数,且n≥5)这n个整数中任取4个整数,这4个整数之和的最小值为1+2+3+4=10,最大值为n+(n﹣1)+(n﹣2)+(n﹣3)=4n﹣6,因此这4个整数之和共有4n﹣6﹣10+1=4n﹣15种不同结果,
归纳总结:
从1,2,3,…,n(n为整数,且n≥5)这n个整数中任取a个整数,这a个整数之和的最小值为1+2+…+a=,最大值为n+(n﹣1)+(n﹣2)+(n﹣3)+…+(n﹣a+1)=na﹣,因此这a个整数之和共有na﹣﹣+1=a(n﹣a)+1种不同结果,
答案为:[a(n﹣a)+1];
问题解决:
将n=100,a=5,代入a(n﹣a)+1得;5×(100﹣5)+1=476,
答案为:476;
拓展延伸:
(1)设从1,2,3,…,36这36个整数中任取a个整数,使得取出的这些整数之和共有204种不同的结果,由上述结论得,
a(36﹣a)+1=204,解得,a=7或a=29;
答:从1,2,3,…,36这36个整数中任取7个整数或取29个整数,能使取出的这些整数之和共有204种不同的结果;
(2)根据上述规律,从(n+1)个连续整数中任取a个整数,这a个整数之和共有[a(n+1﹣a)+1]种不同的结果,
答案为:[a(n+1﹣a)+1].
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
