华东师大版八年级上册14.2勾股定理的应用课件(共22张ppt)
文档属性
| 名称 | 华东师大版八年级上册14.2勾股定理的应用课件(共22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
2.勾股定理的应用
华东师大版八年级上学期
第14章
《勾股定理》
学而不疑则怠,疑而不探则空
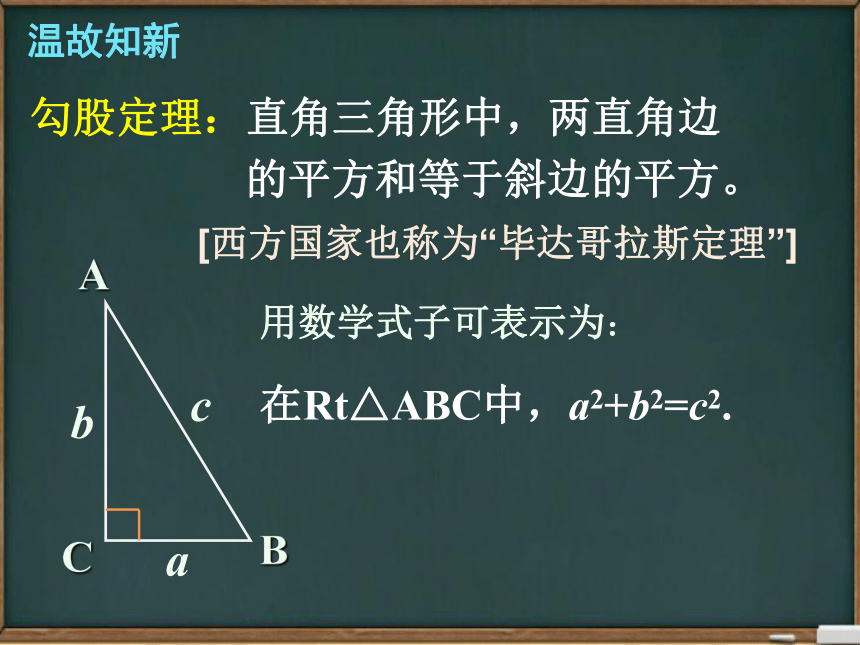
勾股定理:直角三角形中,两直角边
的平方和等于斜边的平方。
[西方国家也称为“毕达哥拉斯定理”]
用数学式子可表示为:
C
B
a
b
A
c
温故知新
在Rt△ABC中,a2+b2=c2.
一、直接运用勾股定理求三角形的
边长、周长、高、面积;
B
A
C
应用探索
例:如图,在Rt△ABC中,∠C=90?,
AB=25cm,AC=20cm.
则BC=
,
AB边的高=
,
l△ABC=
,
S△ABC=
.
15cm
12cm
60cm
150cm2
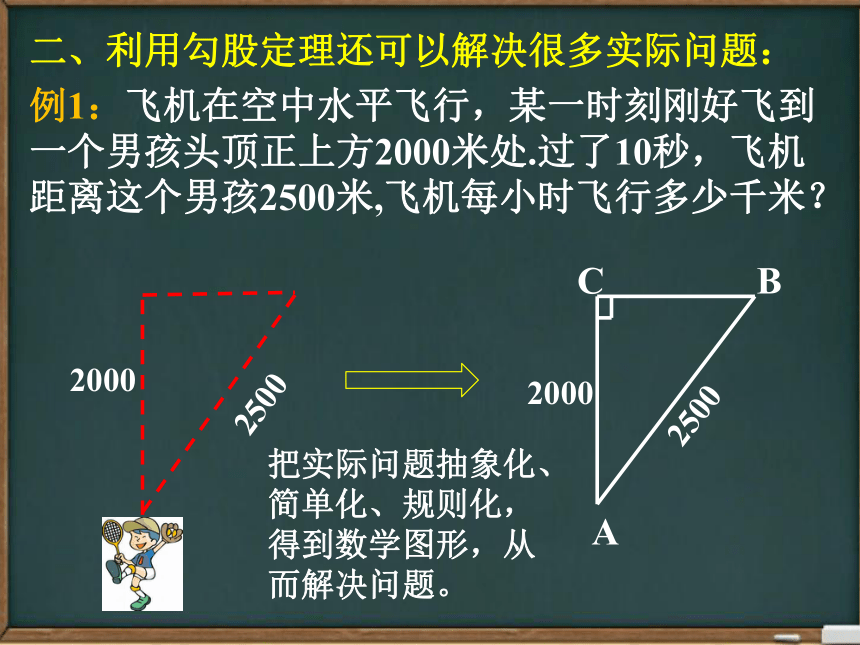
二、利用勾股定理还可以解决很多实际问题:
2500
2000
C
B
A
2000
例1:飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方2000米处.过了10秒,飞机距离这个男孩2500米,飞机每小时飞行多少千米?
2500
把实际问题抽象化、简单化、规则化,得到数学图形,从而解决问题。
2500
2000
C
B
A
例1:飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方2000米处.过了10秒,飞机距离这个男孩2500米,飞机每小时飞行多少千米?
解:由题意,得
在Rt△ABC中,∠C=90?,
AB=2500m,AC=2000m.
根据勾股定理,得
BC=
AB2-AC2=1500m
则1500÷10×3600=540km/h
答:飞机每小时飞行540千米.
例2:某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,为了安全起见梯子的底部与墙基的距离是2.5米。请问消防队员能否进入三楼灭火?
A
B
C
解:依题意,如图,AB为建筑物,
AC是云梯的长,则BC=2.5m,
根据勾股定理,在Rt△ABC中,
BC2+AB2=AC2,
所以AB
2=6.52-2.52=36=62.
因此消防队员能进入三楼灭火。
A
B
C
D
1m
2m
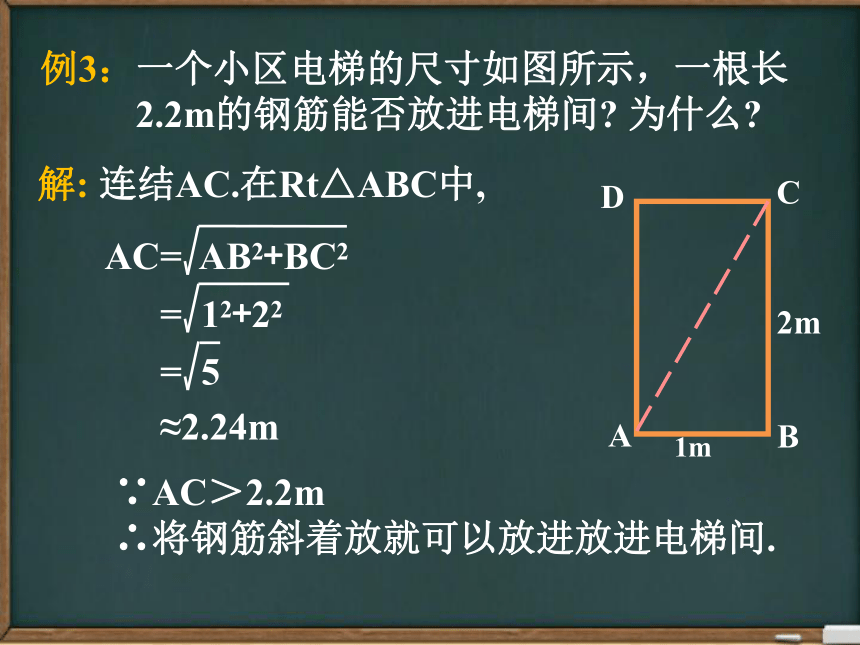
例3:一个小区电梯的尺寸如图所示,一根长
2.2m的钢筋能否放进电梯间?
为什么?
解:
连结AC.在Rt△ABC中,
∵AC>2.2m
∴将钢筋斜着放就可以放进放进电梯间.
AC=
AB2+BC2
=
12+22
=
5
≈2.24m
例4:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?
在Rt△OCD中,由勾股定理得
CH=0.6+2.3=2.9(米)>2.5(米)
因此高度上有0.4米的余量,
所以卡车能通过厂门.
解:如图点D在离厂门中线0.8米处,且CD⊥AB,
则OC=1米,OD=0.8米.
CD=
OC2-OD2
=
12-0.82
=0.6m
A
C
B
D
O
H
2米
2.3米
例5:某农民开垦出一块三边长分别为7m、8m、9m三角形地块准备种植花生,聪明的同学,你能帮他算一算这块地的面积吗?
不是直角三角形,怎么办呢?
7
8
9
72+82≠92
7
8
9
A
B
C
解:如图,过点A作AD⊥BC于D
得Rt△ADB和Rt△ADC.
D
由勾股定理得
AD=
AB2-BD2
=
AC2-CD2
即82-BD2=
72-(9-BD)2
解得BD=
163
则AD=
82-(
)2
163
=
5
8
3
∴这块地的面积为
5
8
3
9
2
×
=12
5
m2.
例6:你能画出下列长度的线段吗?
2
3
5
6
10
17
1
1
2
1
2
3
1
2
5
2
3
5
1
5
6
1
3
10
例7:如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.(精确到0.01cm)
A
B
C
D
A
D
A'
B
C
B'
例8:如图,现要在此楼梯旁建造无障碍通道,经测量每格楼梯的高为11.25cm,宽20cm,你能求出通道的长度吗?
在Rt△ABC中,∠ACB=90°
∴AB2=AC2+BC2(勾股定理)
解:由题意得AC=11.25×4=45cm,
BC=20×3=60cm.
∴通道的长度为75cm.
∴AB=
AC2+BC2
=
452+602
=75cm
A
B
C
例9:如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD.
A
B
C
D
提示:等式的证明,要根据条件选择从左到右或从右到左的过程进行变形。此题等式左边出现了线段的平方,应构造直角三角形。
A
B
C
D
证明:
过A作AE⊥BC于E
E
∵AB=AC,
∴BE=CE
在Rt△ADE中,
AD2=AE2+DE2
在Rt△ABE中,
AB2=AE2+BE2
∴
AD2-AB2=(AE2+DE2)-(AE2+BE2)
=
DE2-BE2
=
(DE+BE)·(
DE-BE)
=
(DE+CE)·(
DE-BE)
=BD·CD
1、如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了___步路,
却踩伤了花草。
(假设1米为2步)
5
4
小试身手
3
4
A
B
C
“路”
2、如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?
18
30
24
1、已知直角三角形一条直角边长为8,另两边长为连续奇数,求这个三角形的周长。
2、如图,在△ABC中,
AB=13,AD=12,AC=15,
CD=9.
求△ABC的面积.
3、在等腰△ABC中,AB=AC=13cm,BC=10cm,求△ABC的面积及AC边上的高。
课后作业
A
B
D
C
5、已知直角三角形的周长为12,斜边长为5,求这个三角形的面积。
6、四边形ABCD中,AB=BC=2,
CD=3,DA=1,且∠B=90o,
求∠DAB的度数。
4、等边三角形ABC的边长是6.求△ABC的面积.
7、如图所示,现在已测得长方体木块的长2,宽1,高3.一只蜘蛛潜伏在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处。蜘蛛急于想捉住苍蝇,沿着长方体的表面向上爬,它要从点A爬到点B处,有无数条路线,它们有长有短,蜘蛛究竟应该沿着怎样的路线爬上去,所走的路程会最短。你能帮蜘蛛找到最短路径吗?
A
B
8、在一棵树的20米的B处有两只猴子,其中一只猴子爬下树走到离树40米的A处,另一只爬到树顶D后直接跳向A处,且测得AD为50米,求BD的长.
D
C
A
B
9、已知矩形纸片ABCD中,AD=4cm,
AB=10cm,按如图方式折叠,折痕是
EF,求DE的长度.
(B)
A
B
C
D
E
F
(C)
2.勾股定理的应用
华东师大版八年级上学期
第14章
《勾股定理》
学而不疑则怠,疑而不探则空
勾股定理:直角三角形中,两直角边
的平方和等于斜边的平方。
[西方国家也称为“毕达哥拉斯定理”]
用数学式子可表示为:
C
B
a
b
A
c
温故知新
在Rt△ABC中,a2+b2=c2.
一、直接运用勾股定理求三角形的
边长、周长、高、面积;
B
A
C
应用探索
例:如图,在Rt△ABC中,∠C=90?,
AB=25cm,AC=20cm.
则BC=
,
AB边的高=
,
l△ABC=
,
S△ABC=
.
15cm
12cm
60cm
150cm2
二、利用勾股定理还可以解决很多实际问题:
2500
2000
C
B
A
2000
例1:飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方2000米处.过了10秒,飞机距离这个男孩2500米,飞机每小时飞行多少千米?
2500
把实际问题抽象化、简单化、规则化,得到数学图形,从而解决问题。
2500
2000
C
B
A
例1:飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方2000米处.过了10秒,飞机距离这个男孩2500米,飞机每小时飞行多少千米?
解:由题意,得
在Rt△ABC中,∠C=90?,
AB=2500m,AC=2000m.
根据勾股定理,得
BC=
AB2-AC2=1500m
则1500÷10×3600=540km/h
答:飞机每小时飞行540千米.
例2:某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,为了安全起见梯子的底部与墙基的距离是2.5米。请问消防队员能否进入三楼灭火?
A
B
C
解:依题意,如图,AB为建筑物,
AC是云梯的长,则BC=2.5m,
根据勾股定理,在Rt△ABC中,
BC2+AB2=AC2,
所以AB
2=6.52-2.52=36=62.
因此消防队员能进入三楼灭火。
A
B
C
D
1m
2m
例3:一个小区电梯的尺寸如图所示,一根长
2.2m的钢筋能否放进电梯间?
为什么?
解:
连结AC.在Rt△ABC中,
∵AC>2.2m
∴将钢筋斜着放就可以放进放进电梯间.
AC=
AB2+BC2
=
12+22
=
5
≈2.24m
例4:一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?
在Rt△OCD中,由勾股定理得
CH=0.6+2.3=2.9(米)>2.5(米)
因此高度上有0.4米的余量,
所以卡车能通过厂门.
解:如图点D在离厂门中线0.8米处,且CD⊥AB,
则OC=1米,OD=0.8米.
CD=
OC2-OD2
=
12-0.82
=0.6m
A
C
B
D
O
H
2米
2.3米
例5:某农民开垦出一块三边长分别为7m、8m、9m三角形地块准备种植花生,聪明的同学,你能帮他算一算这块地的面积吗?
不是直角三角形,怎么办呢?
7
8
9
72+82≠92
7
8
9
A
B
C
解:如图,过点A作AD⊥BC于D
得Rt△ADB和Rt△ADC.
D
由勾股定理得
AD=
AB2-BD2
=
AC2-CD2
即82-BD2=
72-(9-BD)2
解得BD=
163
则AD=
82-(
)2
163
=
5
8
3
∴这块地的面积为
5
8
3
9
2
×
=12
5
m2.
例6:你能画出下列长度的线段吗?
2
3
5
6
10
17
1
1
2
1
2
3
1
2
5
2
3
5
1
5
6
1
3
10
例7:如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.(精确到0.01cm)
A
B
C
D
A
D
A'
B
C
B'
例8:如图,现要在此楼梯旁建造无障碍通道,经测量每格楼梯的高为11.25cm,宽20cm,你能求出通道的长度吗?
在Rt△ABC中,∠ACB=90°
∴AB2=AC2+BC2(勾股定理)
解:由题意得AC=11.25×4=45cm,
BC=20×3=60cm.
∴通道的长度为75cm.
∴AB=
AC2+BC2
=
452+602
=75cm
A
B
C
例9:如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD.
A
B
C
D
提示:等式的证明,要根据条件选择从左到右或从右到左的过程进行变形。此题等式左边出现了线段的平方,应构造直角三角形。
A
B
C
D
证明:
过A作AE⊥BC于E
E
∵AB=AC,
∴BE=CE
在Rt△ADE中,
AD2=AE2+DE2
在Rt△ABE中,
AB2=AE2+BE2
∴
AD2-AB2=(AE2+DE2)-(AE2+BE2)
=
DE2-BE2
=
(DE+BE)·(
DE-BE)
=
(DE+CE)·(
DE-BE)
=BD·CD
1、如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了___步路,
却踩伤了花草。
(假设1米为2步)
5
4
小试身手
3
4
A
B
C
“路”
2、如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?
18
30
24
1、已知直角三角形一条直角边长为8,另两边长为连续奇数,求这个三角形的周长。
2、如图,在△ABC中,
AB=13,AD=12,AC=15,
CD=9.
求△ABC的面积.
3、在等腰△ABC中,AB=AC=13cm,BC=10cm,求△ABC的面积及AC边上的高。
课后作业
A
B
D
C
5、已知直角三角形的周长为12,斜边长为5,求这个三角形的面积。
6、四边形ABCD中,AB=BC=2,
CD=3,DA=1,且∠B=90o,
求∠DAB的度数。
4、等边三角形ABC的边长是6.求△ABC的面积.
7、如图所示,现在已测得长方体木块的长2,宽1,高3.一只蜘蛛潜伏在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处。蜘蛛急于想捉住苍蝇,沿着长方体的表面向上爬,它要从点A爬到点B处,有无数条路线,它们有长有短,蜘蛛究竟应该沿着怎样的路线爬上去,所走的路程会最短。你能帮蜘蛛找到最短路径吗?
A
B
8、在一棵树的20米的B处有两只猴子,其中一只猴子爬下树走到离树40米的A处,另一只爬到树顶D后直接跳向A处,且测得AD为50米,求BD的长.
D
C
A
B
9、已知矩形纸片ABCD中,AD=4cm,
AB=10cm,按如图方式折叠,折痕是
EF,求DE的长度.
(B)
A
B
C
D
E
F
(C)
