_教科 课标版_必修1_ 第一章 运动的描述 _ 6. 匀变速直线运动位移与时间的关系 _课件24张PPT
文档属性
| 名称 | _教科 课标版_必修1_ 第一章 运动的描述 _ 6. 匀变速直线运动位移与时间的关系 _课件24张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-28 08:17:48 | ||
图片预览





文档简介
【割圆术】—刘徽
圆内正多边形的边数越多,其周长和面积就越接近圆的周长和面积.
割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣
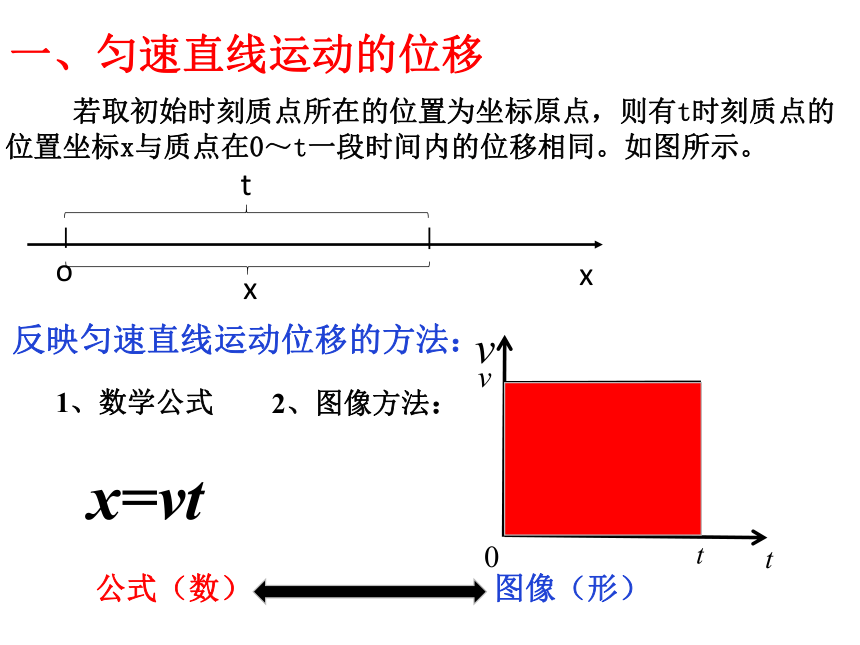
一、匀速直线运动的位移
1、数学公式
x=vt
2、图像方法:
若取初始时刻质点所在的位置为坐标原点,则有t时刻质点的位置坐标x与质点在0~t一段时间内的位移相同。如图所示。
o
x
t
x
反映匀速直线运动位移的方法:
公式(数)
图像(形)
二、匀变速直线运动位移与时间关系的探究
猜想:对于匀变速直线运动,位移与其v-t图像,是不是也有类似的关系?
(一)实验探究
设计实验方案,并回答下列问题
①实验中我们要验证的是哪两个量的关系?
②如何获得我们实验所要研究的匀变速直线运动,怎么验证我们所获得的运动是匀变速直线运动
③实验中我们需要哪些实验器材,如何测量小车运动速度
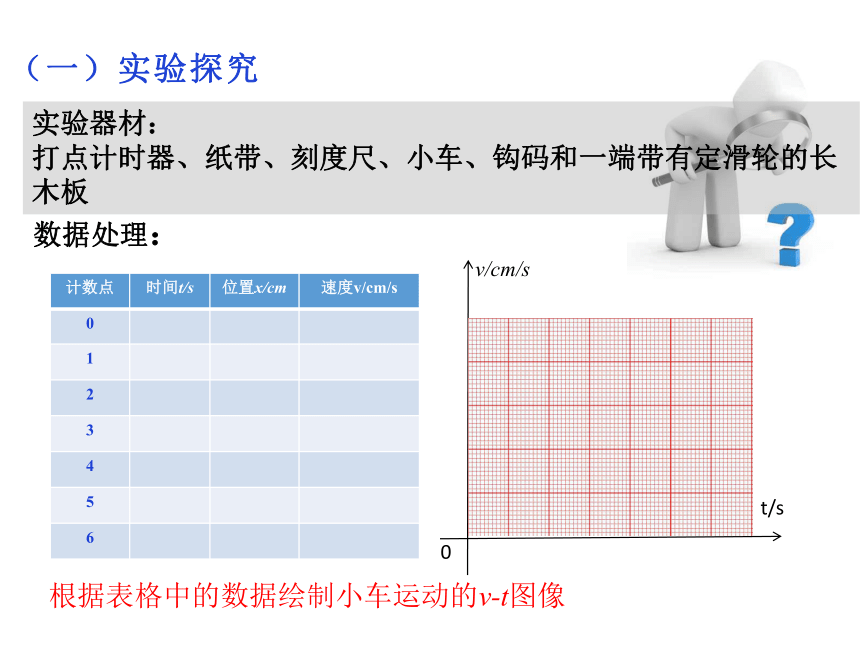
(一)实验探究
实验器材:
打点计时器、纸带、刻度尺、小车、钩码和一端带有定滑轮的长木板
数据处理:
计数点
时间t/s
位置x/cm
速度v/cm/s
0
1
2
3
4
5
6
根据表格中的数据绘制小车运动的v-t图像
0
v/cm/s
t/s
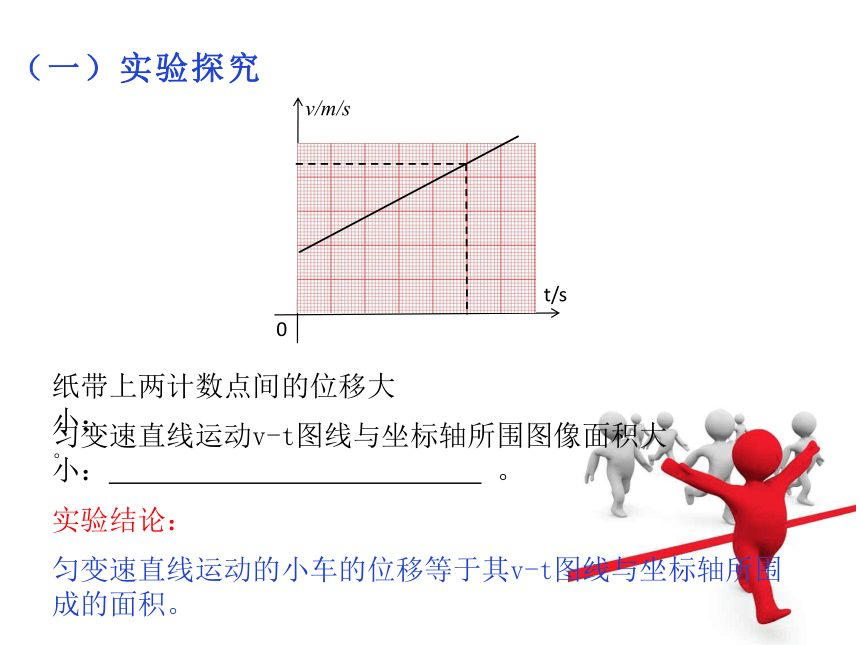
(一)实验探究
纸带上两计数点间的位移大小: 。
匀变速直线运动v-t图线与坐标轴所围图像面积大小: 。
实验结论:
匀变速直线运动的小车的位移等于其v-t图线与坐标轴所围成的面积。
0
v/m/s
t/s
思考与讨论1:
下面的方法可以估算计数点0到计数点5的位移吗?为什么?
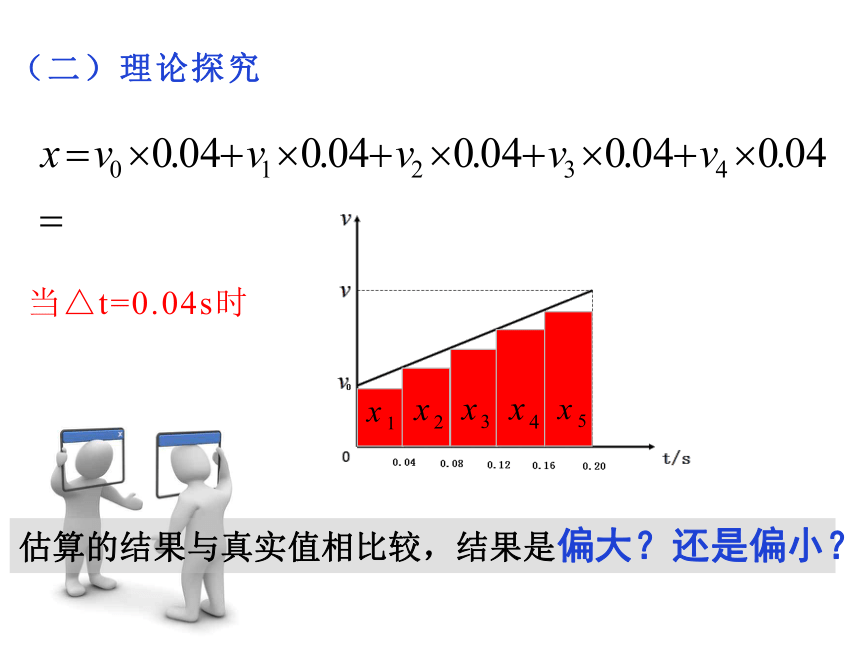
(二)理论探究
当△t=0.04s时
(二)理论探究
估算的结果与真实值相比较,结果是偏大?还是偏小?
思考与讨论2:
将每一个打出来的点都标为计数点,用相同的方法计算如下:
计算结果与第一次计算结果相比较,误差会怎样?
(二)理论探究
当△t=0.02s时
(二)理论探究
思考与讨论3:
如果相邻两个计数点之间的时间就更小(为0.01s),同样用这种方法计算如下:
计算结果与第二次计算结果相比较,误差会怎样?
(二)理论探究
当△t=0.01s时
(二)理论探究
在匀变速直线运动的v-t图像中,图线与时间轴围成的面积也代表位移。
(三)匀变速直线运动位移时间关系式推导
②两种特殊情况
当v0=0时,公式为
当a=0时,公式为 x=vot
(四)匀变速直线运动位移时间关系式理解
①矢量性
思考:公式中哪些物理量是矢量?
位移、初速度、加速度
应用公式时首先要选择正方向,一般我们选择初速度的方向为正方向。
③公式与图像的对应关系
(四)匀变速直线运动位移时间关系式理解
④位移与时间的图像
思考:对于匀速直线运动,x=vt,位移与时间成正比,我们可以用图像表示为
x
t
0
(四)匀变速直线运动位移时间关系式理解
④位移与时间的图像
思考:对于匀变速直线运动它的位移图像是什么样子的呢?其位移时间关系式为x=v0t+ at2,它与我们初中学习的一次函数还是二次函数相像呢?
思考:匀变速直线运动的x-t图线是一条抛物线,这与物体做直线运动相矛盾吗?
(四)匀变速直线运动位移时间关系式理解
通过今天的学习,你的收获是什么?
课堂小结:
课本40页第1题和第2题
课后作业:
勤思善学促进步,熟能生巧是关键!
三、课堂习题
一辆汽车以20m/s的速度行驶,现因故刹车,刹车过程中做匀减速直线运动,并最终停止运动,已知汽车刹车过程的加速度大小是5m/s2。则汽车从开始刹车经过5s所通过的距离是多少?
(一)用Excel绘制v-t图线
(二)用Excel绘制x-t图线
圆内正多边形的边数越多,其周长和面积就越接近圆的周长和面积.
割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣
一、匀速直线运动的位移
1、数学公式
x=vt
2、图像方法:
若取初始时刻质点所在的位置为坐标原点,则有t时刻质点的位置坐标x与质点在0~t一段时间内的位移相同。如图所示。
o
x
t
x
反映匀速直线运动位移的方法:
公式(数)
图像(形)
二、匀变速直线运动位移与时间关系的探究
猜想:对于匀变速直线运动,位移与其v-t图像,是不是也有类似的关系?
(一)实验探究
设计实验方案,并回答下列问题
①实验中我们要验证的是哪两个量的关系?
②如何获得我们实验所要研究的匀变速直线运动,怎么验证我们所获得的运动是匀变速直线运动
③实验中我们需要哪些实验器材,如何测量小车运动速度
(一)实验探究
实验器材:
打点计时器、纸带、刻度尺、小车、钩码和一端带有定滑轮的长木板
数据处理:
计数点
时间t/s
位置x/cm
速度v/cm/s
0
1
2
3
4
5
6
根据表格中的数据绘制小车运动的v-t图像
0
v/cm/s
t/s
(一)实验探究
纸带上两计数点间的位移大小: 。
匀变速直线运动v-t图线与坐标轴所围图像面积大小: 。
实验结论:
匀变速直线运动的小车的位移等于其v-t图线与坐标轴所围成的面积。
0
v/m/s
t/s
思考与讨论1:
下面的方法可以估算计数点0到计数点5的位移吗?为什么?
(二)理论探究
当△t=0.04s时
(二)理论探究
估算的结果与真实值相比较,结果是偏大?还是偏小?
思考与讨论2:
将每一个打出来的点都标为计数点,用相同的方法计算如下:
计算结果与第一次计算结果相比较,误差会怎样?
(二)理论探究
当△t=0.02s时
(二)理论探究
思考与讨论3:
如果相邻两个计数点之间的时间就更小(为0.01s),同样用这种方法计算如下:
计算结果与第二次计算结果相比较,误差会怎样?
(二)理论探究
当△t=0.01s时
(二)理论探究
在匀变速直线运动的v-t图像中,图线与时间轴围成的面积也代表位移。
(三)匀变速直线运动位移时间关系式推导
②两种特殊情况
当v0=0时,公式为
当a=0时,公式为 x=vot
(四)匀变速直线运动位移时间关系式理解
①矢量性
思考:公式中哪些物理量是矢量?
位移、初速度、加速度
应用公式时首先要选择正方向,一般我们选择初速度的方向为正方向。
③公式与图像的对应关系
(四)匀变速直线运动位移时间关系式理解
④位移与时间的图像
思考:对于匀速直线运动,x=vt,位移与时间成正比,我们可以用图像表示为
x
t
0
(四)匀变速直线运动位移时间关系式理解
④位移与时间的图像
思考:对于匀变速直线运动它的位移图像是什么样子的呢?其位移时间关系式为x=v0t+ at2,它与我们初中学习的一次函数还是二次函数相像呢?
思考:匀变速直线运动的x-t图线是一条抛物线,这与物体做直线运动相矛盾吗?
(四)匀变速直线运动位移时间关系式理解
通过今天的学习,你的收获是什么?
课堂小结:
课本40页第1题和第2题
课后作业:
勤思善学促进步,熟能生巧是关键!
三、课堂习题
一辆汽车以20m/s的速度行驶,现因故刹车,刹车过程中做匀减速直线运动,并最终停止运动,已知汽车刹车过程的加速度大小是5m/s2。则汽车从开始刹车经过5s所通过的距离是多少?
(一)用Excel绘制v-t图线
(二)用Excel绘制x-t图线
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
