教科2003课标版 必修1 第一章 运动的描述 6. 匀变速直线运动位移与时间的关系 _课件25张PPT
文档属性
| 名称 | 教科2003课标版 必修1 第一章 运动的描述 6. 匀变速直线运动位移与时间的关系 _课件25张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 825.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-28 10:15:46 | ||
图片预览





文档简介
伽利略相信,自然界是简单的,自然规律也是简单的。我们研究问题,总是从最简单的开始,通过对简单问题的研究,认识了许多复杂的规律,这是科学探究常用的一种方法。
思想
一、匀速直线运动的位移
匀速直线运动的位移
v
x =
vt
5
10
0
t/s
10
5
v/m·s-1
结论:
对于匀速直线运动,物体的位移对应着v – t 图象中一块矩形的面积。
x = vt
v/m·s-1
t/s
2
6
4
10
8
3
4
5
6
0
2
1
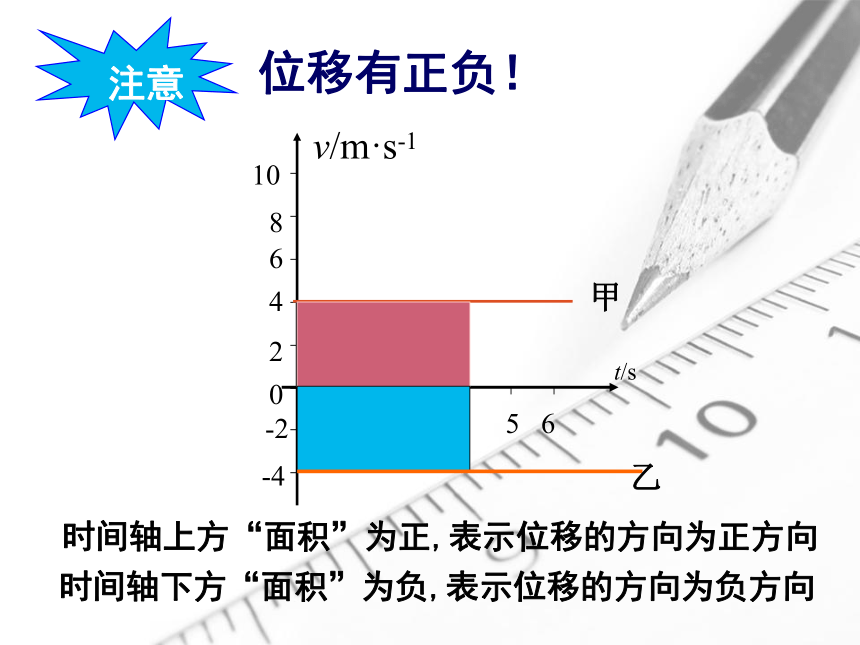
甲
-2
-4
时间轴上方“面积”为正,表示位移的方向为正方向
时间轴下方“面积”为负,表示位移的方向为负方向
乙
位移有正负!
注意
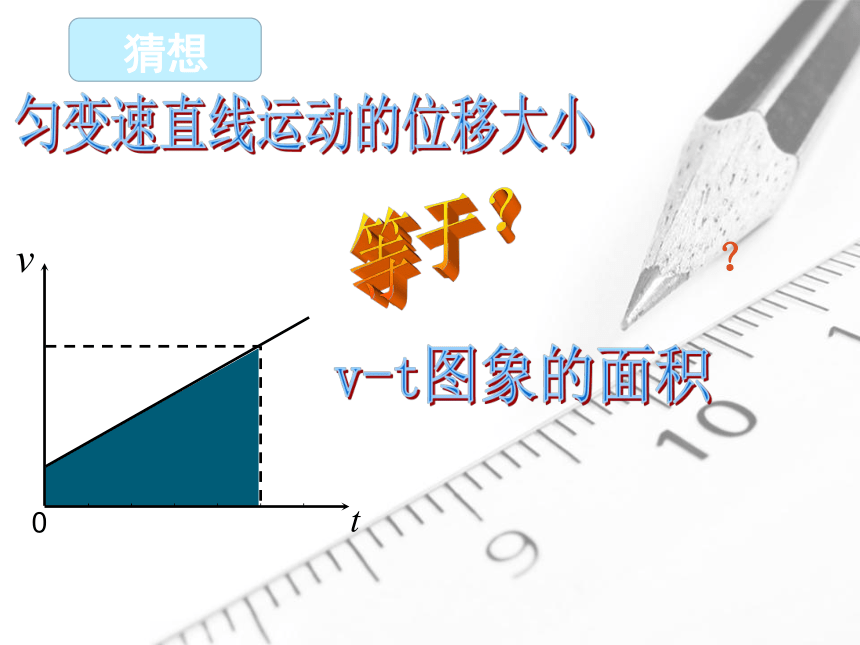
猜想
匀变速直线运动的位移大小
v-t图象的面积
等于?
?
0
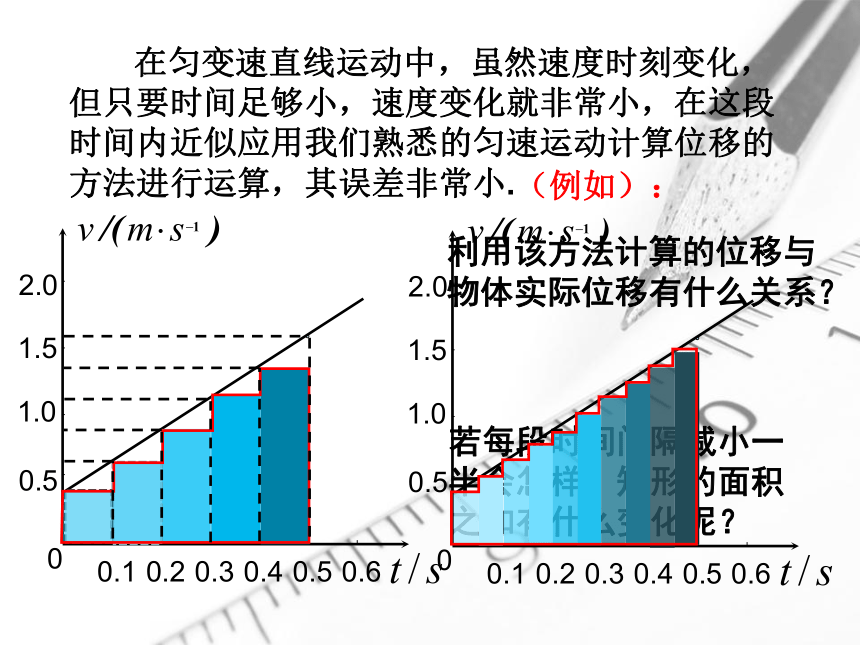
初中时我们曾经用“以直代曲”的方法,估测一段曲线的长度。
回顾:
这体现了什么科学思想?
此科学思想方法能否应用到匀变速直线运动的v-t图象上?
在匀变速直线运动中,虽然速度时刻变化,但只要时间足够小,速度变化就非常小,在这段时间内近似应用我们熟悉的匀速运动计算位移的方法进行运算,其误差非常小.
0
0.5
1.0
1.5
2.0
0.1
0.2
0.3
0.4
0.5
0.6
利用该方法计算的位移与物体实际位移有什么关系?
若每段时间间隔减小一半会怎样?矩形的面积之和有什么变化呢?
(例如):
0
0.5
1.0
1.5
2.0
0.1
0.2
0.3
0.4
0.5
0.6
0
0.5
1.0
1.5
2.0
0.1
0.2
0.3
0.4
0.5
0.6
图像和t轴围成的面积就代表了这段时间内运动的位移。
极限思想
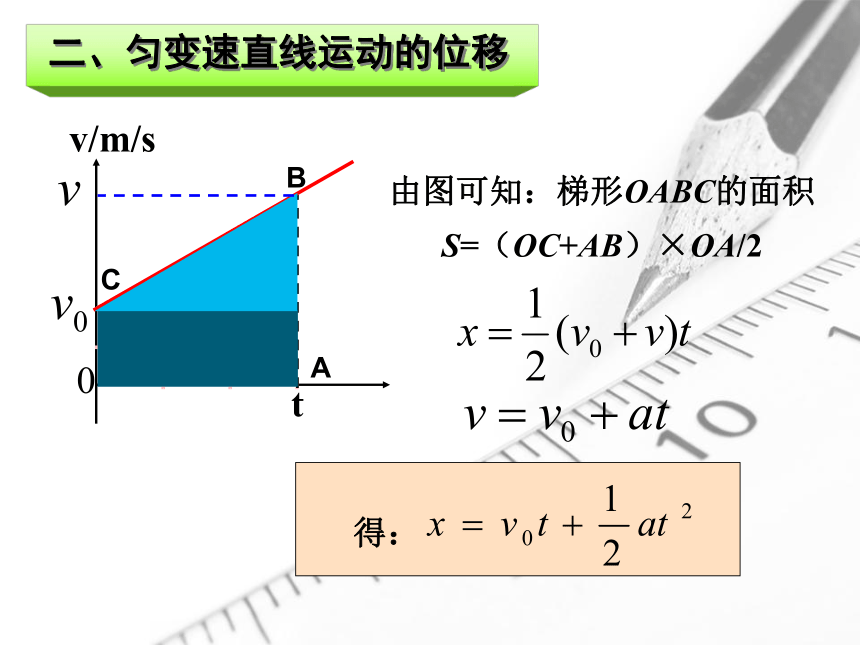
二、匀变速直线运动的位移
思想:把过程无限分割,以“不变”代替“变”,再进行累加的思想 。微元法
由图可知:梯形OABC的面积
S=(OC+AB)×OA/2
得:
t
v/m/s
0
A
B
C
二、匀变速直线运动的位移
1.位移公式:
2.对该位移公式应注意:
本公式适用于匀变速直线运动。
υ0、α、x 都是矢量(有方向),使用公式时应先规定正方向。(一般以υ0的方向为正)
代数据时,各物理量的单位要统一.(国际单位制中的主单位)
速度具有相对性,应用公式时需要选定一个惯性参考系
二、匀变速直线运动的位移
做一做:位移与时间的关系也可以用图象表示,这种图象叫做位移—时间图象,即x-t图象.运用初中数学中学到的一次函数和二次函数知识,你能画出匀加速直线运动x=v0t+ at2的x-t图象吗?(v0、a是常数)
一辆汽车以1m/s2的加速度加速行驶了12s,驶过了180m。汽车开始加速时的速度是多少?
解:以汽车运动的初速v0的方向为正方向
由
得:
先用字母代表物理量进行运算
例题1
三、匀变速直线运动的位移公式应用
一质点以一定初速度沿竖直方向抛出,得到它的速度一时间图象如图所示.试求出它在前 2 s 内的位移_________ ,后2 s内的位移_________,前4s内的位移_________ .
0
正方向
x1 = 5 m
5 m
x2 = - 5 m
- 5 m
x = 0
0
例题2
.
某一做直线运动的物体的图象如右图所示,根据图象求:
(1)物体距出发点的最远距离;
(2)前4 s物体的位移;
(3)前4 s内通过的路程.
练习
【答案】 (1)6 m (2)5 m (3)7 m
在用v-t图象来求解物体的位移和路程的问题中,要注意以下两点:
(1)速度图象和t轴所围成的面积数值等于物体位移的大小;
(2)速度图象和t轴所围成的面积的绝对值的和等于物体的路程.
解:以汽车初速方向为正方向
所以由
知车的位移
在平直公路上,一汽车的速度为15m/s。从某时刻开始刹车,在阻力作用下,汽车以2m/s2的加速度运动,问刹车后10s末车离开始刹车点多远?
例题3
对吗?
说明刹车后7.5s汽车停止运动。
知车的位移
正解:设车实际运动时间为t0,以汽车初速方向为正
由
得运动时间
所以由
刹车问题!
在平直公路上,一汽车的速度为15m/s。从某时刻开始刹车,在阻力作用下,汽车以2m/s2的加速度运动,问刹车后10s末车离开始刹车点多远?
例题3
在一段平滑的斜冰坡的中部将冰块以 8 m/s的初速度沿斜坡向上打出,设冰块与冰面间的摩擦不计,冰块在斜坡上的运动加速度恒为2 m/s2.
求:(设斜坡足够长)
(1)冰块在5 s时的速度;
(2)冰块在10 s时的位移.
答案:(1)2 m/s,沿斜面向下
(2)20m ,在出发点下方
练习
小结
一、匀速直线运动的位移
1、匀速直线运动,物体的位移对应着v-t图像中图线与时间轴所围的面积。
2、公式:S = v t
二、匀变速直线运动的位移
1、匀变速直线运动,物体的位移对应着v- t图像中图线与时间轴之间包围的梯形面积。
2、公式
补充:图像专题
(多选)某物体运动的v-t图像如图所示,根据图像可知,该物体( )
A.在0到2 s末的时间内,加速度为1 m/s2 B.在4 s末到5 s末的时间内,位移为2m C.5 s末物体的加速度方向发生改变 D.在0到6 s末的时间内,位移为6.5 m
AD
{5940675A-B579-460E-94D1-54222C63F5DA}内容种类
v-t图像
x-t图像
图像上某点的纵坐标
图线斜率
图线与时间轴所围面积
图线与坐标轴的交点
纵截距
横截距
两图线交点坐标
表示瞬时速度
表示某一时刻的位置
表示加速度
表示速度
表示位移
无意义
表示初速度
表示初始时刻的位置
表示开始运动或速度为零的时刻
表示开始运动的时刻
表示速度相同但不表示相遇,往往是距离最大或距离最小的临界点
表示相遇
(2)v-t图像和x-t图像都只能描述直线运动,不能描述曲线运动.
(1)确认是哪种图像,v-t图像还是x-t图像.
注意:(1)无论是v-t图像还是x-t图像都不是物体的运动轨迹.
运动图像的应用技巧
④拐点对应运动状态发生改变.
③交点对应速度或位置相同.
②纵截距与初速度或初始位置对应.
①斜率与加速度或速度对应.
(2)理解并熟记四个对应关系.
1.下列所给的图像中能反映做直线运动的物体回到初始位置的是( )
ACD
A
B
C
D
2.(多选)甲、乙两物体同时开始做直线运动,它们的位移-时间图像如图所示,则( )
A.甲物体做匀加速直线运动,乙物体做曲线运动 B.甲、乙两物体从同一地点出发 C.出发时乙在甲前x0处 D.甲、乙两物体有两次相遇
CD
3.甲、乙两个物体在同一时刻沿同一直线运动,它们的速度—时间图像如图所示,下列有关说法正确的是( )
A.在4~6 s内,甲、乙两物体的加速度大小相等、方向相反 B.前6 s内甲通过的路程更大 C.前4 s内甲、乙两物体的平
均速度相等 D.甲、乙两物体前两秒内
位移相同
BD
思想
一、匀速直线运动的位移
匀速直线运动的位移
v
x =
vt
5
10
0
t/s
10
5
v/m·s-1
结论:
对于匀速直线运动,物体的位移对应着v – t 图象中一块矩形的面积。
x = vt
v/m·s-1
t/s
2
6
4
10
8
3
4
5
6
0
2
1
甲
-2
-4
时间轴上方“面积”为正,表示位移的方向为正方向
时间轴下方“面积”为负,表示位移的方向为负方向
乙
位移有正负!
注意
猜想
匀变速直线运动的位移大小
v-t图象的面积
等于?
?
0
初中时我们曾经用“以直代曲”的方法,估测一段曲线的长度。
回顾:
这体现了什么科学思想?
此科学思想方法能否应用到匀变速直线运动的v-t图象上?
在匀变速直线运动中,虽然速度时刻变化,但只要时间足够小,速度变化就非常小,在这段时间内近似应用我们熟悉的匀速运动计算位移的方法进行运算,其误差非常小.
0
0.5
1.0
1.5
2.0
0.1
0.2
0.3
0.4
0.5
0.6
利用该方法计算的位移与物体实际位移有什么关系?
若每段时间间隔减小一半会怎样?矩形的面积之和有什么变化呢?
(例如):
0
0.5
1.0
1.5
2.0
0.1
0.2
0.3
0.4
0.5
0.6
0
0.5
1.0
1.5
2.0
0.1
0.2
0.3
0.4
0.5
0.6
图像和t轴围成的面积就代表了这段时间内运动的位移。
极限思想
二、匀变速直线运动的位移
思想:把过程无限分割,以“不变”代替“变”,再进行累加的思想 。微元法
由图可知:梯形OABC的面积
S=(OC+AB)×OA/2
得:
t
v/m/s
0
A
B
C
二、匀变速直线运动的位移
1.位移公式:
2.对该位移公式应注意:
本公式适用于匀变速直线运动。
υ0、α、x 都是矢量(有方向),使用公式时应先规定正方向。(一般以υ0的方向为正)
代数据时,各物理量的单位要统一.(国际单位制中的主单位)
速度具有相对性,应用公式时需要选定一个惯性参考系
二、匀变速直线运动的位移
做一做:位移与时间的关系也可以用图象表示,这种图象叫做位移—时间图象,即x-t图象.运用初中数学中学到的一次函数和二次函数知识,你能画出匀加速直线运动x=v0t+ at2的x-t图象吗?(v0、a是常数)
一辆汽车以1m/s2的加速度加速行驶了12s,驶过了180m。汽车开始加速时的速度是多少?
解:以汽车运动的初速v0的方向为正方向
由
得:
先用字母代表物理量进行运算
例题1
三、匀变速直线运动的位移公式应用
一质点以一定初速度沿竖直方向抛出,得到它的速度一时间图象如图所示.试求出它在前 2 s 内的位移_________ ,后2 s内的位移_________,前4s内的位移_________ .
0
正方向
x1 = 5 m
5 m
x2 = - 5 m
- 5 m
x = 0
0
例题2
.
某一做直线运动的物体的图象如右图所示,根据图象求:
(1)物体距出发点的最远距离;
(2)前4 s物体的位移;
(3)前4 s内通过的路程.
练习
【答案】 (1)6 m (2)5 m (3)7 m
在用v-t图象来求解物体的位移和路程的问题中,要注意以下两点:
(1)速度图象和t轴所围成的面积数值等于物体位移的大小;
(2)速度图象和t轴所围成的面积的绝对值的和等于物体的路程.
解:以汽车初速方向为正方向
所以由
知车的位移
在平直公路上,一汽车的速度为15m/s。从某时刻开始刹车,在阻力作用下,汽车以2m/s2的加速度运动,问刹车后10s末车离开始刹车点多远?
例题3
对吗?
说明刹车后7.5s汽车停止运动。
知车的位移
正解:设车实际运动时间为t0,以汽车初速方向为正
由
得运动时间
所以由
刹车问题!
在平直公路上,一汽车的速度为15m/s。从某时刻开始刹车,在阻力作用下,汽车以2m/s2的加速度运动,问刹车后10s末车离开始刹车点多远?
例题3
在一段平滑的斜冰坡的中部将冰块以 8 m/s的初速度沿斜坡向上打出,设冰块与冰面间的摩擦不计,冰块在斜坡上的运动加速度恒为2 m/s2.
求:(设斜坡足够长)
(1)冰块在5 s时的速度;
(2)冰块在10 s时的位移.
答案:(1)2 m/s,沿斜面向下
(2)20m ,在出发点下方
练习
小结
一、匀速直线运动的位移
1、匀速直线运动,物体的位移对应着v-t图像中图线与时间轴所围的面积。
2、公式:S = v t
二、匀变速直线运动的位移
1、匀变速直线运动,物体的位移对应着v- t图像中图线与时间轴之间包围的梯形面积。
2、公式
补充:图像专题
(多选)某物体运动的v-t图像如图所示,根据图像可知,该物体( )
A.在0到2 s末的时间内,加速度为1 m/s2 B.在4 s末到5 s末的时间内,位移为2m C.5 s末物体的加速度方向发生改变 D.在0到6 s末的时间内,位移为6.5 m
AD
{5940675A-B579-460E-94D1-54222C63F5DA}内容种类
v-t图像
x-t图像
图像上某点的纵坐标
图线斜率
图线与时间轴所围面积
图线与坐标轴的交点
纵截距
横截距
两图线交点坐标
表示瞬时速度
表示某一时刻的位置
表示加速度
表示速度
表示位移
无意义
表示初速度
表示初始时刻的位置
表示开始运动或速度为零的时刻
表示开始运动的时刻
表示速度相同但不表示相遇,往往是距离最大或距离最小的临界点
表示相遇
(2)v-t图像和x-t图像都只能描述直线运动,不能描述曲线运动.
(1)确认是哪种图像,v-t图像还是x-t图像.
注意:(1)无论是v-t图像还是x-t图像都不是物体的运动轨迹.
运动图像的应用技巧
④拐点对应运动状态发生改变.
③交点对应速度或位置相同.
②纵截距与初速度或初始位置对应.
①斜率与加速度或速度对应.
(2)理解并熟记四个对应关系.
1.下列所给的图像中能反映做直线运动的物体回到初始位置的是( )
ACD
A
B
C
D
2.(多选)甲、乙两物体同时开始做直线运动,它们的位移-时间图像如图所示,则( )
A.甲物体做匀加速直线运动,乙物体做曲线运动 B.甲、乙两物体从同一地点出发 C.出发时乙在甲前x0处 D.甲、乙两物体有两次相遇
CD
3.甲、乙两个物体在同一时刻沿同一直线运动,它们的速度—时间图像如图所示,下列有关说法正确的是( )
A.在4~6 s内,甲、乙两物体的加速度大小相等、方向相反 B.前6 s内甲通过的路程更大 C.前4 s内甲、乙两物体的平
均速度相等 D.甲、乙两物体前两秒内
位移相同
BD
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
