教科2003课标版必修1 第一章 运动的描述6. 匀变速直线运动位移与时间的关系 课件30张PPT
文档属性
| 名称 | 教科2003课标版必修1 第一章 运动的描述6. 匀变速直线运动位移与时间的关系 课件30张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览


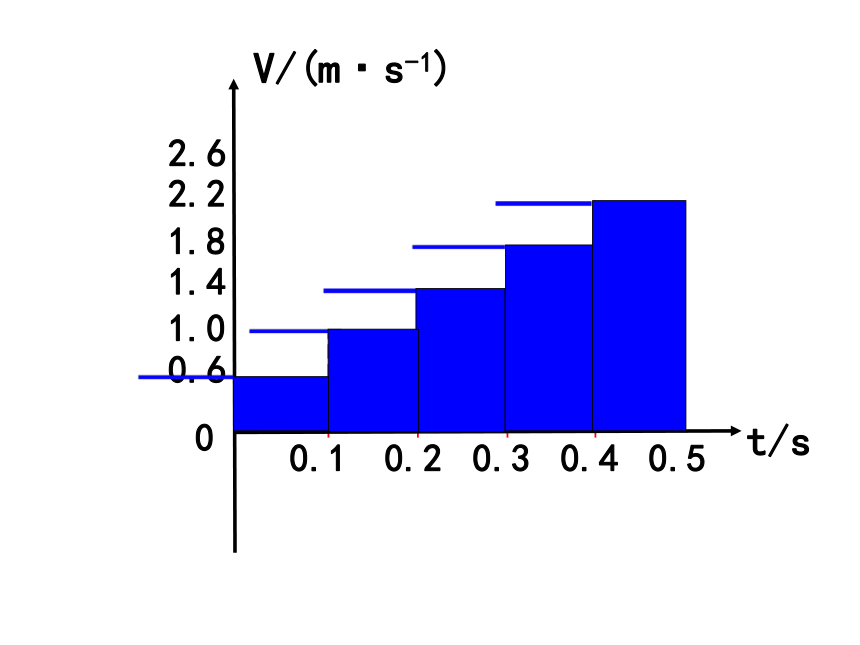

文档简介
匀变速直线运动的位移与时间
的关系
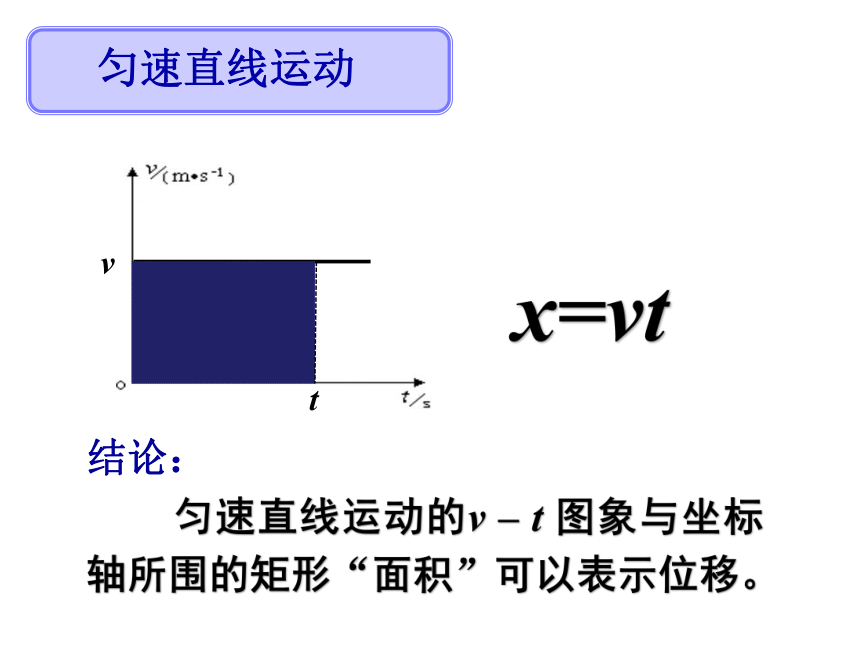
匀速直线运动
x=vt
结论:
匀速直线运动的v
–
t
图象与坐标轴所围的矩形“面积”可以表示位移。
t
v
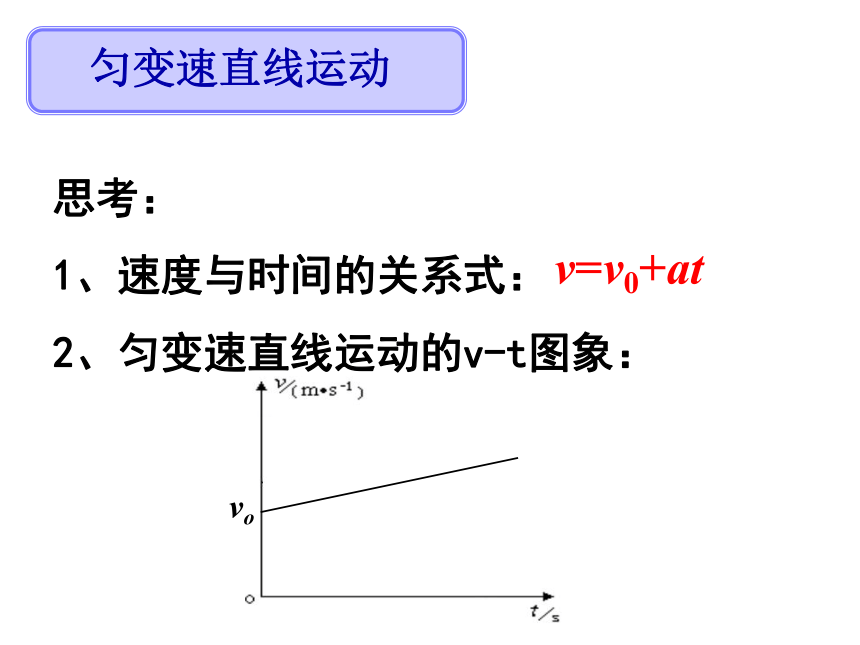
匀变速直线运动
思考:
1、速度与时间的关系式:
v=v0+at
思考:
1、速度与时间的关系式:
2、匀变速直线运动的v-t图象:
v=v0+at
vo
匀变速直线运动
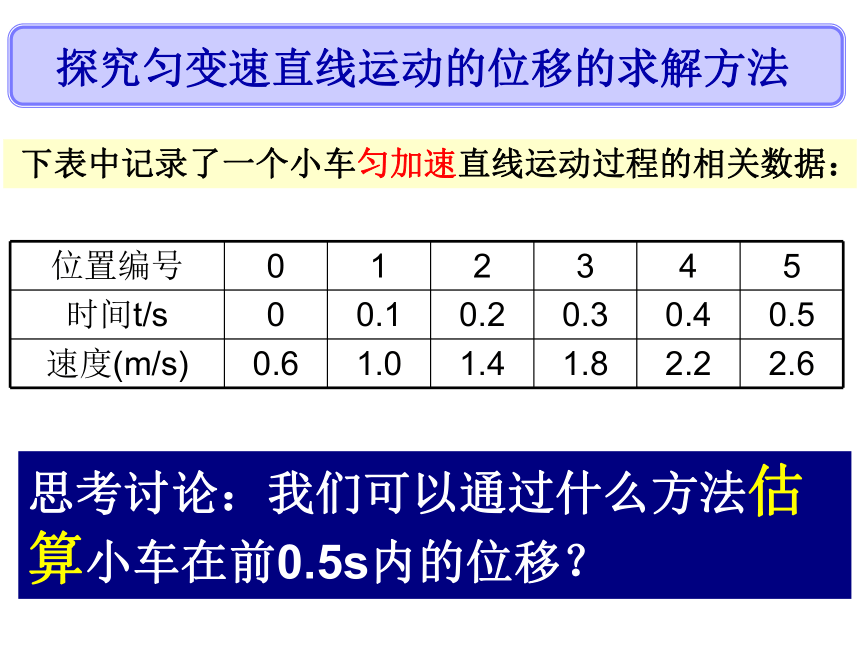
位置编号
0
1
2
3
4
5
时间t/s
0
0.1
0.2
0.3
0.4
0.5
速度(m/s)
0.6
1.0
1.4
1.8
2.2
2.6
下表中记录了一个小车匀加速直线运动过程的相关数据:
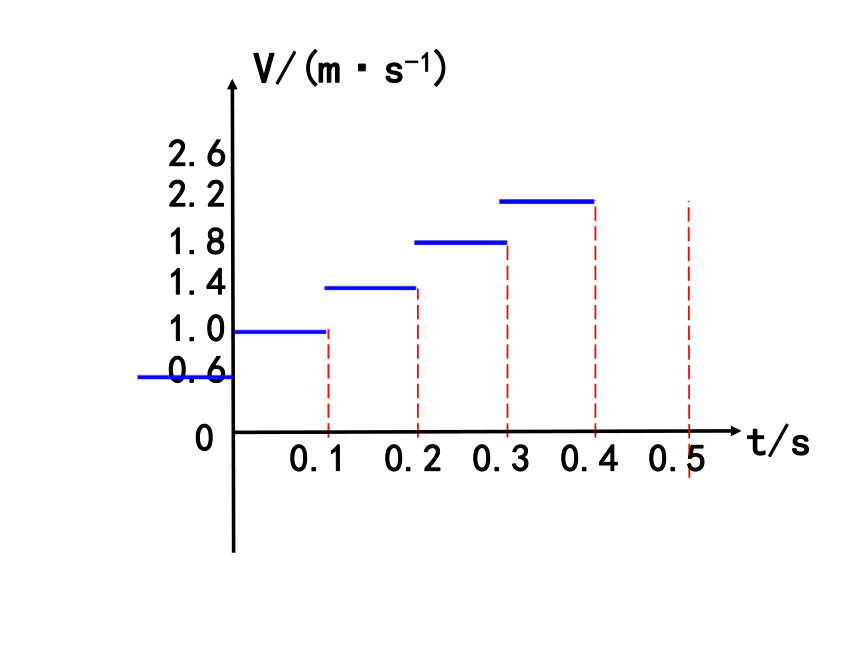
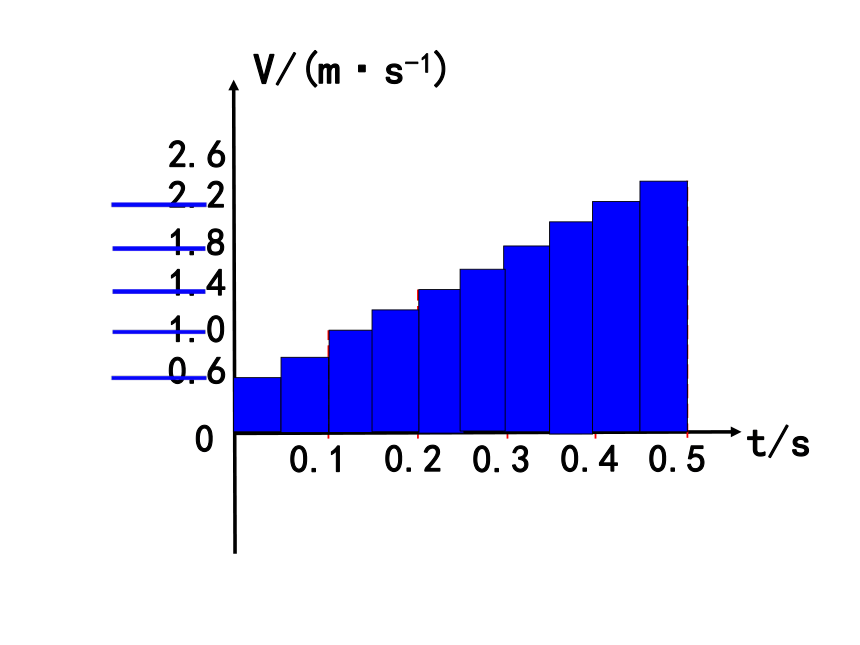
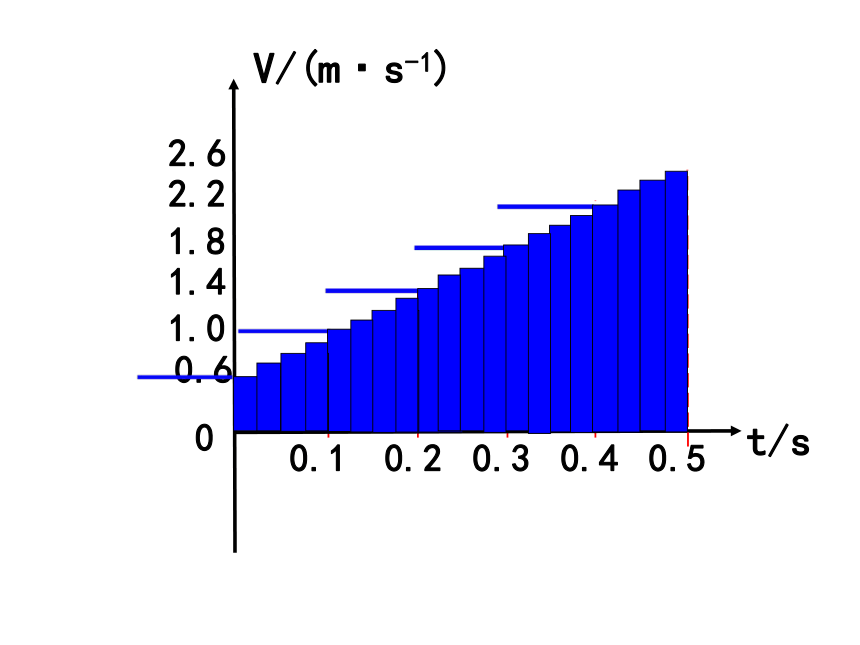
探究匀变速直线运动的位移的求解方法
思考讨论:我们可以通过什么方法估算小车在前0.5s内的位移?
2
V/(m·s-1)
0
t/s
0
0.1
0.2
0.3
0.4
0.5
0.6
1.0
1.4
1.8
2.2
2.6
2
V/(m·s-1)
0
t/s
0
0.1
0.2
0.3
0.4
0.5
0.6
1.0
1.4
1.8
2.2
2.6
2
V/(m·s-1)
0
t/s
0
0.1
0.2
0.3
0.4
0.5
0.6
1.0
1.4
1.8
2.2
2.6
2
V/(m·s-1)
0
t/s
0
0.1
0.2
0.3
0.4
0.5
0.6
1.0
1.4
1.8
2.2
2.6
2
V/(m·s-1)
0
t/s
0
0.1
0.2
0.3
0.4
0.5
0.6
1.0
1.4
1.8
2.2
2.6
2
0
t
0
V
2
V
0
t
0
2
V
0
t
0
2
V
0
t
2
0
t
0
V
2
V
0
t
0
2
V
0
t
0
2
V
0
t
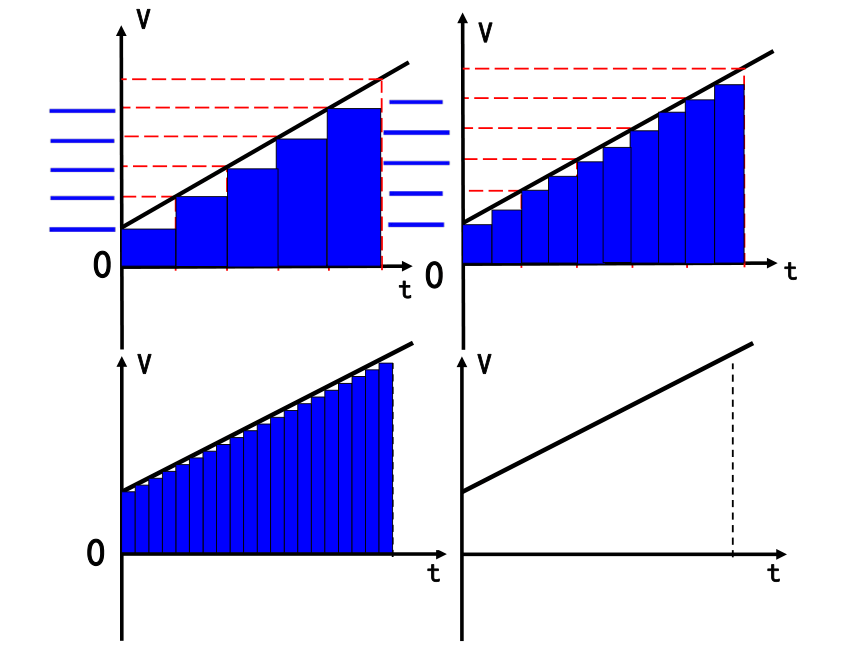
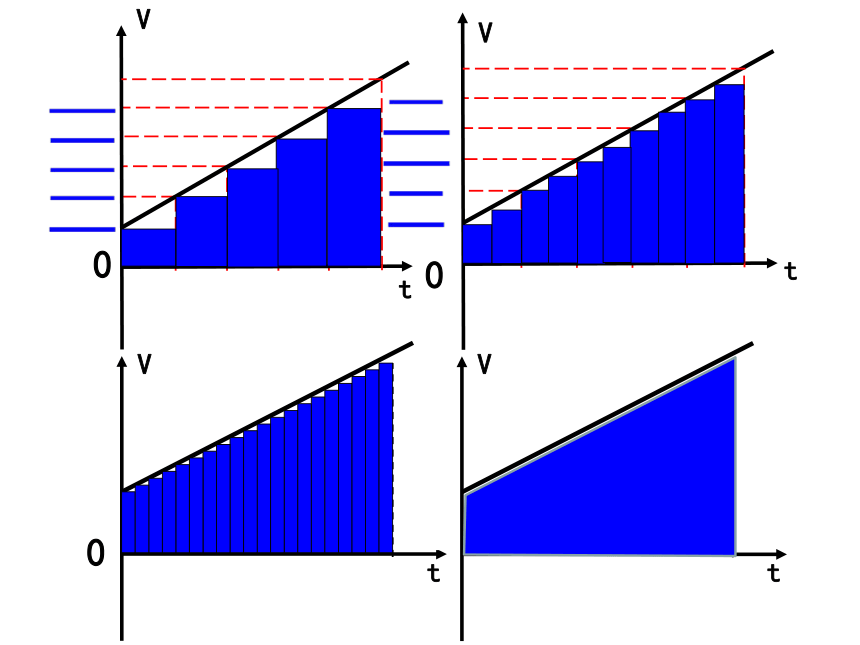
总结探究过程
随着时间被分割的份数增加到无穷多,这四个量之间的联系:
各段匀速直线
运动位移的加和
匀变速直线
运动的位移
矩形面积的加和
梯形的面积
2
V
0
t
=
=
=
=
思考与讨论
一个物体的v-t图象如下图所示,图象与坐标轴所围的面积还能表示物体的位移吗?
2
V
0
t
0
割圆术
圆周率计算上的有
所突破,有赖于有效方法的诞生,这种方法就是割圆术。刘徽经过深入研究,他发现圆内接正多边形边数无限增加时,多边形周长可无限逼近圆周长,从而创立了“割圆术”。
S=(OC+AB)×OA/2
计算公式:
v0
t
v
v
0
t
v0
匀变速直线运动的v-t图象与坐标轴围成的梯形的面积可以表示匀变速直线运动的位移。
总结探究结论
v
v
0
t
v
t
v=v0+at
匀变速直线运动的位移与时间关系
v0
实验验证
实验装置:长木板、电火花打点计时器、
墨粉纸、小车、钩码、纸带、
刻度尺、电源
实验验证
目的:由公式计算的位移=实际位移
思考:需要哪些物理量?
实验验证
v0
、v、t、x
=x测量
处理纸带:选好坐标原点,选好计数点,记录各点的位置,记录时间间隔。
描点作图:建轴、选好刻度、描点,作出匀变速直线运动的x-t图象。
实验验证
匀变速直线运动的x-t图象为抛物线
一辆汽车以1m/s2的加速度加速行驶了12s,驶过了180m。汽车开始加速时的速度是多少?
解:以汽车运动的初速度v0的方向为正方向
由
得:
先用字母代表物理量进行运算
典例精析
【思考】
1、我们研究的是哪个过程?
2、汽车做什么运动?
3、哪些量已知,要求什么量?作出运动过程示意图。
汽车开始加速时的速度是9m/s。
随堂练直公路上,汽车以54km/h的
速度匀速行驶。从某时刻开始刹车,在阻力作用下,汽车以2m/s2的加速度运动,问刹车后3s末和10s末汽车离开始刹车点多远?
2.
对位移公式的理解:
匀变速直线运动的位移与时间的关系
1.
位移公式:
2.
对位移公式的理解:
(1)反映了位移随时间的变化规律
(2)因为v0、a、x均为矢量,使用公式时
应先规定正方向
匀变速直线运动的位移与时间的关系
1.
位移公式:
(3)应用公式解题时应考虑客观事实,例
如刹车问题
(4)t是指物体运动的实际时间,与发生这
段位移对应起来
(5)代入数据时,各物理量的单位要统一
一、v-t图象面积表示位移
位移=“面积”
二、匀变速直线运动的位移与时间的关系
三、物理思想方法----微元法
小结
请用刻度尺设计一个实验测定你的反应时间,比一比谁反应更快?
比一比谁的反应快
谢谢!
的关系
匀速直线运动
x=vt
结论:
匀速直线运动的v
–
t
图象与坐标轴所围的矩形“面积”可以表示位移。
t
v
匀变速直线运动
思考:
1、速度与时间的关系式:
v=v0+at
思考:
1、速度与时间的关系式:
2、匀变速直线运动的v-t图象:
v=v0+at
vo
匀变速直线运动
位置编号
0
1
2
3
4
5
时间t/s
0
0.1
0.2
0.3
0.4
0.5
速度(m/s)
0.6
1.0
1.4
1.8
2.2
2.6
下表中记录了一个小车匀加速直线运动过程的相关数据:
探究匀变速直线运动的位移的求解方法
思考讨论:我们可以通过什么方法估算小车在前0.5s内的位移?
2
V/(m·s-1)
0
t/s
0
0.1
0.2
0.3
0.4
0.5
0.6
1.0
1.4
1.8
2.2
2.6
2
V/(m·s-1)
0
t/s
0
0.1
0.2
0.3
0.4
0.5
0.6
1.0
1.4
1.8
2.2
2.6
2
V/(m·s-1)
0
t/s
0
0.1
0.2
0.3
0.4
0.5
0.6
1.0
1.4
1.8
2.2
2.6
2
V/(m·s-1)
0
t/s
0
0.1
0.2
0.3
0.4
0.5
0.6
1.0
1.4
1.8
2.2
2.6
2
V/(m·s-1)
0
t/s
0
0.1
0.2
0.3
0.4
0.5
0.6
1.0
1.4
1.8
2.2
2.6
2
0
t
0
V
2
V
0
t
0
2
V
0
t
0
2
V
0
t
2
0
t
0
V
2
V
0
t
0
2
V
0
t
0
2
V
0
t
总结探究过程
随着时间被分割的份数增加到无穷多,这四个量之间的联系:
各段匀速直线
运动位移的加和
匀变速直线
运动的位移
矩形面积的加和
梯形的面积
2
V
0
t
=
=
=
=
思考与讨论
一个物体的v-t图象如下图所示,图象与坐标轴所围的面积还能表示物体的位移吗?
2
V
0
t
0
割圆术
圆周率计算上的有
所突破,有赖于有效方法的诞生,这种方法就是割圆术。刘徽经过深入研究,他发现圆内接正多边形边数无限增加时,多边形周长可无限逼近圆周长,从而创立了“割圆术”。
S=(OC+AB)×OA/2
计算公式:
v0
t
v
v
0
t
v0
匀变速直线运动的v-t图象与坐标轴围成的梯形的面积可以表示匀变速直线运动的位移。
总结探究结论
v
v
0
t
v
t
v=v0+at
匀变速直线运动的位移与时间关系
v0
实验验证
实验装置:长木板、电火花打点计时器、
墨粉纸、小车、钩码、纸带、
刻度尺、电源
实验验证
目的:由公式计算的位移=实际位移
思考:需要哪些物理量?
实验验证
v0
、v、t、x
=x测量
处理纸带:选好坐标原点,选好计数点,记录各点的位置,记录时间间隔。
描点作图:建轴、选好刻度、描点,作出匀变速直线运动的x-t图象。
实验验证
匀变速直线运动的x-t图象为抛物线
一辆汽车以1m/s2的加速度加速行驶了12s,驶过了180m。汽车开始加速时的速度是多少?
解:以汽车运动的初速度v0的方向为正方向
由
得:
先用字母代表物理量进行运算
典例精析
【思考】
1、我们研究的是哪个过程?
2、汽车做什么运动?
3、哪些量已知,要求什么量?作出运动过程示意图。
汽车开始加速时的速度是9m/s。
随堂练直公路上,汽车以54km/h的
速度匀速行驶。从某时刻开始刹车,在阻力作用下,汽车以2m/s2的加速度运动,问刹车后3s末和10s末汽车离开始刹车点多远?
2.
对位移公式的理解:
匀变速直线运动的位移与时间的关系
1.
位移公式:
2.
对位移公式的理解:
(1)反映了位移随时间的变化规律
(2)因为v0、a、x均为矢量,使用公式时
应先规定正方向
匀变速直线运动的位移与时间的关系
1.
位移公式:
(3)应用公式解题时应考虑客观事实,例
如刹车问题
(4)t是指物体运动的实际时间,与发生这
段位移对应起来
(5)代入数据时,各物理量的单位要统一
一、v-t图象面积表示位移
位移=“面积”
二、匀变速直线运动的位移与时间的关系
三、物理思想方法----微元法
小结
请用刻度尺设计一个实验测定你的反应时间,比一比谁反应更快?
比一比谁的反应快
谢谢!
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
