高中物理教科版必修1_ 第一章 运动的描述 _ 6. 匀变速直线运动位移与时间的关系 _课件21张PPT
文档属性
| 名称 | 高中物理教科版必修1_ 第一章 运动的描述 _ 6. 匀变速直线运动位移与时间的关系 _课件21张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览





文档简介
第二章 匀变速直线运动的研究
匀变速直线运动的速度与时间
的关系
匀变速直线运动是一种理想化的运动模型。生活中的许多运动由于受到多种因素的影响,运动规律往往比较复杂,但我们忽略某些次要因素后,有时也可以把它们看成是匀变速直线运动,例如:
在平直的高速公路上行驶的汽车,在超车的一段时间内,可以认为它做匀加速直线运动,刹车时则做匀减速直线运动,直到停止。
学点1 匀变速直线运动
⑴匀变速直线运动:沿着一条直线,且加速度不变的运动,叫做匀变速直线运动。
②特点:
速度均匀变化,即
是一个恒定值。
①分类:
匀加速直线运动:若速度是均匀增大的;
匀减速直线运动:若速度是均匀减小的。
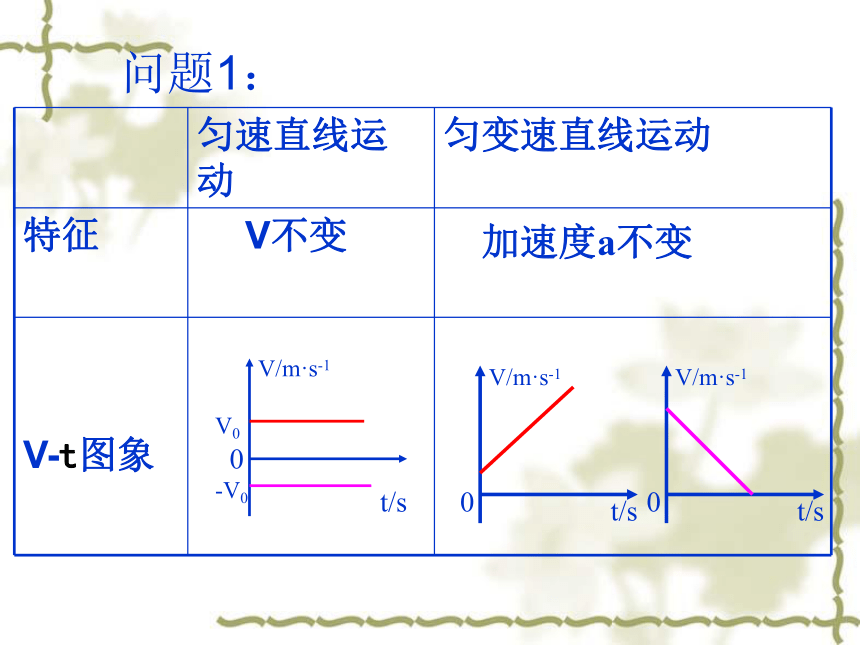
问题1:
匀速直线运动
匀变速直线运动
特征
V-t图象
V不变
加速度a不变
0
V/m·s-1
t/s
V0
-V0
V/m·s-1
t/s
0
V/m·s-1
t/s
0
【例1】关于直线运动,下列说法中正确的是( )
A.匀速直线运动的速度是恒定的,不随时间改变
B.匀变速直线运动的瞬时速度随时间改变
C.速度随时间不断增加的运动,叫匀加速直线运动
D.速度随时间均匀减小的运动,通常叫做匀减速直线运动
ABD
【答案】⑴16 m ⑵10 m ⑶22 m
1
某物体做直线运动的v-t图象如图2-2-4所示。求:
⑴前4 s的位移x1;
⑵前7 s的位移x2;
⑶前7 s内的路程。
图2-2-4
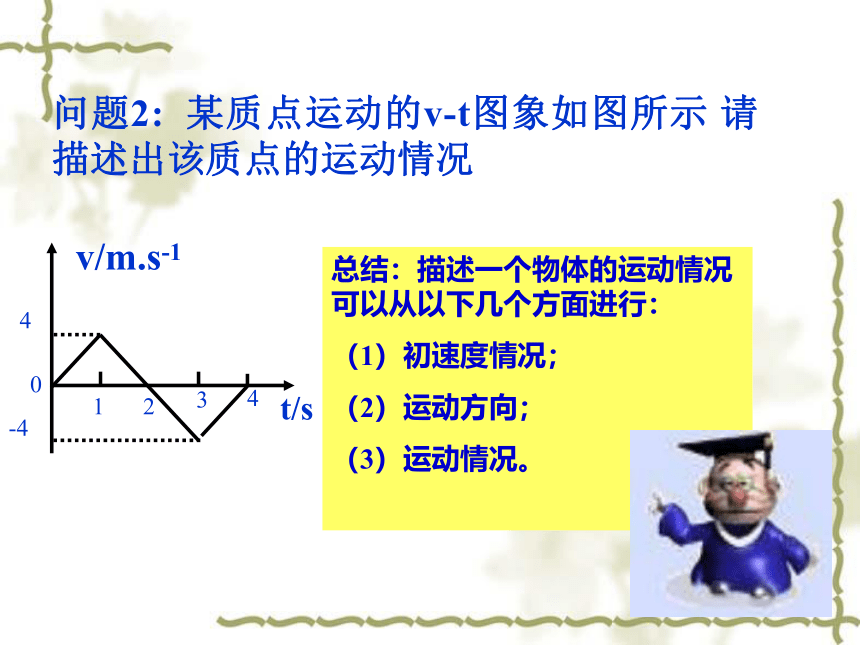
问题2: 某质点运动的v-t图象如图所示 请描述出该质点的运动情况
t/s
1
2
3
4
v/m.s-1
4
-4
0
总结:描述一个物体的运动情况可以从以下几个方面进行:
(1)初速度情况;
(2)运动方向;
(3)运动情况。
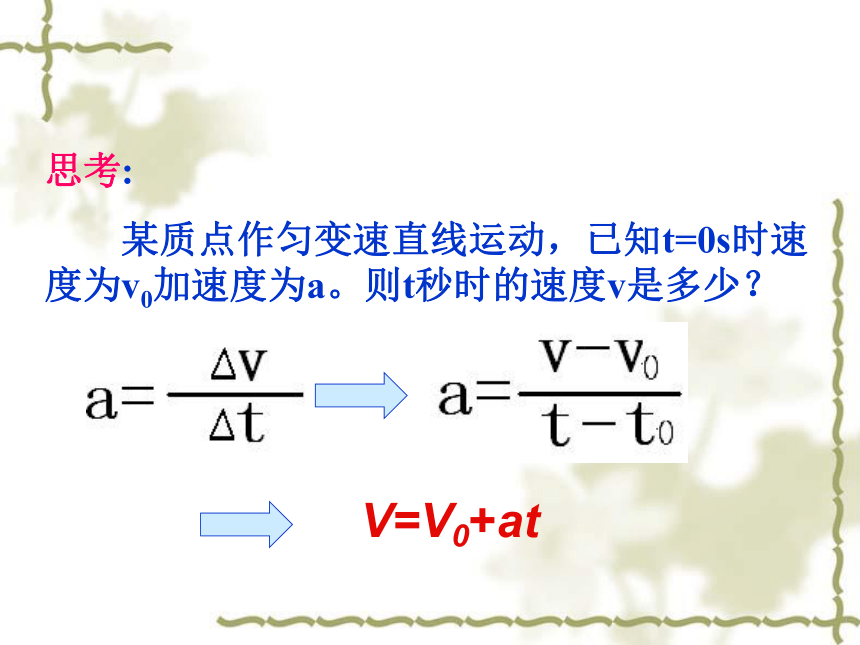
思考:
某质点作匀变速直线运动,已知t=0s时速度为v0加速度为a。则t秒时的速度v是多少?
V=V0+at
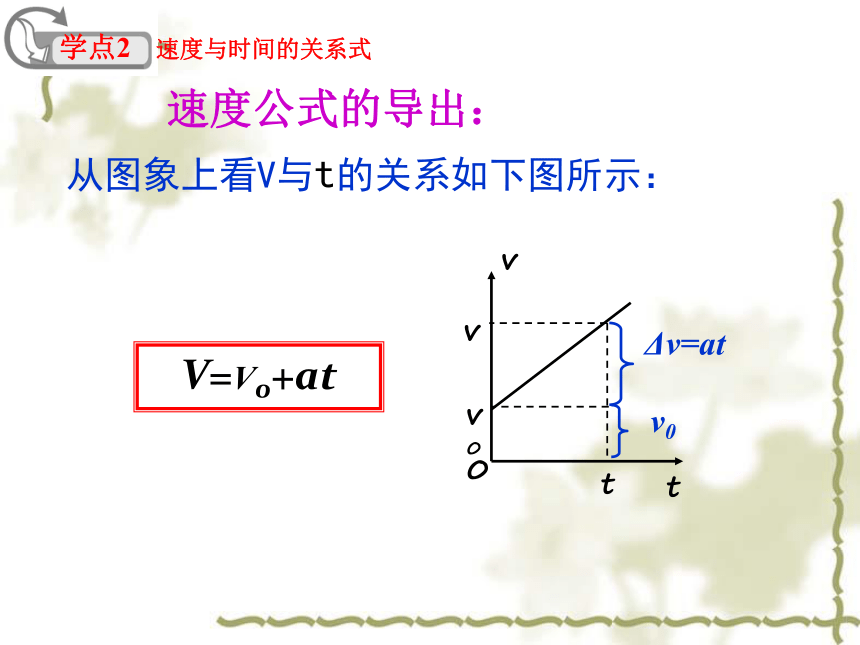
学点2 速度与时间的关系式
速度公式的导出:
v0
t
v
t
v
0
Δv=at
v0
V=V0+at
从图象上看V与t的关系如下图所示:
注意:
1、该式是矢量式(应用时要先规定正方向);
2、刹车问题要先判断停止时间。
2
10
4
t/s
v/ms-1
0
不能!该式只适用于匀变速直线运动!
问题5:某质点运动的v-t图象如下图所示, 已知t=2s时速度v0=10m/s,加速度a=2m/s2。能否利用公式v=vo+at求出4s时的速度?
(1) V=V0+at只适用于匀变速直线运动。
(2) 适用于任意的运动,包括直
线和曲线
提醒:V=V0+at和
适用条件不同:
问题3: 某质点作匀加速直线运动, v0=10m/s,加速度a=3m/s2,则该质点在3秒末的速度为多少?
已知:设初速度方向为正,v0=10m/s, a=3m/s2,t=3s
求:v
解:根据速度公式v=vo+at,代入数据,
质点在3s末的速度为v=v0+at=10m/s+3×3m/s=19m/s
问题4:汽车以20m/s的速度匀速行驶,现以4.0m/s2的加速度开始刹车,则刹车后3s末和6s末的速度各是多少?
解答1:
已知:设初速度方向为正, v0=20m/s
a=﹣4.0m/s2,
求:v3,v6
解:由速度公式v=vo+at,
可知刹车后3s末的速度
v3=v0+at=20m/s﹣4.0×3m/s=8m/s
6s末的速度
v6=v0+at=20m/s﹣4.0×6m/s=-4m/s
解答2:
已知:v0=20m/s a=﹣4.0m/s2,
求:v3,v6
解:由速度公式v=vo+at,
可知刹车后3s末的速度
v3=v0+at=20m/s﹣4.0×3m/s=8m/s
由速度公式v=vo+at
刹车至停止所需时间t =(v﹣v0)/a
=(0﹣20)/﹣4.0
=5s
故刹车后6s时v6=0
美“肯尼迪”号航空母舰上装有帮助飞机起飞的弹射系统。已知“F-15”型战斗机在跑道上加速时产生的最大加速度为5.0m/s2,起飞的最小速度是50 m/s,弹射系统能够使飞机所具有的最大速度为30m/s,则飞机起飞时在跑道上至少加速多长时间才能起飞?
1
公式v=v0+at是矢量式,如果我们取v0的方向为正方向,当物体做匀加速直线运动时,a取正号,得到的末速度v也为正。当物体做匀减速运动时,a取负号,得到的末速度v可能为正,也可能为负。如果为正,说明末速度与初速度方向相同;如果为负,说明末速度与初速度方向相反。
1.公式v=v0+at是匀变速直线运动的速度和时间的关系式,而匀变速运动有匀加速和匀减速两种运动,两种运动如何应用同一个关系式?
在匀减速直线运动中,若取v0的方向为正方向,则a为负值。当时间t较大时,末速度可能为负,而负值是否符合实际,则需要进行分析。例如汽车刹车时,初速度为10 m/s,加速度a=-2 m/s2,5 s后速度就变为零了。但有的同学却求出7 s时的速度v=v0+at=10 m/s+(-2)×7 m/s=-4 m/s。这显然是汽车刹车后又以相同的加速度倒车,与实际是不相符的。出现这些错误,不是公式有问题,而是我们没有明确v=v0+at只适用于匀变速直线运动。刹车过程的匀减速运动与刹车后的“静止”已经不是同一个运动了。
2.应用v=v0+at求解匀减速运动的实际问题时应注意哪些事项?
图象Ⅰ表示质点沿正方向做减速运动,其加速度为a1=74 m/s2。
图象Ⅱ表示质点沿正方向做匀加速直线运动,初速度为5 m/s,加速度为a2=1.25 m/s2。
图象Ⅲ表示质点沿正方向先做初速度为零的加速度逐渐减小的加速运动,8 s后做速度为16 m/s的匀速直线运动。
图象Ⅳ表示质点在前4 s内沿正方向做加速度逐渐减小的减速运动,4 s后做速度为4 m/s的匀速直线运动.
如图2-2-5所示的四条v-t图象分别表示了什么样的运动?
图2-2-5
退出
匀变速直线运动的速度与时间
的关系
匀变速直线运动是一种理想化的运动模型。生活中的许多运动由于受到多种因素的影响,运动规律往往比较复杂,但我们忽略某些次要因素后,有时也可以把它们看成是匀变速直线运动,例如:
在平直的高速公路上行驶的汽车,在超车的一段时间内,可以认为它做匀加速直线运动,刹车时则做匀减速直线运动,直到停止。
学点1 匀变速直线运动
⑴匀变速直线运动:沿着一条直线,且加速度不变的运动,叫做匀变速直线运动。
②特点:
速度均匀变化,即
是一个恒定值。
①分类:
匀加速直线运动:若速度是均匀增大的;
匀减速直线运动:若速度是均匀减小的。
问题1:
匀速直线运动
匀变速直线运动
特征
V-t图象
V不变
加速度a不变
0
V/m·s-1
t/s
V0
-V0
V/m·s-1
t/s
0
V/m·s-1
t/s
0
【例1】关于直线运动,下列说法中正确的是( )
A.匀速直线运动的速度是恒定的,不随时间改变
B.匀变速直线运动的瞬时速度随时间改变
C.速度随时间不断增加的运动,叫匀加速直线运动
D.速度随时间均匀减小的运动,通常叫做匀减速直线运动
ABD
【答案】⑴16 m ⑵10 m ⑶22 m
1
某物体做直线运动的v-t图象如图2-2-4所示。求:
⑴前4 s的位移x1;
⑵前7 s的位移x2;
⑶前7 s内的路程。
图2-2-4
问题2: 某质点运动的v-t图象如图所示 请描述出该质点的运动情况
t/s
1
2
3
4
v/m.s-1
4
-4
0
总结:描述一个物体的运动情况可以从以下几个方面进行:
(1)初速度情况;
(2)运动方向;
(3)运动情况。
思考:
某质点作匀变速直线运动,已知t=0s时速度为v0加速度为a。则t秒时的速度v是多少?
V=V0+at
学点2 速度与时间的关系式
速度公式的导出:
v0
t
v
t
v
0
Δv=at
v0
V=V0+at
从图象上看V与t的关系如下图所示:
注意:
1、该式是矢量式(应用时要先规定正方向);
2、刹车问题要先判断停止时间。
2
10
4
t/s
v/ms-1
0
不能!该式只适用于匀变速直线运动!
问题5:某质点运动的v-t图象如下图所示, 已知t=2s时速度v0=10m/s,加速度a=2m/s2。能否利用公式v=vo+at求出4s时的速度?
(1) V=V0+at只适用于匀变速直线运动。
(2) 适用于任意的运动,包括直
线和曲线
提醒:V=V0+at和
适用条件不同:
问题3: 某质点作匀加速直线运动, v0=10m/s,加速度a=3m/s2,则该质点在3秒末的速度为多少?
已知:设初速度方向为正,v0=10m/s, a=3m/s2,t=3s
求:v
解:根据速度公式v=vo+at,代入数据,
质点在3s末的速度为v=v0+at=10m/s+3×3m/s=19m/s
问题4:汽车以20m/s的速度匀速行驶,现以4.0m/s2的加速度开始刹车,则刹车后3s末和6s末的速度各是多少?
解答1:
已知:设初速度方向为正, v0=20m/s
a=﹣4.0m/s2,
求:v3,v6
解:由速度公式v=vo+at,
可知刹车后3s末的速度
v3=v0+at=20m/s﹣4.0×3m/s=8m/s
6s末的速度
v6=v0+at=20m/s﹣4.0×6m/s=-4m/s
解答2:
已知:v0=20m/s a=﹣4.0m/s2,
求:v3,v6
解:由速度公式v=vo+at,
可知刹车后3s末的速度
v3=v0+at=20m/s﹣4.0×3m/s=8m/s
由速度公式v=vo+at
刹车至停止所需时间t =(v﹣v0)/a
=(0﹣20)/﹣4.0
=5s
故刹车后6s时v6=0
美“肯尼迪”号航空母舰上装有帮助飞机起飞的弹射系统。已知“F-15”型战斗机在跑道上加速时产生的最大加速度为5.0m/s2,起飞的最小速度是50 m/s,弹射系统能够使飞机所具有的最大速度为30m/s,则飞机起飞时在跑道上至少加速多长时间才能起飞?
1
公式v=v0+at是矢量式,如果我们取v0的方向为正方向,当物体做匀加速直线运动时,a取正号,得到的末速度v也为正。当物体做匀减速运动时,a取负号,得到的末速度v可能为正,也可能为负。如果为正,说明末速度与初速度方向相同;如果为负,说明末速度与初速度方向相反。
1.公式v=v0+at是匀变速直线运动的速度和时间的关系式,而匀变速运动有匀加速和匀减速两种运动,两种运动如何应用同一个关系式?
在匀减速直线运动中,若取v0的方向为正方向,则a为负值。当时间t较大时,末速度可能为负,而负值是否符合实际,则需要进行分析。例如汽车刹车时,初速度为10 m/s,加速度a=-2 m/s2,5 s后速度就变为零了。但有的同学却求出7 s时的速度v=v0+at=10 m/s+(-2)×7 m/s=-4 m/s。这显然是汽车刹车后又以相同的加速度倒车,与实际是不相符的。出现这些错误,不是公式有问题,而是我们没有明确v=v0+at只适用于匀变速直线运动。刹车过程的匀减速运动与刹车后的“静止”已经不是同一个运动了。
2.应用v=v0+at求解匀减速运动的实际问题时应注意哪些事项?
图象Ⅰ表示质点沿正方向做减速运动,其加速度为a1=74 m/s2。
图象Ⅱ表示质点沿正方向做匀加速直线运动,初速度为5 m/s,加速度为a2=1.25 m/s2。
图象Ⅲ表示质点沿正方向先做初速度为零的加速度逐渐减小的加速运动,8 s后做速度为16 m/s的匀速直线运动。
图象Ⅳ表示质点在前4 s内沿正方向做加速度逐渐减小的减速运动,4 s后做速度为4 m/s的匀速直线运动.
如图2-2-5所示的四条v-t图象分别表示了什么样的运动?
图2-2-5
退出
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
