高中物理教科版必修1_4. 速度变化快慢的描述——加速度课件55张PPT
文档属性
| 名称 | 高中物理教科版必修1_4. 速度变化快慢的描述——加速度课件55张PPT |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-28 13:19:18 | ||
图片预览


文档简介
械运动,必须另选一个物体或内部无相对运动的物
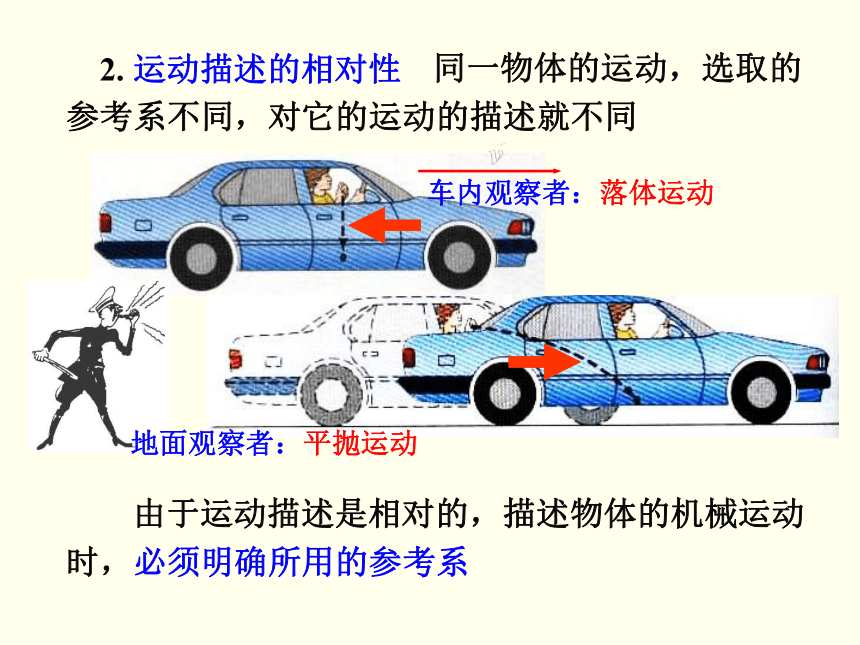
§1-1 参考系 坐标系
1. 运动的绝对性
太阳表面的运动
太阳随银河系运动
地球自转
绝对静止的物体是没有的
为了确定一个物体的位置和描述一个物体的机
体组作参考,然后研究这一物体相对于选作参考的
参考系
物体的运动,这个被选作参考的物体称为
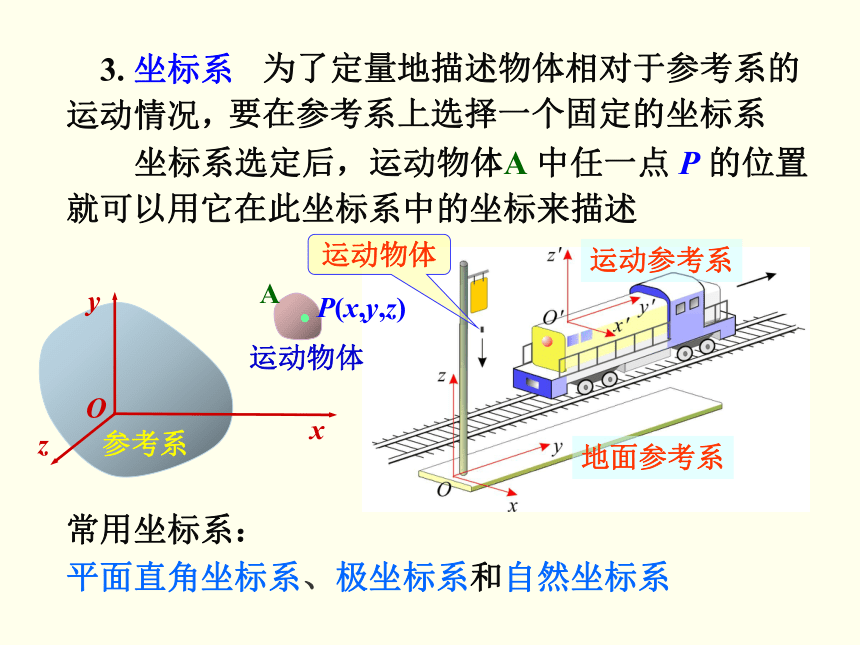
2. 运动描述的相对性
由于运动描述是相对的,描述物体的机械运动
车内观察者:落体运动
地面观察者:平抛运动
参考系不同,对它的运动的描述就不同
同一物体的运动,选取的
时,必须明确所用的参考系
要在参考系上选择一个固定的坐标系
常用坐标系:
就可以用它在此坐标系中的坐标来描述
O
x
z
y
参考系
A
P(x,y,z)
运动物体
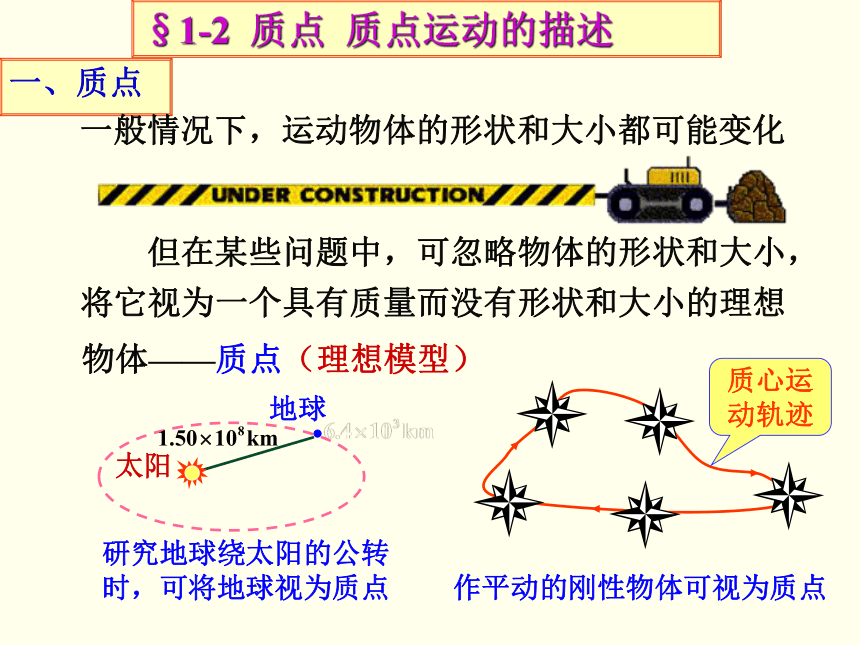
3. 坐标系
为了定量地描述物体相对于参考系的
坐标系选定后,运动物体A 中任一点 P 的位置
平面直角坐标系、极坐标系和自然坐标系
运动物体
地面参考系
运动参考系
运动情况,
一、质点
一般情况下,运动物体的形状和大小都可能变化
将它视为一个具有质量而没有形状和大小的理想
太阳
地球
研究地球绕太阳的公转时,可将地球视为质点
作平动的刚性物体可视为质点
质心运动轨迹
但在某些问题中,可忽略物体的形状和大小,
物体——质点(理想模型)
§1-2 质点 质点运动的描述
时间和时刻
时刻
时间
运行时间
出发时刻 t1
到达时刻 t2
质点运动时,它经过的某一位置对应于某一时刻
质点所走过的某一段路程,对应于某一时间间隔
二、质点运动的描述 矢量法
如何确定质点的空间位置?
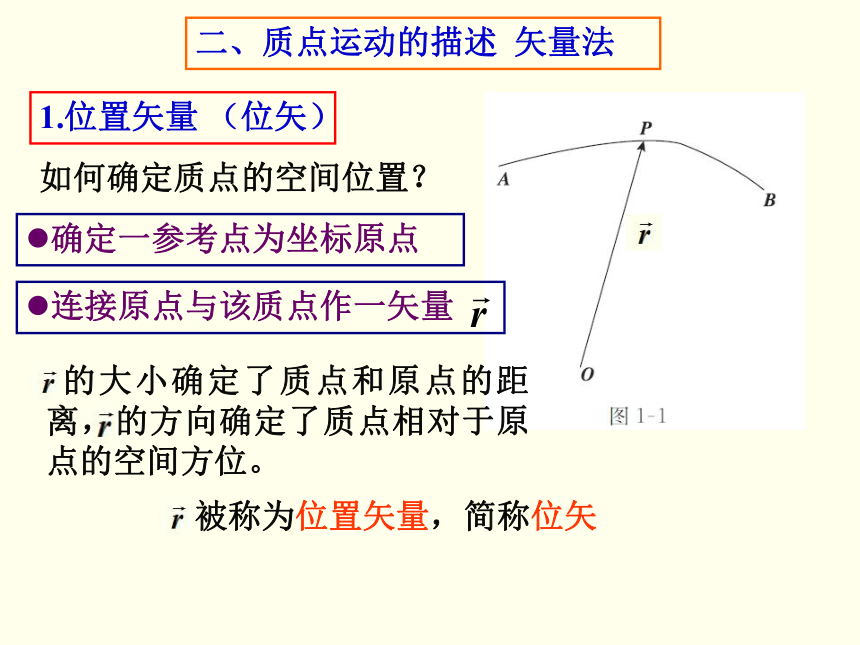
1.位置矢量 (位矢)
确定一参考点为坐标原点
连接原点与该质点作一矢量
的大小确定了质点和原点的距离,的方向确定了质点相对于原点的空间方位。
被称为位置矢量,简称位矢
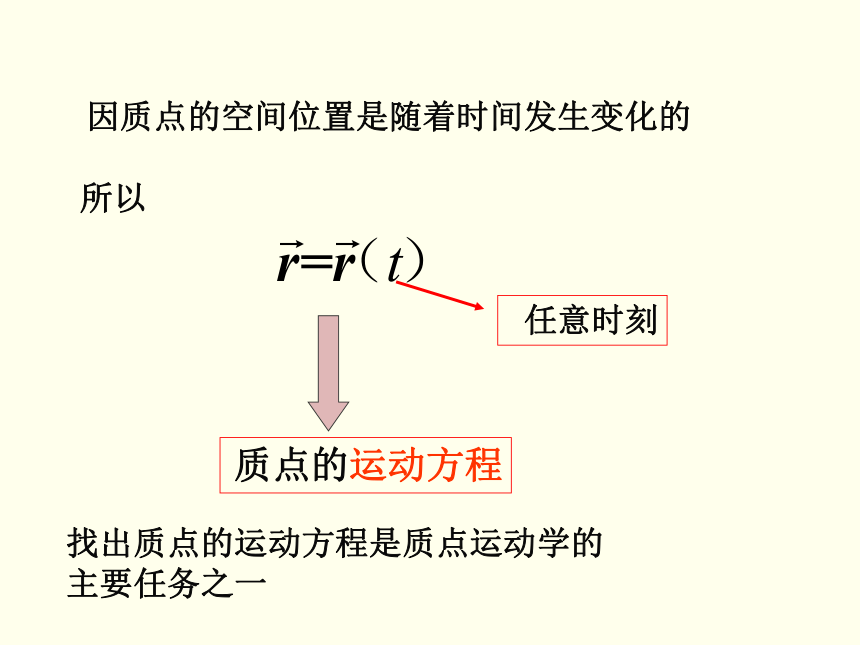
因质点的空间位置是随着时间发生变化的
所以
任意时刻
质点的运动方程
找出质点的运动方程是质点运动学的
主要任务之一
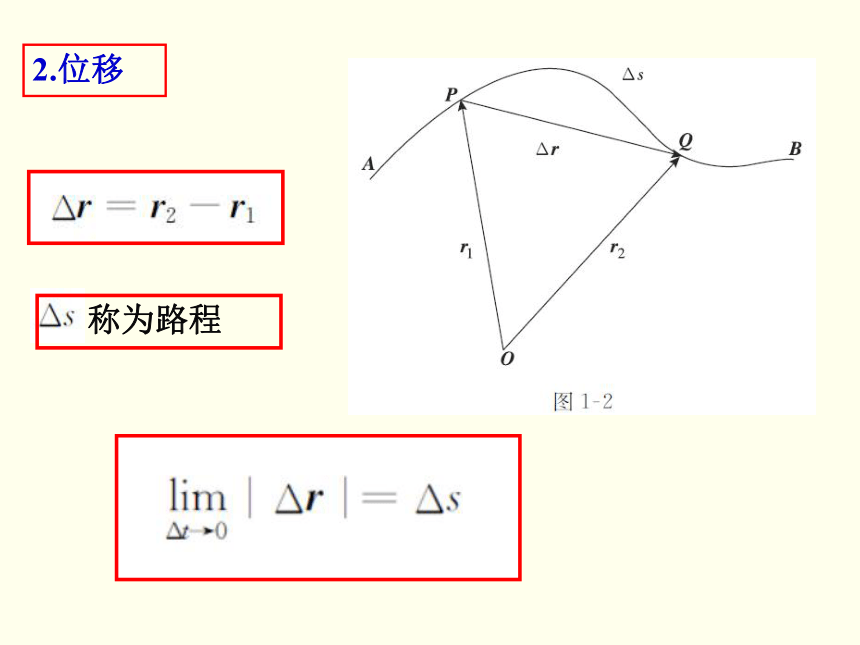
2.位移
称为路程
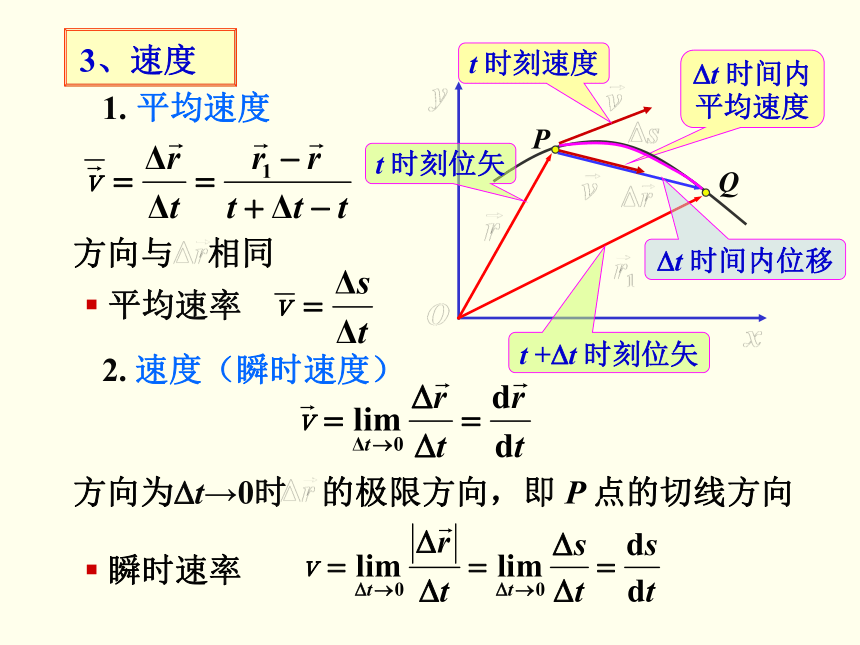
3、速度
1. 平均速度
方向与 相同
2. 速度(瞬时速度)
?t 时间内平均速度
t 时刻位矢
t +?t 时刻位矢
?t 时间内位移
P
Q
t 时刻速度
方向为?t→0时 的极限方向,即 P 点的切线方向
平均速率
瞬时速率
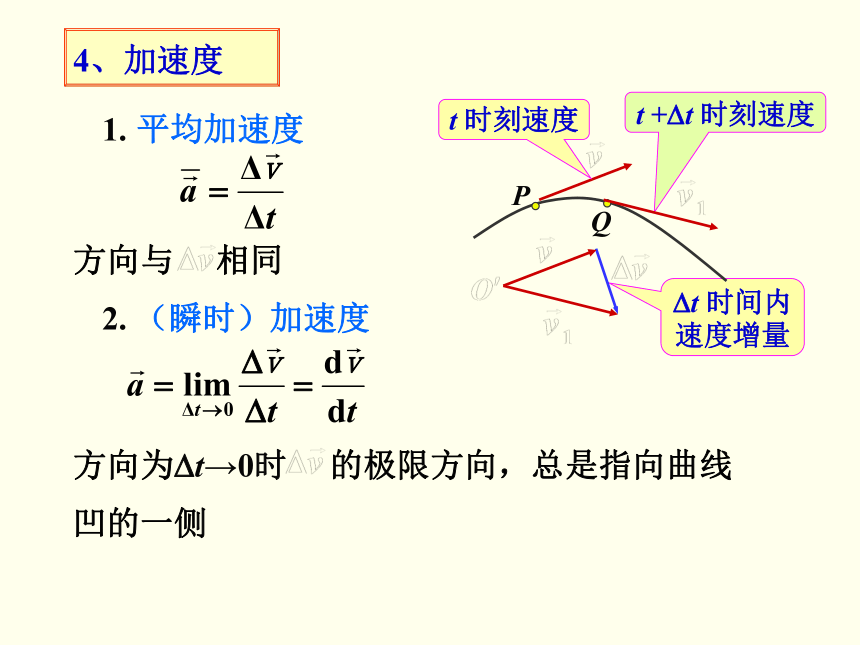
4、加速度
1. 平均加速度
2. (瞬时)加速度
?t 时间内速度增量
t +?t 时刻速度
P
Q
t 时刻速度
方向与 相同
方向为?t→0时 的极限方向,总是指向曲线
凹的一侧
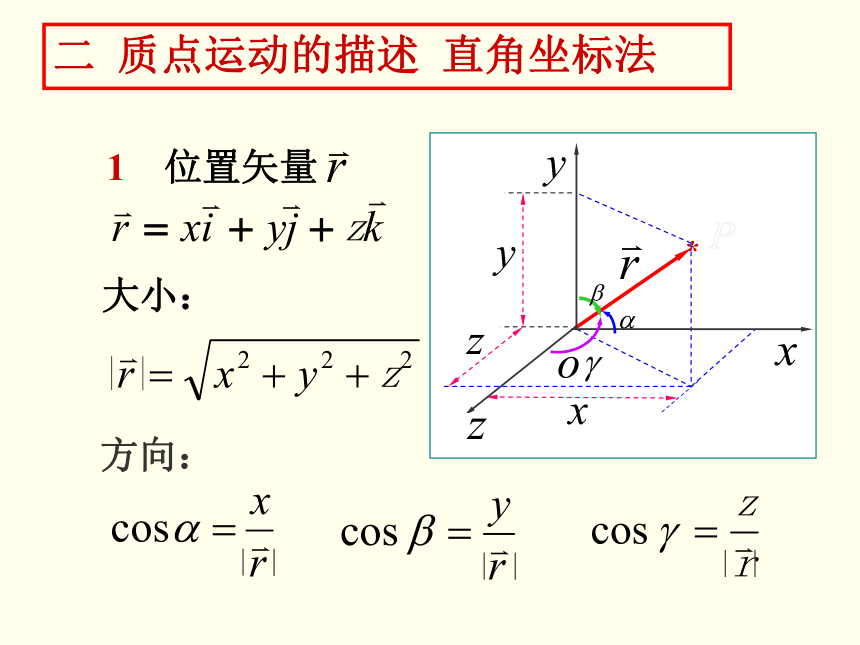
二 质点运动的描述 直角坐标法
1 位置矢量
*
方向:
大小:
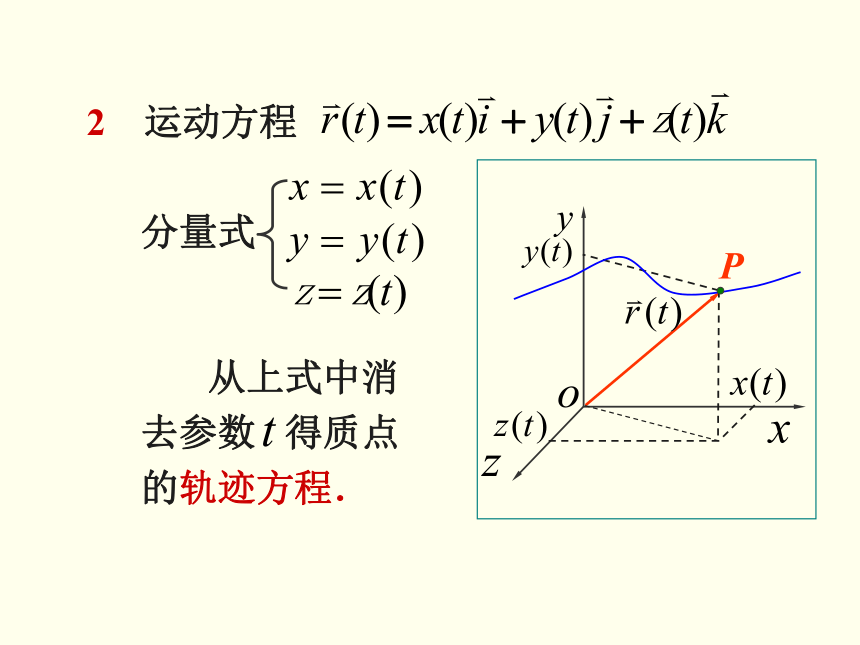
分量式
从上式中消去参数 得质点的轨迹方程.
2 运动方程
P
3 位移
平面运动:
B
A
三维运动:
4 路程( )
从P1到P2:
路程
(3) 位移是矢量,路程是标量.
位移与路程的区别
(1) 两点间位移是唯一的.
(2) 一般情况 .
注意
的意义不同.
, ,
三 速度
1 平均速度
在 时间内,质点位移为
B
A
s
D
2 瞬时速度(简称速度)
若质点在三维空间中运动,其速度
1 平均加速度
B
与 同方向
反映速度大小和方向随时间变化快慢的物理量
四 加速度
A
2 (瞬时)加速度
加速度大小
加速度方向
曲线运动 指向凹侧
直线运动
说明:矢量性
瞬时性
相对性
一运动质点在某瞬时位于位矢 的端点处,其速度大小为
(A)
(B)
(C)
(D)
讨论
注意
例1-1 某质点沿x轴方向运动,位置与时间的关系为
(SI)。试求(1)第1秒内和第3秒内的
平均速度;(2)质点在第1秒末和第3秒末的速度
和加速度。
解
(1)
时,
;
时,
则第1秒内的位移
第1秒内的平均速度大小为
方向沿x轴正向
(SI)。试求(1)第1秒内和第3秒内的
平均速度;(2)质点在第1秒末和第3秒末的速度
和加速度。
第3秒内的平均速度大小为
解
方向沿x轴负向
(1)
(2)
第1秒末的速度大小
第3秒末的速度大小
方向沿x轴负向
方向沿x轴负向
(2)
求导
求导
积分
积分
质点运动学两类基本问题
一 由质点的运动方程可以求得质点在任一时刻的位矢、速度和加速度;
二 已知质点的加速度以及初始速度和初始位置, 可求质点速度及其运动方程.
四 质点运动的描述 自然法
曲线运动
圆周运动
(1)匀速率圆周运动 向心加速度
?t 时间内速度增量为
A
B
t 时刻速度
t +?t 时刻速度
?t 时间内速度增量
加速度为
当 时加速度大小为
方向沿半径指向圆心,称为向心(法向)加速度
圆周运动
(2)变速圆周运动 切向加速度和法向加速度
速度增量分解为
速度增量的分解
A
B
t 时刻速度
t +?t 时刻速度
?t 时间内速度增量
瞬时加速度为
法向加速度
方向 沿半径指向圆心
大小
切向加速度
方向 与瞬时速度方向平行
大小
反映速度方向改变
反映速度大小变化
总加速度
与瞬时速度方向之间的夹角
大小
?
2、一般曲线运动 自然法
以轨道上任一点O为参考点,质点所在的位置P点到
O点的轨道长度s称为自然坐标
1,自然坐标s是标量
2,s可正可负
(1)自然坐标系 自然坐标
(2)速度在自然坐标系下的表示
质点在 P 点附近轨道弧元上的运动可视为在
法向加速度
切向加速度
曲率圆
总加速度
切向加速度大小
法向加速度大小
曲线于 P 点的曲率半径
t
a
曲率圆上的运动。
(3)加速度在自然坐标系下的表示
指向曲线凹的一侧
方向由 的数值决定
方向一致
方向相反
例题1-6 物体被抛出后到达 P点时,速度 与
解 不考虑空气阻力,物体的总加速度为
始终垂直于速度方向并指向抛物线凹的一侧
与速度方向相同
若 P 点位于最高点的右边,
若P 点位于最高点的左边,
与速度方向相反
P点的曲率半径,并给出曲率半径最小值。
时的切向加速度、法向加速度;(2)运动轨道在
水平方向成q 角,若忽略空气阻力,求物体在 P点
方向竖直向下
结果表明,斜抛物体达到最高点时, ,其切向
可得 P 点的曲率半径
P
O x
y
得切向加速度和法向速度的大小分别为
加速度为零,法向加速度有最大值,而轨道曲率半
径达到最小值
一 经典力学时空观
§1-3 相对运动
地面上的人测得
车上的人测得
经典力学时空观认为:
、
不依赖与观察者所在的参考系
时间和长度的绝对性是经典力学或牛顿力学的基础.
实际上时间和空间的测量是依赖于参考系的相对运动速度,但速度远小于光速时,测量结果的差异可以忽略。
经典力学时空观
时间和长度是绝对的
位矢、位移、速度、
加速度、运动轨迹都
是相对的
物体运动的轨迹依赖于观察者所处的参考系
二、相对运动
运动物体的位矢、速度、加速度、运动轨迹是相对
于某一参考系而言的,不同的参考系(观测者)因
本身的运动状态,对同一质点的测量结果可能不一样。
物体运动的轨迹依赖于观察者所处的参考系
本身的运
运动参考系 S'
静止参考系 S
由矢量加法原理有
运动质点在两参考系中位矢间的关系
运动质点
P
静止参考系 S
运动参考系 S'
速度和加速度合成定理
绝对速度=相对速度+牵连速度
速度合成定理
上式对时间求导数,有
再对时间求导数,有
绝对加速度=相对加速度+牵连加速度
加速度合成定理
图1-16现象的解释
工程应用---汽车速度和里程测量
工程应用---绳拉船问题
§1-1 参考系 坐标系
1. 运动的绝对性
太阳表面的运动
太阳随银河系运动
地球自转
绝对静止的物体是没有的
为了确定一个物体的位置和描述一个物体的机
体组作参考,然后研究这一物体相对于选作参考的
参考系
物体的运动,这个被选作参考的物体称为
2. 运动描述的相对性
由于运动描述是相对的,描述物体的机械运动
车内观察者:落体运动
地面观察者:平抛运动
参考系不同,对它的运动的描述就不同
同一物体的运动,选取的
时,必须明确所用的参考系
要在参考系上选择一个固定的坐标系
常用坐标系:
就可以用它在此坐标系中的坐标来描述
O
x
z
y
参考系
A
P(x,y,z)
运动物体
3. 坐标系
为了定量地描述物体相对于参考系的
坐标系选定后,运动物体A 中任一点 P 的位置
平面直角坐标系、极坐标系和自然坐标系
运动物体
地面参考系
运动参考系
运动情况,
一、质点
一般情况下,运动物体的形状和大小都可能变化
将它视为一个具有质量而没有形状和大小的理想
太阳
地球
研究地球绕太阳的公转时,可将地球视为质点
作平动的刚性物体可视为质点
质心运动轨迹
但在某些问题中,可忽略物体的形状和大小,
物体——质点(理想模型)
§1-2 质点 质点运动的描述
时间和时刻
时刻
时间
运行时间
出发时刻 t1
到达时刻 t2
质点运动时,它经过的某一位置对应于某一时刻
质点所走过的某一段路程,对应于某一时间间隔
二、质点运动的描述 矢量法
如何确定质点的空间位置?
1.位置矢量 (位矢)
确定一参考点为坐标原点
连接原点与该质点作一矢量
的大小确定了质点和原点的距离,的方向确定了质点相对于原点的空间方位。
被称为位置矢量,简称位矢
因质点的空间位置是随着时间发生变化的
所以
任意时刻
质点的运动方程
找出质点的运动方程是质点运动学的
主要任务之一
2.位移
称为路程
3、速度
1. 平均速度
方向与 相同
2. 速度(瞬时速度)
?t 时间内平均速度
t 时刻位矢
t +?t 时刻位矢
?t 时间内位移
P
Q
t 时刻速度
方向为?t→0时 的极限方向,即 P 点的切线方向
平均速率
瞬时速率
4、加速度
1. 平均加速度
2. (瞬时)加速度
?t 时间内速度增量
t +?t 时刻速度
P
Q
t 时刻速度
方向与 相同
方向为?t→0时 的极限方向,总是指向曲线
凹的一侧
二 质点运动的描述 直角坐标法
1 位置矢量
*
方向:
大小:
分量式
从上式中消去参数 得质点的轨迹方程.
2 运动方程
P
3 位移
平面运动:
B
A
三维运动:
4 路程( )
从P1到P2:
路程
(3) 位移是矢量,路程是标量.
位移与路程的区别
(1) 两点间位移是唯一的.
(2) 一般情况 .
注意
的意义不同.
, ,
三 速度
1 平均速度
在 时间内,质点位移为
B
A
s
D
2 瞬时速度(简称速度)
若质点在三维空间中运动,其速度
1 平均加速度
B
与 同方向
反映速度大小和方向随时间变化快慢的物理量
四 加速度
A
2 (瞬时)加速度
加速度大小
加速度方向
曲线运动 指向凹侧
直线运动
说明:矢量性
瞬时性
相对性
一运动质点在某瞬时位于位矢 的端点处,其速度大小为
(A)
(B)
(C)
(D)
讨论
注意
例1-1 某质点沿x轴方向运动,位置与时间的关系为
(SI)。试求(1)第1秒内和第3秒内的
平均速度;(2)质点在第1秒末和第3秒末的速度
和加速度。
解
(1)
时,
;
时,
则第1秒内的位移
第1秒内的平均速度大小为
方向沿x轴正向
(SI)。试求(1)第1秒内和第3秒内的
平均速度;(2)质点在第1秒末和第3秒末的速度
和加速度。
第3秒内的平均速度大小为
解
方向沿x轴负向
(1)
(2)
第1秒末的速度大小
第3秒末的速度大小
方向沿x轴负向
方向沿x轴负向
(2)
求导
求导
积分
积分
质点运动学两类基本问题
一 由质点的运动方程可以求得质点在任一时刻的位矢、速度和加速度;
二 已知质点的加速度以及初始速度和初始位置, 可求质点速度及其运动方程.
四 质点运动的描述 自然法
曲线运动
圆周运动
(1)匀速率圆周运动 向心加速度
?t 时间内速度增量为
A
B
t 时刻速度
t +?t 时刻速度
?t 时间内速度增量
加速度为
当 时加速度大小为
方向沿半径指向圆心,称为向心(法向)加速度
圆周运动
(2)变速圆周运动 切向加速度和法向加速度
速度增量分解为
速度增量的分解
A
B
t 时刻速度
t +?t 时刻速度
?t 时间内速度增量
瞬时加速度为
法向加速度
方向 沿半径指向圆心
大小
切向加速度
方向 与瞬时速度方向平行
大小
反映速度方向改变
反映速度大小变化
总加速度
与瞬时速度方向之间的夹角
大小
?
2、一般曲线运动 自然法
以轨道上任一点O为参考点,质点所在的位置P点到
O点的轨道长度s称为自然坐标
1,自然坐标s是标量
2,s可正可负
(1)自然坐标系 自然坐标
(2)速度在自然坐标系下的表示
质点在 P 点附近轨道弧元上的运动可视为在
法向加速度
切向加速度
曲率圆
总加速度
切向加速度大小
法向加速度大小
曲线于 P 点的曲率半径
t
a
曲率圆上的运动。
(3)加速度在自然坐标系下的表示
指向曲线凹的一侧
方向由 的数值决定
方向一致
方向相反
例题1-6 物体被抛出后到达 P点时,速度 与
解 不考虑空气阻力,物体的总加速度为
始终垂直于速度方向并指向抛物线凹的一侧
与速度方向相同
若 P 点位于最高点的右边,
若P 点位于最高点的左边,
与速度方向相反
P点的曲率半径,并给出曲率半径最小值。
时的切向加速度、法向加速度;(2)运动轨道在
水平方向成q 角,若忽略空气阻力,求物体在 P点
方向竖直向下
结果表明,斜抛物体达到最高点时, ,其切向
可得 P 点的曲率半径
P
O x
y
得切向加速度和法向速度的大小分别为
加速度为零,法向加速度有最大值,而轨道曲率半
径达到最小值
一 经典力学时空观
§1-3 相对运动
地面上的人测得
车上的人测得
经典力学时空观认为:
、
不依赖与观察者所在的参考系
时间和长度的绝对性是经典力学或牛顿力学的基础.
实际上时间和空间的测量是依赖于参考系的相对运动速度,但速度远小于光速时,测量结果的差异可以忽略。
经典力学时空观
时间和长度是绝对的
位矢、位移、速度、
加速度、运动轨迹都
是相对的
物体运动的轨迹依赖于观察者所处的参考系
二、相对运动
运动物体的位矢、速度、加速度、运动轨迹是相对
于某一参考系而言的,不同的参考系(观测者)因
本身的运动状态,对同一质点的测量结果可能不一样。
物体运动的轨迹依赖于观察者所处的参考系
本身的运
运动参考系 S'
静止参考系 S
由矢量加法原理有
运动质点在两参考系中位矢间的关系
运动质点
P
静止参考系 S
运动参考系 S'
速度和加速度合成定理
绝对速度=相对速度+牵连速度
速度合成定理
上式对时间求导数,有
再对时间求导数,有
绝对加速度=相对加速度+牵连加速度
加速度合成定理
图1-16现象的解释
工程应用---汽车速度和里程测量
工程应用---绳拉船问题
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
