必修1 第一章 第1讲 运动的描述 本章综合与测试课件21张PPT (2)
文档属性
| 名称 | 必修1 第一章 第1讲 运动的描述 本章综合与测试课件21张PPT (2) |  | |
| 格式 | ppt | ||
| 文件大小 | 586.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-09-28 14:45:19 | ||
图片预览





文档简介
相遇和追及问题
一、 相遇和追及
当两个物体在同一条直线上运动时,由于两个物体的运动情况不同,因此两个物体间的距离不断发生变化。相向而行会发生相遇;同向行驶过程中,两物体的间距越来越大或者越来越小,这时就会涉及追及,相遇或避免碰撞问题。
思考:在直线运动中,为什么会出现相遇和追及情况呢?
二、处理方法:
化繁为简,归类总结
1.相遇问题:
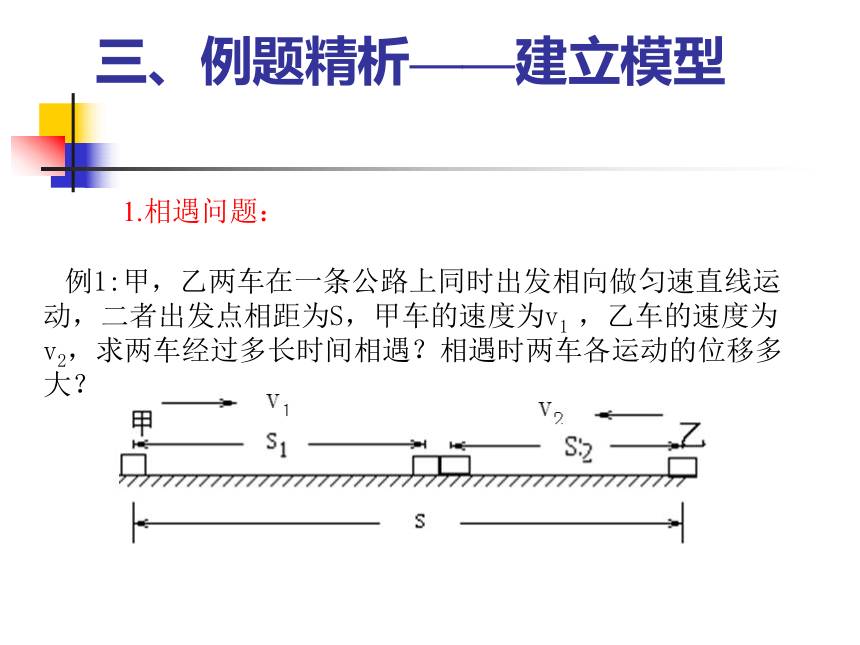
三、例题精析——建立模型
例1:甲,乙两车在一条公路上同时出发相向做匀速直线运动,二者出发点相距为S,甲车的速度为v1 ,乙车的速度为v2,求两车经过多长时间相遇?相遇时两车各运动的位移多大?
设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1+s2=s ②
对甲: s1= v1 t1 ③
对乙: s2= v2 t2 ④
代①③④入②:得 t=
其中:甲位移 s1=
乙位移:s2=
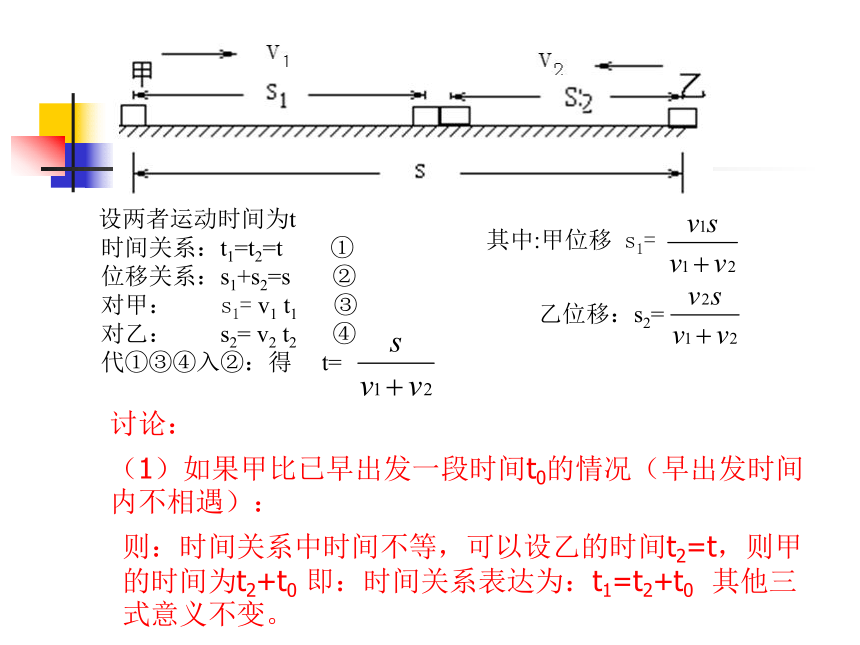
讨论:
(1)如果甲比已早出发一段时间t0的情况(早出发时间 内不相遇):
则:时间关系中时间不等,可以设乙的时间t2=t,则甲的时间为t2+t0 即:时间关系表达为:t1=t2+t0 其他三式意义不变。
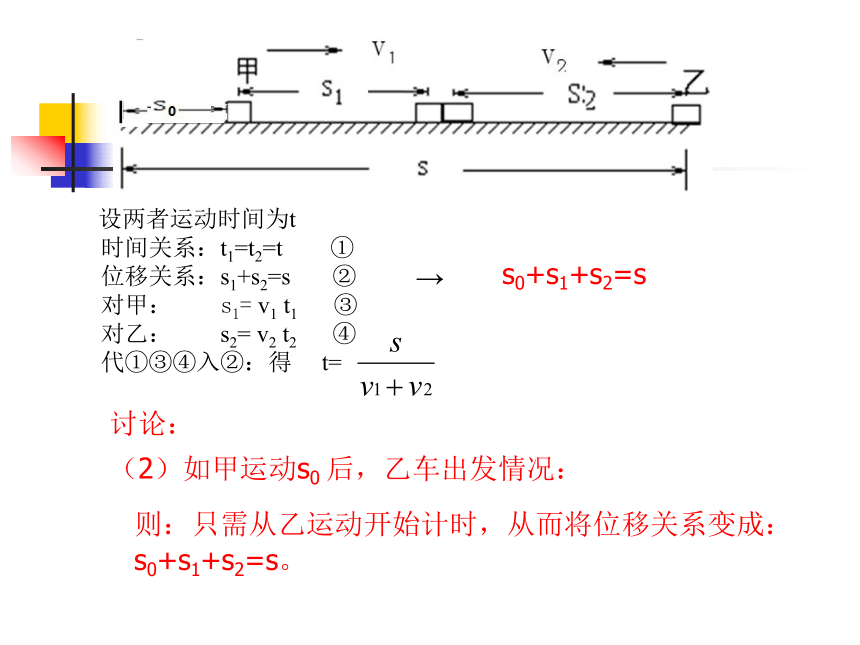
(2)如甲运动s0 后,乙车出发情况:
设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1+s2=s ②
对甲: s1= v1 t1 ③
对乙: s2= v2 t2 ④
代①③④入②:得 t=
讨论:
则:只需从乙运动开始计时,从而将位移关系变成:s0+s1+s2=s。
s0+s1+s2=s
→
设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1+s2=s ②
对甲: s1= v1 t1 ③
对乙: s2= v2 t2 ④
代①③④入②:得 t=
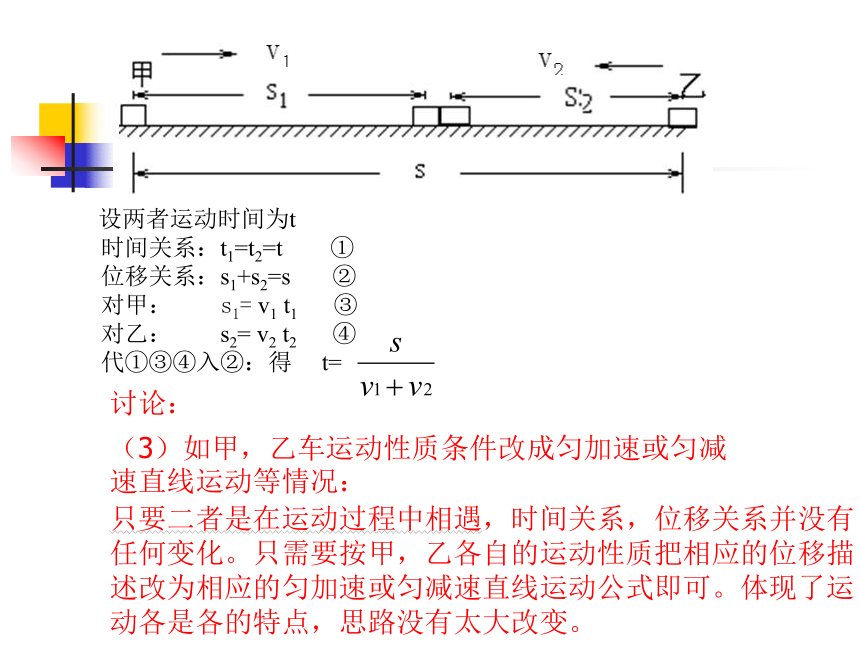
讨论:
(3)如甲,乙车运动性质条件改成匀加速或匀减速直线运动等情况:
只要二者是在运动过程中相遇,时间关系,位移关系并没有任何变化。只需要按甲,乙各自的运动性质把相应的位移描述改为相应的匀加速或匀减速直线运动公式即可。体现了运动各是各的特点,思路没有太大改变。
1.认真审题,画出物体的运动情境草图
2.建立模型。从“时间关系,位移关系,运动各描述各 。”入手分析。
3.列方程求解,验证答案的合理性
归类总结
在直线运动中,由相遇问题得到的模型,在同向追及情况下是不是也可以适用呢?
思考:
例2:甲车以10m/s的速度在平直的公路上匀速行驶,经过乙车旁边时,乙车同时从静止开始做a=2m/s2匀加速直线运动,求:(1)经过多长时间两车再次相遇?运动的位移各是多大?(2)在追上之前的过程中,两车的最大间距△S是多少?
2.追及问题:
认真审题,画出物体的运动情境草图:
(1)设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1=s2 ②
对甲: s1= v1 t1 ③
对乙: s2=
at22 ④
代数据①③④入②: 得:t=10s s1= s2=100m
(1)设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1=s2 ②
对甲: s1= v1 t1 ③
对乙: s2=
at22 ④
讨论:
(1)在同地,同向条件下,如甲比已早出发一段时间t0 的情况:
则:时间关系中时间不等,可以设乙的时间t2=t,则甲的时间为t2+t0 即:时间关系表达为:t1=t2+t0 其他三式意义不变。
建立模型适用
(1)设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1=s2 ②
对甲: s1= v1 t1 ③
对乙: s2=
at22 ④
(2)在同时,同向的条件下,如甲比乙先出发s0情况:
讨论:
则:只需从乙运动开始计时,从而将位移关系变成:s0+s1=s2
建立模型适用
(1)设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1=s2 ②
对甲: s1= v1 t1 ③
对乙: s2=
at22 ④
讨论:
(3)在同时,同地,同向的条件下,如甲车运动性质条件改成匀加速或匀减速直线运动等情况:(能追上)
只要二者是在运动过程中相遇,时间关系,位移关系并没有任何变化。只需要按甲的运动性质把相应的位移描述改为相应的匀加速或匀减速直线运动公式即可。体现了运动各是各的特点,思路没有太大改变。
建立模型适用
(2)在追上之前的过程中,两车的最大间距△S是多少?
讨论:
当v甲>v乙 即(v1>v2):
当v甲<v乙 即(v1<v2):
当v甲=v乙 即(v1=v2):
根据上述分析:可见速度相等时,两车间距最大。——临界距离
甲比乙慢,乙追甲,间距变小;
甲比乙快,甲在前,间距变大;
甲已一样快,间距最大。(如上图)
关键:由临界条件求解时间
速度相等——经常是两物体追及过程中的临界条件,即:距离最大、最小、恰好相撞,恰好避免相撞等,往往成为解题模型的关键条件。
特别注意:
1.认真审题,画出物体的运动情境草图
2.建立分析模型。总结口决:“时间关系,位移关系,运动各描述各,临界条件出现在速度相等时。”
3.列方程求解,验证答案的合理性
五、解题思路总结:
例题3:火车A以速度v1匀速行驶,司机发现正前方
同一轨道上相距s处有另一火车B沿同方向以速度v2
做匀速运动(对地,v2〈v1. ),A车司机立即以加
速度(绝对值)a紧急刹车,为使两车不相撞,a应
满足什么条件?
六、课后演练:
一、 相遇和追及
当两个物体在同一条直线上运动时,由于两个物体的运动情况不同,因此两个物体间的距离不断发生变化。相向而行会发生相遇;同向行驶过程中,两物体的间距越来越大或者越来越小,这时就会涉及追及,相遇或避免碰撞问题。
思考:在直线运动中,为什么会出现相遇和追及情况呢?
二、处理方法:
化繁为简,归类总结
1.相遇问题:
三、例题精析——建立模型
例1:甲,乙两车在一条公路上同时出发相向做匀速直线运动,二者出发点相距为S,甲车的速度为v1 ,乙车的速度为v2,求两车经过多长时间相遇?相遇时两车各运动的位移多大?
设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1+s2=s ②
对甲: s1= v1 t1 ③
对乙: s2= v2 t2 ④
代①③④入②:得 t=
其中:甲位移 s1=
乙位移:s2=
讨论:
(1)如果甲比已早出发一段时间t0的情况(早出发时间 内不相遇):
则:时间关系中时间不等,可以设乙的时间t2=t,则甲的时间为t2+t0 即:时间关系表达为:t1=t2+t0 其他三式意义不变。
(2)如甲运动s0 后,乙车出发情况:
设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1+s2=s ②
对甲: s1= v1 t1 ③
对乙: s2= v2 t2 ④
代①③④入②:得 t=
讨论:
则:只需从乙运动开始计时,从而将位移关系变成:s0+s1+s2=s。
s0+s1+s2=s
→
设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1+s2=s ②
对甲: s1= v1 t1 ③
对乙: s2= v2 t2 ④
代①③④入②:得 t=
讨论:
(3)如甲,乙车运动性质条件改成匀加速或匀减速直线运动等情况:
只要二者是在运动过程中相遇,时间关系,位移关系并没有任何变化。只需要按甲,乙各自的运动性质把相应的位移描述改为相应的匀加速或匀减速直线运动公式即可。体现了运动各是各的特点,思路没有太大改变。
1.认真审题,画出物体的运动情境草图
2.建立模型。从“时间关系,位移关系,运动各描述各 。”入手分析。
3.列方程求解,验证答案的合理性
归类总结
在直线运动中,由相遇问题得到的模型,在同向追及情况下是不是也可以适用呢?
思考:
例2:甲车以10m/s的速度在平直的公路上匀速行驶,经过乙车旁边时,乙车同时从静止开始做a=2m/s2匀加速直线运动,求:(1)经过多长时间两车再次相遇?运动的位移各是多大?(2)在追上之前的过程中,两车的最大间距△S是多少?
2.追及问题:
认真审题,画出物体的运动情境草图:
(1)设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1=s2 ②
对甲: s1= v1 t1 ③
对乙: s2=
at22 ④
代数据①③④入②: 得:t=10s s1= s2=100m
(1)设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1=s2 ②
对甲: s1= v1 t1 ③
对乙: s2=
at22 ④
讨论:
(1)在同地,同向条件下,如甲比已早出发一段时间t0 的情况:
则:时间关系中时间不等,可以设乙的时间t2=t,则甲的时间为t2+t0 即:时间关系表达为:t1=t2+t0 其他三式意义不变。
建立模型适用
(1)设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1=s2 ②
对甲: s1= v1 t1 ③
对乙: s2=
at22 ④
(2)在同时,同向的条件下,如甲比乙先出发s0情况:
讨论:
则:只需从乙运动开始计时,从而将位移关系变成:s0+s1=s2
建立模型适用
(1)设两者运动时间为t
时间关系:t1=t2=t ①
位移关系:s1=s2 ②
对甲: s1= v1 t1 ③
对乙: s2=
at22 ④
讨论:
(3)在同时,同地,同向的条件下,如甲车运动性质条件改成匀加速或匀减速直线运动等情况:(能追上)
只要二者是在运动过程中相遇,时间关系,位移关系并没有任何变化。只需要按甲的运动性质把相应的位移描述改为相应的匀加速或匀减速直线运动公式即可。体现了运动各是各的特点,思路没有太大改变。
建立模型适用
(2)在追上之前的过程中,两车的最大间距△S是多少?
讨论:
当v甲>v乙 即(v1>v2):
当v甲<v乙 即(v1<v2):
当v甲=v乙 即(v1=v2):
根据上述分析:可见速度相等时,两车间距最大。——临界距离
甲比乙慢,乙追甲,间距变小;
甲比乙快,甲在前,间距变大;
甲已一样快,间距最大。(如上图)
关键:由临界条件求解时间
速度相等——经常是两物体追及过程中的临界条件,即:距离最大、最小、恰好相撞,恰好避免相撞等,往往成为解题模型的关键条件。
特别注意:
1.认真审题,画出物体的运动情境草图
2.建立分析模型。总结口决:“时间关系,位移关系,运动各描述各,临界条件出现在速度相等时。”
3.列方程求解,验证答案的合理性
五、解题思路总结:
例题3:火车A以速度v1匀速行驶,司机发现正前方
同一轨道上相距s处有另一火车B沿同方向以速度v2
做匀速运动(对地,v2〈v1. ),A车司机立即以加
速度(绝对值)a紧急刹车,为使两车不相撞,a应
满足什么条件?
六、课后演练:
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
